基于概率理论的弹簧消隙齿轮受信仪空程误差分析∗

（92941部队41分队 葫芦岛 125001）

1 引言

伺服系统中受信仪的齿轮传动系统属于小模数齿轮传动，其空程误差是小模数齿轮传动设计的核心指标，是影响伺服精度和系统稳定性的决定性因素［1］。由于影响空程误差的因素较多（如温度、机械加工、安装等），要在一定的条件下使得受信仪的空程误差满足系统指标，就要采用一些特殊的措施来调节控制空程误差的数值，从而来满足受信仪的精度要求。目前使用最为广泛的是采用弹簧消隙齿轮机构。这种消隙机构从原理上消除了由齿轮本身制造误差引起的几乎所有的齿隙误差［2］，因此被大量的应用于数据传动机构中。但是，在实际的应用中，弹簧消隙齿轮机构中的空程误差并不能被完全消除，对受信仪的精度产生一定程度的影响。本文以某型受信仪的弹簧消隙齿轮机构为分析模型，考虑到弹簧消隙、弹性变形等因素的影响，引入概率统计的理论，建立一种符合实际、经济可靠的弹簧消隙齿轮空程误差的计算方法。

2 概率统计理论的引入

目前关于弹簧消隙小模数齿轮传动机构的空程误差计算，仍普遍采用将各种因素极值相加来计算最大空程误差的数值，但这种情况只是在各影响因素处于极限值时才出现，事实上，各影响因素很少可能会同时处于最大值和同一相位。所以用极值法得到的数值，对绝大多数设计来说是不切实际偏大的数值，从而不合理地提高了制造精度，导致不经济的后果。由此可以看出，行业内对弹簧消隙齿轮传动链空程误差的系统认识还有一定偏差［3］，尚没有一种完善、可靠的统计方法可供参考。

本文在分析弹簧消隙齿轮受信仪空程误差时，引入了概率统计理论，认为齿轮误差及其它误差都是连续型随机变量，各项误差源的分布都是相互独立的，遵循正态分布或其他简单的典型分布规律［4］。通过分析各环节随机误差分布情况，忽略影响很小的轴系误差，运用合理的统计方法，推导出弹簧消隙齿轮受信仪空程误差的数学计算式，以此得到较为经济可靠的设计。

3 消隙齿轮传动机构空程误差分析

影响消隙齿轮传动机构空程误差的因素主要有：齿轮齿厚减薄量、齿轮副中心距误差、齿轮的几何偏心、齿形误差、轴承的径向游隙、轴承内外圈的径向偏摆、温度变化和弹性变形［5～6］。

3.1 弹簧加载消隙齿轮对空程误差影响分析

弹簧加载消隙齿轮是利用弹簧的弹力来调节双片齿轮的齿厚，从而达到控制空程误差的目的。如图1所示，该弹簧加载消隙齿轮是由固定齿轮和浮动齿轮组成：固定齿轮被固定在传动轴上，浮动齿轮空套在固定齿轮上，两片齿轮之间由加载弹簧连接。

弹簧加载齿轮传动的消隙原理在于：当双片齿轮与配偶齿轮啮合时，弹簧将迫使浮动齿轮相对于固定齿轮作微量转动，而使齿轮副获得紧密的双面啮合，利用弹簧力消除了啮合齿非工作面间的间隙，从而达到减小空程误差的目的。因此，只要控制好加载弹簧的弹性力矩，使得弹性力矩大于负载力矩，双片齿轮就能够消除由齿轮本身制造引起的全部齿隙，从而有效地消除空程误差，并且与齿轮本身的精度几乎无关。但弹性力矩也不宜过大，否则导致齿面磨损加剧。纵上所述，齿轮的加工误差，包括齿轮齿厚减薄量、齿轮副中心距误差、齿轮的几何偏心、齿形误差等因素对消隙齿轮传动机构空程误差的影响可以不予考虑。

3.2 轴承径向间隙对空程误差影响分析

由于轴承径向间隙属于随机误差，因此根据工程设计经验，在分析轴承径向间隙对齿轮传动精度的影响时，一般认为轴承径向间隙∆S应服从正态分布［7～8］，如图2所示。

图2 ∆S概率分布图

式中，μS为由径向间隙引起的齿轮副圆周侧隙的均值，μm；∆S为径向间隙误差，μm；∆Sm为径向间隙误差的平均值，μm；∆Ss、∆Si为径向间隙误差的上偏差和下偏差，μm；αn为法向压力角，度；β为螺旋角，度；βb为基圆螺旋角，度。

空程误差是当主动轮逆转时从动轮所滞后的转角，此转角在主动轮逆转中表现出来。因此，在主动轮上所表现出来的由轴承径向间隙引起的空程误差∆φS为

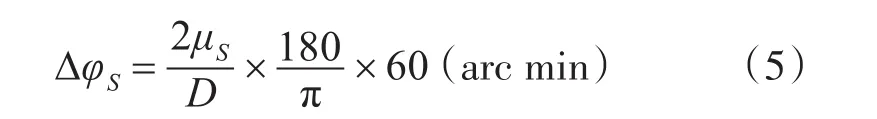
式中，D为主动轮的分度圆直径，mm。

3.3 环境温度对空程误差影响分析

在温度变化条件下，运转的齿轮的啮合要尺寸变化的影响，如果齿轮、轴和箱体都用同一材料制成，就没有很大的侧隙变化。但是，假如这三者的材料的膨胀系数不相同，则在温度变化大的条件下，对侧隙的影响是很大的。因此，要考虑到温度的影响并设计出在恶劣条件下运转时能避免干涉的齿轮啮合，而且要考虑在其他在极端的温度条件下扩大了的侧隙值。为保证齿轮副正常传动，应考虑热变形所引起的侧隙变化量。

由环境温度变化引起的圆周侧隙jtT可用下式来计算：

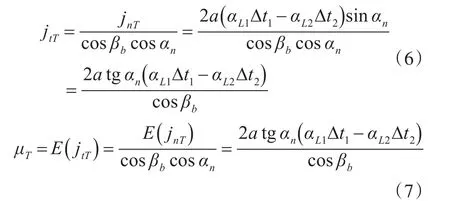
式中：μT为由环境温度变化引起的齿轮副圆周侧隙的均值，μm；a为齿轮副的中心距，mm；αL1、αL2为齿轮和箱体材料的线膨胀系数，/10ˆ6℃；∆t1、∆t2为齿轮和箱体与标准温度( )20℃ 的温度之差，℃。

若计算结果为正值，表示齿轮的热胀量大于箱体的热胀量，迫使侧隙减小。如果齿轮副预留的侧隙过小，则有可能使齿轮卡死。若计算结果为负值，情况便与此相反，表示侧隙增大。

则在主动轮上所表现出来的由环境温度引起的空程误差为

式中，D为主动轮的分度圆直径，mm。

3.4 弹性变形对齿轮副侧隙的影响

材料的弹性是侧隙的另一个来源。所有材料在载荷作用下都会挠曲，其变化量与弹性模数和几何尺寸成比例。除了轮齿的挠曲外，还应该考虑轴的挠曲等。在齿轮传动机构工作过程中，啮合力的变化将使轴发生扭转和弯曲，从而使轮齿发生弯曲变形等，当反向回转时，这些因素都将影响齿轮传动机构的空程误差［9～10］。

将齿轮轴转化为简支梁力学模型，如图3所示。

图3 弹性变形示意图

在啮合力方向上的挠度f为

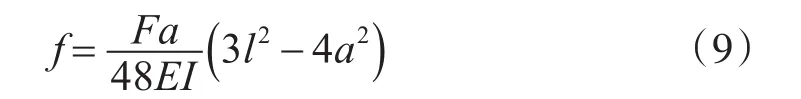
式中，F为齿轮啮合力，N；E为轴材料的弹性模量，MPa；I为轴材料的截面惯性矩，mm4；l为齿轮轴两端支撑点距离，mm；a为齿轮啮合点距齿轮轴一端支撑点的距离，mm。

则弹性变形引起的圆周侧隙jtf为

式中：μf为由弹性变形引起的齿轮副圆周侧隙的均值，μm。

则在主动轮上所表现出来的由弹性变形引起的空程误差∆φf为

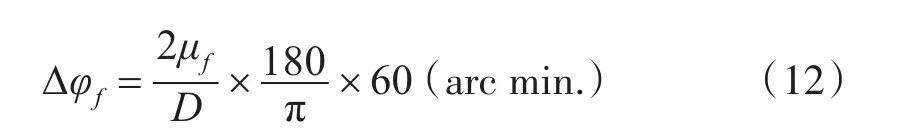
式中，D为主动轮的分度圆直径，mm。

环境温度变化引起的尺寸变化、弹性变形等所带来的侧隙不是直接从几何设计尺寸中表示出来，而只能从对温度范围和动态力的实际情况的分析计算中推断出来。

4 单级消隙齿轮机构空程误差分析

单级消隙齿轮机构的圆周侧隙为

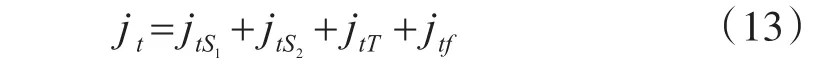
式（13）中分别考虑了轴承径向间隙、环境温度的变化以及弹性变形对消隙齿轮机构空程误差的影响。

敏感报告（S）表示，如果抗菌药在感染部位达到通常可达到的浓度，则该抗菌药可能抑制病原菌的生长。中介报告（I）表示，结果应该被认为是模棱两可，如果微生物对替代的，临床上可用的药物不完全敏感，则应重复测试。这一类别意味着，在药物生理浓缩的身体部位，或在药物可使用的高剂量情况下，临床可能适用。这一类别还提供了一个缓冲区，防止小的、没有控制的技术因素，造成解释的重大差异。耐药报告（R）表示，如果抗菌药在感染部位达到通常可达到的浓度，该抗菌药不太可能抑制病原菌的生长；应该选择其他治疗方法。

由于各项因素相互独立，因此采用各项空程误差迭加统计，这也是最安全的估计方法［11］。由此可得：

在主动轮上所表现出来的单级消隙齿轮机构的空程误差∆φ为

5 多级消隙齿轮传动系统空程误差统计分析

以n级消隙齿轮传动系统为例，如图4所示，I为输入轴，O为输出轴。

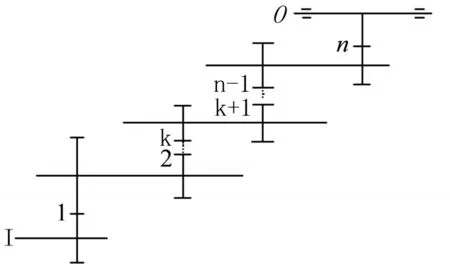
图4 n级消隙齿轮传动系统

则n级消隙齿轮传动系统的空程误差如式（16）所示：

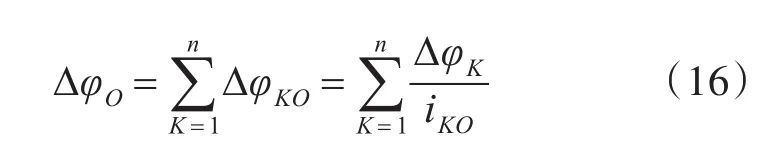
式中，∆φO为系统的空程误差，arc min.；∆φK为以主动轮空程误差表示的第K级消隙齿轮机构的空程误差，arc min.；iKO为从第K级消隙齿轮机构的主动轮到输出轴O的传动比。

则输出轴O上的空程误差为

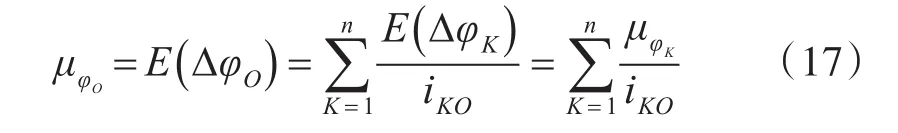
式中，μφK为第K级消隙齿轮机构在小齿轮上的空程误差，arc min。

6 某型弹簧消隙齿轮受信仪空程误差计算例

设计条件如下：

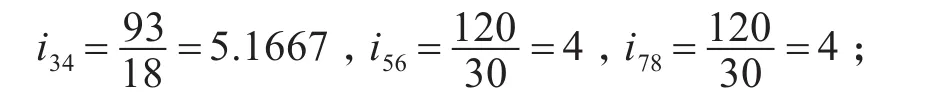
2）从输入轴到精自整角机的传动比为

i12×i34=3.6176×5.1667=18.6912；

从精自整角机到粗自整角机的传动比为

i56×i78=4×4=16；

从输入轴到粗自整角机的传动比为：

i12×i34×i56×i78=3.6176×5.1667×4×4=299.0588；

3）轴承选用深沟球轴承，0组游隙，其径向游隙2μm ～13μm ；

4）齿轮2、4、6、8采用双片齿轮弹簧消隙结构；

5）粗自整角机的精度为10′，精自整角机的精度为 3′；

6）齿轮及齿轮轴采用45＃钢，壳体采用普通碳钢。

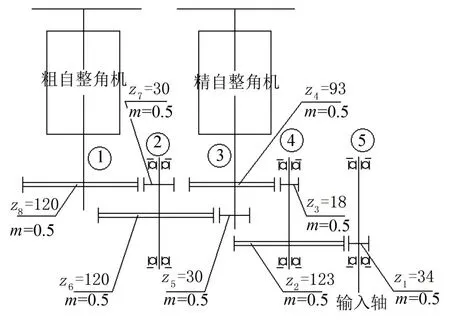
图5 某型弹簧消隙齿轮受信仪传动系统示意图

受信仪的精度以输入轴到精自整角机所产生的空程误差为主要衡量标准。按本文介绍的统计方法进行计算，所得到的结果是：

1）由输入轴到粗自整角机所产生的空程误差（折算到齿轮8上）为1.24′，小于粗自整角机的精度10′，且数值较小，满足设计要求；

2）由输入轴到精自整角机所产生的空程误差（折算到齿轮4上）为1.52′，小于精自整角机的精度 3′。

经批次检验，该型弹簧消隙齿轮受信仪传动系统输入轴到精自整角机的空程误差（折算到齿轮4上）为 0.78′～0.92′，因此，本文介绍的计算方法是经济可靠的，按此方法计算而得的空程误差的数值满足设计要求。

7 结语

通过上述分析计算可以看出，本文在对某型弹簧消隙齿轮受信仪传动系统空程误差的分析过程中，引入了概率统计的概念，避免了因传统算法而导致的不合理的公差要求，可靠地满足了系统性能指标，较为客观地反映了弹簧消隙齿轮传动系统空程误差的真实情况，后期可以通过增大轴径设计、减少装配偏心以及提高弹簧加载力矩等措施进一步减少受信仪的空程误差。通过本文的相关论述，使弹簧消隙齿轮传动系统空程误差的分析有一个比较具体的理论依据，减少了设计盲目性和难度，指明了改进方向，对以后的工程设计具有一定的指导意义［12］。