基于六维力传感器的机器人末端执行器碰撞位置检测方法

李倩倩，袁宏祥，马 昕，宋 锐

(山东大学 控制科学与工程学院，山东 济南 250061)

1 问题的描述

力觉感知是智能机器人与外界环境交互的一项重要功能，特别是对于抓取[1,2]、轮廓检测[3]、避障[4]、人机交互[5-6]以及力反馈控制[7]等操作尤为重要。因此，力传感器(特别是六维力/力矩传感器)被越来越多地集成到机器人系统中[8-9]。例如：在工业机器人生产线中，力传感器被用来做碰撞检测和反馈控制[10]；在机械灵巧手系统中，力传感器被用来实现触觉感知；在手术机器人系统中，力传感器被用来辅助安全控制和碰撞检测等[11-12]。可见，碰撞检测和反馈控制是力觉感知的两个关键功能[13-14]。而碰撞位置检测则是碰撞检测的重要内容之一。

在传感器和机器人技术的发展过程中，基于力/力矩传感器的碰撞位置检测方法已经有很多研究。最早的可追溯到的为文献[15]中提到的：1989年，Tsujimura等基于力/力矩传感器和一个结构化的探针建立了一种物体轮廓探测方法;1990年，Bicchig等[1]从力学的角度对碰撞感知进行了分析，在文章中阐述了碰撞感知的基础理论，并提出了基于几种常见形状的结构化探针的位置感知解决方案;1992年，Kazanzides等[16]在文献中提到了一种在外科手术机器人系统中，通过线性回归方法监测碰撞点的方法，但文章中没有给出计算过程;1996年，周学才等[17-18]提出一种与文献[13]类似的方法，用于实现机械手系统中的指端碰撞位置感知，但与文献[15]不同，这类方法采用了矩阵理论的方法，并且加入了重力校准，为实际应用打下了良好基础;2004年，韩壮志等[19-20]也提出一种基于力/力矩传感器数据和机械手指端几何模型求解触点位置的方法;2015年，Leng等[21-22]通过安装在六自由度机械臂腕部的力传感器实现了机器人末端工具的碰撞位置检测，并基于机械臂的运动学模型建立了重力补偿和动态补偿方法。此外，文献[23]和文献[24]中也同样分析了碰撞过程的几何约束和自然约束，并基于六自由度机械臂的运动学模型给出了重力和动态补偿方法。

基于力学数据求解碰撞位置的难点在于多解问题，因此必须引入额外的约束条件来求解。总结上文中提到的研究方法，无一例外的依靠几何约束条件来求解，因此要求碰撞物体必须为形状规则或者可几何建模(如长度一定的探针、球形、平面等)，并且要求碰撞表面光滑且不能变形，对实际应用条件要求苛刻。然而，现实生活中的碰撞大多数发生在非结构化的环境中，且往往会出现变形。因此，上述基于碰撞表面几何约束的方法都无法被应用。根据碰撞表面的触点数量的不同，可以将实际生活中的碰撞分为3种：单触点碰撞、平面或表面均匀接触碰撞、多触点碰撞，如图1右侧第一行所示。而单触点碰撞又可以分为结构化环境下(可建模预测)碰撞和非结构化环境下的碰撞，如图1右侧第二行所示。除此之外，形变也是碰撞过程中经常遇到的一种情况，如图1右侧f所示。事实上，表面均匀接触的碰撞和多触点碰撞都可以看作是单触点碰撞的特殊组合形式，因此本文重点针对非结构化环境下的单触点碰撞及形变问题进行了分析。

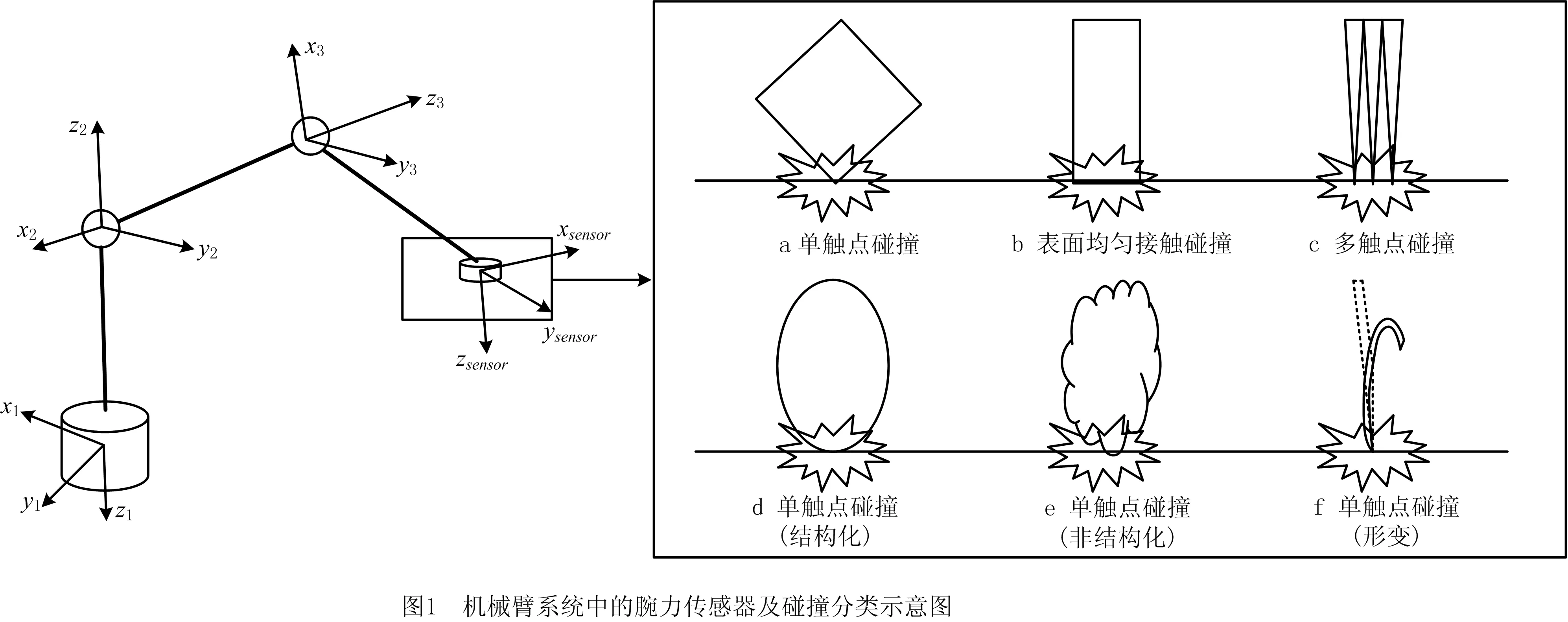
为了克服基于几何约束方法的局限性，摆脱触点位置检测对碰撞物体形状信息的依赖，本文基于机械臂腕力传感器建立了一种仅依靠力学数据触点位置检测方法。该方法将碰撞视为一个连续的过程，通过碰撞过程中时间轴上的多组力/力矩采样数据互为约束条件来计算触点的位置，并建立了最小误差法搜索策略，在多组结果中搜索出最优的解。因此，所提检测方法既可以应用于结构化的环境，也可以应用于非结构化和形变的环境，有效地推进了力觉感知在机器人系统中的应用，同时也为多触点检测奠定了基础。

2 碰撞定位模型

以图1左侧的机械臂系统为例，设最终检测到的触点位置为RP，根据机械臂的运动学模型可以得到：

(1)

式中SP为触点在力传感器坐标系中的位置。因此，对于整个机器人系统来说，首先应该标定传感器在系统中的位置，之后触点检测问题可简化为在传感器坐标系中求解触点位置。

2.1 基于几何约束的碰撞定位模型

根据六维力传感器的数据格式，碰撞力和力矩均可以被分解为3个坐标轴上的分量。因此，设碰撞力和力矩分别为F(Fx,Fy,Fz)，M(Mx,My,Mz)，则两者与触点位置的关系可表示为：

M(Mx,My,Mz)=L(x,y,z)×F(Fx,Fy,Fz)。

(2)

式中L为坐标原点到触点的向量。式(2)用矩阵形式可表达为：

(3)

{P(x,y,z)|(x,y,z)∈L×F=

M∩S(x,y,z)=0}。

(4)

在这些几何约束方法中，触点检测往往只能采用球形、圆柱或者其他容易描述的结构体作为探针，因此极大的限制了应用范围。此外，由于传感器数据采集过程中的噪声和碰撞过程中的变形等，导致该类方法的鲁棒性极差，使其难以在实际应用中发挥作用。

2.2 动态力学数据自约束模型

事实上，当F(Fx,Fy,Fz)与M(Mx,My,Mz)为常数时，式(3)的解集{P}分布在一条空间直线上。这条空间曲线通常被称为外力矢量线，本文将其定义为Lc(P)，参数形式可表达为：

(5)

显然F(Fx,Fy,Fz)为直线的方向向量。因此，不同的碰撞力决定了不同方向的外力矢量线。通常情况下，由于碰撞物体的运动方向与碰撞力方向不同，就会导致不同时刻的两组外力矢量线不平行(相交)，且交点即为碰撞接触点。综上所述，触点位置可以通过求解两组外力矢量线的交点来得到：

{P(x,y,z)|(x,y,z)∈Lc1(p)∩Lc2(p)}。

(6)

3 基于自约束模型的碰撞位置检测方法

3.1 数据预处理

文献[1]中对碰撞力已经进行了详细分析，并将碰撞过程中触点所受的外力分解为垂直于碰撞表面的压力和与碰撞表面相切的摩擦力。而在将碰撞过程看作一个动态过程来求解触点位置时，碰撞外力可以不用分解。此外，力传感器的检测到的力除了碰撞外力Fcontact，还包括一个内力Finter和一个动态力Fdynamic，即

Fsensor=Fcontact+Finter+Fdynamic。

(7)

式中的内力主要来自于工具和力传感器装配过程中产生的挤压力，通常在装配完成后就可视为定值。动态力则来自于末端工具的重力，会随着机械臂姿态的变化而变化。如此一来，由碰撞产生的外力可以通过以下公式来计算：

Fcontact=Fsensor-Finter-FgravityRg→s。

(8)

式中：Fgravity为末端工具在大地坐标系中的重力;Rg→s为大地坐标系到力传感器坐标系的转换矩阵。

此外，基于几何约束的方法一般要通过重力补偿和动态补偿来将碰撞外力从传感器采集到的数据中分离出来。但从碰撞过程(从接触到发生位移)的角度，随时间变化的只有碰撞力。因此，本文只将碰撞产生的外力视为外力，其他力均视为内力。同时，将碰撞从一个即刻的状态扩展到一个时间轴上的过程，也意味着可以获取到多组传感器数据，建立时间函数：

Fcontact(t)=Fsensor(t)-Finter-FgravityRg→s。

(9)

对式(9)求导可得：

ΔFcontact=ΔFsensor。

(10)

显然ΔFcontact也同样适用于式(2)。因此，采用碰撞力的导数，即传感器两帧之间的差值作为式(2)的输入量。

3.2 基于投影法的外力矢量线交点求解

(11)

图2b给出了两条外力矢量线在某个坐标平面上的投影。如图2所示，两条外力矢量线虽然在三维空间中的可探测范围内不相交，但是其在坐标平面上投影线的交点却会落在真实触点投影的附近。因此，可以先通过投影交点求得触点在3个坐标平面的投影点坐标，然后结合原始的外力矢量线方程求得触点的三维坐标值，如图3所示。

(12)

其中σ为一个判定因子，用于从三个坐标平面中选择一个最优的作为投影平面，其具体规则为：

(13)

(14)

假设最终选定的投影平面为XOY，则P1(x,y,z1)和P2(x,y,z2)的解算公式为：

(15)

和

(16)

3.3 最小误差搜索策略

为进一步缩小误差，提高触点位置检测的鲁棒性，本文采用在碰撞过程的多组数据中搜索最优解的方法。假设碰撞过程的多组力传感器数据产生的外力矢量线如图4a所示，则利用两组相邻数据通过投影法求得的触点集如图4b所示，其中表示真实的触点位置，为通过最小误差法搜索出的最优解。最小误差法的原理为：

设最终的触点位置检测结果为P″(x″,y″,z″)，则通过式(3)可得：

(17)

其中δ(δMx,δMy,δMz)表示误差，其定义为：

(18)

最终，改进的触点位置检测方法可以归纳为如图5所示的流程。

4 实验结果及分析

本文分别通过一组随机点检测实验和一组形变实验验证了改进的触点位置检测方法的精度和有效性。其中，随机点实验将改进方法的精度与传统的基于几何约束的方法进行了比较，验证了改进方法精度的可靠性；形变实验则验证了改进方法在碰撞物体发生形变的情况下依然有效。根据前期实验研究[25]，系统所涉及的双目立体定位的视觉测量方法精度误差在0.2 mm以内，因此，两组实验都在一套由机械臂和红外双目相机组成的手眼系统中完成，并将视觉定位的结果作为金标准。

实验系统包括：六自由度机械臂1台(UR5，Universal Robots有限公司，丹麦)；红外立体相机1套(北极星系统，Northern Digital 有限公司，加拿大)；六自由度力/力矩传感器(M3813C，日出有限公司，中国)；带有标记点的三维打印的树脂立方体模型1个。在力觉定位实验前，首先通过手—眼标定、传感器和工具标定以及工件(立方体)标定完成机械臂、立体相机、力传感器、末端工具、立方体模型的坐标系的统一，建立系统坐标系，然后通过立体相机和其配套的视觉探针定位立方体上的随机标记点在系统坐标系下的坐标，如图6所示。

4.1 随机点实验

随机点实验的步骤如下：

步骤1将六维力/力矩传感器作为腕力传感器安装在机械臂末端关节上，然后在工具端安装一个探针作为末端工具.

步骤2在立方体模型上随机选取10个标记点作为测试点。

步骤3如图7所示，在视觉引导下使机械臂末端探针抵达测试点，采集碰撞过程中力传感器的数据。

步骤4分别采用传统的基于几何约束的方法和新方法计算力觉感知定位结果。设视觉定位结果为P(x,y,z)，则传统方法检测结果为P′(x′,y′,z′)，改进方法检测结果为P″(x″,y″,z″)。Δ′和Δ″分别为传统方法和改进方法与视觉检测结果相比的误差。图8给出了10个测试点的实验结果。

步骤5从立方体模型3个不同方向的面上各选取2个测试点，然后用改进的方法针对这6个测试点进行10次重复定位实验，用以验证改进方法的收敛性和鲁棒性，实验结果如图9所示。

对比实验结果表明，改进方法的精度和收敛性均优于基于几何约束的方法。重复实验结果的统计数据表明，改进方法的精度于机械臂的位姿无关，且在3个坐标轴上的误差分布没有明显差异。

4.2 形变实验

由于改进的方法不用依赖碰撞物体的表面信息，即使碰撞面发生形变也不会影响检测结果。为了验证改进算法在形变环境下的有效性，本文设计了一组形变实验，具体步骤如下：

步骤1与随机点实验相似，将力传感器和探针安装于机械臂末端。

步骤2在立方体模型上选取10个测试点，运行机械臂，使探针到达测试点，继续施力直至探针发生一定程度的形变，如图10所示。

步骤3收集发生形变碰撞过程中的力/力矩传感器数据，并用改进的方法计算碰撞位置。

步骤4在每个测试点上各重复试验10次，试验结果如图11所示。

5 结束语

正如人类同时具备视觉、力觉、听觉等感知能力一样，力觉感知也是机器人与外界环境交互所必不可少的功能。而基于力觉的碰撞位置感知，是力觉感知系统的重要组成部分。针对现有的基于腕力传感器的触点位置检测方法必须依赖碰撞物体几何信息的不足，本文系统建立了力学数据自约束模型，摆脱了对几何信息的依赖，并基于该模型建立了改进的碰撞检测位置检测方法，提出了一种基于最小误差的搜索策略。实验表明，改进方法的检测精度优于基于几何约束的方法，且精度不受碰撞力大小、机械臂位姿以及碰撞物体的形变程度等因素的影响，具有更好的鲁棒性，能够应用于形变环境。本文所提方法为机械臂作业过程中的单触点位置检测提供了完整的解决方案，未来将进一步研究多点接触时的位置检测问题。