采用数据辅助的大规模MIMO信道半盲迭代估计*

何文旭，张 静，马惠艳

(上海师范大学 信息与机电工程学院，上海 200234)

0 引 言

第五代(5G)移动通信使用大规模多输入多输出(Multiple-Input Multiple-Output,MIMO)技术极大地提升了系统的频谱效率、能量效率和可靠性，已成为5G的关键技术之一[1]。为充分获得大规模MIMO的空间复用和空间分集增益并达到功率效率和频谱效率的极限，需要在有限的导频开销和功率控制条件下获取移动信道衰落参数。

由于大规模MIMO信道矩阵的维度高，与低维MIMO相比获得准确的信道状态信息(Channel State Information，CSI)要困难且复杂许多[2]。信道矩阵的维度很高会导致使用最小二乘估计和最小均方误差估计等优化估计时的逆矩阵求解、奇异值分解、自相关和互相关矩阵的获取和计算困难而难以直接估计；精确的信道估计所需的导频数目在上行链路中与参与空间分集的用户数成正比，在下行链路中与基站端的发射天线的个数成正比，会产生巨大的导频开销而严重降低业务传输速率。为减小在最优估计中由求逆运算带来的计算复杂性，采用迭代方式逐步逼近的期望最大化(Expectation Maximization，EM)算法可得到极大似然(Maximum likelihood，ML)估计的近似值[3]，采用条件期望最大化算法可弱化初值选取对信道估计的影响[4]。

在对信道估计的各类方法[5-17]中，当信道参数非稀疏时，完全基于导频的估计方法所需导频数多，不依赖于导频仅利用信道参数高阶统计量的全盲估计方法计算复杂度高。半盲估计方法折中处理导频数和计算复杂度，通常仅利用少量导频来得到初值，再结合未知数据符号的一阶和二阶统计特性来提高估计精度。本文在对大规模MIMO信道衰落参数获取时，提出了在EM算法框架下采用数据辅助的两种半盲估计算法，考虑了时分双工(Time Division Duplex，TDD)大规模MIMO上行链路，利用EM算法框架来设计半盲的信道估计算法。为避免算法陷入局部最优，通过少量导频序列获取信道衰落参数的初值，同时为降低计算复杂度再根据不同簇内用户的大尺度衰落系数分配噪声，并结合数据符号的后验信息进行完整数据的似然估计。

1 多用户大规模MIMO系接收端模型

考虑一个TDD单小区多用户大规模MIMO传输系统的上行链路。设基站端配备有M根天线，K个配备有单天线的用户随机分布在该小区内，并设M≫K。系统模型如图1所示。

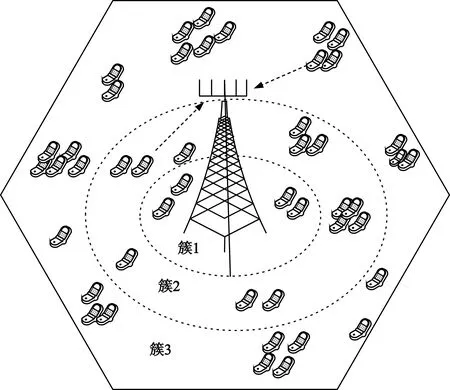
图1 系统模型图

(1)

假定信道为准静态信道，基站端在第n个时刻接收到的信号为

Y(n)=Gx(n)+w(n),n=1,2,…,N。

(2)

(3)

2 基于迭代算法的半盲信道估计

基于导频序列的信道估计方法由于其较低的计算复杂度得到了广泛的应用，但导致了较低的频谱效率和导频污染等问题，因此本文利用少量正交导频序列结合数据符号的统计特性估计大规模MIMO系统的信道衰落参数，但不考虑发送数据符号的解码问题。

2.1 用户发送信号设计

用于信道估计的信号设计如图2所示。K个随机分布在该小区的单天线用户均发送长度为N的信号向量，其中前面长度为Np的信号为正交导频，后面长度为Nd的信号为未知数据符号。

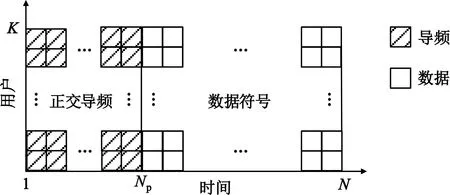
图2 信道估计的信号设计

根据式(2)，并由图2可知基站第m根接收天线接收到的信号向量为

(4)

2.2 获取迭代算法初值

EM算法通过不断迭代逼近ML估计，其初值的选取影响着算法的整个迭代过程，若初值选取不当会影响算法的全局收敛性。根据ML估计算法在接收端利用少量正交导频估计出信道衰落矩阵初值为

(5)

式中：Yp为基站端接收到的导频信号矩阵，Xp为用户发送的导频信号向量。

采用正交导频序列可使式(5)中(XpHXp)-1的值为常数，避免了矩阵求逆。为了得到更加精确的信道估计值，再利用未知数据符号的统计信息，并结合EM算法进行多次迭代估计，直到算法收敛。具体估计过程如图3所示。

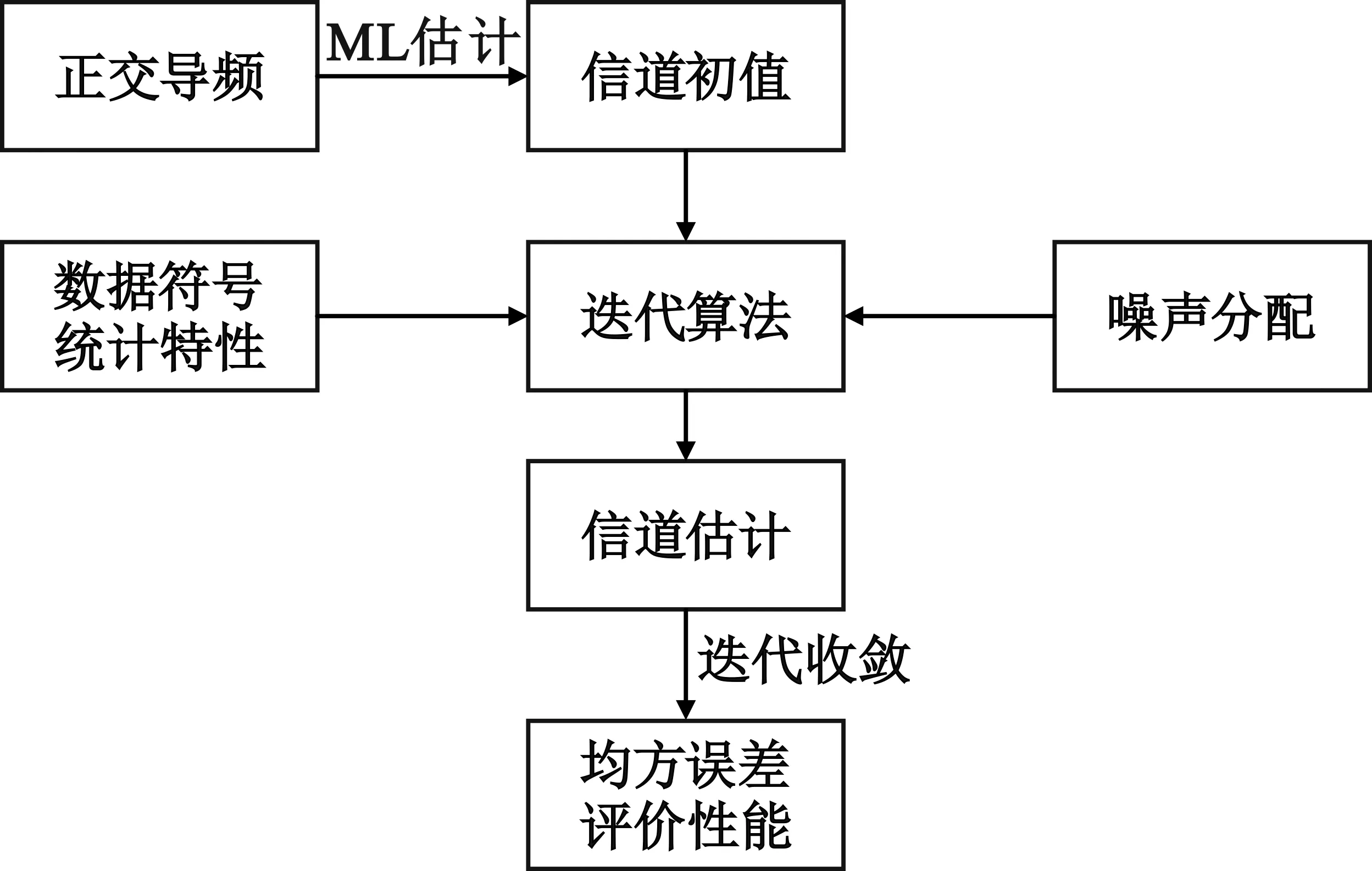
图3 大规模MIMO信道衰落参数的估计过程

2.3 改进的两种EM迭代算法

2.3.1 基于ML估计的EM改进算法(算法1)

为了进一步提高信道估计值的精确性，当基站无法获得准确的发送信号但已知发送信号的一阶和两阶统计特性时，可采用数据辅助的基于EM迭代算法的半盲信道估计。在EM算法中，由于用户发送的数据x隐藏在观测数据Y中，Y是不完整的数据，而(Y,x)是完整的数据。当利用不完整的数据无法估计信道时，需要将不完整数据的似然函数转化成完整数据的似然函数[4]。

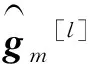
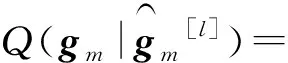
(6)

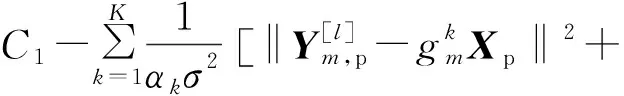
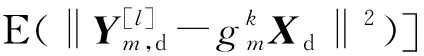
(7)

式中：C1为常数，Ym,p为第l次迭代时基站第m根天线的导频接收信号，Ym,d为第l次迭代时基站第m根天线的数据接收信号。

本文提出一种根据接收噪声分配方式改进的迭代估计算法，它根据用户与基站间信道的大尺度衰落系数把用户分簇。由于大尺度衰落主要与基站和用户的距离有关，因此把用户按照与基站的距离分簇。分簇模型可参照图1，利用不同簇内用户信道的大尺度衰落系数按比例地分配接收噪声。对式(7)中的αk取值为

(8)

经过如式(8)的噪声分配后，使得式(7)的似然函数与用户数无关。由于在不同簇内用户信道的大尺度衰落有所不同，根据大尺度衰落系数按比例分配噪声后，基站端接收的来自不同用户的信号便有所不同。

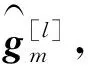
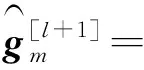
(9)

由式(9)可知，为得到第l+1次迭代的信道衰落的估计值需要计算未知数据符号Xd的期望值。假定未知数据符号Xd满足高斯正态分布Xd～CN(0,1)。将基站第m根接收天线上的信号解耦到k个发送天线上，可知用户在时刻n发送的数据Xd的后验统计量如式(10)和式(11)所示：

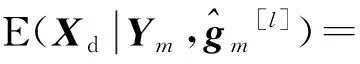
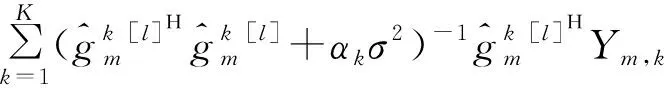
(10)

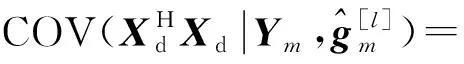
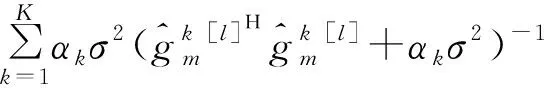
(11)

结合式(10)、式(11)和式(9)可得出基站第m根接收天线第l+1次迭代的信道向量估计值为

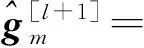
(Xp+u[l])H。

(12)

式中：u表示Nd个时刻发送的数据符号向量均值，Σ表示Nd个时刻发送的数据符号向量方差。

2.3.2 基于牛顿迭代法的EM改进算法(算法2)

由式(12)所获得的迭代估计算法已将高维的参数估计问题转化为较低维的参数估计问题，但在最大化步骤中包括了矩阵求逆的迭代计算，复杂度较高。为了避免矩阵求逆导致的高复杂度问题，利用2.3.1节中所提出的接收噪声按用户大尺度衰落系数分配的方式，推导出较低复杂度且无矩阵求逆的迭代估计算法。

(13)

考虑基站第m根接收天线数据信号的完全数据空间和不完全数据空间的关系为

(14)

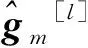
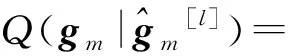
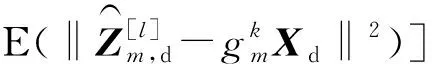
(15)

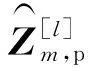
采用算法1中提出的按照大尺度衰落系数分配噪声的方法对αk进行取值，完全数据空间可表示为

(16)

(17)

3 仿真与结果分析

3.1 仿真参数

设一个单小区具有一个中心激励的基站和16个随机分布的单天线用户，每个用户发送长度为256的数据符号，其中正交导频序列的长度为32。距离中心基站小于10 m的用户分为簇1，大于10 m且小于50 m的用户分为簇2，其余用户分为簇3。

对于簇3内的用户，其与基站间的大尺度衰落模型采用Cost-231路径衰落模型：

L(dB)=46.3+33.9lgf-13.82lghB-

(1.1lgf-0.7)hu-(1.5lgf-0.8)。

(18)

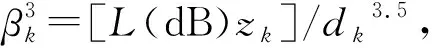
假定无线信道的快衰落部分为瑞利衰落信道，小尺度衰落系数通过一组满足高斯分布的随机数产生。正交导频选自哈达玛矩阵。设每个用户连续发送32个导频符号后发送数据，先估计出128×16个信道衰落的初始值，然后用算法1和算法2得出在不同信噪比条件下的估计MSE。本文定义MSE如式(19)所示，当连续两次迭代的估计值的二范数之差小于10-3时，算法停止迭代。

(19)

3.2 结果分析

将已知完全数据符号时的完美ML估计算法和采用少量导频估计的ML算法分别作为估计性能的上界和下界。图4所示是基站的天线数为128时，提出的两种改进算法的MSE性能随信噪比(Signal-to-Noise，SNR)的变化曲线。从图中可以看出，两种半盲迭代估计算法的性能介于估计上界和估计下界之间，算法2的性能略优于估计上界。

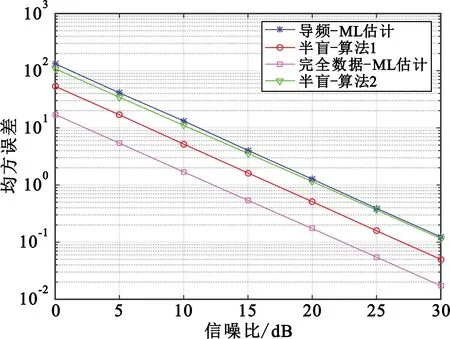
图4 MSE性能随信噪比的变化曲线

图5所示是在信噪比为15 dB和用户数为16时，两种改进算法的MSE与基站天线数量之间的关系。从图中可以看出，基站天线数从102增加到103时，算法1和算法2的MSE均逐渐增大但仍然介于上界和下界之间。

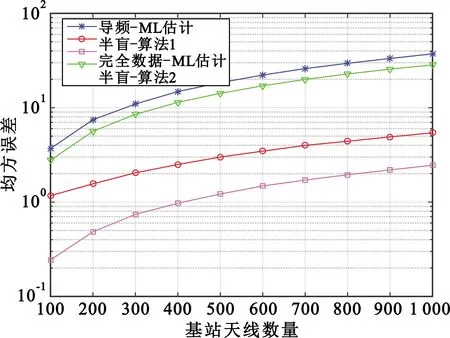
图5 MSE性能随基站天线数量的变化曲线

图6所示为两种不同迭代算法的平均迭代收敛次数与SNR的关系。从图中可以看出，随着SNR的增加，两种改进算法的平均迭代次数均不断减小；改进算法1的平均迭代次数远大于改进算法2，可知算法1的计算复杂度明显高于算法2。

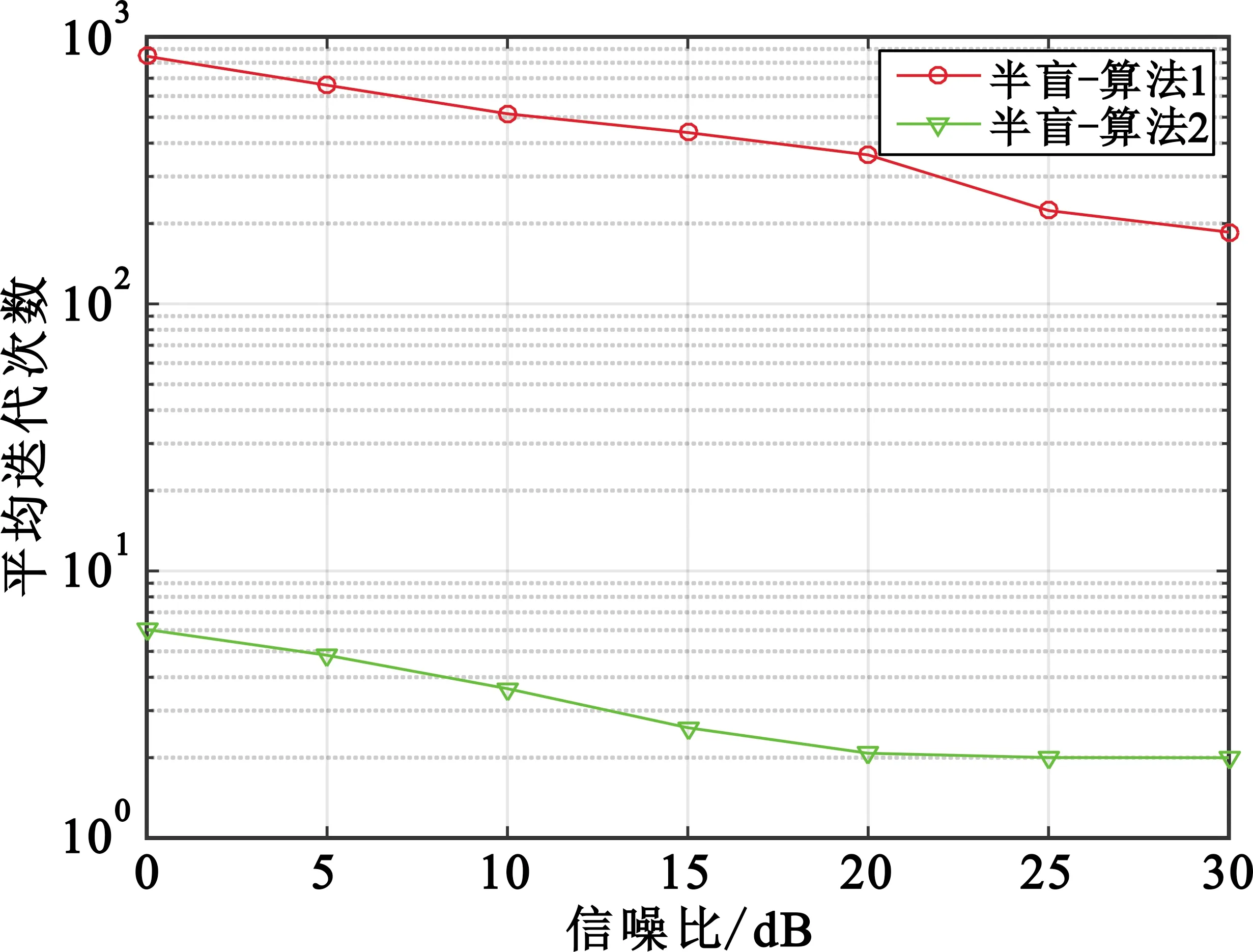
图6 平均迭代次数随信噪比的变化曲线

3.3 计算复杂度分析

本文提出的两种半盲迭代算法在利用正交导频获取初值时的计算复杂度正比于O(MKNp)，在迭代估计阶段的计算复杂度正比于O(MKNd)。在设置迭代终止条件为连续两次迭代的信道估计值的二范数之差小于10-3时，通过仿真SNR与平均迭代次数的关系，可得出半盲估计算法1的收敛速度低于算法2。

4 结 论

本文针对大规模MIMO上行链路传输系统的信道估计问题，提出了两种改进的半盲迭代估计方法。该方法通过用户与基站间信道的大尺度衰落系数把用户分簇，再根据这些系数按比例地分配接收噪声。仿真结果表明，采用该分簇方法的两种迭代算法的性能均优于半盲估计的ML方法。尽管采用了求逆的迭代算法1的性能好于无求逆的算法2，但算法2的计算复杂度远小于算法1，并且随着基站端天线数量的增加，算法2的性能仍然优于仅使用少量导频的ML算法。