LDPC编码MC-LDS系统联合因子图的改进PEG设计*
刘 田,张 毅,余 湋,夏 斌,王 瀚,高 航
(1.中国西南电子技术研究所,成都 610036;2.上海交通大学 电子工程系 上海 200240)
0 引 言
天基物联网利用天基信息传感设备,把世界上地面网络不能连接的物品与国际物联网/专用网络连接起来,实现对物品的智能化识别、定位、跟踪监控和管理,实现物与物、人与物、人与人之间“无处不在,无时不通”的通信。
在天基物联网覆盖的小区远远大于地面小区的前提下,一方面会面临更严峻的时频资源受限,同时接入用户受限的问题格外严重。因此,相较于正交接入方案,非正交多址技术由于可以在相同的资源上接入更多的用户,近年来受到了广泛关注[1-2]。作为基于码域复用的非正交多址接入(Non-orthogonal Multiple Access,NOMA)技术,多载波低密度序列(Multi-carrier Low-density Signature,MC-LDS)技术在解决海量连接的问题方面提供了思路。在MC-LDS系统中,利用发射机处精心设计的低密度序列(Low Density Signature,LDS)矩阵,已编码的比特信息在多个子载波资源上进行扩频[2]。在接收机处,稀疏因子图上的消息传递算法(Message Passing Algorithm,MPA)或置信度传播(Belief Propagation,BP)算法以迭代的方式为MC-LDS 系统实现近乎最佳的多用户检测(Multiuser detection,MUD)[2]。
得益于发送端的资源复用和接收机的非线性检测算法,MC-LDS 系统可实现更高的吞吐量和更多的连接数量。但是,在实际系统中,多用户共用资源引入的多用户干扰是一个严重的问题,对传输可靠性造成了极大的影响。在通信系统中,信道编码作为一种抵抗信道干扰噪声的技术。因此,将MUD 和前向纠错(Forward Error Correction,FEC)码结合起来设计是解决多用户干扰问题的一种可行途径。
低密度奇偶校验码(Low Density Parity Check Codes,LDPC)是一类稀疏的FEC,其性能接近香农容量[3]。LDPC码的解码利用基于稀疏校验矩阵的BP算法来实现,该矩阵可以用一个稀疏因子图等效表示[3]。与传统的串行接收机先进行MUD再进行LDPC译码不同,联合检测译码接收机基于联合稀疏因子图上的MPA[4],该联合稀疏因子图可以将MC-LDS技术的因子图和LDPC码的稀疏因子图结合在一起。联合检测译码接收机在每次迭代中完全交互MC-LDS与LDPC的检测软信息和解码信息,显示出比分别单独译码的方案具有更好的性能。
然而,在目前关于LDPC 码和MC-LDS矩阵构造问题的相关研究中,MC-LDS和LDPC 的构造通常分开进行研究,得到的结果在联合编码调制系统中往往不是最优的[5-7]。在这些方法中,代表因子图中短环长度的围长是特别重要的设计参数,因为当周长较小时,系统的误码性能会变差。但是,MC-LDS 技术与LDPC 码的联合稀疏因子图不仅具有MC-LDS 部分和LDPC 部分的各个环,而且在两个部分之间有交叉的环,这使得较短的环在MC-LDS与LDPC 码的联合稀疏因子图更容易出现。因此,如何在MC-LDS 技术与LDPC码的联合稀疏因子图中找出所有可能的短环情况并优化得到没有较小短环的稀疏因子图的问题也需要解决。
因此,本文基于联合稀疏因子图的度分布,提出了一种改进的渐进边长增长方法来构造特定的联合稀疏因子图。与单独构造MC-LDS或LDPC 的稀疏因子图不同,联合稀疏因子图中有三种不同的节点可以完成软信息的交互,导致在联合稀疏因子图中有三种可能的短环情况。因此,在改进的渐进边长增长方法中,通过联合构造MC-LDS和LDPC 共同组成的联合稀疏因子图,最终获得性能良好的没有短环的联合稀疏因子图。
1 LDPC编码MC-LDS调制系统
1.1 系统模型
如图1所示,考虑一个有K个用户和N个资源的上行多用户通信系统。此时,系统的过载率为β=K/N。假设每个用户都只有一个发射天线,同时接收端也只配置一根接收天线。
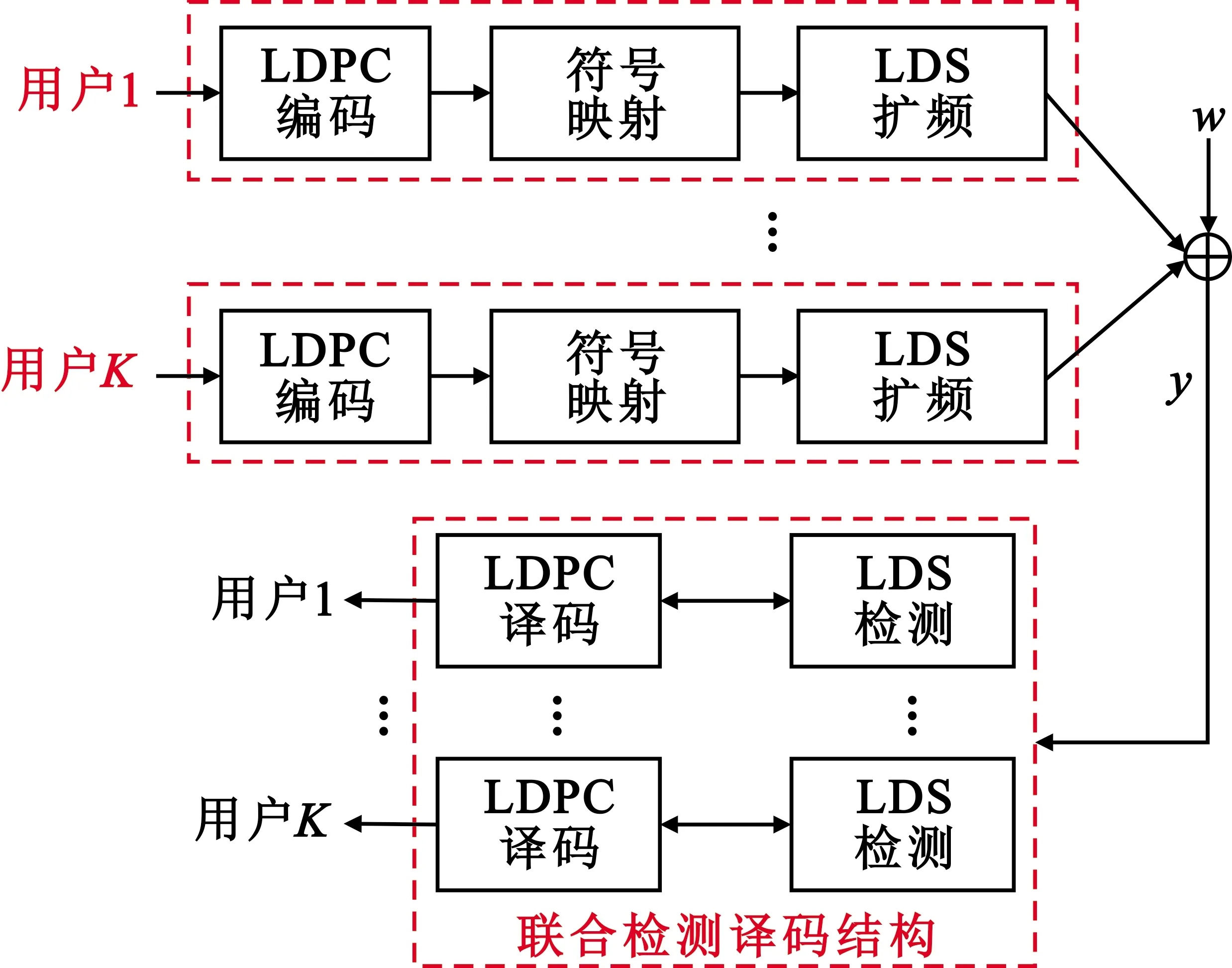
图1 上行LDPC编码MC-LDS调制系统

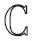
(1)
式中:将rk,n=Aksk,n定义为第k个用户的第m个符号在第n个资源上的扩频增益,同时wm,n~CN(0,N0)表示加性高斯白噪声(Additive White Gaussian Noise,AWGN)。
1.2 联合稀疏因子图表示
基于MPA 方案,MC-LDS的检测和LDPC 的译码可以用如图2所示的联合稀疏因子图表示。
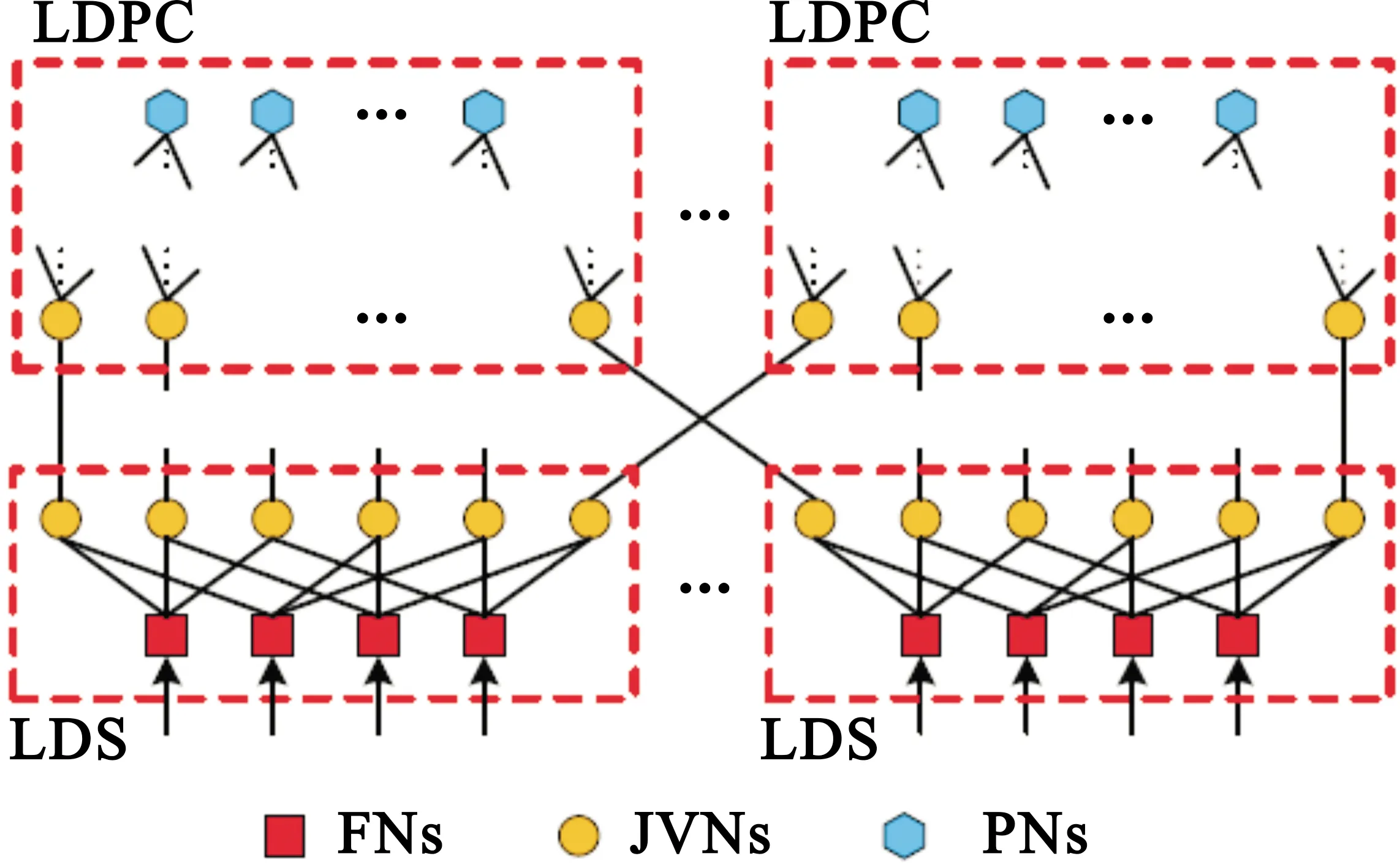
图2 LDPC与MC-LDS的联合稀疏因子图表示
图2中有三种节点,即功能节点(Function Nodes,FNs)、联合变量节点(Joint Variable Nodes,JVNs)与校验节点(Parity-check Nodes,PNs)。其中,JVNs在LDPC码因子图中变量节点对应为每一个比特,而在MC-LDS因子图中变量节点对应为每一个用户。具体地,对于LDS而言,高阶调制后通过低密度扩频序列来映射资源块,低密度扩频序列组成的MC-LDS因子图和LDPC的因子图共同组成联合因子图,因子图中的变量节点就是JVNs。 FNs 和PNs 分别表示MC-LDS矩阵S和LDPC校验矩阵Hk的行,而JVNs 表示这些矩阵的列。这些节点之间的连接关系通过S和Hk中的非零值来确定,而且将S中的非零值用1代替就可以获得MC-LDS矩阵的指示矩阵F,利用指示矩阵可以更加直观表明系统的资源占用情况。图2对应的指示矩阵表示为

(2)
在稀疏因子图中,连接到节点的边数称为节点的度。不规则LDPC 码的度分布由一对生成函数表示[8]:
(3)
式中:λi表示度为i的LDPC 码变量节点连接的边数在LDPC因子图中的总边数中占的比例,dv,LDPC表示LDPC码变量节点的度的最大值,ρi表示度为i的LDPC码校验节点连接的边数在LDPC 码因子图中的总边数之中占的比例,同时dp表示LDPC 码校验节点的度的最大值。
类似地,对于MC-LDS矩阵S,它的度分布的定义可以参考文献[9]中的方法。令γ(x)和ω(x)分别表示MC-LDS矩阵对应的因子图中的功能节点和变量节点的度分布的生成函数,可以表示为
(4)
式中:γi表示度为i的MC-LDS矩阵变量节点连接的边数在MC-LDS的因子图中的总边数中占的比例,df表示MC-LDS矩阵变量节点的度的最大值,ωi表示度为i的MC-LDS矩阵功能节点连接的边数在MC-LDS的因子图中的总边数之中占的比例,同时dv,LDS表示MC-LDS矩阵功能节点的度的最大值。
2 联合稀疏因子图的构造
当给定度分布后,具体的联合稀疏因子图可以利用改进的渐进边增长方法进行构造。原始的渐进边增长方法被用来构造LDPC码的稀疏因子图[6]。此构造方法在变量节点和校验节点之间连续建立起连接,使得每次连接后的图的围长最大。每次边的生成都会通过多次搜索,最终构造的因子图满足围长最大的要求。但是,用这种方法构造的因子图只能保证变量节点的度分布和设定的一致,而校验节点的度分布是随机生成的。为了解决这个问题,在文献[10]的启发下,我们改进了渐进边长增长方法来保证节点(所有的节点)的度分布严格集中在所需值,并使得该方法适合于联合稀疏因子图的构建。具体地,改进的渐进边长增长方法利用节点的自由度而不是节点度来选择用于增加边的节点。该改进的渐进边长增长方法可用于构建MC-LDS矩阵和LDPC 矩阵共同组成的联合稀疏因子图。以构造联合稀疏因子图中的MC-LDS部分为例,图中FNfni的自由度dfree(fni)定义为
dfree(fni)=dmax(fni)-d(fni),i=1,2,…,N。
(5)
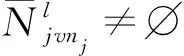
对于具体的联合稀疏因子图,图的围长是另一个非常重要的参数,这在设计实际可用的因子图时需要着重考虑。在我们构造的联合稀疏因子图中,小围长被认为是因子图中girth=4的短环。这些较小的围长降低了节点之间传递的软信息的独立性,并降低了系统的检测译码性能。Gallager[11]的分析表明,在采用基于稀疏因子图的消息传递译码算法时,具有较大围长的LDPC编码系统的性能更加出色。而在LDPC编码的LDS系统中,可以采用基于联合LDPC与LDS因子图的消息传递算法。因此,在联合检测译码结构中,为了获得大围长的联合稀疏因子图,应将设计MC-LDS的矩阵和LDPC 矩阵联合起来构造,使得最终的联合稀疏因子图中没有小围长的短环。对于联合稀疏因子图,如果没有经过仔细构造,小围长在联合稀疏因子图中有三种可能的存在状况,如图3所示。
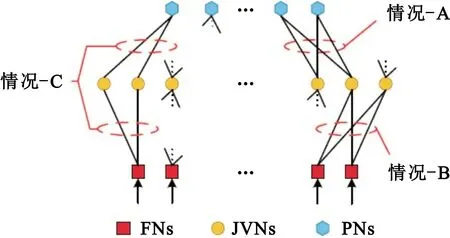
图3 联合稀疏因子图中girth=4的短环
情况A:短环仅出现在LDPC部分中,在LDPC 矩阵的构造中可以避免。
情况B:短环仅出现在MC-LDS部分,在构建MC-LDS矩阵时也可以避免。
情况C:短环包含LDPC部分和MC-LDS部分,需要联合考虑LDPC 矩阵和MC-LDS矩阵的构造才能消除。
对于上述三种情况,在单独考虑LDPC或MC-LDS因子图的构造时,非规则的LDPC码度分布优化会避免情况B短环的出现,MC-LDS的因子图在设计时同样也会考虑避免情况A短环的出现。因此,构建联合稀疏因子图的思路就是在此基础上避免情况C短环的出现。首先利用改进的渐进边长增长方法获得满足最优度分布和围长要求的MC-LDS因子图。在这种构造方法下,联合稀疏因子图中消除了情况B 的小围长的短环。然后,根据图3,利用构造的MC-LDS因子图来创建联合稀疏因子图的MC-LDS部分,而LDPC 部分的构造是基于当前未完成的联合稀疏因子图。MC-LDS部分已经连接好的这些FN 作为特殊PN 参与LDPC 部分的构建,也就是说,它们仅作为中间节点参与JVN 的扩展,从而保证了情况C 的小周长不会出现在联合稀疏因子图中。同样,这里构造LDPC 的方法是修改后的渐进边长增长方法,它避免了联合稀疏因子图中情况B的小围长的出现。在构建了联合稀疏因子图之后,根据指示矩阵F构建MC-LDS矩阵S。
联合稀疏因子图的构造算法的伪代码如下:
1 输入:
J,M,N,K,λ2,…,λdv,LDPC,ρ2,…,ρdp,γ2,…,γdf
/*初始化
2 基于λ2,…,λdv,LDPC和M计算JVNs的度:d(jvn1)≤…≤d(jvnM);
3 基于γ2,…,γdf和N随机生成FNfni的dmax(fni);
4 基于ρ2,…,ρdp和J随机生成PNpni的dmax(pni);
5 设置dfree(fni)=dmax(fni)对于所有的FN;
6 forj=1:Ndo
7 fork=0:d(jvnj)-1 do
8 ifk==0 then
9 在jvnj和fni之间建立边,其中fni是在当前MC-LDS因子图中具有最大自由度的FN;
10dfree(fni)=dfree(fni)-1;
11 else
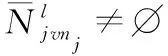
14dfree(fni)=dfree(fni)-1
15 end if
16 end for
17 通过构造的MC-LDS因子图创建联合因子图的MC-LDS部分;
18 基于未完成的联合稀疏因子图和类似的渐进边长增长方法(步骤 6~14)构造剩下的LDPC部分,其中FN替换为PN。
19 输出:F和Hk。
根据上述算法,在已知其度分布的情况下,可构造对应的LDPC校验矩阵与LDS矩阵。具体地,需要先以MC-LDS的功能节点为根,基于改进的PEG算法构造联合稀疏因子图的MC-LDS部分,然后以联合变量节点为根,展开包含MC-LDS功能节点的树,进而构造联合稀疏因子图的LDPC部分。在联合构造过程中涉及两个步骤:第一,以功能节点或联合变量节点展开树;第二,基于树建立新的边。对于所有的用户采用相同的LDPC码。此外,由于在LDS系统中,需要保证每个用户所使用资源的公平性,公式(4)中的ωi对于不同的用户是固定的,因此在构造算法中未将其作为可变的输入参数。
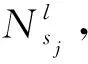
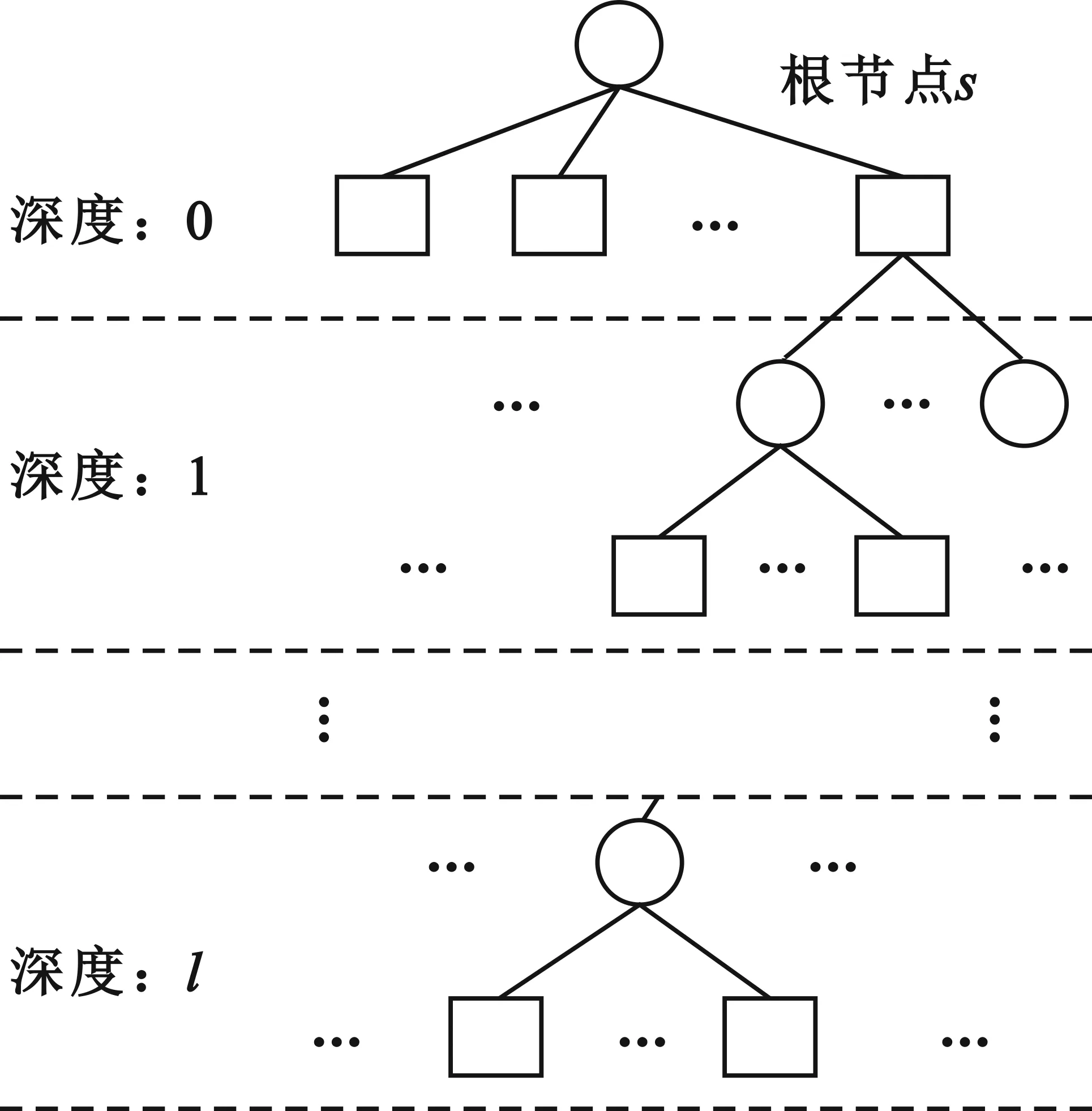
图4 基于因子图的树的展开示意图
根据以上算法,得到的联合稀疏因子图中可以避免图3中第三种短环的出现,进而提升系统性能。
3 性能仿真分析
3.1 仿真条件
在蒙特卡洛仿真中,信道编码采用不规则LDPC码,译码方式采用联合迭代译码。LDPC码长设置为12 096与1 008,码率为1/2。
对于MC-LDS系统,仿真中使用的LDS矩阵的大小设置为8×12。对应的LDS指示矩阵为

(7)
仿真中所使用的LDS矩阵为
(8)
此外,其他的仿真参数如表1所示。

表1 仿真参数
3.2 仿真结果与分析
当构建一个具体的联合稀疏因子图时,短环对BER性能的影响如图5所示。其中,因子独立优化时,LDS与LDPC各自的girth均大于4,而联合LDS-LDPC则存在girth为4的情况(见图3);而在因子图联合优化时,每个部分的girth均大于4,消除了如图3中所示的girth为4的短环。此外,所有用户采用相同的LDPC码校验矩阵。从图5中可以看出,没有图3中girth=4的短环时,对于LDPC码长为12 096与1 008时,系统在BER为10-5时能分别带来大约0.5 dB与0.6 dB的性能增益,表明消除联合稀疏因子图中的短环可以进一步提高性能。因此,很有必要利用算法所描述的联合渐进边长增长的方法来构造联合稀疏因子图。
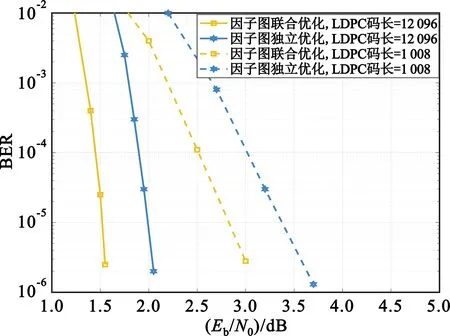
图5 联合稀疏因子图构造算法BER性能仿真
4 结束语
本文针对联合稀疏因子图中信息的充分耦合特性,提出了一种将LDPC码与MC-LDS进行联合分析设计的方法,通过利用改进的渐进边增长方法构建性能良好的联合稀疏因子图,优化设计了联合稀疏因子图的连接结构。所提方案在BER为10-5时具有0.5~0.6 dB的性能提升。本文基于传统的MPA联合迭代算法研究了联合稀疏因子图的构造,而在未来的工作中,将接收端的联合译码算法设计和联合稀疏因子图的构造结合起来,也可以用来减小编译码复杂度与提升性能。因此,联合接收机算法与稀疏因子图设计是后续考虑的一个研究方向。

