基于深度学习的毫米波系统波束成形*
龙 恳,王亚领,陈 兴,王 奕,谭路垚
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引 言
目前,毫米波大规模多输入多输出(Multiple-Input Multiple-Output,MIMO)的瓶颈问题是如何快速准确地获取上行信道和下行信道的信道状态信息。近几年来,深度学习已经成功应用于无线通信系统,例如毫米波信道估计[1]、信道状态信息反馈与信号检测等。对于信道估计,深度学习方法尚未得到全面的研究,尤其是在毫米波大规模MIMO系统中。
传统的信道估计主要分为时域信道估计和频域信道估计。文献[2]研究了时分双工(Time Division Duplexing,TDD)模式下毫米波大规模MIMO训练序列设计和信道估计优化算法,在提高估计精度的同时降低训练开销和算法复杂度。如何快速高效地获取下行信道状态信息成为了当前硏究的主要热点。为了解决系统信道估计问题,现有文献多釆用了闭环的信道估计结构[3]或者基于稀疏压缩感知的信道表示方法[4],通过利用信道矩阵的空时相关特性来减小有效信道维数。然而这些方法仍然依赖于高维的信道统计信息,因此训练和反馈开销仍然庞大。文献[5]提出了一种基于波束训练的信道跟踪算法,克服了文献[6]中几何模型对信道跟踪的限制。简而言之,如何根据毫米波大规模MIMO天线的架构特征和特殊的信道特性,设计普适于时分双工/频分双工系统的准确高效的信道估计算法是提升毫米波大规模MIMO系统频谱有效率和能量效率的关键所在[7]。毫米波大规模MIMO系统相比于传统的MIMO系统,在天线架构和信道建模方面有着很大的不同。天线数量的增多使得信道估计、预编码设计、信号检测等方面的计算复杂度都大大增加,系统效率的提升是目前所面临的难题。因此,必须设计低开销、低复杂度的算法来克服毫米波大规模MIMO系统所带来的这些问题。
本文提出一种新颖的集成深度学习协调波束成形(Deep Learning Coordinated Beamforming,DLCBF)解决方案来代替传统方法估计下行信道,通过训练学习上行链路获取下行链路的波束成形向量信息。采用多个基站同时对一个终端考虑非完美信道下(多普勒频移、电磁屏蔽、物体周围路径损耗、终端移动速度等)协调多个基站(Base Station,BS)波束成形,解决BS与移动用户之间频繁切换影响信道速率的问题。应对时变场景,使训练模型具有高鲁棒性,而且本文方案在频段适用方面具有较强的兼容性。仿真结果表明,所提出的DLCBF与传统的毫米波波束成形策略相比有更高的频谱效率(接近上限),并且比现有的传统方案具有更好的性能。
1 系统模型与问题描述
1.1 系统模型
如图1的毫米波通信系统,有N个BS同时服务于同一个终端(Terminal,TE),每个BS都有M个天线,且所有的BS都连接到云服务器端。此处只考虑每个BS只有一个射频(Radio Frequency,RF)链路,并且使用移相器网络应用模拟波束成形。为简单起见,假设用户只有一个天线,但是开发的算法和研究解决方案可以扩展到多天线用户。
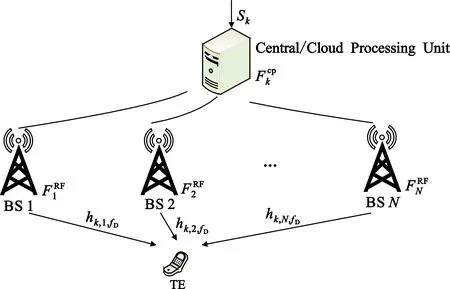
图1 毫米波波束成形系统模型
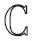
(1)
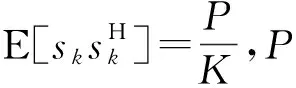
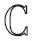
(2)
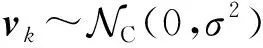
1.2 问题描述
在高速移动(High Speed Mobile,HSM)场景,高速移动的用户会带来不可忽略的多普勒频移,从而导致了额外的载波间干扰。为了简化模型,没有考虑来自其他单元或者其他用户的干扰,主要考虑基站和用户之间的信号转换。信道模型如图2所示。
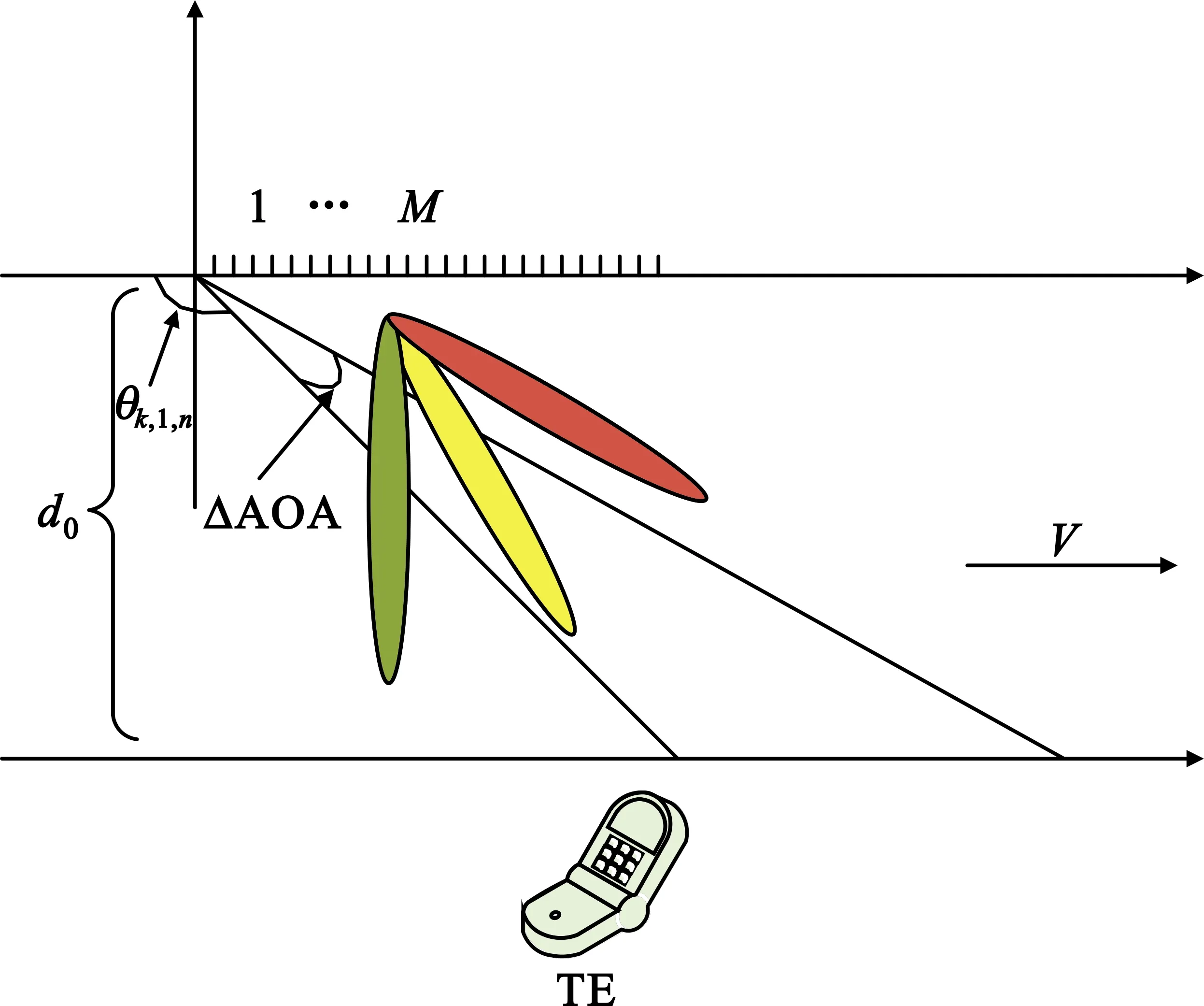
图2 高速移动场景下MIMO信道模型
在HSM中,非视距路径下信号信道增益较视距路径下信号强度弱很多,即信道模型仅考虑视距路径。采用L个簇的几何宽带信道模型[8],每个簇(=1,2,…,L)假设为有一条有时间延迟τ∈和到达角的方位角/仰角的光线。然后,把ρn表示为终端和第n个基站之间的路径损失,p(τ)表示为时间延迟向量。综上所述,用户与第n个基站之间的信道模型可以写为
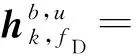
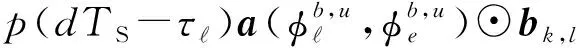
(3)
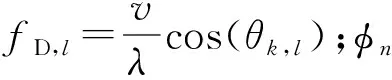
(4)
2 问题求解
文献[11]研究了一种在高速移动情况下的MIMO系统的稀疏信道估计方法,极大地避免了利用时域的稀疏性来估计大量的信道系数。本文主要对移动场景下设计出一种更加有效的波束成形方案降低计算复杂度,提高频谱有效率。
如图3所示,终端先在上行链路发送导频信号,基站处通过全向接收模式和预定义码本通过基站处理后发送到云端,在云处理器端训练出一个合适的协调波束成形模型,然后基站处只通过全向接收模式接收上行导频信号即可以得到合适的下行链路波束向量,使系统有更好的频谱有效率。
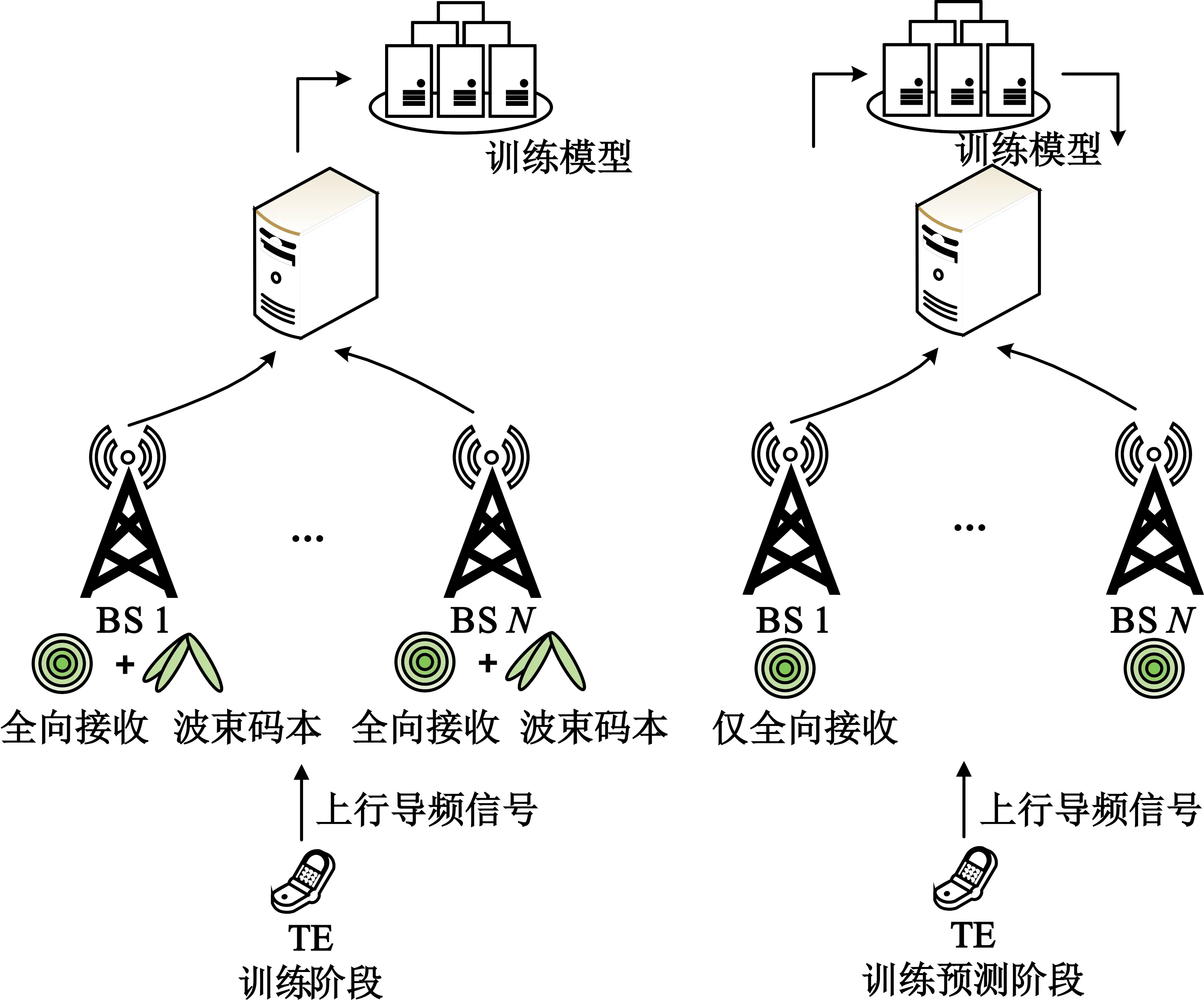
图3 协调波束成形系统模型
根据上述信道模型,用户的频谱有效率可以表示为
(5)
(6)
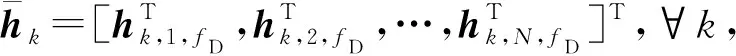
(7)
即产生最佳频谱有效率的波束向量为
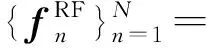
(8)
频谱有效率为

(9)
频谱有效率包含了用户移动性对实际信道数据速率的影响。本文主要目的是研究一种较为有效的信道训练和波束成形的设计策略,以达到补偿信道中多重因素的影响并最大化系统频谱有效率,即最终问题解决方案可以表示为
(10)
2.1 深度学习协调波束成形
针对传统的通信系统,文献[12]提出了一种基线协调波束成形(Baseline Coordinated Beamforming,BLCBF)解决方案。在过去几年里机器学习开始逐渐应用于很多场景下,其优点主要是能够做出成功的预判。本文介绍毫米波系统下协调波束成形中机器学习的一种新颖的应用方案,该方案具有较低的复杂度,能减小训练开销,降低延迟。
2.1.1 训练学习阶段
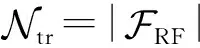
(11)
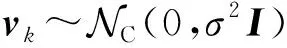
(12)
然后将所有的波束成形码本的组合信号从基站反馈到云服务器端,云服务器端根据每个RF波束成形矢量计算接收功率,并根据计算功率选择BS的下行链路波束成形向量:
(13)
2.1.2 预测阶段
将波束训练导频序列时间表示为Tp,频谱有效率表示为
(14)
系统依赖于训练的深度学习模型和从基站处捕获的全向接收信号来预测RF波束成形向量。简单来说,基站侧使用全向接收每个波束相干时间内用户发送上行导频序列和预处理的码本进行组合,反馈到云处理器;云处理器通过深度学习模型预测最佳的RF波束成形向量,以最大化每个基站中频谱有效率;预测的RF波束成形向量在基站处组合下行导频序列,并估计有效信道。深度学习预测阶段,系统的频谱有效率为
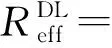
(15)

2.2 深度学习模型
本文所提出的DLCBF依赖于全向接收信号来预测波束成形方向。基于此,将神经网络模型的输入定义为从N个基站收集的正交频分复用全向接收序列,输出为每个RF波束成形向量所预测的速率。本方法采用卷积神经网络(Convolutional Neural Networks,CNN)模型,结构如图4所示。
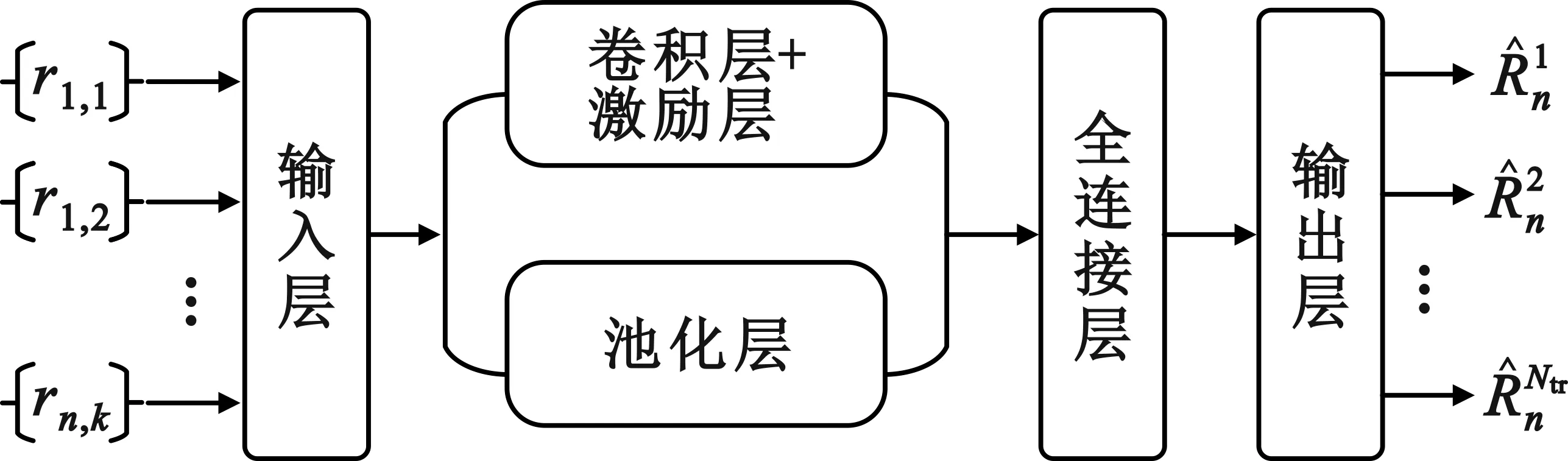
图4 CNN模型结构
卷积层利用卷积核进行局部感知,通过反复多次的滑行卷积操作得到输入层的全部特征。之后连接池化层,在卷积层获得特征之后,直接学习这些特征分析容易出现过拟合的问题,使用池化层进一步调整卷积层的输出。这样能够降低特征冗余度、运算量和网络参数,过拟合问题也会在一定程度上得到改善。然后通过全连接层进行预测每个基站具有最高的速率所对应的最佳波束成形向量,此处采用回归学习模型,神经网络进行训练以最小化损失函数,定义为
(16)
3 仿真与分析
3.1 仿真设置
由于DLCBF依赖于数据收发器的位置、位置几何形状与波束成形之间的相关性,即信道参数生成数据是非常重要的,所以,采用射线追踪模式来仿真该场景,具体参数如表1所示。
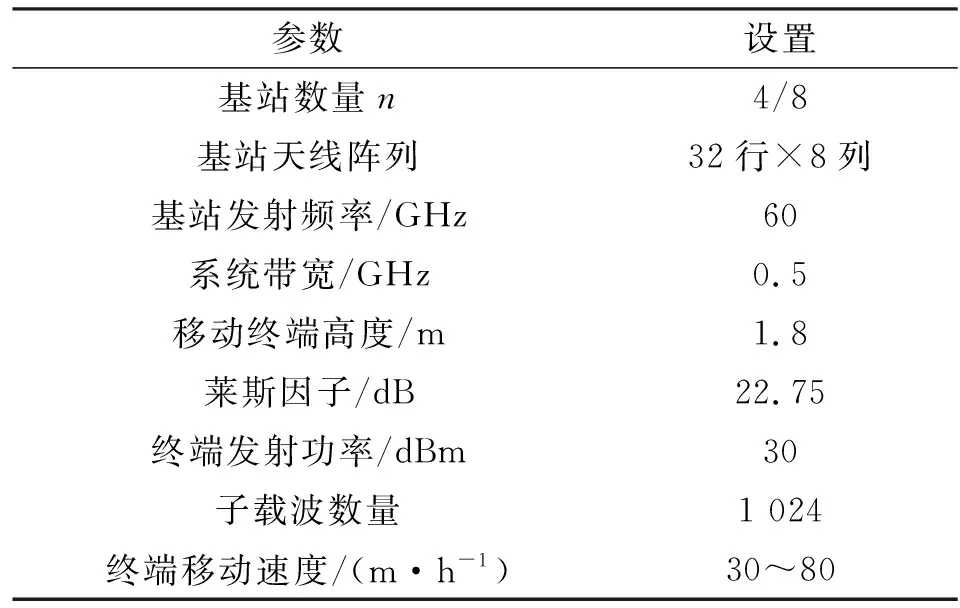
表1 系统仿真参数
深度学习模型采用简单的全连接层模型,每个基站有2N个输入,它是N个基站的全向接收序列的实部和虚部,且有Ntr个输出,模型的输出代表的是频谱有效率的波束成形向量。神经网络模型具有6个全连接层,每层设置512个节点,完全连接层使用ReLU激活单元节点,并且将每层的drop-out设置为0.5%,在实验过程中使用Keras库和TensorFlow。
3.2 仿真分析
本节通过仿真对DLCBF、BLCBF和F-ChanEstNet方案的性能进行评估并与其性能最优上界Genie-Aided进行对比。
图5展示了几种不同方案中系统频谱有效率与数据集大小之间的变化关系,该图考虑了4个基站的视距场景下,服务于一个以50 m/h速度移动的车辆。通过仿真分析可以发现,随着数据集的增多,BLCBF方案中系统频谱有效率缓慢增长,但增长趋势不明显,这是因为此方案需要进行详尽的波束训练,会消耗大量的训练资源并显著降低传输速率。F-ChanEstNet方案中系统的频谱有效率逐步增加,但并没有本文方案的性能提升明显,主要原因是F-ChanEstNet方案适用于速度较大的场景,而本文方案可以适应不同速度对用户信道所带来的影响,增长变化趋势是先快后慢,然后趋于平稳,并接近性能上限。Genie-Aided表示在特定系统中信道模型的任何其他信道训练和波束成形策略的性能上限,接近此界限说明了所提出的解决方案的最优性。
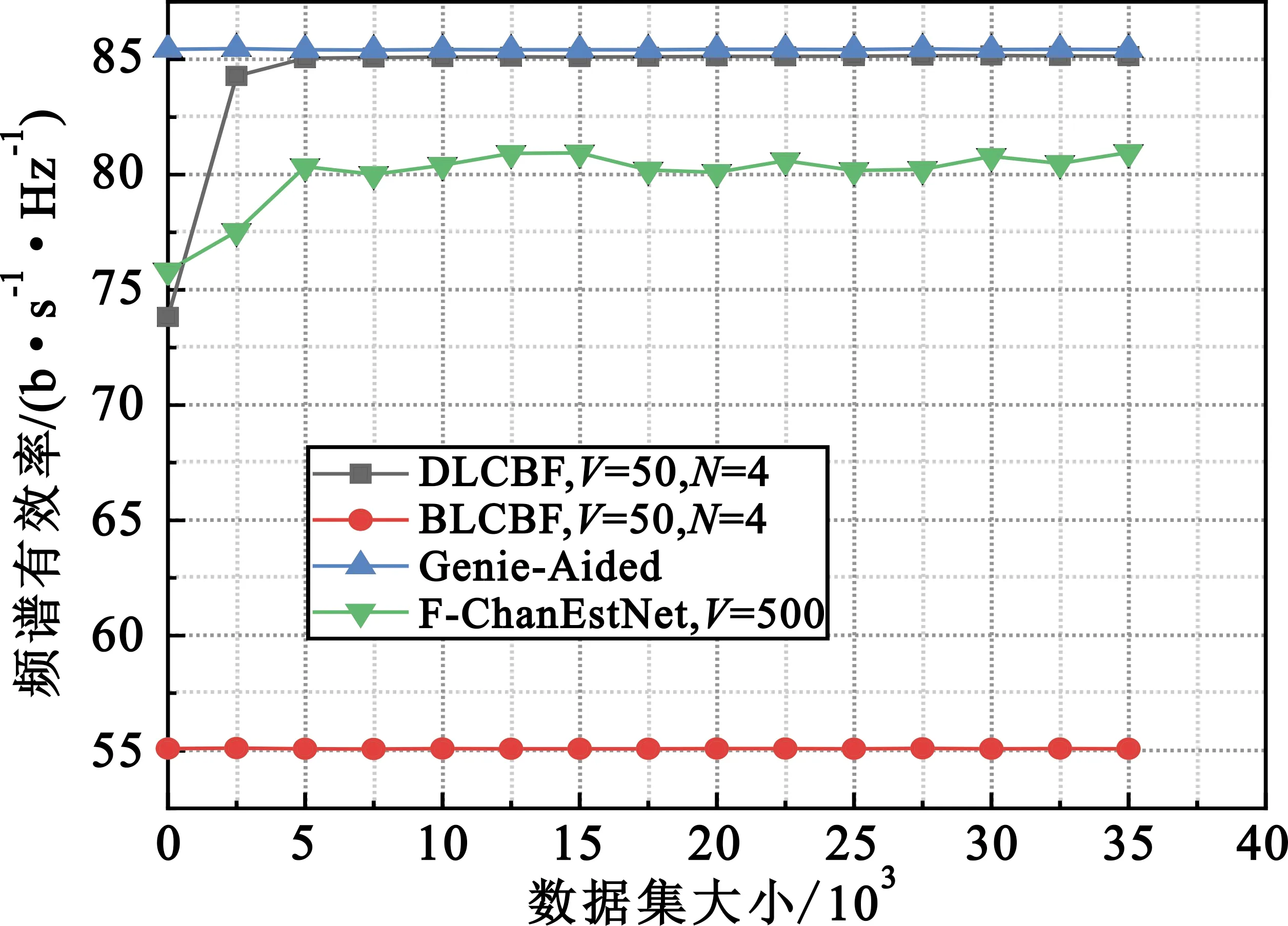
图5 不同方案的比较
图6展示了深度学习模型系统中4个基站为不同速度的终端服务,系统的频谱有效率的变化趋势。从图6可以看出,同一模型下,不同终端速度所带来的信道影响在该模型处理下系统效率差别很小,系统速率随着数据集增大而增大,变化趋势都是先快后慢,然后趋于平稳,但增幅很小,这也正说明了此模型对终端用户信道中由速度所带来的影响的适用性,同时也可以说明该方案适用于现在的很多高速移动的场景。
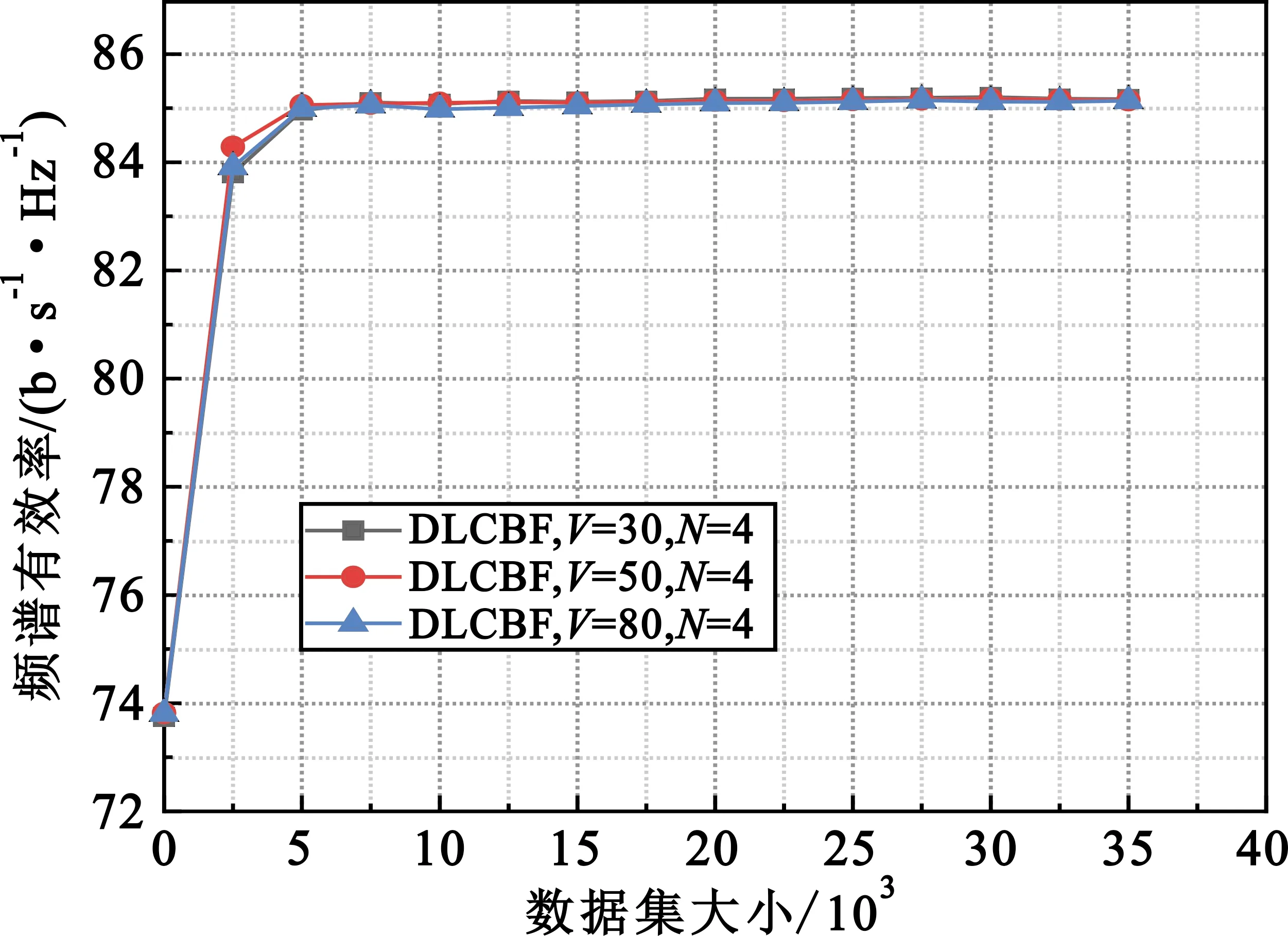
图6 DLCBF系统中终端速度的影响
图7展示了深度学习波束成形方案中不同基站数对同一用户服务。通过仿真分析可以发现,随着基站数量的增多,系统的频谱有效率相应提升。多基站协调波束成形策略可以大大减少终端用户在基站之间频繁切换,相应地系统频谱有效率会提高。但是随着数据集的增大,基站数量的增加并不能使频谱效率显著增加,原因是终端用户与距离过远的基站信号传输衰减比较严重,而且基站数量的增加必定使系统的能耗增加。
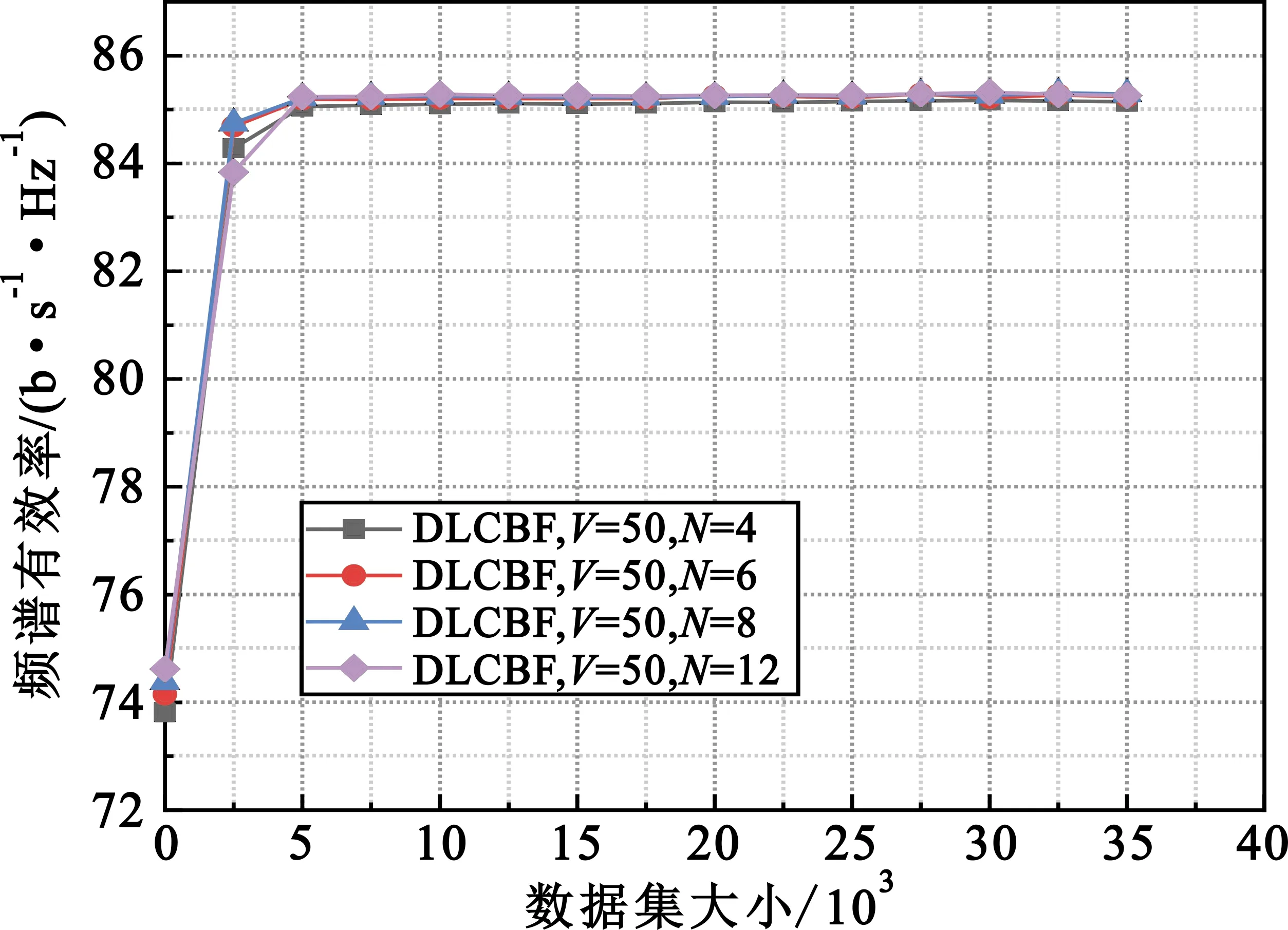
图7 DLCBF系统中基站数量的影响
4 结束语
本文提出了一种集成机器学习和协调波束成形策略的方案,可以实现大阵列天线毫米波系统中的高移动性应用。本文只考虑了单个用户与基站之间的通信,实际场景中会涉及多用户多基站之间的通信,因此本文可以作为后续研究的基础,且本文算法同样适用于多用户多基站系统。下一步的研究可以扩展到多用户系统中,并考虑用户之间的干扰,研究更为复杂的毫米波波束成形机器学习模型,以及不同波束成形方案各个性能的最优解。

