一种超宽带与惯导融合的LSTM室内定位算法*

李鹏杰，李晓青，王瑞雪，邱金娜，刘俊鹏

(1.航天恒星科技有限公司，北京 100095；2.重庆大学 微电子与通信工程学院，重庆 400044)

0 引 言

随着现代社会的生产活动对安全性要求的提高，在水电站等复杂室内环境下，人员定位、物体定位等室内高精度定位需求不断增加。在开放环境中，超宽带(Ultra-wideband,UWB) 定位技术的定位精度可达厘米级[1]。但是，在复杂非视距(Non-Line-of-Sight,NLOS) 室内环境中，障碍物的遮挡会导致较大的UWB测距误差[2]，甚至造成信号传输中断从而导致定位失败。惯性导航技术[3]作为自主导航技术，不受周围环境影响，但随着系统运行时间的增加，会出现误差累积的情况。为了解决单一室内定位技术在复杂非视距环境下遇到的技术瓶颈，联合定位技术应运而生。联合定位技术将单一的定位技术组合起来，辅以数据融合算法进行信息融合，用以满足室内定位系统在高精度、实时性、低功耗、低成本等方面的需求。高精度室内联合定位技术的实现，对在工厂、水电站等复杂非视距环境下人员定位、室内机器人定位等高精度室内定位需求的实现有着重要的意义。

对于机器学习算法在室内定位中的研究，国内外都做了大量工作。目前，被引入到室内定位技术中的机器学习方法包括贝叶斯分类算法[4-5]、支持向量机[6-7]、决策树[8-9]、人工神经网络算法等[10]。朴素贝叶斯分类简单易实现，但其计算量较大，且有强独立性要求。支持向量机分类回归能力突出，但其核函数敏感，仅在二分类问题效果显著。决策树算法计算成本低，但其建树层级过深时易存在过拟合缺陷。人工神经网络可通过模型训练过程自动提取系统特征[11]，省却了非线性映射和系统模型构建的步骤，尤其是在噪声复杂度较高的情况下表现优异，适用于数据量较大、模型构建复杂的定位系统。使用传感器时序数据对定位点位置进行估计可被视为一种时间序列预测问题[12]。而在人工神经网络算法中，循环神经网络算法在序列数据处理上表现优秀，适用于基于无线通信的室内定位系统。

1 联合定位算法结构

1.1 总体架构设计

图1展示了本文提出的基于长短时记忆(Long Short Term Memory,LSTM) 神经网络的联合定位算法的总体架构。由于采集到的UWB测距信息与惯性测量单元(Inertial Measurement Unit,IMU)传感器信息都具有时域连续性，而LSTM在时间序列数据预测上有充分的理论优势，因此本文选取LSTM作为联合定位算法中的核心算法。

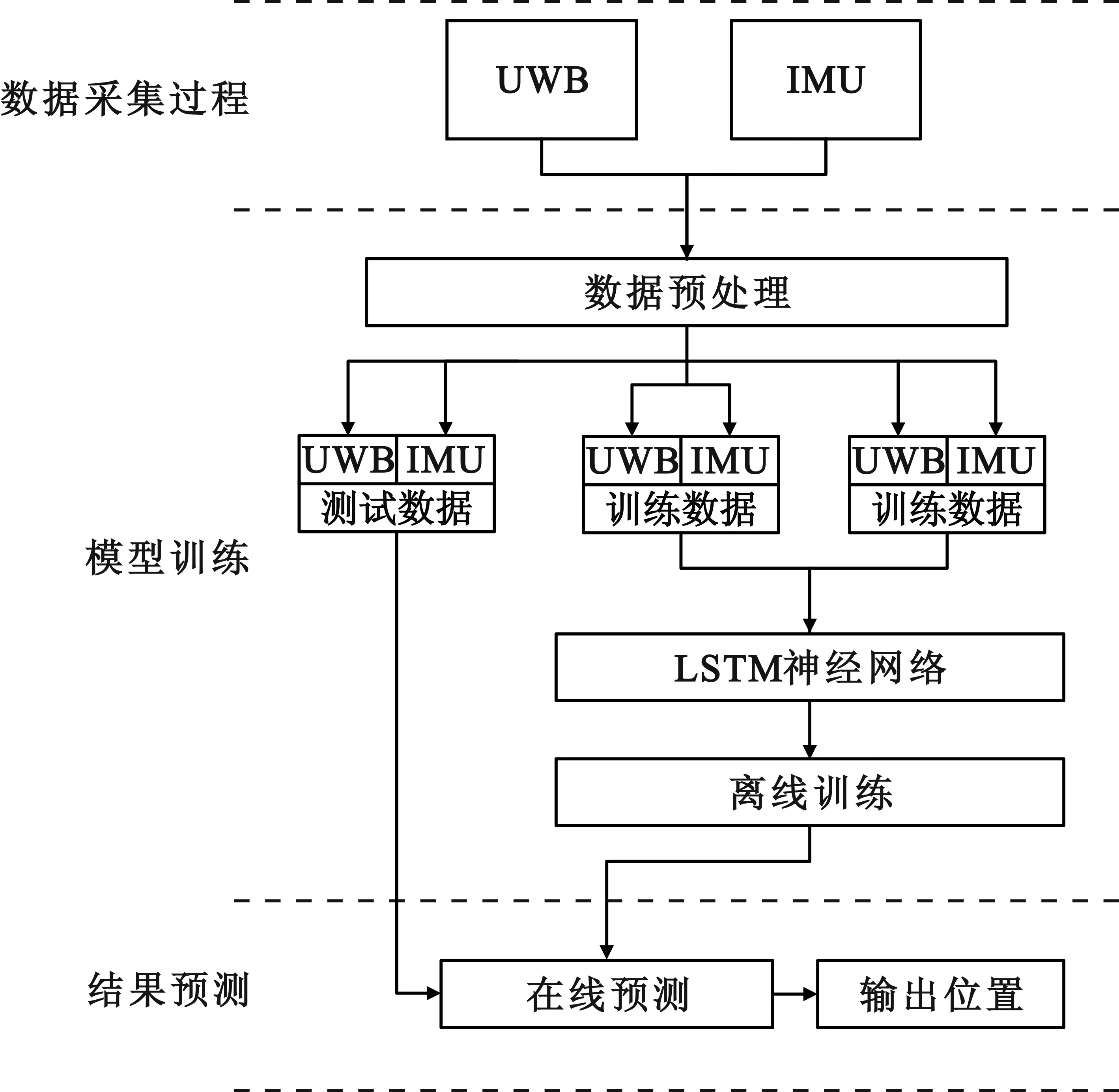
图1 LSTM定位算法架构图

整个联合定位的算法过程可以作如下描述：首先使用室内联合定位系统对超宽带测距信息与惯性测量单元的测量信息进行采集，接下来对采集到的信息进行批处理和归一化，而后作训练集和测试集的划分，对于训练集的数据使用LSTM深度神经网络进行离线训练，得到训练出来的模型。得到训练模型后，以此模型结合测试集进行在线预测，得到估计的位置结果。

1.2 数据预处理

数据预处理过程的合理性直接影响着整个神经网络算法最后的估计结果精度。在本文中数据预处理过程包含数据粗滤波、数据规整、归一化等过程。具体的数据预处理过程为：在采集到原始的UWB测距数据和IMU测量数据后，通过数据粗滤波去除掉其中错误的数据(如测距信息为负值的数据)，再将UWB测距数据和IMU测量数据进行数据规整得到同一维度的数据矩阵，最后通过数据归一化处理得到最终数据。

本文在对UWB测距数据和IMU测量数据进行处理的时候都选用同一种数据归一化方法，即最大最小值归一化法。由于在标签运动过程中位置信息和IMU测量信息的变化幅度都不确定，但是都维持在一个相对低速的状态，同时也为了后续训练时处理方便，需要归一化处理数据。以UWB测距信息为例，最大最小值归一化法的公式表示如下：

(1)

式中：Enorm为UWB测距值归一化后的值，Esig是UWB测距原始数据矩阵中的值，Vmin为UWB测距数据矩阵中的最小值，Vmax是数据矩阵中的最大值，Vmax-Vmin为UWB测量数据极值。IMU测量数据在本文也通过同样的方式进行数据归一化映射。

1.3 网络架构设计

本文中的LSTM网络结构在设计时采用Bi-LSTM(Bidirectional LSTM)层来替代基本LSTM层，并且在网络结构中引入注意力(Attention) 机制。相比于基本LSTM结构，Bi-LSTM具有时序数据利用率高的特点[14]。Bi-LSTM结构由两个方向相反的基本LSTM构成，可以利用超宽带和惯导数据的前后信息来对当前数据进行判定。Attention机制最初被用于自然语言处理领域，通常被用于Bi-LSTM层后面。本文中使用Attention层区分输入的传感器信息的重要程度。图2为本文设计的LSTM联合定位算法的网络结构。

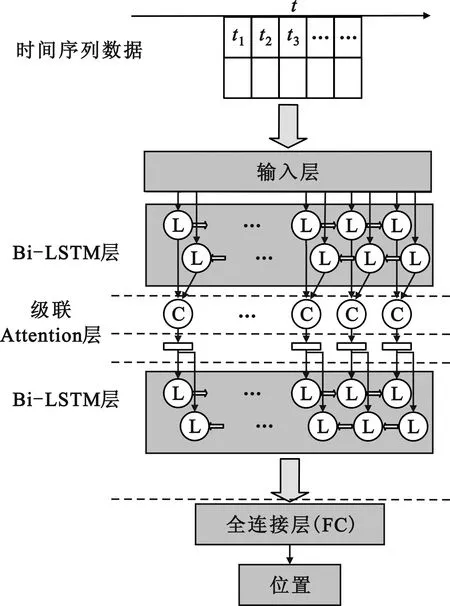
图2 LSTM定位算法网络结构图

由图2可知，本文提出的LSTM网络结构分为输入层、隐藏层和输出层三个部分。UWB测距和IMU测量时间序列数据依次通过输入层、隐藏层和输出层处理，最后得到一个位置信息的估计值。

输入层是LSTM网络结构中用于接收及预处理传感器序列数据的部分。隐藏层是LSTM网络结构中除输入层和输出层之外的部分，由两个Bi-LSTM层和它们之间的级联模块以及Attention模块组成。第一个Bi-LSTM层用于处理输入层的输出数据，该层由若干对LSTM单元构成，单元数量与输入层的输入窗口大小一致。接下来经过一个级联模块以及Attention模块，而后传递给第二个Bi-LSTM层。级联模块用于连接两个Bi-LSTM层。Attention模块赋予不同传感器数据以不同的权重，用于区分不同传感器数据之间的重要程度差别。第二个Bi-LSTM层由100对LSTM单元构成。

输出层则是由一个全连接层构成，通过对单元进行全连接处理，降低数据维度，输出LSTM网络估计得到的最终结果，也就是位置估计值。全连接层的激活函数选用ReLU(Rectified Linear Units) 函数。ReLU函数可解决激活函数带来的梯度消失问题[15]，相较于sigmoid激活函数，ReLU可以将取值映射到所有正数域。

1.4 模型训练方法

本文中LSTM神经网络算法最终的目的是为了更加准确地估计出定位点的位置。基于此，本文提出的损失函数如下所示：

(2)

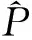
为了得到模型的最优解，本文使用Adam优化器[16]来对模型进行优化处理。

2 联合定位仿真实验

为了说明基于LSTM神经网络的联合定位算法的准确性，本节将通过相应的仿真实验，对标签在菱形和圆形运动轨迹下使用两种联合定位算法的定位准确度进行对比分析。下列仿真实验均在配备六核Intel i7-8700k CPU、英伟达1080Ti GPU的电脑上完成，仿真编程语言选用Python，深度学习框架为TensorFlow 1.12.0。

在前文所述的仿真环境中，让标签沿着菱形运动轨迹运动，与此同时，采集到标签的UWB测距信息以及惯导传感器数据，并分别以TOA定位算法、UKF联合定位算法、LSTM神经网络联合定位算法对位置进行估计。图3为三种定位算法的定位点估计结果与真实点的对比分析图。由图3可知，在三种定位算法的对比中，在准确度上LSTM神经网络联合定位算法明显高于UKF联合定位算法以及TOA定位算法。

图3 定位估计点轨迹

图4为三种定位算法的估计轨迹与真实轨迹的距离误差的累积概率分布函数(Cumulative Distribution Function,CDF)对比图。由图4可知，距离误差30 cm以内，LSTM神经网络联合定位方法的估计点的累积概率为97.35%，UKF联合定位方法的估计点的累积概率为86.93%,TOA定位方法的估计点的累积概率为49.3%。

图4 距离误差CDF

由三种算法的CDF对比图可知,LSTM神经网络联合定位算法的定位精度优于UKF联合定位算法。在直观地对于三种定位算法的定位结果进行对比后，下面对三种定位算法的估计轨迹与真实轨迹之间的误差进行定量分析。表1给出了在菱形运动轨迹仿真实验中，三种定位算法的均方根误差(Root Mean Square Error,RMSE) 对比。

由表1可知，LSTM神经网络联合定位算法相比UKF联合定位算法，真实点与估计点之间的距离RMSE从24.18 cm下降到15.83 cm，相比而言，定位误差下降了34.53%。由此可得，在菱形轨迹仿真实验中，LSTM神经网络联合定位算法表现优于UKF联合定位算法。

表1 定位算法RMSE对比表

3 联合定位实验测试

在理解了UWB和惯导室内联合定位系统的工作原理以后，为了验证UWB和惯导联合定位算法在实际环境中对于UWB定位系统的精度提高作用，我们专门设计实现了一套室内联合定位系统。本节将在此联合定位系统上进行功能测试实验以及动态联合定位实验，验证联合定位系统的功能以及前文提出的联合定位算法在实际环境中的性能。

3.1 实验环境与硬件平台

本次实验选择的环境为实验楼的某一房间，房间总长为8.34 m，宽度为5.76 m，高度为2.62 m。房间内部被清理出一片空旷区域，以便后文构建视距和非视距实验环境。

在此次实验中，共使用4个定位基站，基站按照矩形的4个顶点的分布形式分布，分别为(4.65,-0.1)m、(4.65,3.1)m、(-0.5,3.1)m、(-0.5,-0.1)m。如图5所示，定位标签被固定在巡线机器人上，标签安装高度为25 cm。图6和图7是联合定位系统的定位基站和定位标签。

图5 巡线机器人

图6 定位基站实物图

图7 定位标签实物图

为验证联合定位算法在不同实验环境中的定位效果，在定位区域中依次添加1号障碍物、2号障碍物、3号障碍物、4号障碍物，并对定位标签在障碍物数量不同的情况下的定位结果进行对比分析。其中，1、2、3号障碍物都为铁制电脑机箱，长为43 cm，宽为18 cm，高为40.5 cm；而4号障碍物为饮水机，长为29 cm，宽为29 cm，高为83 cm。图8展示了4个障碍物的放置位置。

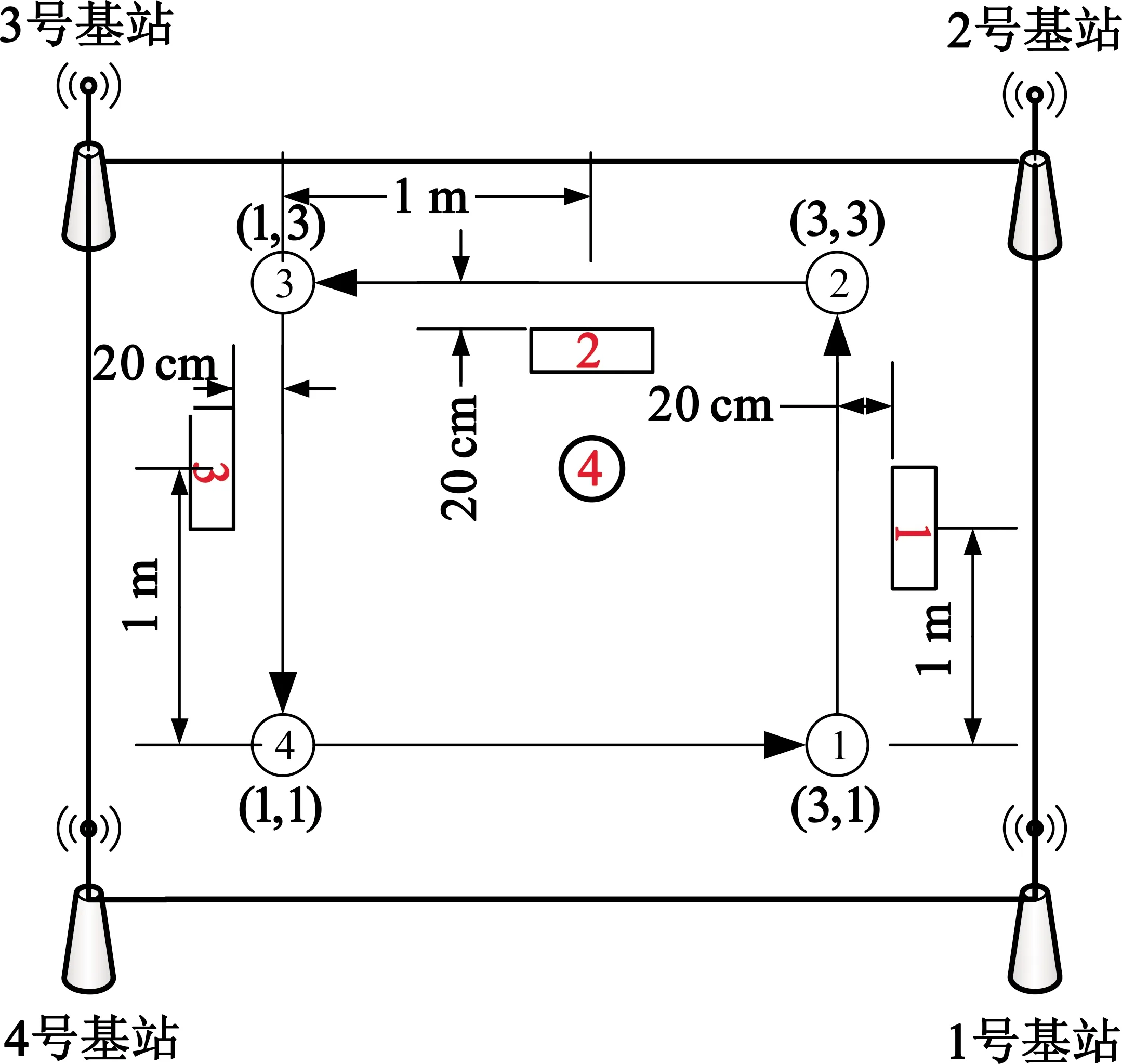
图8 障碍物实验场景示意图

图9 NLOS环境实验场景图

3.2 实验结果与分析

在障碍物数量不同的NLOS实验环境中，让机器人沿着正方形轨迹运行，采集相应的传感器信息，进行TOA定位以及LSTM联合定位。图10呈现了两种定位算法在障碍物数量不同的NLOS实验环境中的定位估计点轨迹对比结果。

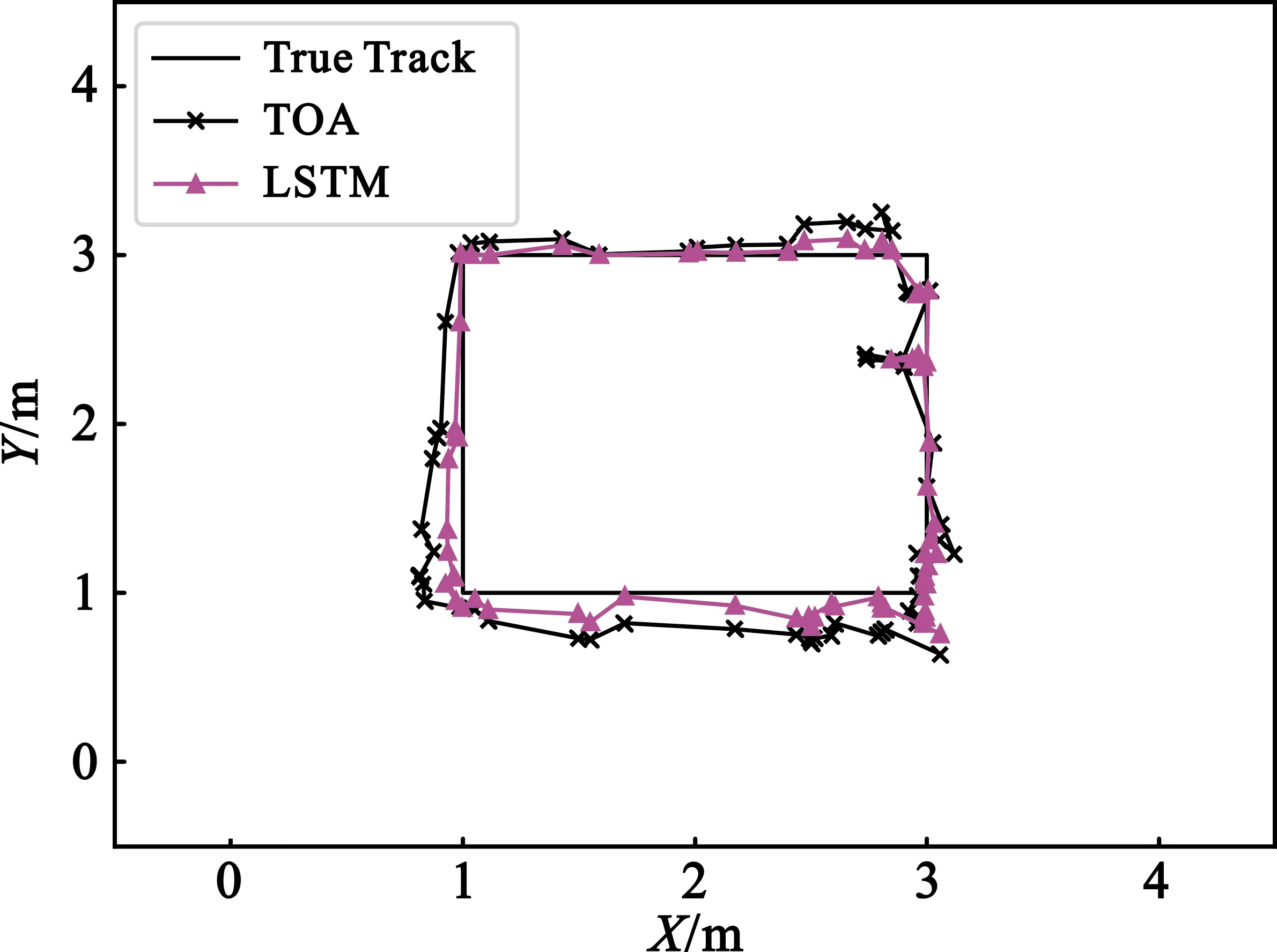
(a)单个障碍物

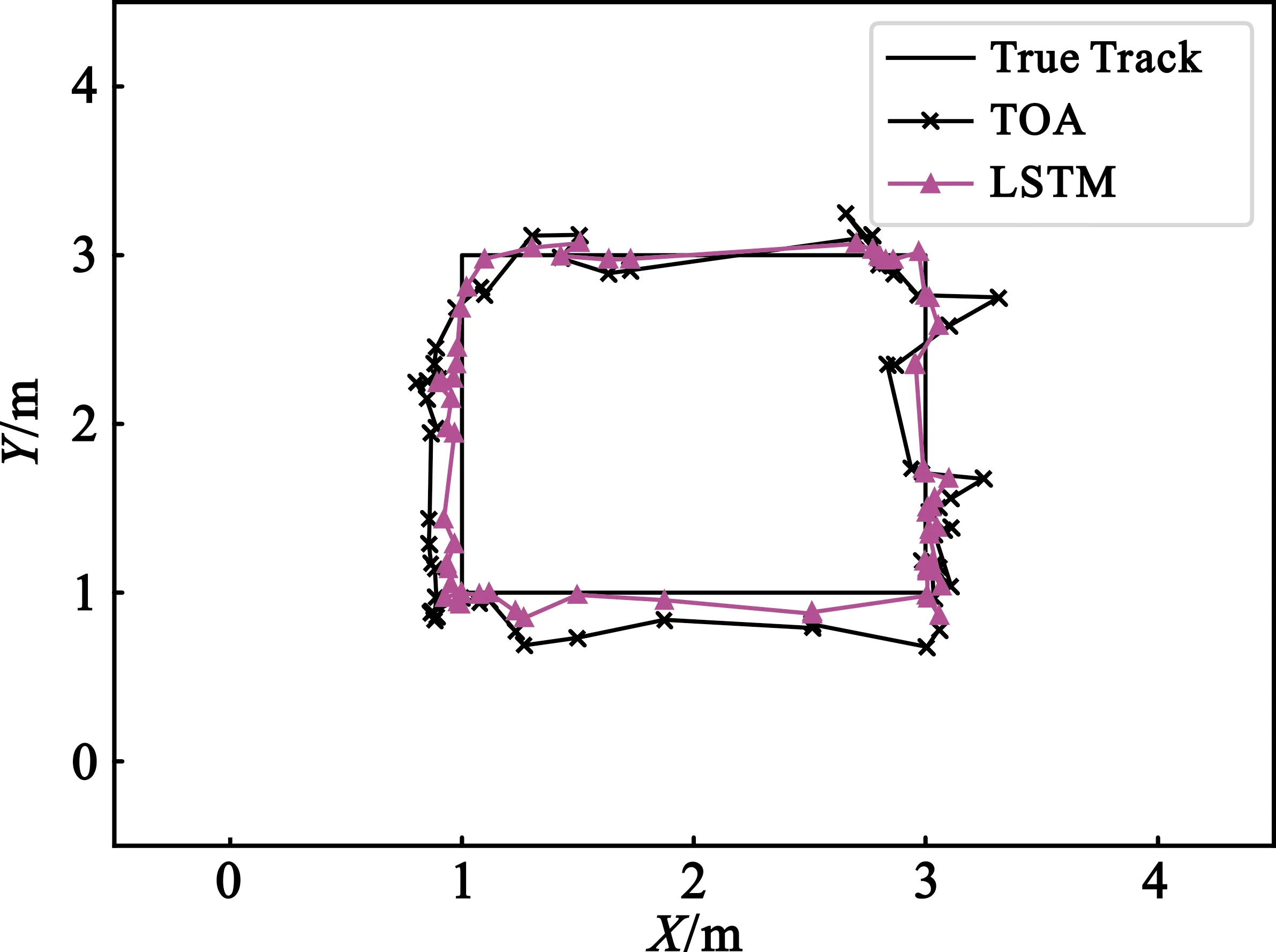
(b)2个障碍物

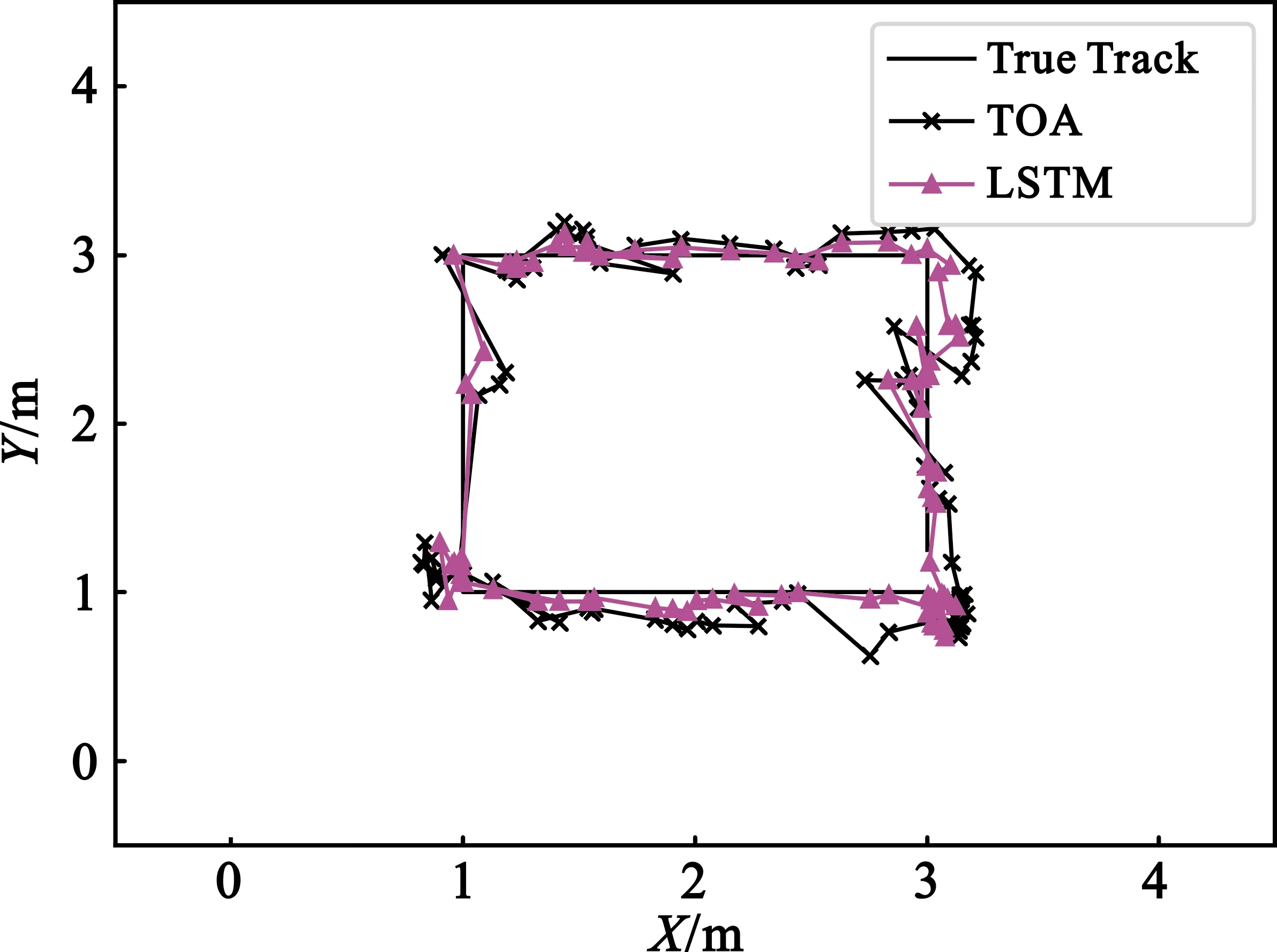
(c)3个障碍物

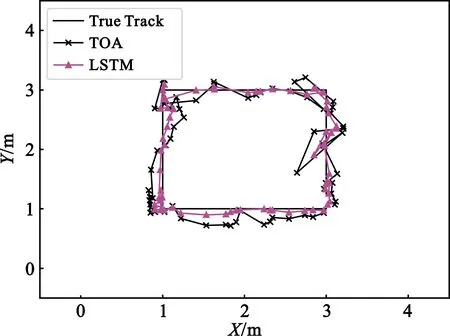
(d)4个障碍物图10 NLOS环境实验结果对比图

图10(a) 展示的是在单个障碍物的情况下两种定位算法的定位估计点轨迹对比结果，从图中可以看出，与LOS实验环境相比，定位标签处于1号障碍物附近的路径时，TOA定位精度出现了明显下降。图10(b)描述了在两个障碍物情况下的两种定位算法的定位点轨迹对比。相较于单个障碍物的情况，在两个障碍物的实验环境中，定位标签处于1号障碍物附近的路径时，TOA定位精度依旧出现了明显下降，而在2号障碍物附近的路径时，也有精度下降的情况出现。图10(c)和图10(d)分别展示了在3个障碍物和4个障碍物的实验环境中，两种定位算法的定位估计点轨迹对比结果。由图10可知，随着障碍物数量的增加，TOA定位点轨迹偏离真实轨迹的偏移值越大，也就是TOA定位精度越差。而且当标签处于离障碍物附近的位置时，即障碍物处于标签和基站之间的位置时，TOA定位精度受到的影响最大。与TOA定位算法类似，LSTM联合定位算法的定位误差变化也遵循这种趋势，但是后者定位误差受到的影响更小。与LOS环境下类似，TOA定位算法的定位误差仍旧大于LSTM联合定位算法的定位误差。

4 结束语

本文提出了适用于UWB和IMU联合定位的LSTM神经网络联合定位算法，并就该联合定位算法的总体架构设计、数据预处理过程实现、核心LSTM网络结构设计、模型训练以及相关优化方法进行了详细说明，并进行了相应仿真对比分析实验。在自行设计的实验平台上对联合定位算法在不同障碍物的非视距环境下进行了实验验证，结果表明，本文设计的联合定位算法可显著提升超宽带TOA定位精度，并且该联合定位算法的定位精度优于传统TOA、UKF联合定位算法，更加适用于当今复杂的室内定位。如果要继续深入研究本课题，可以在精度更高的硬件配合下投入商用以发现更多实际中的问题，提升整个系统性能。