有源配电网阻抗特性分析与测量

陶 骞，熊 平*，尹志鹏，孙建军，钟佩军

(1.国网湖北省电力有限公司电力科学研究院，武汉 430074；2.武汉大学电气与自动化学院，武汉 430072)

作为应对能源危机和环境污染的重要手段，基于可再生能源的分布式发电技术越来越受到人们的重视[1]。目前，并网逆变器的良好可控性以及灵活的运行模式使其成为可再生能源并网的主要接口之一，并且由于可再生能源的分布式特点，各个逆变器之间一般为并联关系[2-3]。并网逆变器通常采用脉冲宽度调制 (pulse width modulation，PWM)方式，为了抑制高频开关产生的高次谐波，通常在网侧并联LCL型滤波器或L型滤波器。但是由于分布式电源的接入，配电网本身的结构和性能受到很大的影响，同时也会影响原有的电力系统的运行、控制和保护等各方面的性能。因此，通过建立合理的有源配电网模型，研究分布式电源及其并入电网后整体的阻抗特性、并网逆变器参数对有原配电网阻抗特性曲线的影响[4-6]，具有重要意义。同时，研究测量有源配电网阻抗曲线的方法，便于工程实际中获取有源配电网的阻抗。

目前测量阻抗曲线的主要方法分为两大类：非干预式和干预式。其中，干预式测量方法是测量电网谐波阻抗的常用方法，其一般通过改变系统的运行状态获取谐波阻抗电压电流参数，从而计算谐波阻抗，主要有并联电容器投切法、晶闸管支路投切法、谐波电压/电流源注入法等，测量精度高。并联电容器投切法[7-10]，主要是通过获取投入电容器前后的电压电流暂态分量来得到电网的谐波阻抗。而晶闸管支路投切法[11]是通过改变晶闸管的导通角与导通时间得到各频率下的谐波分量，进行傅里叶分析得出谐波阻抗。文献[12]通过求取相模变换矩阵，将三相可测数据进行解耦后计算系统侧的谐波阻抗。谐波电压/电流源注入法是利用谐波电流注入电网后感应出相应的谐波电压，计算得出相应频率的谐波阻抗，由于在此方法下各次谐波频率以及幅值是可控的，在整个测量频率范围内的准确度较高，现采用谐波源注入方式实施有源配电网的阻抗测量与验证。

为此建立基于多种类型并网逆变器的有源配电网阻抗模型，并且利用闭环传递函数法将逆变器等效为诺顿模型，并通过电路变换获取有源配电网的等效阻抗，分析主电路参数以及控制参数变化对有源配电网阻抗特性影响，阐述有源配电网的阻抗测量原理，并通过MATLAB/Simulink仿真验证阻抗模型和测量方法的正确性。

1 有源配电网阻抗建模

目前有源配电网中包含大量的L型并网逆变器和LCL型并网逆变器，基于此建立了图1所示的分析模型，两类不同的并网逆变器以及负载通过可编程计算机控制器(programmable computer controller,PCC)点并联运行。LCL单相并网逆变器的具体结构如图2所示。

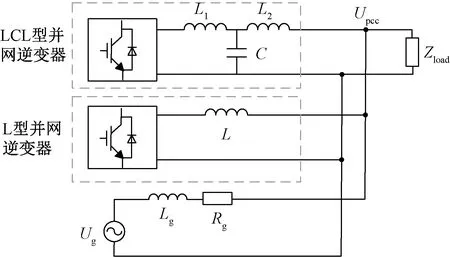
L1、L2、C分别为LCL型逆变器的逆变器侧和网侧滤波电感、滤波电容；L为L型逆变器的滤波电感；Zg为交流配电网的等效阻抗；Ug为电网等效电压源；Zload为连接在电网的负载图1 有源配电网分析模型Fig.1 Model of active distribution network

LCL型并网逆变器采用电容电流和并网电流双电流环控制，其控制框图如图3所示。根据梅森公式，图3可以进一步简化为图4。

逆变器的输入电压Udc由分布式电源提供；iL1为逆变器侧流过电感L1的电流；iC为流过滤波电容C的电流；ig1为网侧电流；PI为比例积分算法控制图2 LCL并网逆变器结构框图Fig.2 Structure of grid-connected inverter with LCL filter

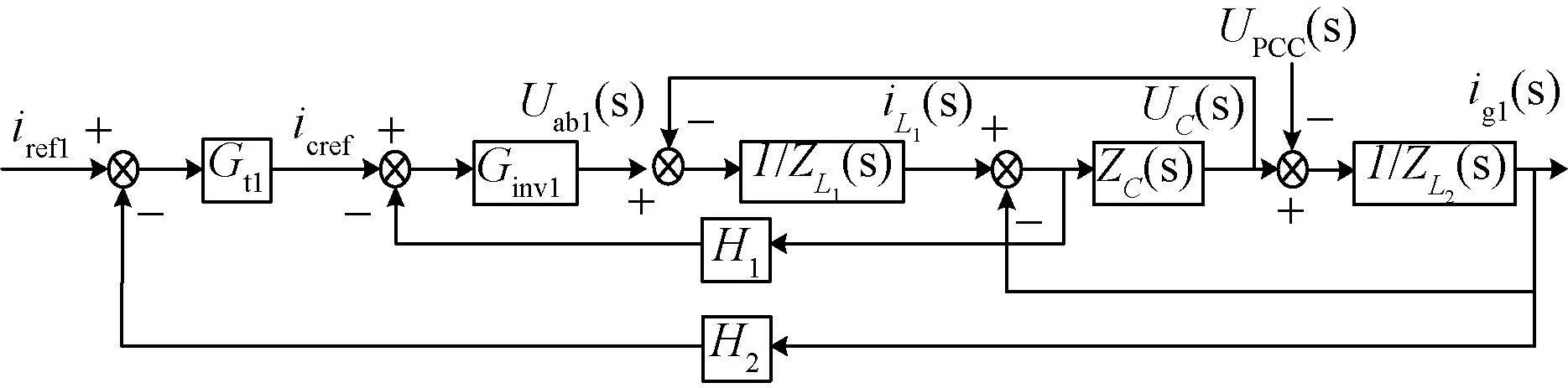
Gt为电流外环PI控制的传递函数；内环为单位增益控制；Ginv为逆变电路等效增益图3 LCL型并网逆变器双闭环电流控制框图Fig.3 Block diagram of dual-loop current control system for grid-connected inverter with LCL filter

图4 LCL型并网逆变器双闭环电流控制简化框图Fig.4 Simplified block diagram of dual-loop current system for grid-connected inverter with LCL filter

图4中，等效模块Gx1、Gx2分别满足：

(1)

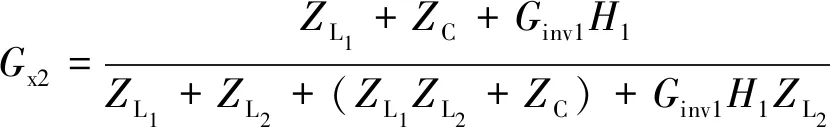
(2)

因此从图4可以推出

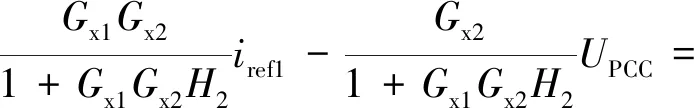
G1iref1-Y1UPCC

(3)

式(3)中：G1为受控电流源的控制系数；Y1为并联导纳。根据式(3)可以得出LCL型并网逆变器的诺顿等效电路如图5所示。

L型并网逆变器的结构框图如图6所示，ig为流过滤波电感L的电流，其控制框图如图7所示。

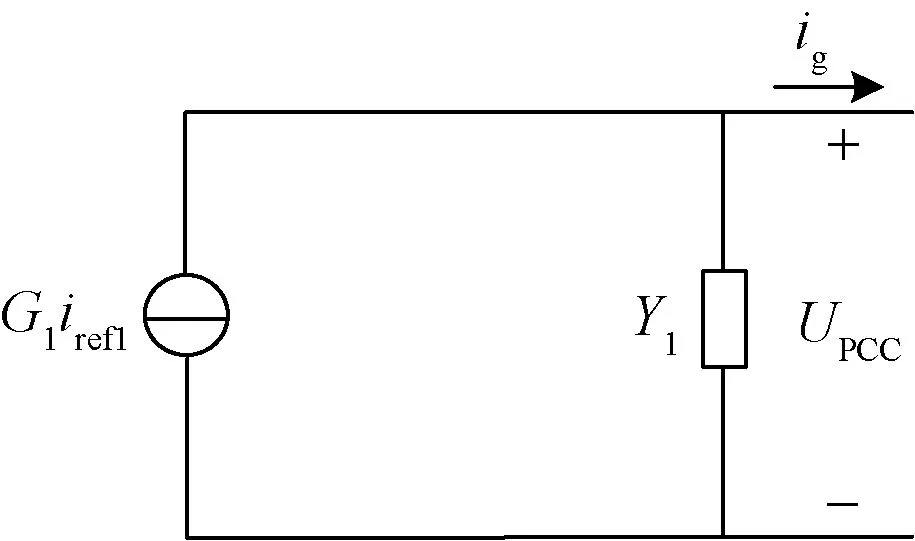
图5 LCL并网逆变器诺顿等效模型Fig.5 Norton equivalent model of grid-connected inverter with LCL filter

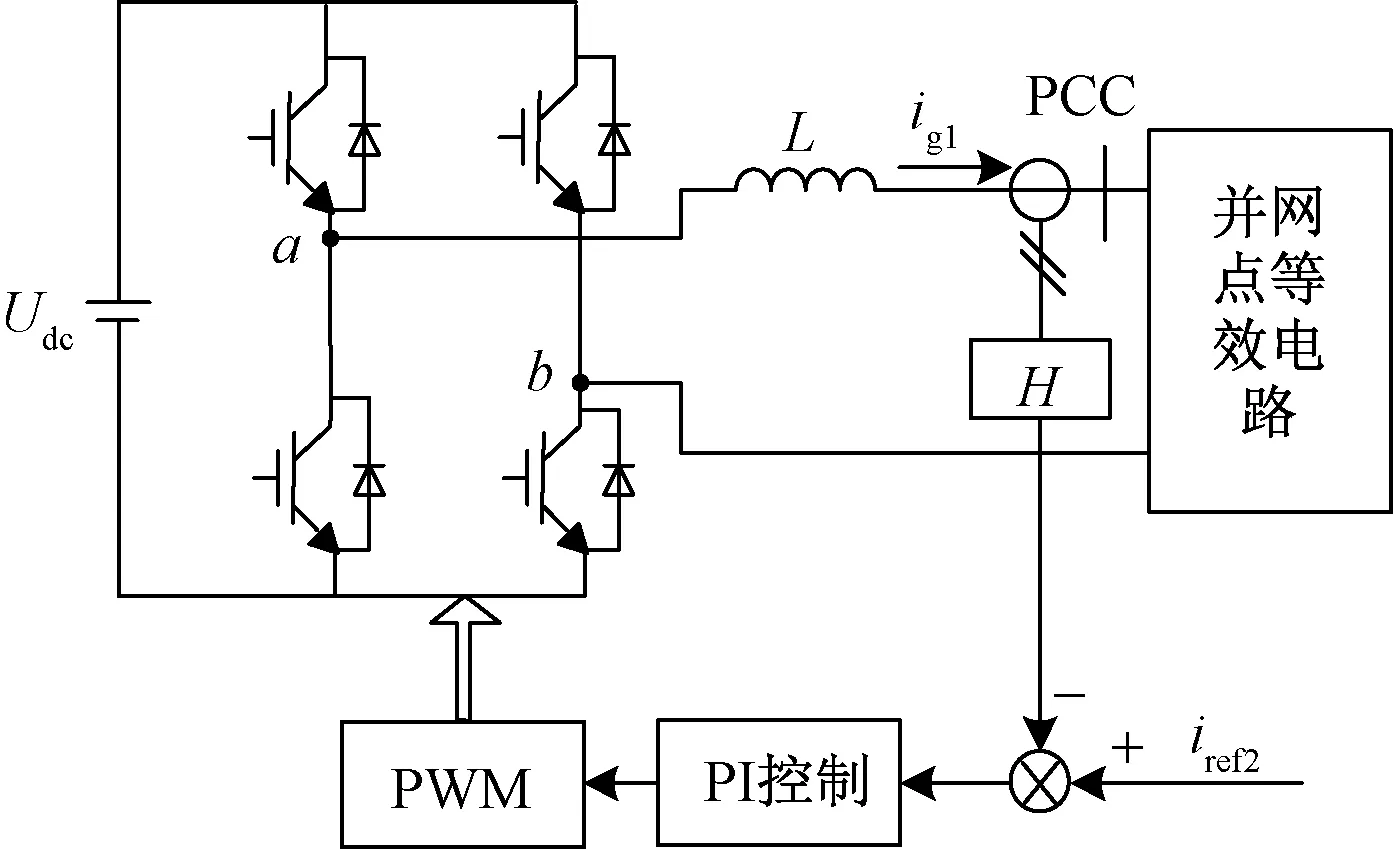
图6 L型并网逆变器结构框图Fig.6 Structure of grid-connected inverter with L filter

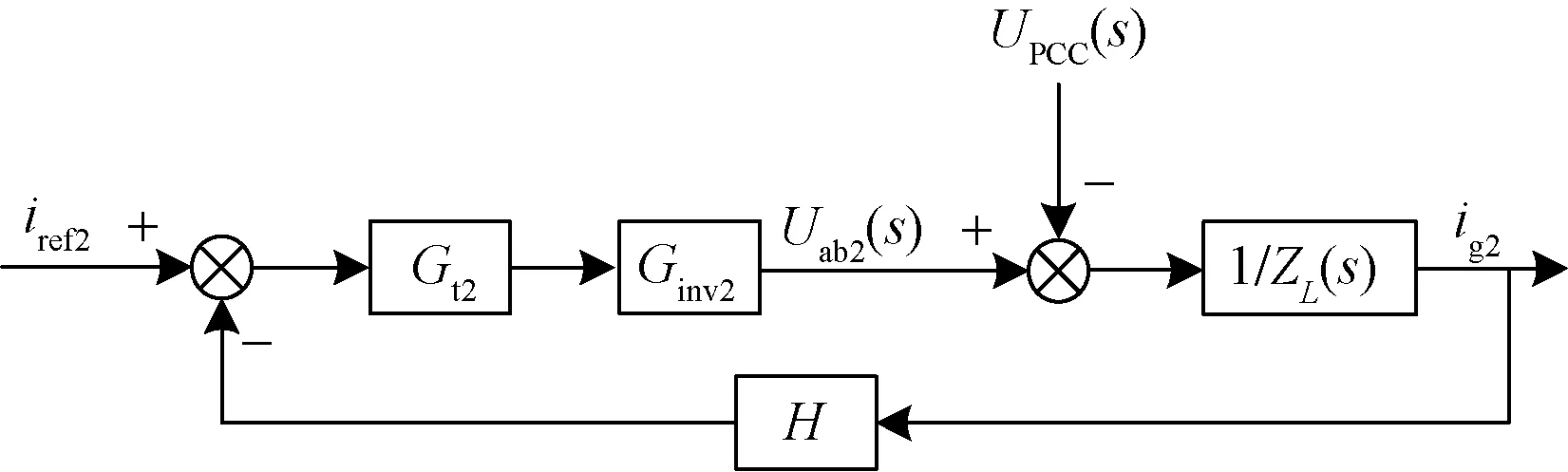
图7 L型并网逆变器控制框图Fig.7 Block diagram of control system for grid-connected inverter with L filter

由图7可得

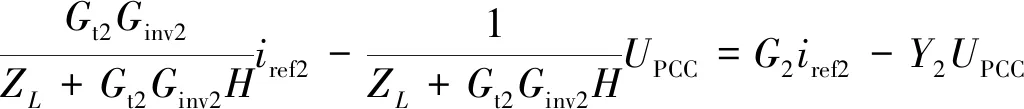
(4)

式(4)中：G2为受控电流源的控制系数；Y2为并联导纳；其等效电路与LCL型并网逆变器的类似。

因此，结合上述分析，将整个有源配电网的模型简化为如图8所示。图8进一步简化得到其如图9所示的有源配电网的电路模型，其中

ZS=1/(Y1+Y2+Yg)

(5)

通过以上的简化过程，得到了含并网逆变器的有源配电网等效输出阻抗Zs，其由逆变器的主电路参数，控制参数及电网参数共同决定。

2 逆变器参数对阻抗ZS的影响分析

为进一步研究并网逆变器参数对有源配电网阻抗的影响，如图1所示的有源配电网的模型中的电网和逆变器的主电路参数和控制参数分别如表1和表2所示。

由于电网本身的阻抗参数Lg和Rg一般是很难改变的，因此影响阻抗ZS特性的主要因素是逆变器参数，而逆变器参数主要分为主电路参数和控制参数，下面将从这两个方面进行分析。

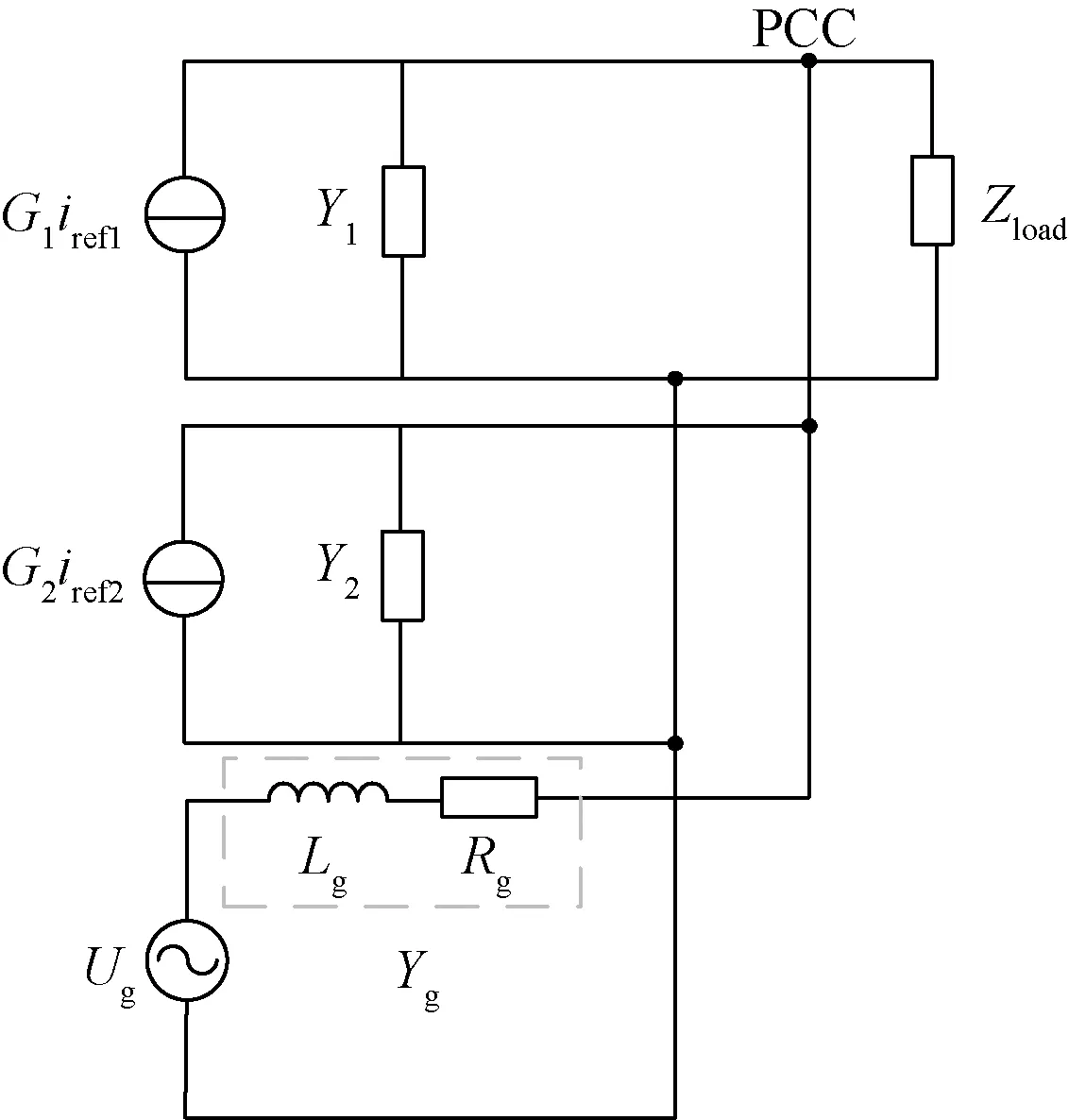
图8 有源配电网诺顿等效模型Fig.8 Norton equivalent model of active distribution network

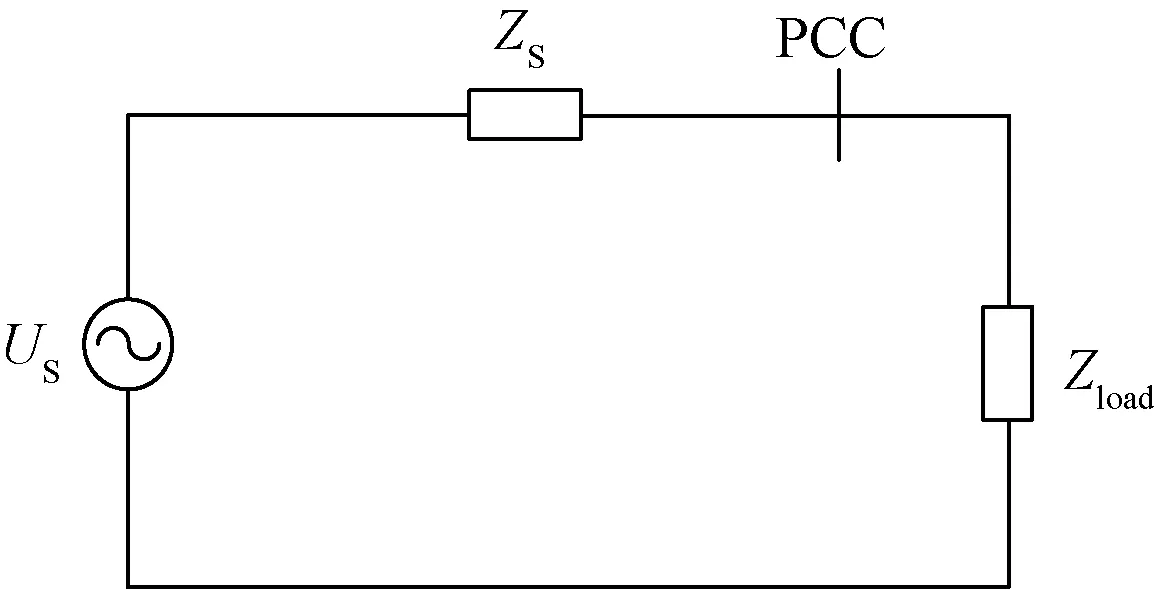
图9 有源配电网戴维南等效模型Fig.9 Thevenin equivalent model of active distribution network

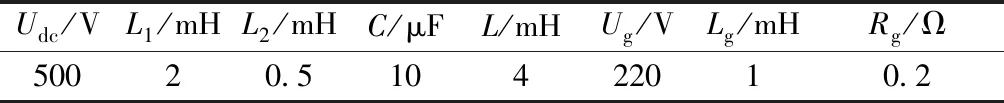
表1 有源配电网主电路的参数Table 1 Parameters of main circuit for active distribution network

表2 并网逆变器的控制参数Table 2 Parameters of control system for grid-connected inverters

2.1 逆变器主电路参数对有源配电网阻抗特性的影响

当LCL型并网逆变器和L型并网逆变器的主电路参数变化时，Y1和Y2也会随之而改变，从而影响到有源配电网阻抗ZS的频率特性。

L1取值分别为2、4、6 mH，其他参数不变时，等效阻抗ZS随频率变化的特性曲线如图10所示。

等效阻抗ZS的模值在频率<800 Hz时受电感L1的影响较小；在500～1 500 Hz时，随电感L1的增大而增大；在>1 500 Hz时，基本不受电感L1变化的影响。等效阻抗ZS的相角在频率<1 300 Hz时，随电感L1的增大而增大；在1 300～2 400 Hz时，随电感L1的增大而减小；在>2 400 Hz时，随电感L1的增大而增大。

电感L2取值分别为0.5、1、1.5 mH，而其余参数保持不变时，等效阻抗ZS随频率变化的特性曲线如图11所示。

图10 电感L1对阻抗ZS的影响Fig.10 Influence of inductor L1 on impedance ZS

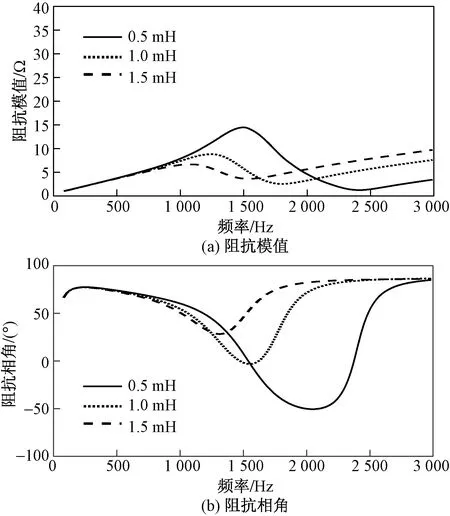
图11 电感L2对阻抗ZS的影响Fig.11 Influence of inductor L2 on impedance ZS

阻抗ZS的模值在频率<1 000 Hz时，受电感L2变化的影响极小；在1 000～1 500 Hz，随电感L2的增大而减小；在1 500～2 000 Hz时，受电感变化的影响较大；在>2 000 Hz时，随电感L2的增大而增大。阻抗ZS的相角在频率<1 500 Hz时，受电感L2变化的影响很小；在>1 500 Hz时，随电感L2的增大而增大。

滤波电容C取值分别为10、20、30 μF，而其余参数保持不变时，ZS随频率变化的特性曲线如图12所示。

图12 电容C对阻抗ZS的影响Fig.12 Influence of capacitor C on impedance ZS

阻抗ZS的模值在频率<500 Hz时受电容C变化的影响极小；在500～2 200 Hz时，随电容C变化的影响较大，在>2 200 Hz时，随电容C的增大而增大。阻抗ZS的相角在频率<600 Hz时，受电容C变化的影响极小；在500～1 700 Hz时，随电容C变化的影响很大且没有规律；在>1 700 Hz时，随电容C的增大而增大。

当L型并网逆变器的滤波电感L取值分别为4、8、12 mH，而其余参数保持不变时，ZS随频率变化的特性曲线如图13所示。

图13 电感L对阻抗ZS的影响Fig.13 Influence of inductor L on impedance ZS

在0～3 000 Hz时，阻抗ZS的模值和相角受L型并网逆变器的滤波电感L变化的影响较小。

2.2 逆变器控制参数对有源配电网阻抗特性的影响

当LCL型并网逆变器的PI控制参数KP1分别取值为0.1、0.2、0.3，而其余参数保持不变时，ZS随频率变化的特性曲线如图14所示。

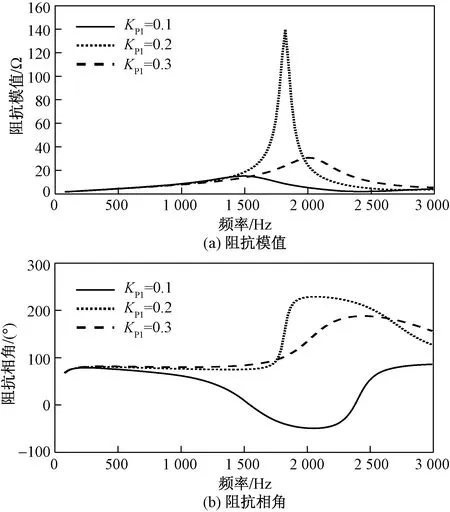
图14 控制参数KP1对阻抗ZS的影响Fig.14 Influence of control parameters KP1 on impedance ZS

阻抗ZS的模值在频率<1 500 Hz时受KP1变化的影响极小；在1 500～2 000 Hz时，随KP1的增大而先增大后减小；在>2000 Hz时，随KP1的增大而增大。阻抗ZS的相角在频率<1 800 Hz时，随KP1的增大而增大；在1 800～2 600 Hz时，随KP1的增大而先增大后减小；在>2 600 Hz时，随KP1的增大而增大。

当LCL型并网逆变器的PI控制参数KI1取值分别为100、150、200，而其余参数保持不变时，ZS随频率变化的特性曲线如图15所示。

在整个频率范围内，阻抗ZS的模值和相角受KI1变化的影响很小。

当L型并网逆变器的PI控制参数KP2取值分别为0.1、0.15、0.2，而其余参数保持不变时，ZS随频率变化的特性曲线如图16所示。

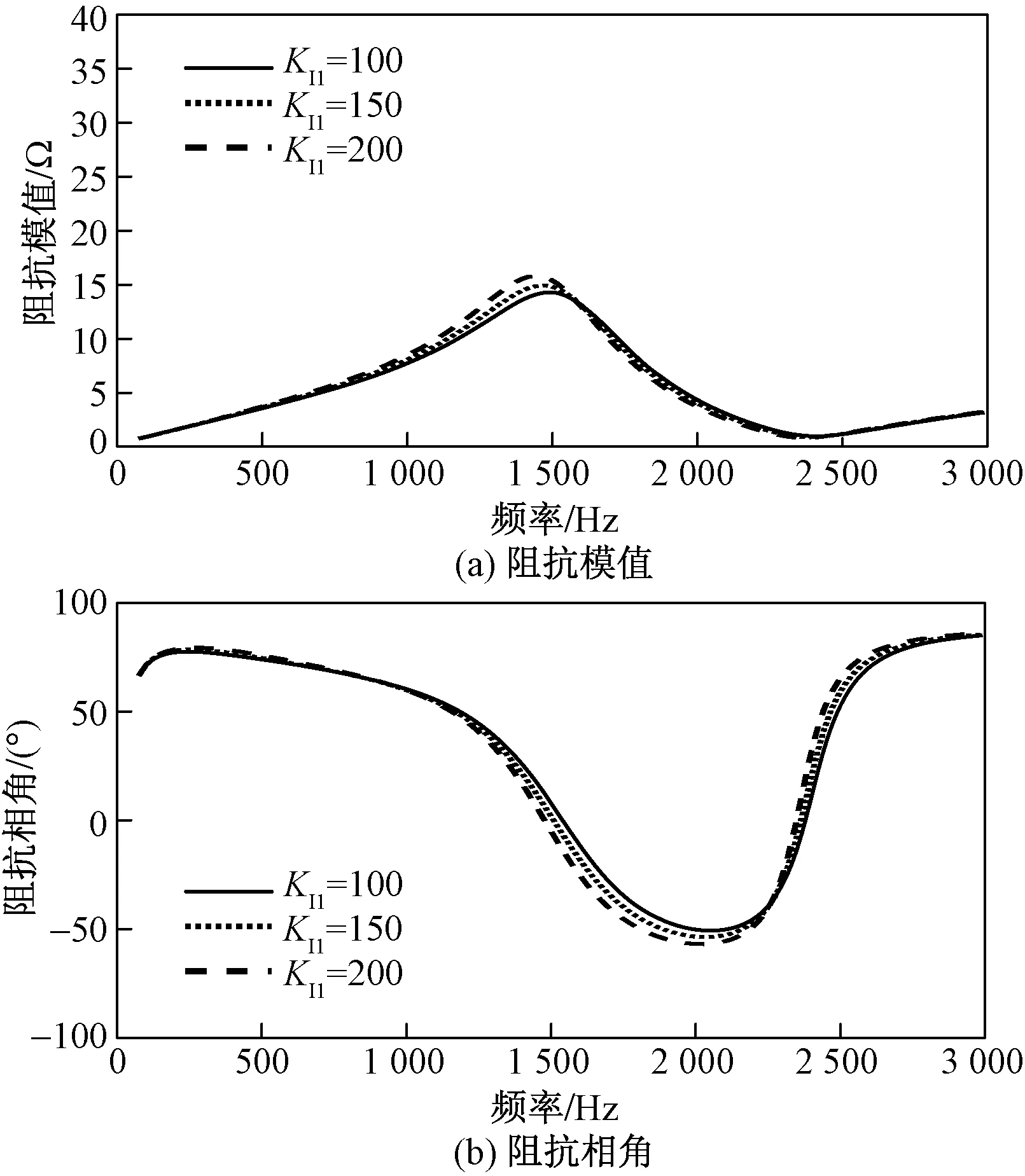
图15 控制参数KI1对阻抗ZS的影响Fig.15 Influence of control parameters KI1 on impedance ZS

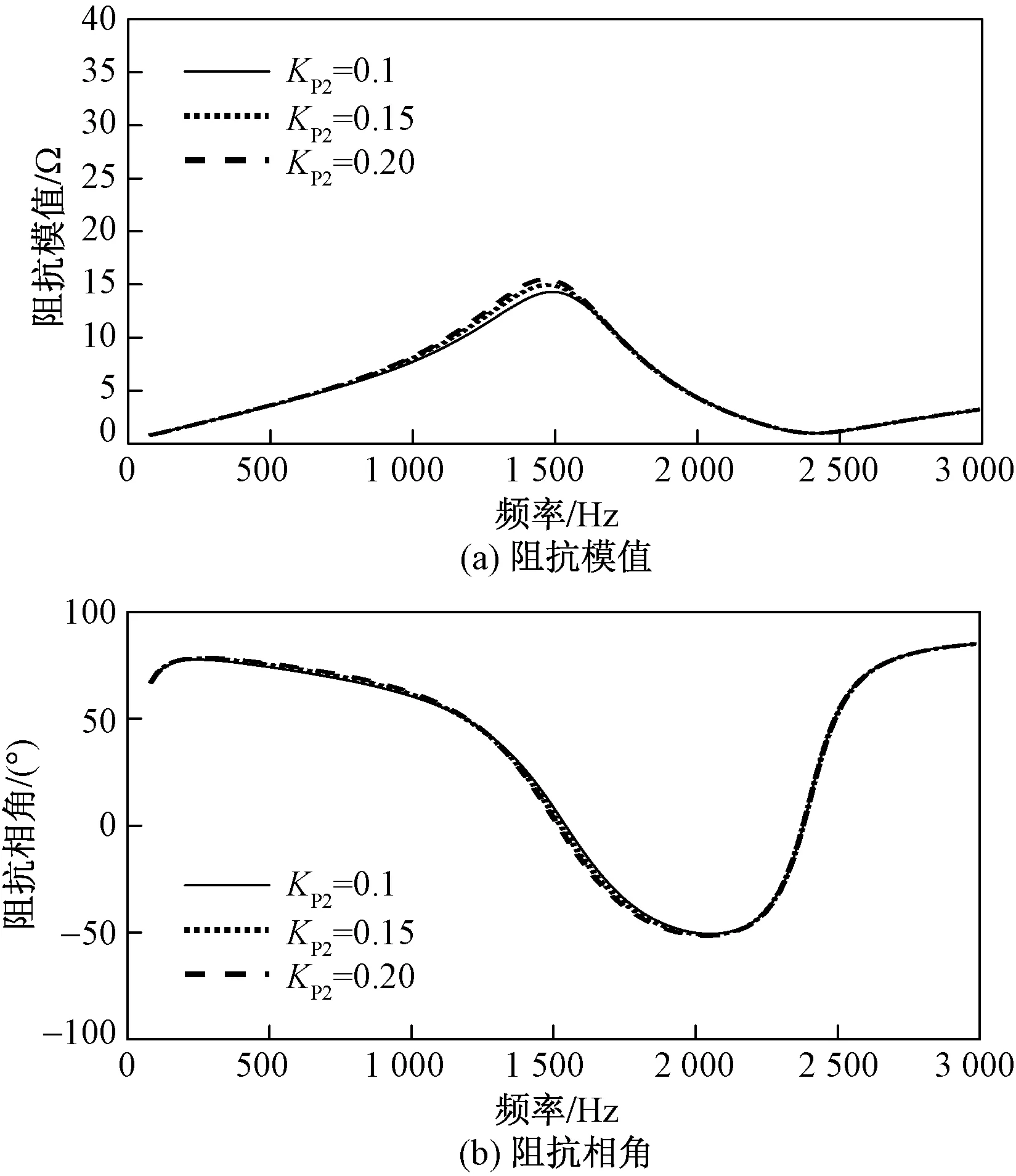
图16 控制参数KP2对阻抗ZS的影响Fig.16 Influence of control parameters KP2 on impedance ZS

在整个频率范围内，阻抗ZS的模值和相角受KP2变化的影响极小。

当L型并网逆变器的PI控制参数KI2分别取值为50、100、150，而其余参数保持不变时，ZS随频率变化的特性曲线如图17所示。

在整个频率范围内，阻抗ZS的模值和相角受参数KI2变化的影响很小。

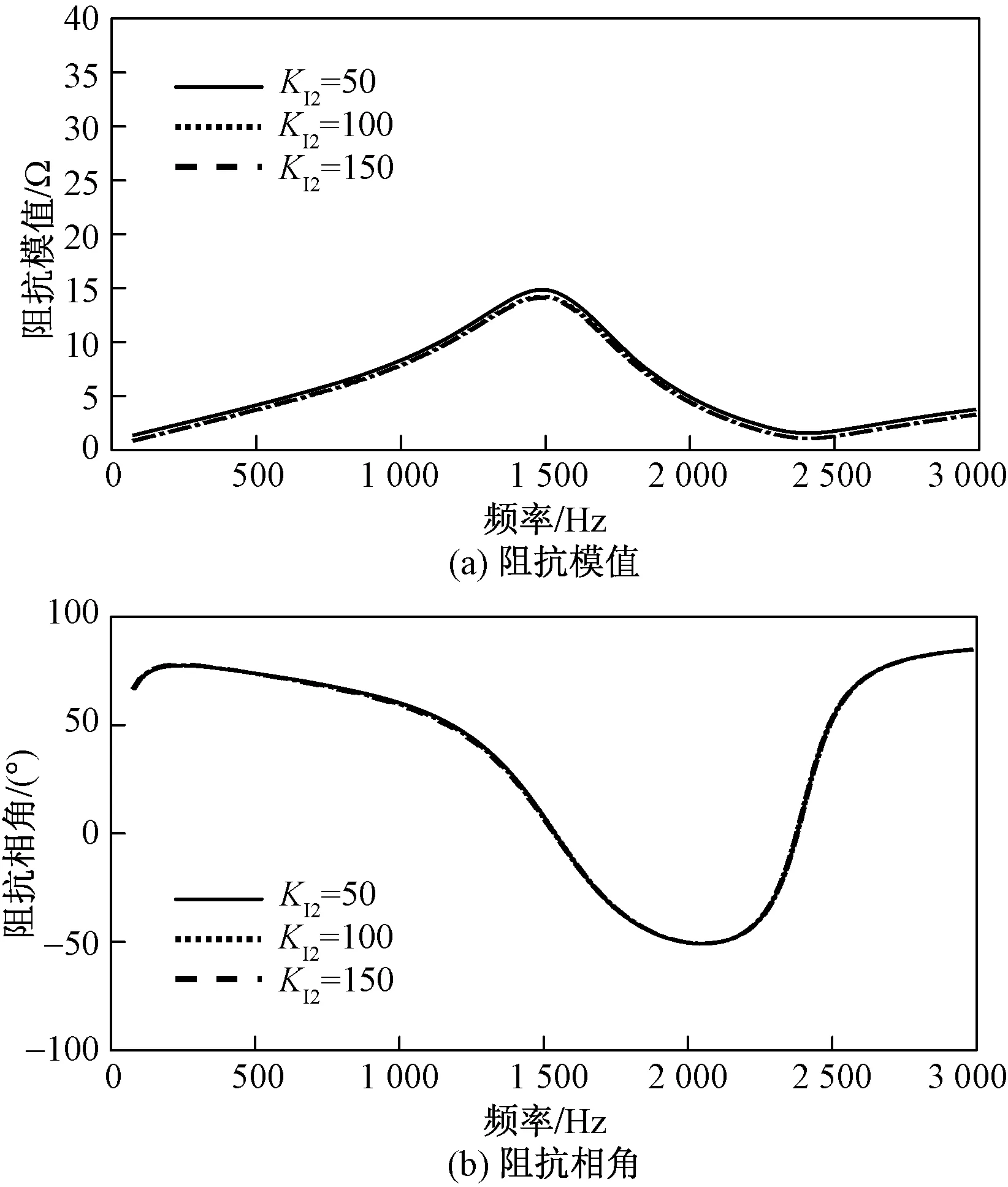
图17 控制参数KI2对阻抗ZS的影响Fig.17 Influence of control parameters KI2 on impedance ZS

3 仿真与分析

3.1 谐波阻抗测量原理

基于串联谐波电压扰动的有源配电网阻抗测量的原理如图18所示。

图18 有源配电网阻抗测量基本原理Fig.18 Basic principle of harmonic impedance measurement

其中，Um为谐波电压源，是一个电力电子电压源，其通过一个降压变压器连接到并网点，这样可以使流过电力电子装置的电流不至于过大。i1、i2分别为接入谐波电压源前后流过逆变器与电网的电流总和。接入谐波电压源之前，可以测得电流i1和电压U1；接入谐波电压源后，经过短暂的暂态过程，电路达到稳态之后，测得电流i2和U2。对得到的电压、电流进行傅里叶变换之后，得到各个频率下的分量。最后，利用接入谐波电压源前后各个频率下电压、电流的增量来计算谐波阻抗。由于在理想情况下US只含有50 Hz的分量，因此在计算其他频率的谐波阻抗时，可将其视为短路。

根据图18(a)，可以得到其拉普拉斯方程为

U(s)=US(s)+I(s)ZS(s)

(6)

式(6)中：s=jω，ω=2πf，f为系统频率。

根据接入谐波电压源前后的稳态分量计算谐波阻抗，其计算步骤如下。

首先，谐波电压源未接入系统之前，提取若干个周期的稳态电压U1、电流i1；接入谐波电压源之后，等待系统稳定，提取若干个周期的稳态电压U2、电流i2。

其次，对两种情况下的电路列写拉普拉斯方程：

(7)

最后，系统的谐波阻抗可以通过计算得

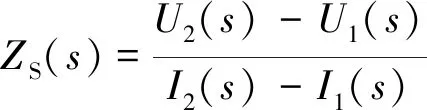
(8)

通过加入不同频率的谐波电压源，最终得出各个频率下的谐波阻抗从而得出阻抗特性曲线。

3.2 仿真验证

基于MATLAB/Simulink搭建的有源配电网仿真模型，运用谐波电压源注入法测量，得到等效阻抗ZS的特性曲线。为了避免系统的背景谐波的影响，同时降低注入的扰动电压对电网的影响，选取谐波电压源的幅值为5 V，选取谐波电压源的频率为

fk=75+50k，k=0,1,2,…,59

(9)

通过测量获取有源配电网的宽频带阻抗，进而绘制阻抗ZS的特性曲线。

仿真中LCL型逆变器的逆变器侧滤波电感的L1取值分别为2、4、6 mH，而其他参数不变时，采用谐波电压源注入法测量有源配电网阻抗，得到的不同L1值下有源配电网理论值和测量值的阻抗曲线如图19所示。

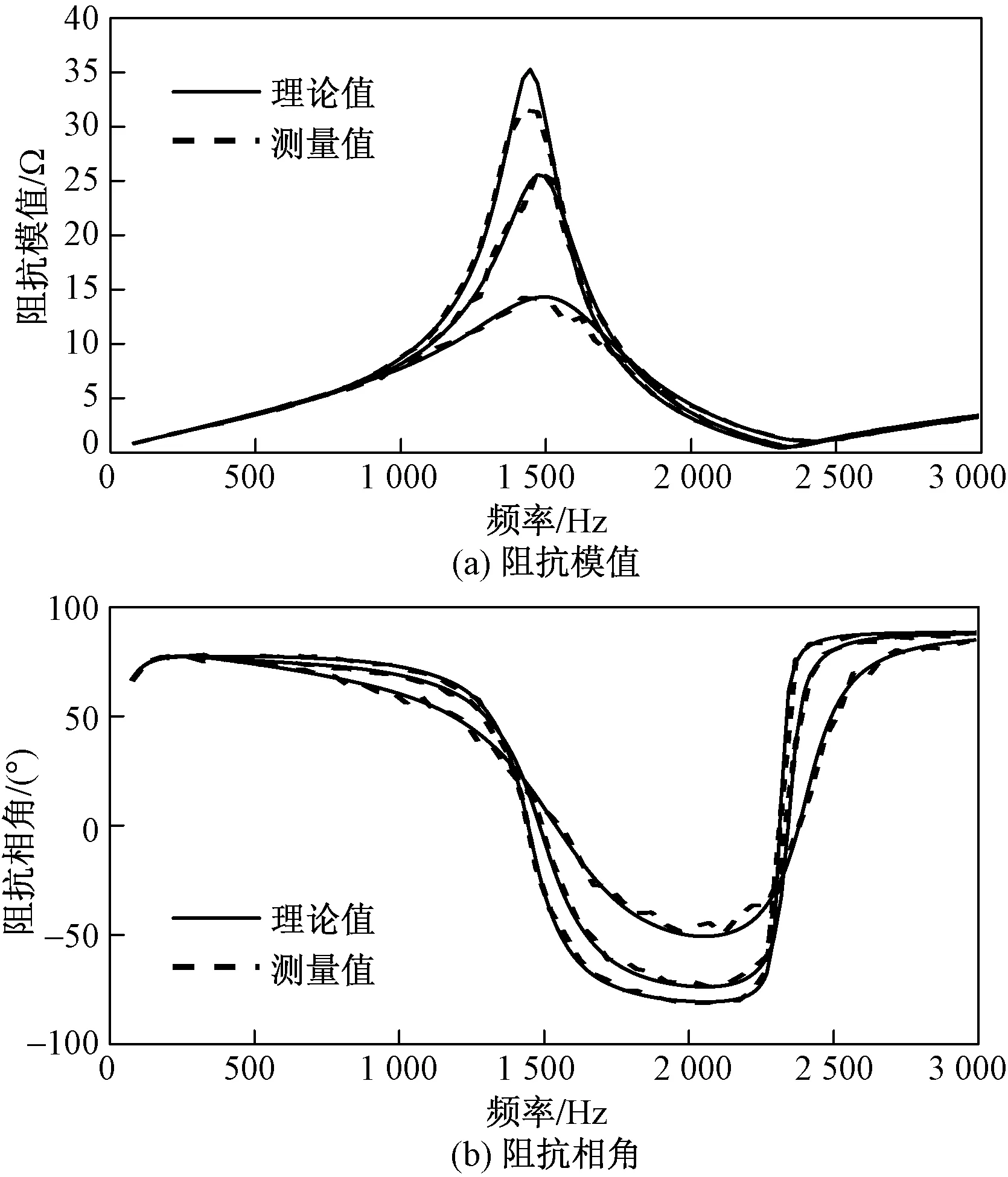
图19 阻抗ZS的测量值与理论值的比较Fig.19 Comparison between measured and theoretical values on impedance ZS

由图19可得出，谐波电压源注入法可以准确地测出等效阻抗ZS的特性曲线，并且建模值与测量值之间误差较小，证明了阻抗模型的正确性。

4 结论

建立了含有L型和LCL型并网逆变器的有源配电网的阻抗模型，分析了逆变器主电路和控制参数对有源配电网等效阻抗ZS特性的影响，并使用谐波电压源注入法对有源配电网进行了阻抗测量，得出的主要结论如下。

(1)LCL型并网的逆变器的电感L1、电感L2、电容C及控制参数KP1对阻抗ZS的模值和相角的影响较大；L型并网逆变器的电感参数L及控制参数对有源配电网阻抗影响较小。

(2)基于串联谐波电压源扰动的阻抗测量方法能够准确地测得有源配电网的阻抗曲线，验证了阻抗模型的正确性。

由于本文模型中仅考虑了单个L型和LCL型并网逆变器，因此在实际含有大量的结构和控制方式各异的并网逆变器的系统中，阻抗特性可能有所差异，但本文模型提供的阻抗特性分析思路与测量方法仍然具有重要价值。