基于GA-BP神经网络的非线性模拟量回归

周 欣，王宜怀，姚望舒，葛新越

(苏州大学计算机科学与技术学院，江苏苏州 215006)

0 引言

在嵌入式测控系统中，控制终端通过传感器对外界信息进行检测，经由放大电路、模数转换模块(analog to digital convert module，A/D转换模块)等，转换成能被终端识别的数字信号(又称为A/D值)。为便于测控系统使用，需将A/D值与实际外界信息对应，此对应过程可称之为物理量回归。

目前常见的物理量回归方法[1]有公式法，查表法，分段直线法，最小二乘法及三次样条插值法等。但受采样过程中传感器自身采样特性，放大电路与A/D转换模块转换过程中所具有的非线性变换等因素的影响，待回归A/D值与回归后的物理量之间成非线性关系。上述方法虽可用于解决物理量回归问题，但存在一定的缺陷。如公式法利用固定数字公式进行转换，速度快，但准确度不高；查表法根据输入输出表格进行查找，占用空间过大；分段直线法的分段越多，精度越高，但其复杂性也不断增加；而最小二乘法和三次样条插值法是通过采样数据确定相应的匹配函数，针对不同情况需重新确认公式，且非线性关系较为复杂，不易确定合适公式。

针对上述情况，本文提出以A/D值作为输入，传感器测量的实际模拟量作为输出，使用BP神经网络进行回归拟合。并针对BP神经网络易陷入局部极小值的问题，选择使用遗传算法进行参数优化。将遗传算法优化后的BP神经网络与最小二乘法、三次样条插值法及传统BP神经网络进行比较，实验表明，通过GA-BP算法能够有效的提高物理量回归的精度。同时提出一种回归模型在MCU端应用的方法，该方法能够较好地在MCU进行物理量回归及参数更新，具有一定的实用性和适应性。

1 GA-BP神经网络回归模型

1.1 BP神经网络

反向传播(back propagation，BP)学习算法，是一种基于误差反向传播的前向多层反馈的人工神经网络算法。通过梯度下降法，寻找实际输出值和目标值之间误差平方的极小值，从而对网络的连接权值进行调整，达到在调整过的网络模型中，对于每一组输入都能得到期望输出的目的[2]。

以A/D值作为输入，传感器测量模拟量作为输出，可构建单输入输出的神经网络模型。理论与实践表明，含有一个隐藏层的BP神经网络具有逼近任何闭区间内一个连续函数的能力[3]，因此使用3层神经网络模型进行训练和预测。其3层BP神经网络模型如图1所示。

图1 BP神经网络模型

在此网络模型中，设训练样例个数为D，网络由1个输入层单元，Q个隐藏层单元，1个输出层单元构成。

输入层仅进行数据的输入，表示为ad=X，d=1,2,3，…,D为训练样本编号。

隐藏层使用sigmoid函数作为激活函数，提供非线性变换过程，其输出为

hdi=sig(wiad+oi)

(1)

式中：wi为输入层与隐藏层之间的权值；oi为输入层与输出层的权值，i=1,2,3,…,Q为隐藏层单元数。

输出层同样使用sigmoid函数，其输出为

(2)

式中：r为隐藏层与输出层的阈值；vi为隐藏层节点与输出节点的权值,i=1,2,3,…,Q为隐藏层单元数。

1.2 遗传算法

遗传算法(genetic algorithm，GA)是一种模拟自然生存和遗传机制的最优解搜索算法[4]。通过选择、交叉和变异对种群进行多次迭代优化，选择符合当前问题的最优解，其进化过程如图2所示。

图2 遗传算法种群进化过程

该算法提供了一种求解复杂系统问题的通用框架，其全局搜索策略和优化搜索方法的计算不依赖问题的具体领域，只需要确定影响搜索方向的目标函数和适应度函数，便可以实现最优解搜索。

1.3 GA-BP神经网络算法流程

针对传统BP神经网络训练过程易陷入局部极小值的问题，使用遗传算法进行优化。将随机生成的初始权值与阈值作为种群的个体，经遗传算法筛选出较为合适的解作为BP神经网络的权值与阈值；由BP神经网络模型进行权值与阈值的进一步调整，得到能够较好反映输入输出非线性关系的训练模型，其训练过程如图3所示。

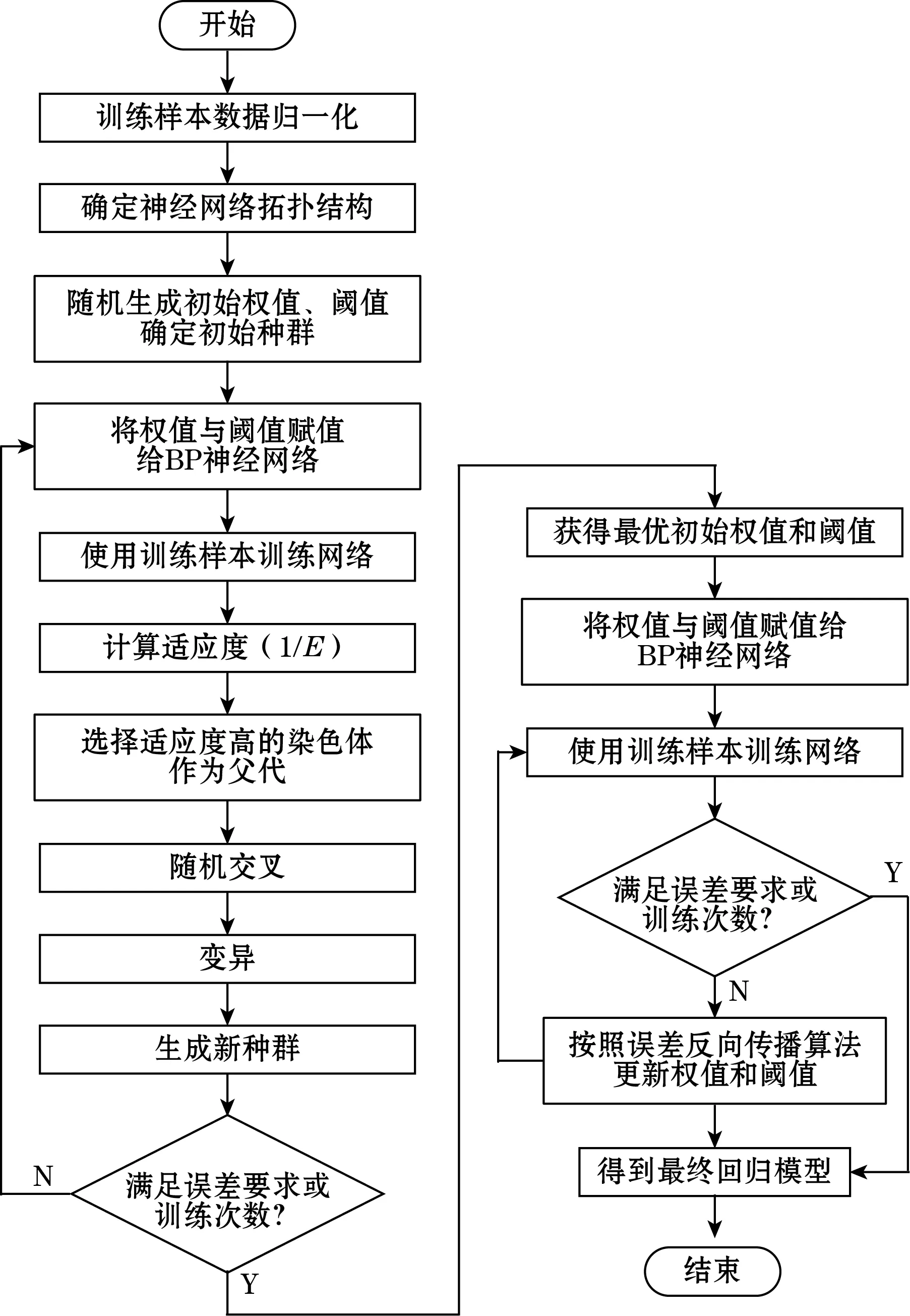
图3 GA-BP神经网络训练过程

其具体执行步骤如下：

(1)训练样本归一化。使用最大最小值归一化对训练样本进行数据压缩，保留数据特性的同时，加快训练速度。

(2)确定网络拓扑结构。根据训练样本确定隐藏层单元数、学习速率与激活函数等网络参数，生成相应的网络拓扑结构。

(3)生成初始种群。随机生成权值与阈值的初始值，并将其作为种群的个体，进行实数编码。

(4)计算适应度。适应度函数为

(3)

式中：E为遗传算法的目标函数，是BP神经网络训练后实际输出值和目标值之间误差平方和。

(5)选择父代。按适应度大小对个体进行排序，并使用赌轮盘算法[5]筛选出2个个体作为父代。

(6)随机交叉。父代以每层网络的权值与阈值作为基因，采用随机交叉算法，对基因进行组合生成新的子代。

(7)变异。生成子代中，存在一部分个体发生变异，变异概率为0.01。变异个体的权值和阈值将重新赋值，生成新的基因。

(8)是否满足停止条件。在不满足停止条件时，从原始种群中选择部分适应度高的个体与新生成子代组成新的种群，重复(4)～(7)的步骤继续求解满足情况的权值与阈值。

(9)权值与阈值的赋值。将遗传算法求解的权值与阈值赋值给BP神经网络，通过网络训练进一步实现参数的更新。

(10)权值与阈值的更新。通过网络训练比较全局误差极小值[6]来判断是否生成满足需求的权值与阈值，并使用误差反向传播方法对权值与阈值进行更新，直到满足目标训练次数或目标误差。

(11)模型生成。保存最终权值与阈值及相关参数，生成相应的回归模型。

2 GA-BP的非线性回归实验分析

2.1 数据的获取

本文针对传感器模拟量的非线性问题进行回归分析，故选择随光照强度变化，而阻值成非线性变化的光敏电阻获取训练样本。此处选用光敏电阻的型号为GM5506，其阻值随光照强度的升高而降低，使用如图4所示的采样电路，其对应电压范围为[0.55 V(亮),3.28 V(暗)]，可测得[0 lux,15 000 lux]区间内的光照强度。

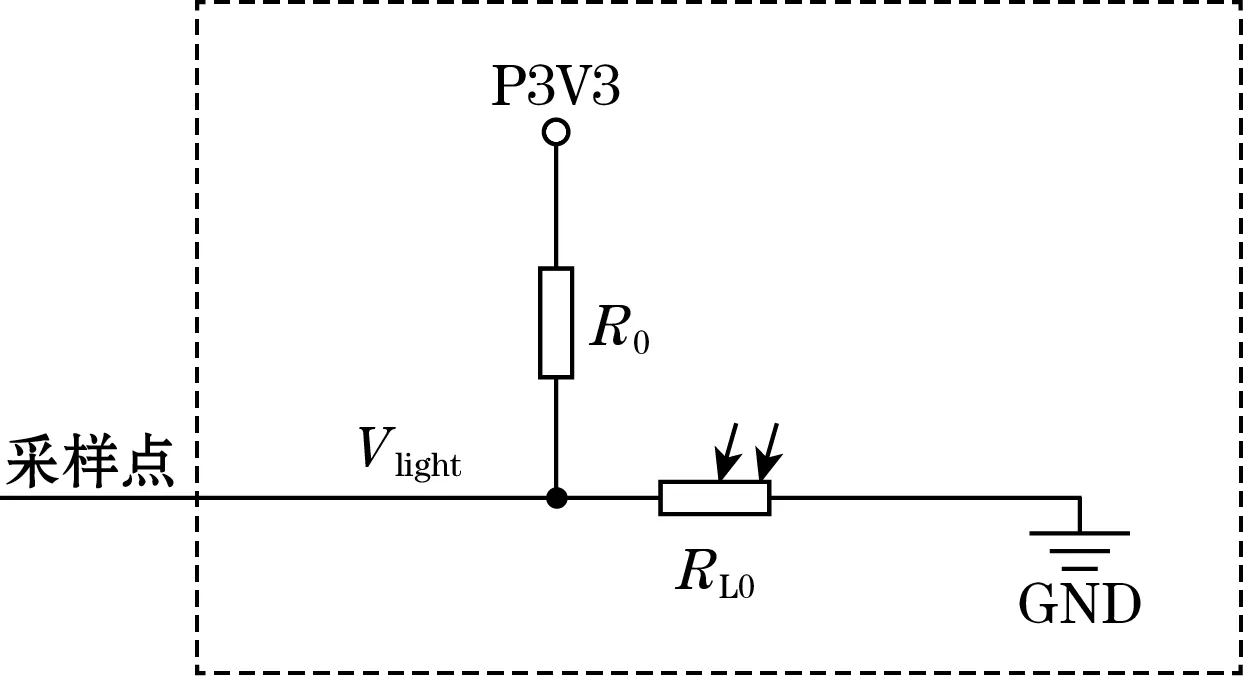
图4 光敏电阻采样电路

控制终端的16位A/D模块与采样点连接，测试获得一组光照强度和对应A/D采样值的训练样本，该训练样本数据能够较好地涵盖测量范围及其变化情况，其数据如表1所示，其中1～18为训练数据，19～26为测试数据。

表1 训练样本——光照强度与A/D值样本

2.2 评价指标

为了对不同方法进行比较，引入均方根误差与决定系数对预测效果进行评判。均方根误差(root mean squared error，RMSE)计算观测值与真实值之间的偏差，其值越小，预测效果越好。

(4)

式中：o为观测值；t为真实值。

决定系数又称为拟合优度，通常使用R表示，反映的是回归的拟合程度，其值越大，拟合程度越好，预测性能也就越优。

(5)

2.3 实验方案与结果

本文实验模型使用C#语言编程实现，具有训练与验证功能。通过对模型的分析可知，其输入与输出神经元个数均为1。采用sigmoid型函数作为激活函数的神经网络具有对任意连续函数的逼近能力[7]，故选取sigmoid函数作为激活函数，使用梯度下降法进行权值与阈值的更新。隐藏层单元个数的范围可依据经验公式[8]计算得出:

(6)

式中：q为隐藏层单元数；p为输入层单元数；m为输出层单元数；α为1～10之间的常数。

对于回归模型，其隐藏层单元数范围在3～11之间。经多次实验验证得出隐藏层单元数为8时，具有更好的拟合效果。设定学习速率为0.1，目标误差精度为0.000 001，初始权值和阈值随机生成。

在此网络结构基础上，使用遗传算法对初始权值与阈值进行优化，初始种群大小为100，变异概率为0.01，迭代次数为1 000。

在上述网络中，使用样本中的训练数据进行训练，得到对应的权值与阈值参数如表2所示。

表2 BP神经网络各层参数

权值与阈值以及网络相关参数共同构成一个GA-BP网络模型。使用该网络模型对测试数据进行验证分析，由表3可以看出，光照强度的预测值与实际值误差基本能控制在可接受范围以内。

表3 测试样例输出测试

2.4 方法对比

2.4.1 传统方法与神经网络的对比

传统的非线性回归方法有最小二乘法和三次样条插值法。最小二乘法通过最小化误差平方和找寻最佳函数匹配[9]，三次样条插值法通过三弯矩法并结合边界条件推导系数方程确定对应的回归函数[10]，实际是在相邻数据点之间确定一个三次样条函数。

针对本文使用的训练样本，使用最小二乘法和三次样条插值法进行回归拟合，并使用测试样例与BP神经网络进行验证对比，图5给出各方法的预测结果的回归曲线，并列出各方法的均方根误差和决定系数，如表4所示。

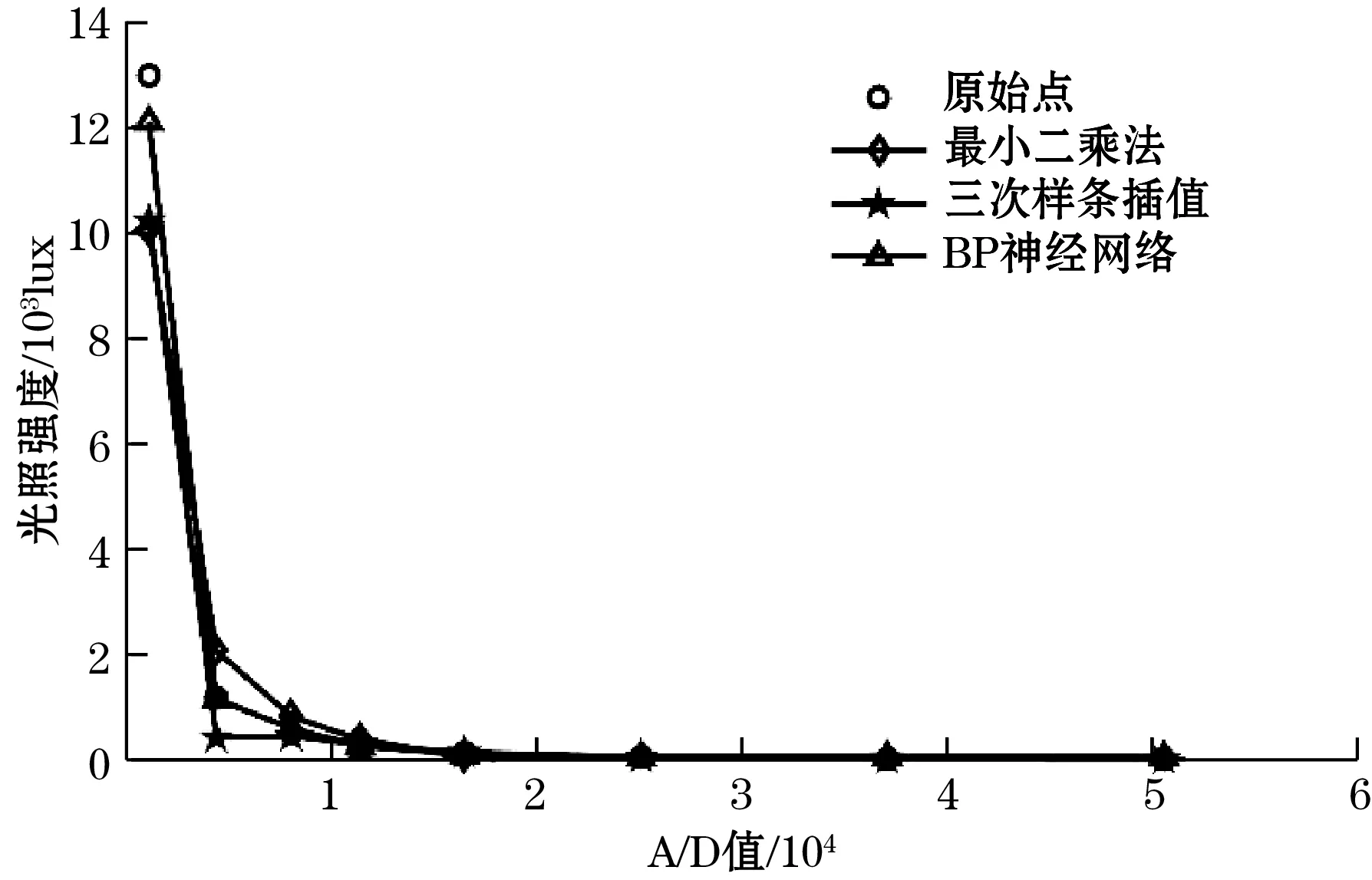
图5 光照强度与A/D值的物理量回归曲线

表4 传统方法与神经网络的对比

综合图5和表4可以看出BP神经网络的预测准确度优于其余2种方法。最小二乘法与三次样条插值法的拟合是确定具体公式及其系数，BP神经网络确定网络相关参数。3种方法在回归形式上存在一定的区别，但都可转换为使用一定的回归公式进行回归预测。不同在于对不同的训练样本，最小二乘法与三次样条插值法需要重新确认公式，而BP神经网络模型的回归公式可不改变，仅需校正权值与阈值。同时BP神经网络可以通过不断提升训练次数来减小误差，达到更好的拟合效果，是一种具有较好拟合能力的非线性回归方法。

2.4.2 BP神经网络优化对比

由上述对比实验可知，BP神经网络对于传感器模拟量的非线性回归问题具有较好的拟合能力。但BP神经网络存在易陷入局部极小值的特点，针对此问题使用遗传算法进行优化。分别记录下BP神经网络与GA-BP神经网络训练过程中每10 000次训练实际值与目标值之间的误差平方和，绘制成如图6所示的曲线。并计算相应的均方根误差和决定系数，如表5所示。

图6 GA-BP与BP误差状态

表5 GA-BP与BP对比

从图6可以看出，GA-BP神经网络模型在训练过程中的收敛速度明显优于传统BP神经网络。同时结合表5可以看出，在训练相同次数的情况下对GA-BP的拟合程度优于传统BP算法，具有更好的预测准确度。

3 BP神经网络在MCU上的应用

模型训练过程在PC端完成，而生成的网络模型则应用于MCU端。图7为训练模型在MCU端的应用过程。

图7 神经网络在MCU端应用

针对上述流程，将BP神经网络在MCU端回归预测功能封装成构件，构件中各函数及功能如表6所示。

按图8所示的结构类型将网络参数存储在固定Flash区域；芯片启动后，使用BPinit函数读取位于Flash区域的存储参数，构建神经网络模型；实时使用A/D转换模块读取传感器A/D采样值后，利用BPpredict函数进行转换到传感器的实际输出值；同时包含参数更新功能，当计算结果存在误差时，可重新采集训练样本在PC端训练，并将训练结果利用BPUpdate函数将网络模型重新写入相应Flash区域。

以MKL36Z64[11](简称KL36)芯片和S32K144[12](简称S32K)芯片为例进行MCU端预测实验。KL36属于ARM Cortex-M0+内核，其对应的Flash为64 KB，RAM大小为8 KB；而S32K属于ARM Cortex-M4内核，其对应的Flash为512 KB，RAM大小为60 KB；其内置A/D转换模块精度均为16位。使用该构件进行光照强度的采样与回归，在KL36与S32K上均能按照如图7所示的流程进行回归预测。

表6 BP神经网络预测构件

图8 网络参数存储结构体

4 结束语

本文针对非线性传感器A/D值与模拟量之间存在的非线性关系难以确定回归公式进行表达的问题，提出使用BP神经网络对传感器A/D值与模拟量进行回归拟合。实验表明，使用BP神经网络能够对两者之间的非线性关系进行良好表达，和最小二乘法与三次样条插值法相比，BP神经网络的拟合程度明显优于其余2种方法，具有较高的准确度，并能有效提升转换后的精度。而使用遗传算法优化后的GA-BP神经网络，能加快BP神经网络的收敛速度，回归的精度也进一步提升。同时提出一种在MCU端应用的方法，网络参数固化至MCU端存储，并利用BP神经网络构件实现在MCU的回归预测，具有一定的实用性和适应性。