基于分数阶非线性各向异性扩散的图像去雾算法

吴 绪 玲

(西南交通大学希望学院信息工程系 四川 成都 610400)

0 引 言

随着户外计算机视觉系统在城市交通、自主导航和遥感探测等方面的应用越来越多，人们对监控系统拍摄出来的图像清晰度的要求也越来越高[1]。但是，在真实情况下获取的图像可能会受到恶劣天气、雾或霾等条件的影响，出现大量细节信息丢失的现象，影响后期图像特征的提取[2]。作为计算机视觉系统的输入源，图像质量会对整个系统的性能产生直接影响。因此，国内外研究人员创建许多图像去雾算法来降低这种影响。

目前，图像去雾技术[3]大致可以分成两类。一类是不考虑图像降质原因,采取常规图像增强算法如对比度增强[4]、直方图均衡化[5]、基于Retinex理论的图像增强[6]作为基础处理手段的非物理模型图像去雾技术，这类方法通过提高图像对比度降低雾或霾对图像的影响，但是也容易造成过增强或者信息损失现象；另一类是考虑图像雾天降质原因，利用大气散射原理复原真实场景的物理模型图像去雾技术，如暗通道先验方法[7]，这类方法畸变较小，去雾效果很好，但是计算复杂度较高。基于偏微分方程的各向异性扩散方法[8]是一种基于物理模型的图像去雾算法，该方法通过对有雾图像的多次迭代处理获得较好的去噪效果。Nnolim[9]提出一种基于偏微分方程(PDE)的模糊图像对比度增强算法，在适当的PDE框架中采用倒对数反射和梯度优化对图像进行多尺度局部增强。Bai等[10]提出一类广义各向异性扩散方程用于图像去噪，首先对图像强度函数G-导数进行傅里叶变换，然后将其引入广义各向异性扩散方程，并利用G-导数算子的半群性质进行图像去噪。Pushparaj等[11]提出一种基于局部灰度级的对数正态分布的各向异性扩散的全色图像方法，利用扩散系数函数中的自适应阈值参数，自适应地调整了特征空间的低边缘梯度对噪声图像去噪和平滑的影响，在保留了全色图像特征的同时，有效地去除了图像中的噪声。Yin等[12]提出了一种基于分数阶差分曲率的分数阶各向异性扩散方程，利用傅里叶变换引入分数阶导数的频域定义，用于表征图像中强度的变化，使得新的边缘指示器更好地处理精细纹理。

针对大多数各向异性扩散方程在去雾过程中容易模糊边缘细节的问题，本文提出一种基于分数阶非线性各向异性扩散的去雾算法。使用从模糊图像中提取的大气光作为各向异性扩散过程中的初始值，然后通过迭代扩散过程计算精细的大气光传输图，能够有效地突出去雾图像的细节，而且在空间域中执行迭代过程使得算法在计算方面能够简单快速的实现。

1 分数阶非线性各向异性扩散模型

1.1 分数阶导数

(1)

式中:α,μ∈R且α,μ≠1；ξ表示积分变量；Γ(·)表示伽马函数。当μ=0时，上述积分可转换为经典的黎曼-刘维尔分数积分。本文将利用这个分数积分定义黎曼-刘维尔分数导数。类似于广义分数积分，α阶广义微分算子可以定义为：

(2)

(3)

式中：0≤α<1。

偏分数阶导数的x与y分量分别由初始大气光传输图与固定小尺度矩阵A和B的卷积计算得到，其中小尺度矩阵A和B表示为：

(4)

随着迭代次数的增加，导数将根据大气光传输图中的精细化程序进行微调，卷积方法返回卷积层的中心部分与大气光传输图的尺寸相同。

1.2 各向异性扩散

Perona等[13]提出了基于热扩散方程的各向异性扩散方程，用于对图像进行平滑去噪。该模型克服了低通滤波方法在各向同性方向上平滑图像的缺点，根据像素的分布情况有选择地进行各向异性扩散。各向异性扩散模型是一种线性热扩散方程的推广，其椭圆型偏微分方程可以表达为：

(5)

在非线性各向异性扩散中，扩散张量D根据滤波后的图像u来定义：

(6)

Du(x,t)=cu(x,t)Id

(7)

(8)

2 算法设计

2.1 雾天成像模型

由Koschmieder准则[14]，雾天成像模型通常可以表示为：

I(x,y)=I0(x,y)e-kd(x,y)+I∞(1-e-kd(x,y))

(9)

式中：I0(x,y)和I(x,y)分别表示为无雾图像和有雾图像在像素(x,y)处的强度；k是与大气相关的散射系数；d(x,y)是场景与相机的距离；I∞表示大气光或者天空强度；e-kd(x,y)表示透射率图，一般由t(x,y)表示。在无雾图像时，k≈0；但是在模糊图像中，k≠0是不可忽略的量。因此，式(9)中的第一项表示直接衰减量，使得场景辐射在介质中发生衰减，对比度降低；第二项表示大气光传输图A(x,y)，场景颜色通常会因为大气光传输图的发散而发生变化。

通过将天空强度取为1，模糊图像标准化后模型表示为：

I(x,y)=I0(x,y)(1-A(x,y))+A(x,y)

(10)

可以看出，为了将模糊图像恢复至无雾图像，需要精确估计A(x,y)。

2.2 去雾算法实现

平滑是图像恢复和增强的一种重要的技术手段，但是传统的平滑滤波方法容易造成图像纹理和边缘细节的丢失。为了避免滤波过程中的图像细节的损失，本文采用基于分数阶导数的各向异性扩散理论自适应地估计大气光传输图A(x,y)。该方法既克服了纯各向异性扩散方程在平滑区域因过度扩散导致的阶梯效应，也避免了整数阶PED模型在去噪方面效率低的问题，而且分数阶模型能够通过平滑程度和平滑方向来稳健地控制平滑效果。

设c是扩散常数，t表示时间，各向异性扩散表示为：

(11)

与式(11)相关的能量函数为：

(12)

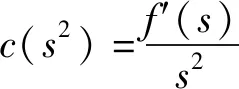
(13)

对于欧拉-拉格朗日方程的最小值问题，可由下列方程计算得到：

对于任意函数η，假定：

(14)

则：

(15)

(16)

当α=1时，式(16)为标准Pietro-Malik模型，α=2为四阶各向异性扩散模型，本文采用分数阶扩散模型，即1<α<2。

式(16)可以根据梯度下降法求解：

(17)

初始条件为A(x,y)，t→∞时获得最终解。但是，在数值求解的过程中，一般选择在去雾和边缘细节完好保存两者之间的最佳折衷时停止迭代。

对于实际模糊图像，首先假设初始离散图像A的像素尺度为m×m，像素从(0,0)开始，以均匀间隔Δx=1和Δy=1进行采样。

假定K1、K2是空间域中的纯对角运算符，定义为：

(18)

(19)

(20)

(21)

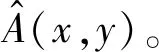
(22)

(23)

因此，提出的去雾算法估计大气光传输图的伪码如算法1所示。

算法1基于空间域分数阶导数的各向异性扩散

输入：初始大气光传输图A(x,y)，最大迭代次数nmax，α和Δt=4-α。

1.n=0时，输入u0=A(x,y)，nmax，t=kΔt

forn=0,1,…,nmax,do

3. 计算hxn、hyn；

5. 计算un+1=un-gn×Δt；

End for

6. 返回A(x,y)=un。

(24)

式中：c∈(r,g,b)。上述方法也适用于灰度图像，唯一不同的地方是初始的大气光传输图。

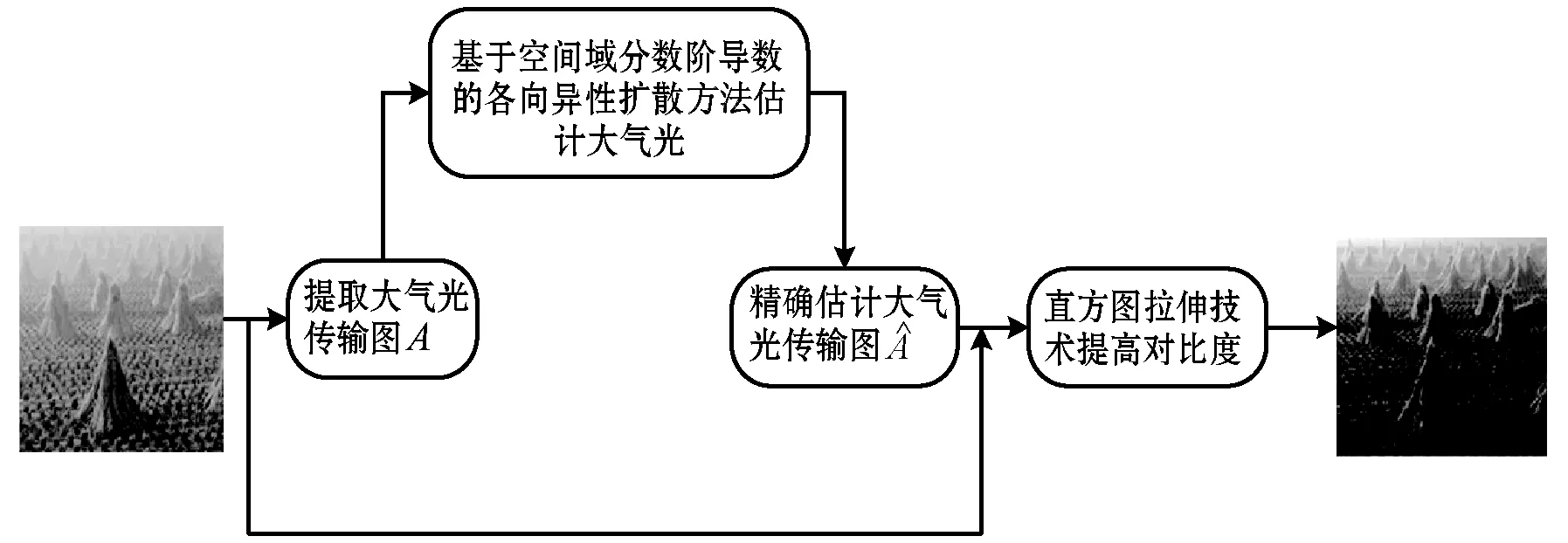
图1 本文去雾算法流程

3 实 验

所有实验在一台配置为CPU Intel Core i7-4700 MQ-2.4 GHz@6 GB RAM的机器上执行，所有测试均在MATLAB 2017a环境下实现。选取数字图像处理常用的七幅图像，即Forest、Wheat、Tomb、Ny17、Swan、N6和Train作为验证算法的测试图像。这些图像具有不同的纹理细节，并且图像中含雾量也有所不同，像素尺寸为256×256。在本文研究中，分数阶参数α取1.8较为合适。将测试结果与基于高斯过程回归(GPR)去噪算法[2]、基于偏微分方程(PDE)去噪算法[9]、广义各向异性扩散方程(GAD)去噪算法[10]和基于核回归模型(KRM)去噪算法[15]。

3.1 主观分析

图2-图3给出了几种不同去雾算法在Forest和Train两幅图像中的定性结果。这些定性结果验证了本文算法的恢复图像明显优于其他四种现有算法。使用GPR[2]和PDE算法[9]获得的结果在局部区域存在低对比度的现象，使用KRM算法[15]获得的结果沿边缘具有白度，而使用本文算法获得的结果对比度较高，边缘平滑性更好。因此，综合来说，本文算法成为图像恢复的更优选择。

(a) 有雾图像 (b) PDE[9] (c) KRM[14]

(a) 有雾图像 (b) PDE[9] (c) KRM[15]

3.2 客观分析

为了验证本文去雾算法的性能，采用对比度增益(CG)，色度指数(CI)和对比噪声比(CNR)三个客观指标对测试结果进行评价。

对比度增益CG是定义有雾图像和恢复图像的平均对比度之间的差异，该值越高，表示恢复图像的对比度质量越好：

(25)

色度指数CI估计恢复图像中的颜色质量。通常，有图图像可能具有更多的白度，导致图像的CI值较小，RGB空间图像的CI值的计算公式为：

(26)

式中：σ、μ分别表示图像的标准差和平均值；I1=IR-IG，I2=0.5×(IR+IG-IB)，IR、IG和IB分别表示图像I在亮度、色调和饱和度空间上的值。

对比噪声比CNR是指两个相邻区域之间信号强度差异与图像噪声的比率，常用来评估细节检出的可能性，信号强度差异越大，图像噪声越小，CNR则越大：

(27)

式中：SA、SB分别表示区域A和B的信号强度；σN是图像噪声的标准差。

将本文算法与四种不同算法的性能进行比较，图4-图6分别给出了不同算法在CG、CI、CNR方面的测试结果。可以明显看出，本文方法在CG、CI、CNR三个指标上比其他去雾方法表现更好，明显地体现出本文方法在去雾方面的优越性。

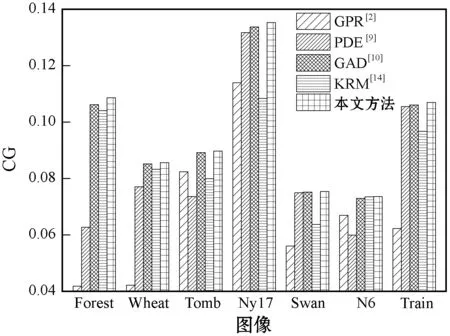
图4 不同算法在CG方面的性能表现

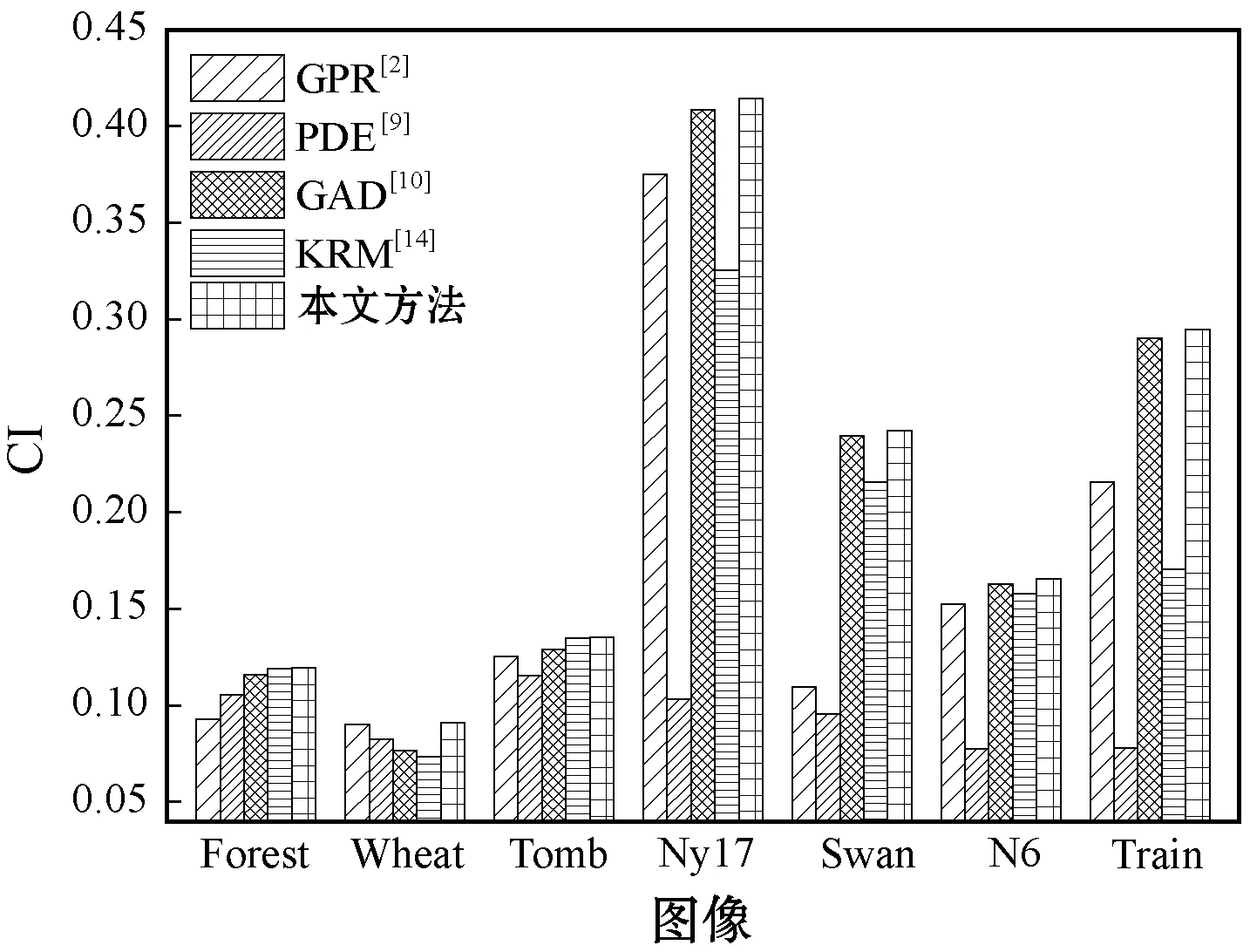
图5 不同算法在CI方面的性能表现

图6 不同算法在CNR方面的性能表现

将本文算法与基于傅里叶域[10]的分数阶各向异性扩散算法所花费的计算时间进行比较。从表1中可以看出，本文算法所花费的时间不到傅里叶域算法所用时间的一半，计算效率大大提高。

表1 基于空间域和傅里叶域算法的计算时间

4 结 语

现有各向异性扩散方程可以有效地恢复模糊图像，但是在去雾过程中容易出现模糊边缘细节的现象。针对这一问题，本文提出一种基于分数阶非线性各向异性扩散的去雾算法，通过对扩散过程进行多次迭代来精细估计大气光传输图。实验结果表明，本文算法在多个指标方面优于其他算法，而且在有效突出去雾图像细节的同时，计算效率也得到提升。