基于深度小波去噪自动编码器的轴承智能故障诊断方法

李晓花 江星星

1(商丘职业技术学院 河南 商丘 476000)2(苏州大学城市轨道交通学院 江苏 苏州 215137)

0 引 言

随着科学技术的迅速发展，现代旋转机械呈现出高速、大规模化、集成化的特点，并在不同行业中起着越来越重要的作用[1]。滚动轴承不仅是旋转机械中最重要的部件，也是一种易受损部件，因此，能够自动、及时地识别轴承运行状态对于减少意外停机和经济损失变得越来越重要[2]。

智能诊断是近年来机械故障检测技术的新的发展趋势，它能够有效地分析收集到海量数据，并自动提供可靠的诊断结果[3-4]。在各种智能诊断方法中，人工神经网络(Artificial Neural Network,ANN)和支持向量机(Support Vector Machine,SVM)是近几十年来应用最广泛的两种方法[5-6]，但它们的诊断性能在很大程度上依赖于特征提取和选择，如何针对不同的诊断任务从原始特征集中选择最敏感的特征向量是限制上述方法的关键问题。因此，亟需发展一种深度架构，能够实现对原始振动数据的无监督特征学习。

DAE是一种无监督的特征学习模型，由于其兼容性较强得到了广泛的关注。然而，将标准DAE直接应用于轴承智能故障诊断还是存在着一定的难度。因为在实际工程中，从轴承收集到的振动信号往往十分复杂，噪声较大且不稳定，而标准DAE的激活函数Sigmoid函数很难建立轴承各种状态与振动信号之间的映射关系[7]。小波函数能够通过改变尺度因子和位移因子，具有良好的时频局部化特性和聚焦特征，并且成功地作为新激活函数构建了所谓小波神经网络[8]。本文提出一种基于深度小波去噪自动编码器和极限学习机的新型方法，用于滚动承轴的智能故障诊断。实验结果表明，该方法克服了对手动特征提取的依赖性问题，且比传统方法和标准深度学习方法更为有效。

1 深度小波去噪自动编码器

1.1 标准去噪自动编码器

去噪自动编码器作为一种无监督神经网络[9]，能够使得输入数据和输出结果之间的重构误差最小化。标准去噪自动编码器的结构如图1所示，包括输入层、隐含层和输出层。

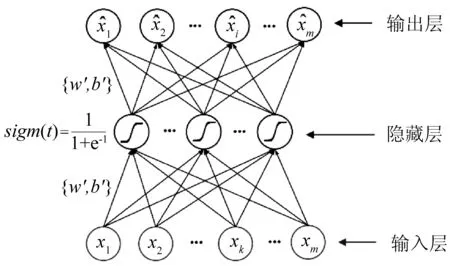
图1 标准去噪自动编码器结构图

该编码器的激活函数为Sigmoid函数。对于训练样本x=[x1,x2,…,xm]T，首先通过Sigmoid激活函数将输入数据转换为一个隐含特征向量h=[h1,h2,…,hp]T，相应的转换公式如下：

h=sigm(Wx+b)

(1)

sigm(t)=1/(1+e-t)

(2)

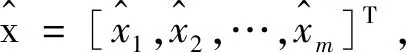
(3)

式中：θ′={W′,b′}为隐含层与输出层之间的参数集。训练去噪自动编码器是为了将参数集θ={θ,θ′}={W,b,W′,b′}的重构误差优化至最小。对于含有S个未标记训练样本的样本集{x1,x2,…,xS}，定义重构误差为：

(4)

1.2 构造深度小波去噪自动编码器

标准去噪自动编码器具有强自适应、强鲁棒性、强推理能力和无监督特征学习能力的特点[10]。小波变换具有时频局部化和聚焦特征。因此，结合标准去噪自动编码器和小波变换的优点来解决实际问题具有重要的意义。本文提出一种新型的无监督神经网络——小波去噪自动编码器，它具有较强的信号捕获能力，能够从复杂和非平稳振动信号中获取典型信息。

WAE模型用小波函数作为激活函数，从而代替传统的Sigmoid函数，可以用不同的分辨率描述不同的信号特征。输入层和输出层都有m个节点，隐含层有p个节点。对于一个训练样本x=[x1,x2,…,xm]T，隐含层节点j的输出为：

(5)

式中：ψ(·)为小波激活函数;xk为训练样本的第k维输入;Wjk为输入节点k与隐含层节点j之间的连接权值;aj和cj分别表示隐含层节点j的小波激活函数的尺度因子和平移因子。

Morlet小波在时域被定义为复指数函数，在频域具有高斯窗的形状。在各种小波函数中，由于Morlet小波与机械脉冲信号有着很高的相似性，是应用最广泛的旋转机械特征提取和故障诊断方法[11]。但是，Morlet小波在不同中心频率条件下可能表现出不同的性质，当中心频率值大于5 Hz时，Morlet小波作用有限。因此，如何确定Morlet小波的参数对于信号处理是非常重要的。根据参考文献[11]以及从不同工作状况采集的振动信号的要求，本文采用Morlet小波实部作为非线性激活函数来设计WAE，其表达式如下：

ψ(t)=cos(5t)exp(-t2/2)

(6)

基于Morlet小波的隐含层节点j的输出可表示为：

(7)

相应的WAE输出可以表示为：

(8)

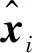
为了更好地获得输入数据的特征并且克服特征学习的过度完备性，通常将基于Kullback-Leibler (KL)散度的稀疏表示技术引入到不同类型的去噪自动编码器的重构误差函数中[12]。定义WAE的改进重构误差函数为：

(9)

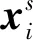
WAE训练的目的是优化参数集θWAE={Wij,Wjk,aj,cj}，使重构误差最小。反向传播算法是一种常用的神经网络训练方法，为了进一步提高收敛速度，引入了动量项。最后，参数的新规则可以表示为：

(10)

(11)

(12)

(13)

式中：η为学习速率;α∈[0.9,1]为动量因子;E(t)为第t次迭代时WAE的重构误差。

为了进一步提高学习特征的质量，在WAEs的基础上构建深度架构。由三种WAE组成的DWAE逐层构建：首先，利用采集到的振动数据训练第一个WAE,将采集到的振动数据从输入层转换为隐含层，学习特征Ⅰ;然后，特征Ⅰ成为第二个WAE的输入，用来获取特征Ⅱ;第三个WAE将继续按照该模式进行训练，以获得特性Ⅲ。最后，将学习到的最高层次特征输入分类器进行故障模式识别。

2 智能故障诊断

2.1 极限学习机

为了实现故障模式的自动识别，需要在DWAE的顶层增加一个智能分类器。极限学习机(ELM)是一种新型的分类器[13]，它可以看作是一种单隐含层前馈神经网络。与其他分类算法不同，ELM在训练精度和训练速度方面表现出不错的特点，比较适用于监督学习和非监督学习问题[14]。

(14)

式中：g(·)为ELM的Sigmoid激活函数;Wj=[wi1,wi2,…,wip]T为隐含层节点i的输入权重;βi为隐含层节点i的输出权重;bi为隐含层节点i的偏差;oj为第j个样本的ELM分类器的结果输出。式(14)可以简写成：

Hβ=T

(15)

(16)

(17)

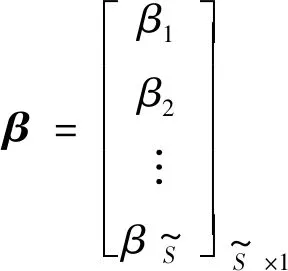
式中：H为隐含层的输出矩阵，H的第i列是对应训练样本的第i个隐含层节点输出;β是隐含层和输出层之间的输出权重向量;T是目标矩阵。ELM训练旨在找到参数β在输出矩阵和目标矩阵之间的最小误差。根据参考文献[15]，输出权重β为：

β=H+T

(18)

式中：H+为隐含层输出矩阵H的Moore-Penrose广义逆。

2.2 智能故障诊断流程

该方法的流程如图2所示，一般步骤如下：

图2 智能故障诊断流程

1) 利用加速传感器测量滚动轴承的振动数据。

2) 不进行任何信号预处理或特征提取，将原始振动数据分为训练样本和测试样本。

3) 构造深度小波自动编码，用于原始振动数据的无监督特征学习。

(1) 选择Morlet小波作为激活函数，用来设计小波去噪自动编码器。

(2) 使用训练样本对第一个WAE进行训练，然后使用式(7)和式(8)计算隐含层和输出层的输出。

(3) 使用式(9)计算第一次WAE的损失函数，使用式(10)-式(13)校正参数。

(4) 完成第一次WAE的训练。

(5) 使用第一个WAE的隐含观测量作为第二个WAE的输入数据，可以根据相同的规则进行训练。

(6) 重复步骤(1)到步骤(5)直到最后一个WAE，然后就能成功构造出DWAE，可以对原始振动数据进行无监督特征学习。

4) 利用学习到的训练样本的深度特征训练ELM分类器。

5) 通过测试样本验证该方法的有效性。

3 实 验

3.1 滚动轴承实验数据

以凯斯西储大学实验室的滚动轴承实验数据为研究对象[16]。实验装置如图3所示，主要由三相感应电机、测试轴承和负载电机组成。每个轴承分别在四种不同负荷(0、1、2、3马力)下进行测试，将故障直径分别为0.178、0.355、0.533、0.710 mm的单点故障引入轴承。在驱动端附近放置一个加速度计来收集振动信号。

图3 滚动轴承实验装置

本文利用采集到的1 797 r/min以下的振动数据来构建数据样本。建立了12种轴承运行状态，包括不同的故障类型、不同的故障程度和不同的故障定位。每个轴承状况由150个样本组成，每个样本代表一个采集到的振动信号，包含800个数据点。为了避免诊断结果的偶然性，每种状况随机抽取100个样本进行训练，其余50个样本进行测试。图4为12种承轴状态的原始数据样本(前800个数据点)。

图4 12种滚动轴承运行状况的振动信号

3.2 深度特征评价

每次去噪自动编码器训练或WAE训练的目的都是优化参数，使重构误差最小。将本文方法中最高阶基模型的重构误差曲线与标准DAE的进行比较，如图5所示。可以看出，该方法的重构误差曲线收敛速度更快。

图5 重构误差对比曲线

为了显示该方法的特征学习能力，对DWAE学习的深度特征、DAE学习的深度特征和手动提取的特征质量进行了比较和评价。以第一次实验为例，考虑到DWAE学习的深度特征(80维)、DAE学习的深度特征(100维)和手动提取的特征(80维)均为高维数据，利用核主成分分析(KPCA)进行可视化。图6和图7分别是不同类型特征的二维和三维可视化，其中KPCA1、KPCA2和KPCA3分别代表前三种主要成分。可以看出，与其他两种特征相比，DWAE学习到的深度特征能够更清晰地表示输入数据。主要原因：(1) 所提出的深度模型具有较强的从输入数据中学习代表性信息的能力；(2) 小波激活函数具有时频局部化特性和聚焦特性，对非平稳信号处理非常有效。

图6 KPCA实现不同特征的二维可视化

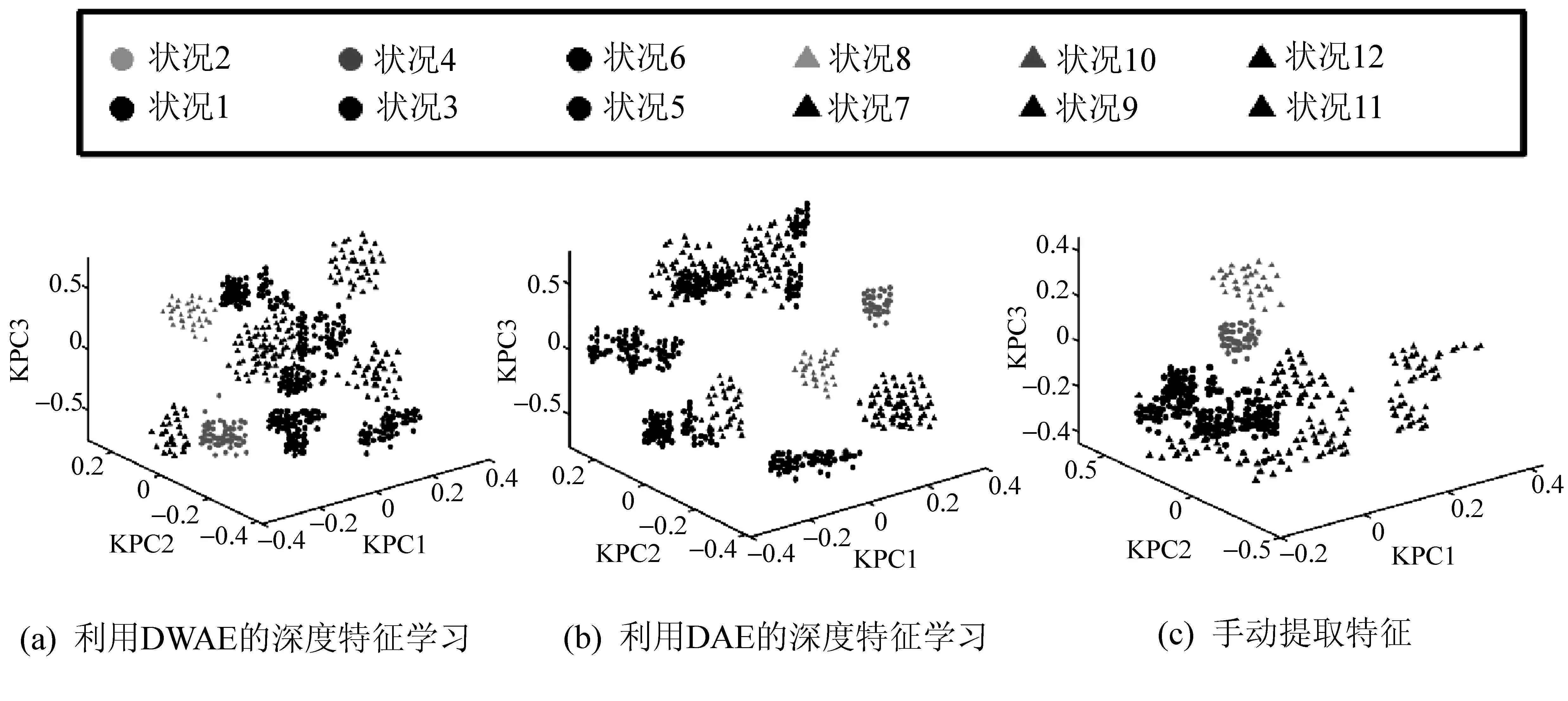
图7 KPCA实现不同特征的三维可视化

为了进一步评价故障模式分类中不同冗余特征的质量，计算了类间协方差SB和类内协方差SW。定义两个参数[17]为:

(19)

(20)

(21)

(22)

类间协方差可以用来描述不同类间的离散程度，类内协方差表示同一类内的聚类程度。一般来说，越大的类间协方差以及越小类内协方差，表明输入数据集具有较强的类区分度。本文采用四个评价指标对不同特征的质量进行综合定量描述：

(23)

(24)

(25)

(26)

式中：tr(A)表示矩阵A的迹。

指标Ji(i=1,2,3,4)结合了类间协方差和类内协方差，计算结果如图8和表1所示。根据评价标准，更大的Ji(i=1,2,3,4)意味着更好的分类结果。可以发现，基于DWAE的深度特征学习的四个评价指标分别是1.277 5、0.391 7、0.625 5和2.669 2，都略大于基于DAE的深度特征学习，且远大于人为提取特征。实际上，利用DWAE的深度特征学习存在着最大的类间协方差以及最小的类内协方差。

图8 不同特征的归一化评价指标

表1 不同特征的定量评价

3.3 对比分析

为了验证本文提出方法的有效性，将该方法与标准DAE、小波神经网络(Wavelet Neural Network,WNN)、BP神经网络(Back Propagation Neural Network,BPNN)、SVM等四种传统的智能诊断方法对同一数据集进行对比分析。其中所有深度学习方法的输入都是800维原始振动数据。标准DAE的分类器有两种类型：传统的Softmax分类器和提出的ELM分类器。本文提出的方法侧重于滚动轴承的智能故障诊断，不需要任何信号预处理或特征提取，这与传统的智能方法完全不同。

另外，WNN、BPNN和SVM有两种输入类型。一个是800维原始振动数据，另一个是从每个频段信号中提取80个特征参数。

其他7种方法的主要参数描述如下：

方法2(标准DAE+Softmax)：采用Softmax分类器。由实验确定，标准DAE的体系结构是800-400-200-100。其学习速率为0.1，迭代次数为120。

方法3(标准DAE+ELM)：通过实验确定，DAE体系结构为800-400-200-100。其学习速率为0.1，迭代次数为120。采用ELM分类器(100-270-12)。

方法4(使用原始数据的BPNN)：由指导原则和经验决定，体系结构为800-1400-12。其学习速率为0.1，迭代次数为600。

方法5(利用手动特征的BPNN)：体系结构为80-150-12，学习速率为0.1，迭代次数为400。

方法6(使用原始数据的WNN)：选择Morlet小波函数作为激活函数。由指导原则和经验决定，体系结构为800-1200-12。其学习速率为0.1，迭代次数为600。

方法7(利用手动特征的WNN)：采用小波函数作为激活函数，体系结构为80-140-12。其学习速率为0.1，迭代次数为400。

方法8(使用原始数据的SVM)：利用径向基函数核。将惩罚因子和核函数半径分别设置为40和0.18。每一个都是通过10倍交叉验证确定的。

方法9(利用手动特征的SVM)：利用径向基函数核。将惩罚因子和核函数半径分别设置为30和0.32。

通过五次实验来验证方法的稳定性，图9为每次实验的详细结果，平均测试精度如表2所示。可以看出，所提出的基于深度小波去噪自动编码器和极限学习机相结合的方法每次实验的检测精度分别为95.5%、95.12%、95.33%、95.05%和95.17%。从表2可以观察到，该方法的平均精度为95.23%，而使用原始振动数据的标准DAE+Softmax、标准DAE+ELM、BPNN、WNN和SVM平均测试精度分别为89.55%、89.83%、49.39%、52.48%和54.07%。在特征提取后，虽然BPNN、WNN和SVM的准确率分别提高到85.14%、88.59%和87.91%，但它们的性能仍然无法与本文方法相比。此外， 本文方法的标准差为0.217 3，远小于其他8种方法。图10给出了所有方法的平均计算时间，包括特征学习阶段和故障分类阶段。本文方法的平均计算时间为255.89 s，而其他方法的平均计算时间分别为266.89、227.6、256.92、31.21、208.71、24.8、163.91和20.41 s。通过比较可知：(1) 小波神经网络、SVM和BPNN的诊断性能在很大程度上依赖于人工特征提取。通过设计一些新特征或从原始的特征集中选择最敏感特征，进一步提高测试的准确性，但是会大幅增加计算时间和难度。(2) 在使用原始振动数据时，深度学习方法(DWAE和DAE)与BPNN、WNN和SVM相比，具有更高的测试精度和更好的稳定性。深度学习方法的优势主要来自逐层特征学习过程，能够从原始数据中自动获取有用的代表性信息。(3) 本文方法的诊断精度略高于采用Softmax或ELM分类器的标准DAE。其原因是该方法充分利用了DAE和小波激活函数，可以进一步提高非平稳振动信号的特征学习能力。(4) 由于隐含层的增加，使得当前深度学习的计算时间大于BPNN、WNN和SVM。然而，随着现代硬件技术和训练算法的快速发展，可以充分相信，各种深度学习模型可以更高效地完成[3]。

表2 不同方法的诊断结果

图9 不同方法的诊断结果对比

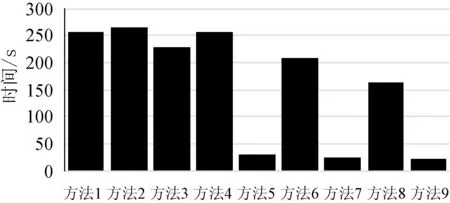
图10 不同方法的平均计算时间

本文提出的DWAE包含一个输入层和三个隐含层，由三个WAE组成。ELM是在DWAE学习到的深度特征数据基础上进行故障分类的，它包含一个输入层、一个隐含层和一个输出层。深度学习模型的框架设计仍然是一个很大的挑战，目前还没有理论方法来解决这个问题。本文采用类似于文献[14]的简单思想，通过实验选择了一种具有三个隐含层的DWAE。式(9)中的稀疏惩罚因子β和稀疏参数ρ是DWAE的两个重要参数。本文采用交叉验证方法来确定最优参数集(β,ρ)，β的候选集为[1,2,3,4,5,6,7,8,9]，ρ的候选集为[0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]。图11为第一次实验的精度与参数集(β,ρ)之间的关系。可以看到，精度对稀疏参数ρ较为敏感，较小的稀疏值似乎是更好的选择。

4 结 语

本文提出一种新型的基于深度小波自动编码和极限学习机相结合的方法用于轴承智能故障诊断。应用该方法对实验得到的轴承振动信号进行了分析，结果表明：

(1) DWAE克服了手动特征提取的依赖，大大地简化特征选取的步骤，而且对比DAE能够更加精确地选择原始振动信号中的敏感特征信号。

(2) 深度学习方法相较于浅层学习来说具有更高的测试精度和更好的稳定性。

(3) DWAE与ELM相结合的轴承智能故障诊断方法能够保证较高的故障诊断率。