基于SC 特征的叶片图像识别研究*

周小亮 丁静军 吴东洋 窦立君 吴东华

（1.南京林业大学信息科学技术学院 南京 210037）（2.南京林业大学信息中心 南京 210037）（3.南京航空航天大学继续教育学院 南京 210016）

1 引言

植物分类学中，常用的方法是根据外部器官的形态，即根据正确描述植物根、茎、叶、花、果等器官形态，通过形态学特征正确识别植物。叶片作为植物光合作用的主要器官，具有叶形、叶缘、叶裂、叶尖、颜色等较强的形态学特征。基于叶片图像的特征提取可实现植物自动分类识别［1～3］，在植物分类、植物病害自动诊断等方面有着重要的研究意义。近年来，国内外学者提出了大量的基于图像分析的叶片自动识别方法。

Osikar［4］等提取叶片的几何特征和矩特征，利用前馈神经网络对15 种瑞典植物进行分类。该方法在样本较少的情况下有较高的识别率，但在形状类似的情况下，识别率明显下降。Cope［5］等提取叶片Gabor纹理特征对32种植物进行识别，但是由于纹理特征过于单一，识别率并不理想。

针对图像特征的叶片自动分类识别技术，国内学者也做了大量研究。王晓峰［6］提取叶片的形状特征和图像不变矩，采用了移动中心超球分类器实现了20 多种植物的识别，平均识别率达到92%。祁享年［7］等通过提取叶片的大小、形状和叶缘参数，证明了形状处理识别植物的可行性。近年来，也有研究者将叶片的纹理特征和形状特征相结以提高识别率。张宁［8］等将叶片几何特征、灰度共生矩阵、纹理特征、分形维数等多特征结合，在100 种植物叶片数据库中进行测试，CSA+KNN 法识别率为91.37%。徐浩然［9］等提出不变量多尺度形状描述方法，该方法具有着较强的缩放、平移和旋转不变性，且对类内差异和铰接形变以及噪声都有着较好的鲁棒性。为了提高匹配的准确性，在做形状特征描述时，所提取的特征针对同一物体的不同形状变化不大，而对不同物体的形状变化较大［10］。

本文基于形状上下文（SC）描述子，提出改进的形状描述子算法（N-SC），通过提取叶片图像的轮廓信息对不同形状叶片能够准确识别，相比传统的SC描述子具有较高的匹配速度及旋转不变性。

2 形状特征提取

形状上下文（SC）算法是 Belongie［11］等于 2002年提出，该算法通过选取有限的点集来描述样本的边界，是一种基于图像形状轮廓的描述方法。不同边界样本点间的相对位置能够较好的描述该形状，且样本点距离参考点之间的距离决定了该样本点在描述形状中的有效程度。为更好地表达位置信息，可采用极坐标系统计样本点相对于参考点的位置关系。

2.1 轮廓提取采样

在形状描述方法中，将轮廓看作是一组点，并假设轮廓可由一组有限的离散点表示。若给出n个点的集合P=｛p1，…，pn｝，则当n→∞时，则可获得连续图像轮廓，故n 越大，轮廓描述越精确，故使用的描述子通过有限的采样点来建立描述子，如图1所示。

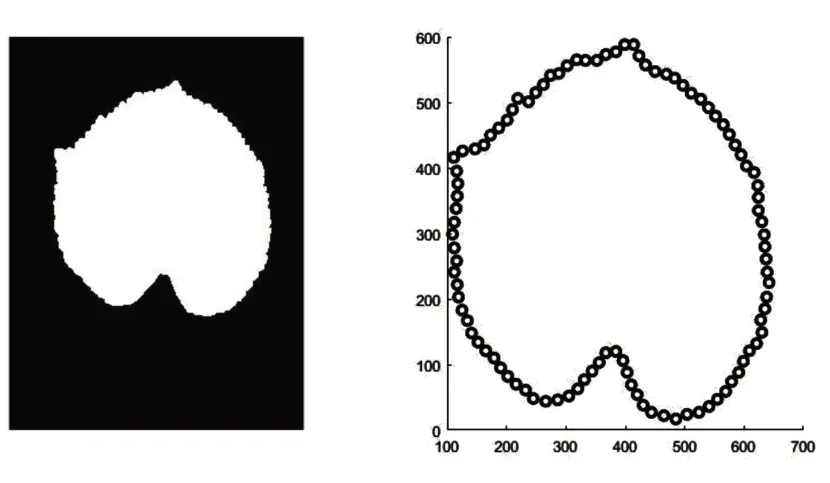
图1 叶片轮廓采样

2.2 形状上下文（SC）

在轮廓矩阵中，若需描述点集P 中的任意一点pi，可通过计算剩余的n-1 个点与该点的位置关系确定。以pi为圆心，r 为半径，将此区域在逆时针方向12 分以形成模板，即以点pi为极点建立极坐标系，这样使得点pi到其他各点的向量简化为极坐标系中每个扇区里的点数分布，如图2所示。

图2 图像轮廓极坐标

由于点阵图像数据基于笛卡尔坐标系，而形状上下文特征提取基于极坐标系，则需坐标系转换。

设极坐标系极轴方向与笛卡尔坐标系水平方向一致，若x0表示所选点为极坐标系原点的横坐标，y0表示所选点为极坐标系原点的纵坐标，x表示边缘点的横坐标，y表示边缘点的纵坐标，则笛卡尔坐标转换极坐标如式（1）与式（2）所示。

其中，r为所选点与极坐标原点距离，θ为所选点与极坐标原点连线与极轴间夹角。

将数据区域用极坐标分割后统计统计其余各点到极坐标原点的角度θ和距离r，建立pi的形状直方图作为pi的描述子，如图3所示。

图3 形状直方图

直方图密集程度代表该区域点的密度，颜色越深，则该区域点的数量越密集。由图（b）和图（c）可知，黑点和红点在数据分布上具有相似性，而蓝点则有较大差异。

2.3 改进的形状上下文描述子（N-SC）

形状上下文（SC）描述子采用直方图描述数据分布，提取轮廓点的个数对计算性能影响较大，即轮廓点个数较多，识别准确度较高，轮廓点较少则结果不精确。若采用χ2 分布来计算匹配代价，即认为当轮廓点数量达到一定程度，则数据分布趋向于正态分布，在获得较高的计算精度的同时，计算时间不会明显增加。

若pi表示第一个轮廓P 中的样本点，qj表示第二个轮廓 Q 中的样本点，g（k）表示 pi 的形状直方图，h（k）表示 qj的形状直方图，则代价值Cij为恒正的值：

由式（3）可知，代价值Cij越小，两个样本点的形状描述子越相似，反之，若代价值Cij越大，则两个样本点相似度越差。

若构建代价矩阵 Mn×n，其中 M 为 Cij的集合，则该代价矩阵M 可描述两个样本点集中每一对样本点间的相似程度。

若H（π）为两个轮廓样本整体的匹配代价，π为一个置换，若 qπ（i）为每个 pi的最优解，可根据代价矩阵M，计算轮廓样本整体的匹配代价。

若希望获得最小的总代价，即求min（H（π））。其中，min（H（π））表示两个轮廓样本总代价最小。

选取Betula pubescens 数据集中的一组叶片图像，如图4 所示，分别采用SC 描述子和SC-X 描述子计算iPAD2_C09_EX01.JPG 与其余三幅图间的匹配代价。

图4 测试叶片

表1 匹配代价

由表1 可知，N-SC 描述子匹配代价远小于传统SC 描述子。其中，图（a）与图（b）匹配代价最小，cost 值为1.3655，说明这两幅图像相似度最高。图（a）与图（d）匹配代价最大，因为图（d）叶片内部具有破损及病害斑块，破损及斑块导致的轮廓数据提取影响了识别效果。

3 基于形状上下文的叶片识别与匹配算法流程

基于形状上下文的图像识别与匹配算法流程如图5所示。

图5 图像识别与匹配算法

由图5可知，叶片识别与匹配算法流程如下。

第一步：利用K-Means算法分割图像；

第二步：利用Otsu算法将图像二值化；

第三步：采样图像边界，每隔四个边界点选取一个轮廓点，得到轮廓点集P；

第四步：坐标转换，将笛卡尔坐标转化为极坐标；

第五步：利用χ2 分布计算匹配代价Cij，得到代价矩阵M；

第六步：利用匈牙利算法评估代价矩阵M，获得最小代价值cost。

4 实验结果与分析

4.1 实验数据

实验采用UCI 数据库中的leaf 数据集。UCI数据库是由加州大学欧文分校为图像识别和机器学习而建立的数据库，该数据库目前共有335 个数据集。UCI-leaf数据集包含40类植物叶片图像，包含木本及草本叶片数据，每类叶片包含数量为8～16张不等的图像，部分叶片图像如图6所示。随机选取其中的5类叶片，每类叶片选取10张图像作为实验数据集。实验平台采用Intel Core i5 处理器，8G 内存，MacOS10.14.2，算法实现采用Matlab 2017b。

图6 leaf数据集部分叶片图像

4.2 实验结果

选取leaf 数据集中Betula pubescens（柔毛桦）、Acer palmaturu（七角枫）、Castanea sativa（欧洲板栗）、Populus alba（银白杨）四种不同的叶片图像。这四张叶片图像在颜色及形状上各有特点。图6中2 及5 分别为七角及五角形状，4 中叶片边界平滑，1 中叶片为椭圆心形，且边缘有轻微破损，5 中叶片左侧中间带有虫洞，2 中叶片背景为灰色。通过N-SC 描述子计算柔毛桦1 与其他三种叶片之间的匹配代价。

图7 叶片图像

表2 图像间匹配代价

根据表2可知，不同形状的叶片，匹配代价cost差异明显。其中图7（a）与图7（c）匹配代价为18.5669，说明这两种叶片相似性最差，图7（a）为阔卵形，而图7（c）叶片为长椭圆形。在三组数据中，图7（a）与图7（d）匹配代价值最小为7.9248，表示两种叶片在形状上最为相似，图7（a）和图（7d）都属于阔卵形，但两者为不同树种，并且图7（d）有虫洞干扰。

为验证N-SC 算法的识别准确性，选取一幅银白杨叶片图像如图8 所示，与数据集中的5 类各10张叶片图像对比，计算匹配代价Cost。

图8 银白杨

选取leaf 数据集中Quercus suber（欧洲栓皮栎）、Populus nigra（黑杨）、Quercus robur（夏栎）、Betula pubescens（柔毛桦）、Populus alba（银白杨）的5 类各10 张图像作为实验数据，结果如表3 所示，其中第5类Populus alba为银白杨。

由表3 可知，银白杨叶片与第5 类即银白杨叶片匹配代价最小，平均Cost 值为5.36327。而该叶片与Quercus robur（夏栎）差异最大，其中银白杨叶片呈卵圆形，掌状5浅裂，而Quercus robur（夏栎）叶片为长倒卵形。银白杨叶片与第二类Populus nigra（黑杨）叶片平均Cost 值为8.00923，说明两者相似度较高，因为Populus nigra（黑杨）叶片与银白杨叶片同都为卵圆形，但黑杨为菱状卵圆形。

表3 匹配代价

统计上述50 幅叶片图像匹配时间，如图9 所示，总匹配花费257.053s，平均单幅图像识别时间5.141s。在总识别时间中，图像分割与轮廓提取算法耗时51.88s，形状上下文描述子建立耗时3.080s，代价矩阵计算耗时0.529s，匈牙利算法耗时200.682s。由此可见，轮廓集匹配阶段耗时最高。

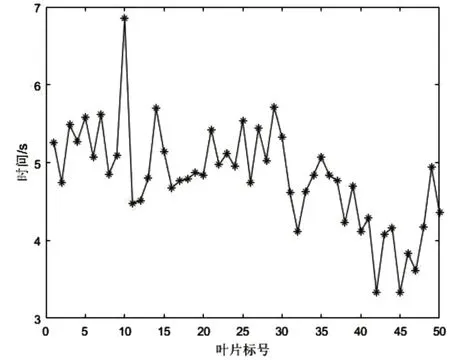
图9 叶片识别时间折线图

由图9 可知，大部分叶片图像匹配时间介于4s～6s 之间，平均的识别时间为 4.8141s。其中，部分叶片图像匹配时间低于4s，只有一幅叶片识别时间高于6s，为6.883s。叶片图像匹配效率与轮廓的复杂程度及采样点数目有关，轮廓越复杂，采样点越多，匹配耗时越长。其中第10 幅图像为欧洲栓皮栎叶片，其形状为长椭圆形，轮廓与银白杨叶片差异较大。而第45 幅为银白杨叶片，其轮廓与待比较叶片相似程度最高。

5 结语

植物叶片形状，即叶片轮廓，基于叶片图像的植物分类方法研究是植物分类学的一个重要研究方向［12］。不同的植物，叶形的变化很大，根据特征数据结合植物分类学知识能够识别叶片的基本形状［13］，以达到快速有效的植物种类识别，对于区分植物、探索植物间亲缘关系具有重要意义。本文提出一种改进的SC 形状上下文描述子（N-SC），在对叶片图像膨胀［14］、腐蚀［15］等预处理的基础上，利用Ostu［16］算子对图像进行二值化处理，进而提取图像的形状特征，使用匈牙利算法计算图像间匹配代价。实验结果表明该算法具有较高的识别准确度。

但该方法也存在一些缺陷，为了保证图像边界的连续性，N-SC描述子选取更多的轮廓点，导致识别时间较长，平均4.8s。该算法可有效区分叶片形状差异较大植物，对于形状相似性较高的叶片图像具有明显的局限性。

在进一步的工作中，可提取关键代表点描述图像轮廓，以减少轮廓点数量，进一步优化匹配代价Min（cost）计算方法。结合叶片纹理信息，可以解决不同植物相同叶片的问题。