计及储能寿命的微电网经济调度

陈名扬， 刘 敏， 余登武，2

（1 贵州大学 电气工程学院， 贵阳 550025； 2 国网重庆电力公司万州供电分公司， 重庆 404100）

0 引 言

随着分布式可再生能源的微电网大量并网，给电网运行带来巨大挑战［1-4］。 微电网是指由可再生能源电源、储能、能量转换装置、负荷监控和保护装置等组成的小型发配电系统。 如何妥善管理分布式能源和储能装置、实现负荷需求响应是实现微电网经济运行最大化的重大课题［5-9］。 微电网经济调度问题是指考虑电网的分时电价基础上，对常规负荷、光伏出力、风机出力进行预测，并充分利用微网中的储能等可调控手段，使微电网运行的经济性最优［10-12］。

目前已有很多学者对微电网调度进行了研究。文献［13-15］对负荷特性进行分类，考虑需求响应，建立微电网经济调度模型，但未考虑风机出力波动性带来的风险。 文献［16］用数学模型描述了不同能源间协调转化的关系，以运行成本为目标，建立了微型能源网日前经济优化调度模型。 文献［17］以用户电能支出成本为目标，考虑天气因素对电动汽车充放电影响，建立了包含电动汽车的家庭微电网经济调度模型。 当前经济调度策略依赖于日前预测的准确性。 文献［18］提出了一种考虑预测误差的微电网能量管理经济调度策略。 文献［19］考虑风电不确定度与阀点效应，建立了以经济成本、环境成本与机组异步度为优化目标的微电网协同优化调度模型。 文献［20］以微电网运行成本和环境保护成本最小化为目标，建立了考虑到电动汽车充放电，以及蓄电池损耗成本和峰谷电价对微电网运行产生的影响的微电网调度模型。 微电网中约束较多，如微网与电网允许交换功率约束、储能的充放电次数以及放电深度等，这些加大了求解难度。

本文在允许微电网与主网进行功率交互的前提下，研究了考虑储能寿命的微电网日前经济调度方法。 首先分析实时电价制定储能购电售电策略，结合功率约束等条件得到了基于规则的贪心［21-22］调度策略。 其次通过自定义粒子种群以及粒子进化方式，得到了基于粒子群算法的调度策略。

1 微电网优化模型

1.1 目标函数

日前经济调度问题是指考虑电网侧的分时电价，在对风机出力、光伏出力、负荷进行日前预测基础上，充分利用微网中的储能等可调控手段，使微电网运行的经济性最优。 所以目标函数应是一天总的运行成本最低，见式（1）：

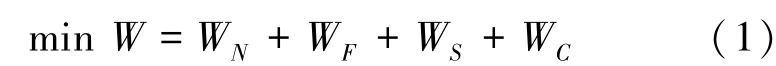
其中，W表示微电网一个调度周期总的运行成本；WN表示微电网一个调度周期内与主网交换费用；WF表示一个调度周期内风机发电费用；WS表示一个调度周期内光伏发电费用；WC表示一个调度周期内储能费用，因为是日前经济调度，一个调度周期指24 h。

研究推得微电网全天与主网交换费用见式（2）：

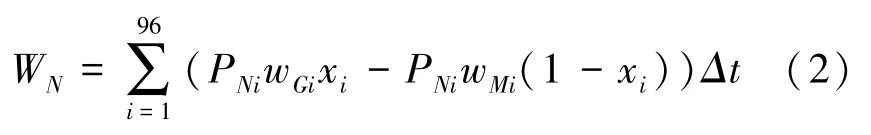
其中，PNi表示第i时段微电网与主网交换功率；wGi表示第i时段购电价格；wMi表示第i时段的售电价格；xi表示第i时段主网功率状态变量：xi ＝0 表示微电网向主网售电，xi＝1 表示微电网向主网购电，一天设为96 个时间段，所以Δt ＝0.25 h。

全天风机发电费用见式（3）：

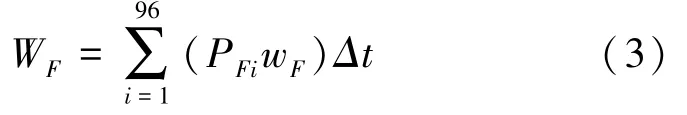
其中，PFi表示第i时段的风机实时功率，wF表示风机发电价格，其值为常数。

全天光伏发电费用见式（4）：

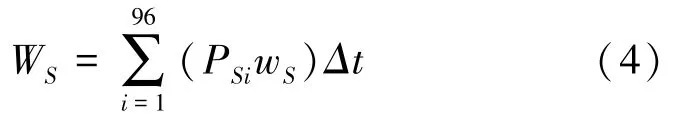
其中，PSi表示第i时段光伏实时功率，wS表示光伏购电价格，其值为常数。

全天储能费用见式（5）：

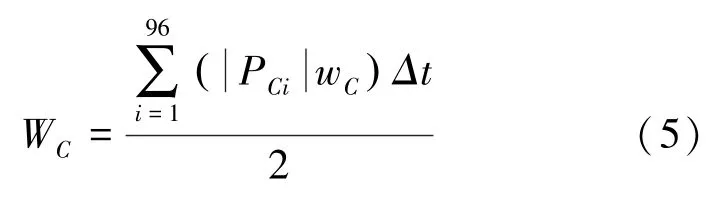
其中，PCi为第i时段储能实时功率，wC为储能从充电至放电状态成本，是一个常数。 储能放电不需要成本，储能充电需要成本。 由于储能需要满足一个调度周期内首末状态的约束，所以储能实时功率应取绝对值，然后价格除以2。

1.2 约束条件

功率平衡约束如式（6）所示：

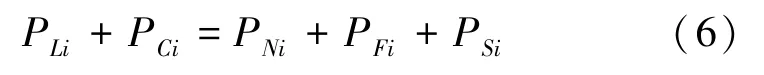
其中，PLi为第i时段的负荷功率。

微电网与主网交换功率约束如式（7）所示：

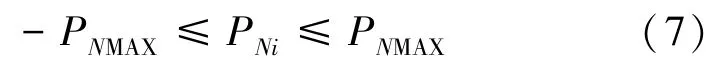
其中，PNMAX表示微电网与主网允许交换的最大功率，是一个常数。

对于储能来说，在一个调度周期内存在充放电次数限制。 如式（8）所示：

其中，N表示一个调度周期储能充放电次数，Nmax表示一个调度周期内（一天）允许的最大充放电次数。

考虑到储能寿命与储能的充放电功率大小有关，单位时间的储能充放电功率有所限制。 如式（9）所示：

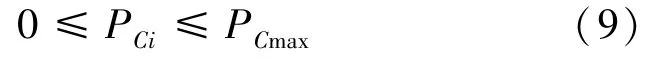
其中，PCmax表示储能允许的最大充放电功率。

为了防止储能过充或过放，储能的荷电状态（State-of-Charge，SOC） 即储能剩余电量与储能容量的比值应满足上、下限值约束。 如式（10）所示：

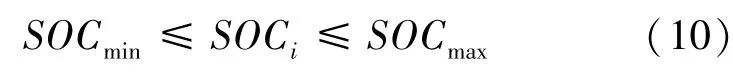
其中，SOCi表示第i时段的储能荷电状态，SOCmax，SOCmin分别表示储能荷电状态的上、下限。

由于风机光伏可以不完全利用，允许弃风、弃光，所以风机和光伏的实时功率应小于或等于预测功率。 如式（11）所示：

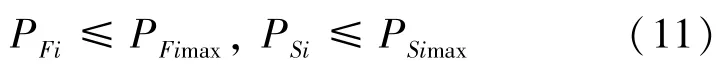
其中，PFimax，PSimax分别为第i时段的风机、光伏预测功率。

2 粒子群算法

粒子群算法常用来求解优化问题，粒子群算法有2 个重要向量，初始化一群粒子，通过适应度函数评价当前粒子的优劣程度。 在迭代寻优过程中，记录每个时刻粒子的个体历史最优解和全局最优解。

速度更新如式（12）所示：

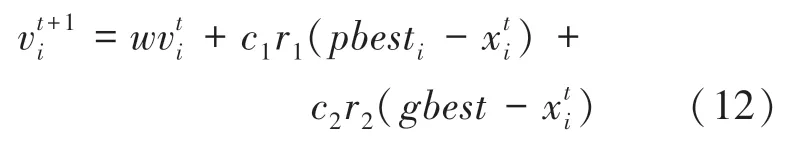
其中，w为惯性权重；c1，c2为学习因子；r1，r2为0 到1 之间的随机数；为第i个粒子当前速度；为第i个粒子当前位置；pbesti为第i个粒子历史最好位置；gbest为粒子种群最好位置。

位置更新如式（13）所示：

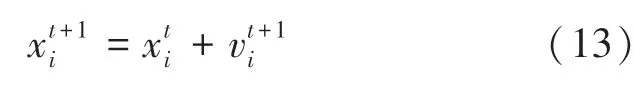
其中，为更新后的速度；为第i个粒子下一时刻位置；为第i个粒子当前时刻位置。

求解带约束的问题，可以通过在粒子速度、位置更新公式上，添加限制实现。 也可以通过罚函数法来求解问题，如果一个粒子不满足条件，就在目标函数上加一个惩罚项，迫使模式在可行域内求解。 假设有一个优化问题如式（14）所示：

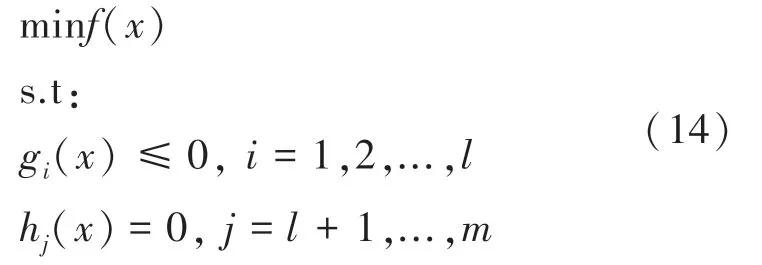
式中有不等式和等式约束。 对约束进行惩罚，得到的适应度函数如式（15）所示：

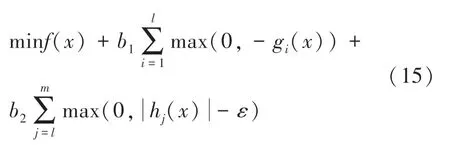
其中，b1，b2为惩罚系数，ε为无限接近于0 的小数，将等式约束转换为不等式约束。 如果一个粒子位置满足等式约束，则等式约束惩罚项值为0，否则为如果一个粒子位置满足不等式约束，则不等式约束的惩罚项值为0，否则为- b1gi（x）。 针对约束，尽量通过对速度、位置更新公式加以限制实现，解决不了的约束，再考虑对目标函数添加惩罚项。

3 算例实现

本文假设该微电网含有风机、光伏、储能（蓄电池）以及常规负荷，微电网系统如图1 所示。

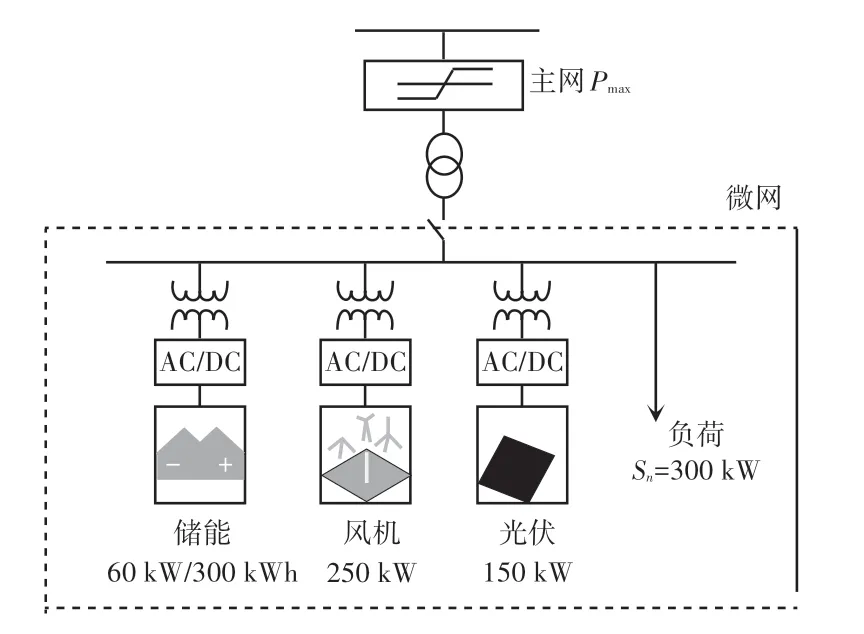
图1 微网系统结构Fig.1 Microgrid system structure

储能额定容量为300 kWh，SOC运行范围为［0.3，0.95］，初始SOC值为0.4，由充电至放电成本为0.2 元／kWh，一个调度周期内储能允许的最大充放电次数为8 次，1 h 充放电功率最大为储能的20%。 风机的装机容量250 kW，发电成本0.52 元／kWh。 光伏的装机容量150 kW，发电成本0.75 元／kWh。 微网与电网允许交换功率不超过150 kW。 一天的售电和购电价格见表1。

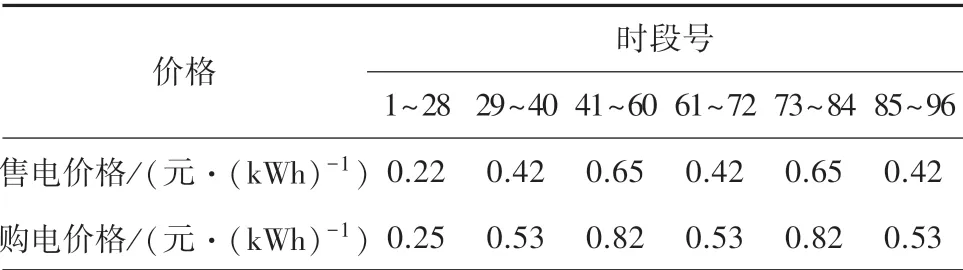
表1 售电和购电价格Tab.1 Electricity sale and purchase prices

风机出力、光伏出力、常规负荷日前预测见图2。

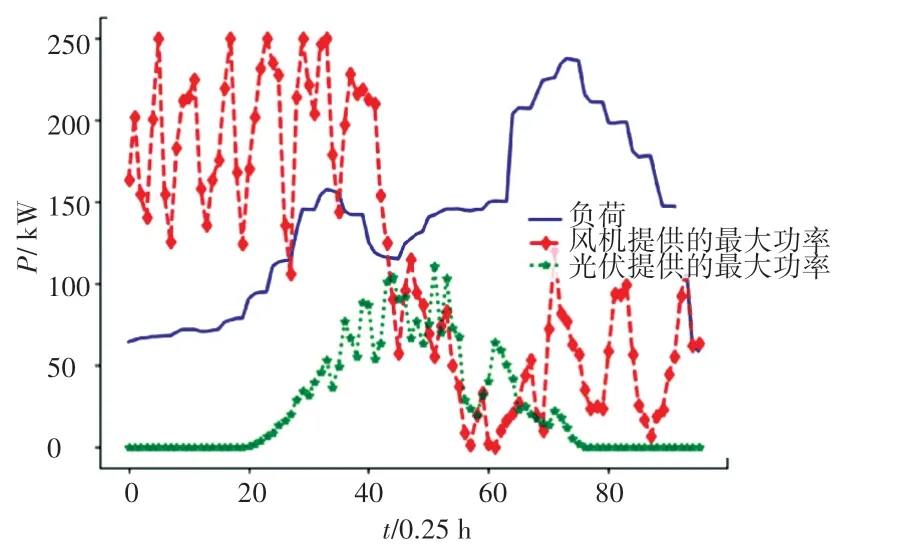
图2 负荷、风机、光伏出力预测图Fig.2 Forecast diagram of load， fan and photovoltaic output

3.1 贪心算法求解

由于有储能约束在，发现问题是全局最优问题，很难直接转化到为求解每一步最优问题。 分析可知，要使每一步都最优，储能得一直放电，显然不可能。

为使负荷供电成本最低，应令储能带来的放电收入与充电成本之差最大，在供电不充足时储能放电收入等于购电价格，充电成本为购电价格+0.2（这时需要从主网购电），储能还可以选择从风机、光伏充电，充电成本等于风机、光伏发电成本+0.2。 于是得到蓄电池各个时段购电售电价格见表2。 从表2中可以知道尽量在充电成本为0.45 元／kWh 时充电，在售电收入为0.82 元／kWh 时放电。

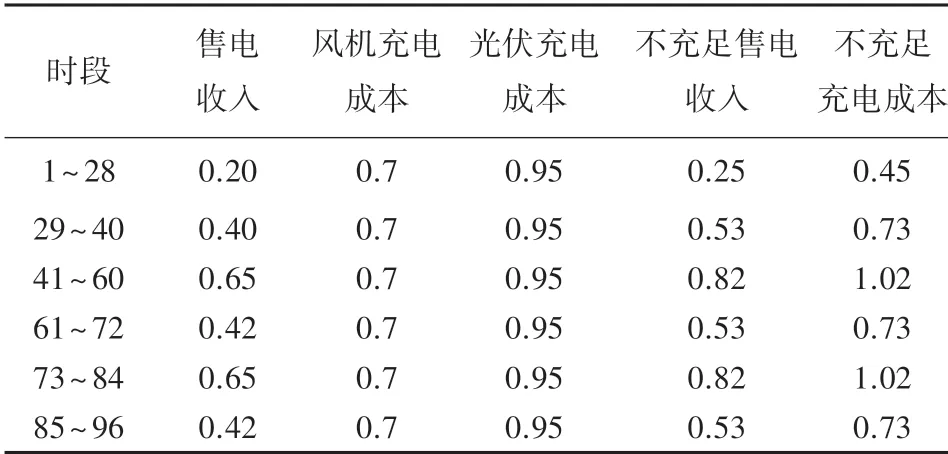
表2 蓄电池售电和购电价格Tab.2 Battery sale and purchase price

分析实时价格，可以知道当电网售价大于可再生能源发电价格时，可再生能源全部不弃；当电网购价小于可再生能源发电价格时，可再生能源全部弃用。 当可再生能源发电价格大于电网售价、小于电网购价时，全部自给（不能多发，全部用于负荷）。

综上所述，可以知道蓄电池售电购电策略见表3。

表3 各时段风机光伏蓄电池状态表Tab.3 Status table of fan photovoltaic battery in each period

根据表3 储能状态，同时结合功率平衡等约束条件，可以编写大量的选e 判断语句确定蓄电池的实时功率。 得到的蓄电池荷电SOC图见图3。

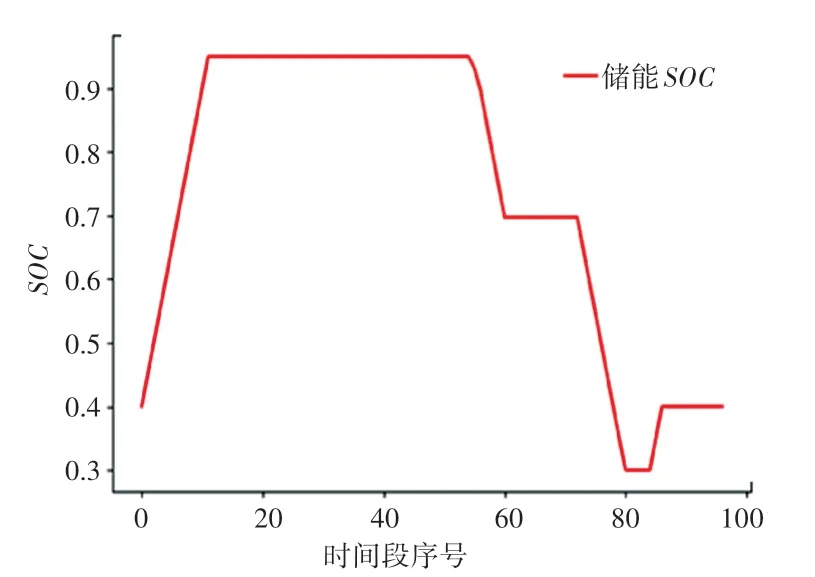
图3 贪心算法求解的储能SOC 图Fig.3 Energy storage SOC diagram solved by greedy algorithm

在确定好储能SOC后，储能实时功率变成已知，原问题变成了线性规划题，可以直接调用线性规划包求解。 求解得到的实时功率见图4。 图4 中，储能功率有正有负，“正”表示储能充电。 求解得到全天总供电费用1 731.79 元。

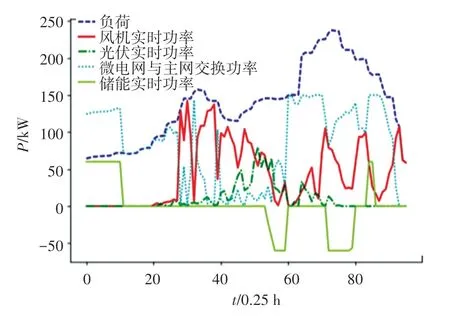
图4 贪心算法求解结果图Fig.4 Solution result graph of greedy algorithm

3.2 粒子群算法求解

虽然粒子群算法原理比较容易理解，但在不同应用里，巧妙地构建种群粒子，以及进化方式，才是关键。 粒子群算法求解示意图见图5。

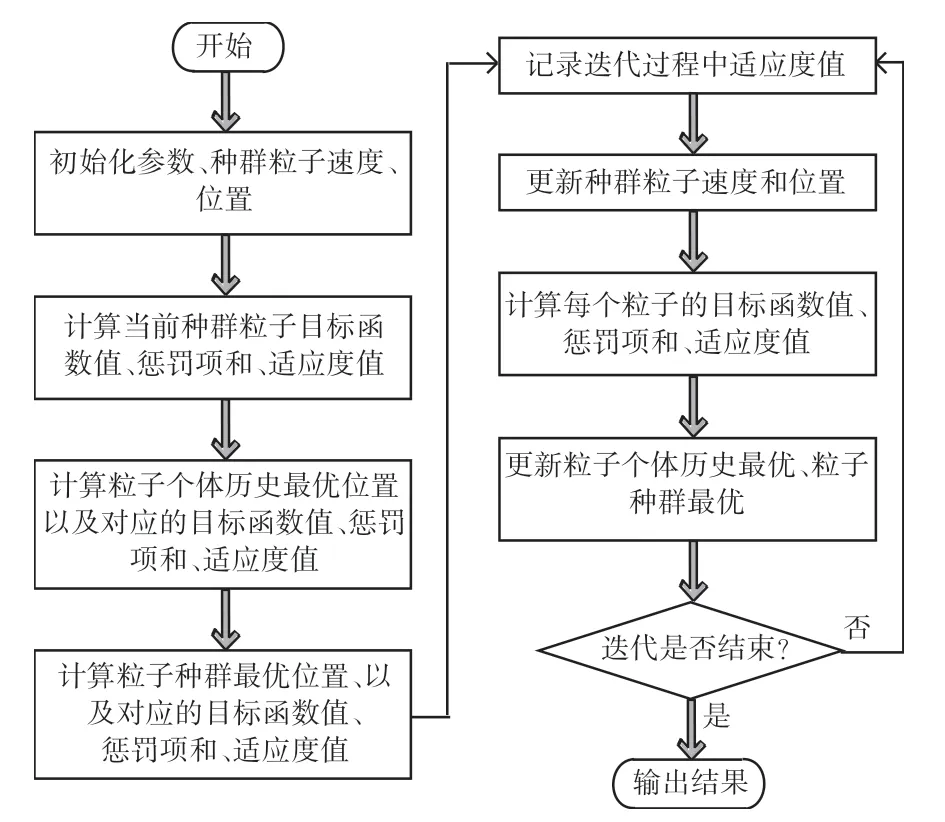
图5 粒子群算法求解示意图Fig.5 Schematic diagram of solving Particle Swarm Optimization algorithm

本文粒子群算法求解步骤如下：

（1）初始化参数，设置种群规模数m ＝200，迭代次数dd ＝50，学习因子c1，c2都为1。 因为储能2次荷电SOC之间存在一次放电，一天有96 个时间段都可以放电，故设置d ＝97，表示一个调度周期内SOC个数。 设置速度的上下限为10 和-10。

（2）初始化种群粒子速度，并使速度处于上下限之间。 初始化种群粒子SOC位置，因为1 h 充放电功率最大为储能的20%，一天有96 个时间段，所以1 个时间段SOC变换最大为0.2*0.25。 根据储能SOC单位时间充放电约束和首末SOC等于0.4的约束，再次添加公式修改种群粒子SOC位置，使之满足约束。 初始化光伏功率和风机功率位置，分别使值在0 到风机、光伏预测功率之间。 根据SOC计算出每个时间段的储能出力。 则微电网与主网交换功率位置可以通过功率平衡计算出，减少粒子数量。

（3）计算当前种群粒子的目标函数值、惩罚项和。惩罚项和等于储能SOC不等于0.4 的惩罚项加上储能一个调度周期内充放电次数大于8 次的惩罚项，再加上微电网与主网交换功率超出上限的惩罚项。 则种群粒子适应度值等于目标函数值加上惩罚项和。

（4）根据步骤（3）得到粒子个体历史最优SOC位置、粒子个体历史最优风机功率位置、粒子个体历史最优光伏功率位置、粒子个体历史最优微电网与主网交换功率位置。 并计算得到粒子群体最优SOC位置、粒子群体最优风机功率位置、粒子群体最优光伏功率位置、粒子群体最优微电网与主网交换功率位置。

（5）更新种群粒子风机功率和光伏功率的速度，并使速度处于速度上下限之间。 根据位置更新公式更新种群粒子风机功率和光伏功率的位置。 并限制位置在0 到风机、光伏预测功率之间。

（6）更新种群粒子SOC的速度，同样使值在速度上下限之间。 根据位置更新公式更新种群粒子SOC位置。 根据储能约束公式修改种群粒子SOC位置。

（7）根据功率平衡约束，更新种群粒子微电网与主网交换功率位置。

（8）计算当代种群粒子的目标函数值、惩罚项和、适应度值。

（9） 将当代粒子位置和粒子个体历史最优位置进行比较，并根据规则进行更新粒子个体历史最优位置。 规则为：如果2 个粒子的惩罚项和都为0，即都是可行域内的解，则比较适应度值，适应度值小的粒子保留。 如果2 个粒子都不是可行域内的解，则惩罚项和小的粒子保留。 如果一个粒子是可行域内的解，另一个不是，则选可行解。

（10）将步骤（9）得到的粒子个体历史最优位置和粒子种群最优位置进行比较，并更新粒子种群最优位置。 规则同步骤（9）。

（11）重复步骤（5）～（10），直至迭代结束。 输出结果。

迭代结果见图6。 求解的SOC曲线图见图7，得到的实时功率见图8，一个调度周期内的总供电费用为1 710.124 元。

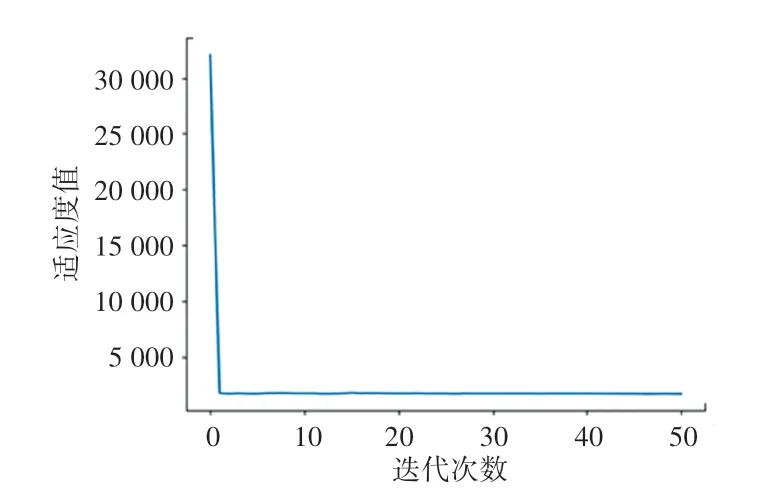
图6 粒子群算法迭代结果图Fig.6 Iteration results of Particle Swarm Optimization algorithm

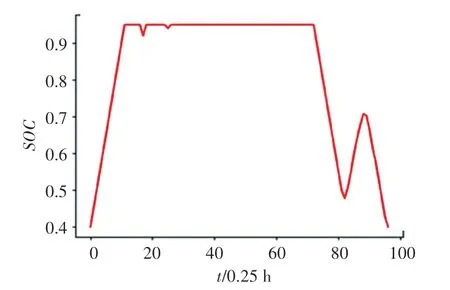
图7 粒子群算法求解的储能荷电状态图Fig.7 State diagram of energy storage charge solved by Particle Swarm Optimization algorithm

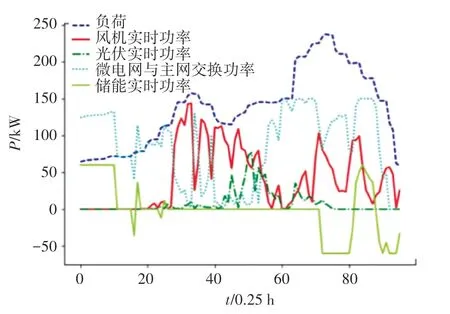
图8 粒子群算法求解结果图Fig.8 Solving results of Particle Swarm Optimization algorithm

3.3 其他情形

本文模型中考虑了储能寿命和可再生能源情况，在现实生活中，微电网可以不使用储能和可再生能源可以部分接纳。 由于这些情况无储能约束，故可以直接用线性规划求解。 和前文结果整合得到表4。从表4 中可以看出，合理使用储能和风光可再生能源，能有效降低供电成本。

表4 各种情形结果表Tab.4 Results for various situations

3.4 结果分析

针对微电网中复杂的储能约束，本文首先分析实时电价，制定规则，基于贪心算法确定了储能的荷电状态，制定规则依赖于专家知识，一旦分时电价发生变化，又需要重新制定规则，并且常常得不到最优解。 接着采用粒子群算法进行求解，有别于常规粒子群只有单一的粒子位置，本文具有种群粒子SOC位置、种群粒子风机功率位置等。 把约束条件通过修改位置更新函数和加惩罚项来实现。 区别于常规粒子群算法中迭代更新选择适应度值小的方法，本文在迭代更新中优先选择在可行域的粒子而不是适应度值小的粒子。

4 结束语

在考虑微电网运行过程中储能寿命（储能充放电次数、深度、单位时间充放电功率）的影响下，本文提出了基于规则的贪心算法调度模型和基于粒子群算法的调度模型。 选取了一个实际微电网进行研究，实验结果表明，本文方法有着很强的可行性，为微电网日前经济调度提供了快速有效的方法。