面向不平地面的双足欠驱动步行稳定控制

姚道金 董文涛 王晓明 杨 林

1. 华东交通大学电气与自动化工程学院，南昌，330013

2. 华中农业大学机电工程系，武汉，430070

0 引言

仿人机器人具有良好的人机交互亲和力、对复杂环境的适应性，一直是机器人领域研究的热点之一[1]。目前针对仿人机器人的研究多集中于结构设计[2]、步态规划[3]及人机交互[4]等方面。许多著名的机器人被推出：Atlas、ASIMO、“汇童”系列、“悟空”系列等[5]，但机器人在步行过程中，始终存在步态不自然、能耗高等问题[6]。为解决上述问题，近年来，一种更加自然、高效的双足步行方式——欠驱动步行逐渐成为研究热点。但步行过程中欠驱动自由度的存在，导致步行控制非常困难，尤其是在不平地面上[7]。

针对不平地面上欠驱动双足步行，PARK等[8]根据不同步行环境分别设计对应控制器，并使用有限状态机进行控制器切换，进而实现机器人在不平地面上稳定步行。YADUKUMAR等[7]通过采集分析人类步态数据，并结合混杂零动态的方法，实现AMBER机器人在不平地面上行走。DAI等[9]将地面作为外部扰动，通过增益L2量化机器人对地面干扰的鲁棒性，通过鲁棒控制实现机器人在不平地面上的行走。NGUYEN等[10]应用两个周期步态构建机器人步态库，结合其良好的形态及结构设计，实现机器人在随机不平地面上的稳定行走。虽然上述算法实现了不平地面上的欠驱动步行，但均基于机器人-地面刚性接触模型，并未考虑地面柔性对步行的影响，与实际情况不符。在真实环境中，地面由许多柔性材质构成，如木板、橡胶等。随着日常环境中柔性材料使用的增加，在欠驱动步行控制中，地面柔性不再是一个可以忽略的因素。

目前，许多研究已经证明地面柔性对欠驱动步行产生影响。PLESTAN等[11]发现机器人RABBIT在柔性地面上步行时，地面柔性导致步行能量消耗增加，影响步行稳定性。AGUILAR等[12]通过流体静力学、动力学分析机器人足部与沙土接触过程中的运动状态变化，并从力学角度探讨柔性地面上的步行控制问题。为解决地面柔性对步行的影响，一些学者基于Dahl模型[13]、LuGre模型[14]和弹塑性模型[15]等建立了机器人-地面接触模型，并通过仿真分析了模型参数对步行性能的影响，但上述建模方法较为复杂，在实际机器人系统中应用十分困难，因此，需建立一种便于实际应用的机器人-地面柔性接触模型。

为实现真实环境中更加高效、稳定的欠驱动双足步行，需同时考虑地形变化和地面材质变化。本文基于人类变速步行特征，提出一种基于质心运动状态的步行稳定控制策略，实现不平地面上的欠驱动双足步行：使用“弹簧-阻尼”系统建立“机器人足部-地面”柔性接触模型；将三维欠驱动步行解耦为前向和侧向的主从控制，通过控制质心位移实现质心速度控制，进而实现机器人稳定步行；最后通过仿真和试验来证明所提控制策略的有效性。

1 不平地面上机器人建模

机器人足部与地面的接触模型是机器人步行系统建模的关键问题之一。考虑地面柔性，本文将柔性地面等效为一系列由黏弹性单元阵列而成的“弹簧-阻尼”系统[16]，如图1所示。每个黏弹性单元中地板均通过x、y、z三个方向上“弹簧-阻尼”构件与地基相连，每个“弹簧-阻尼”构件中弹簧刚度系数为k，阻尼系数为c。双足机器人步行系统是一个强耦合的高度非线性系统，为降低步行系统建模的难度，且便于后续分析与控制，本文忽略三维步行中前向与侧向的耦合，使用解耦建模的方式建立机器人步行系统模型。

图1 双足机器人在不平地面上行走时数学模型

针对步行前向平面(图1a)。机器人包括5个自由度q1、q3、q4、q7、q8，其中，q1为欠驱动自由度；机器人大小腿的长度和质量分别为lt、lc和mt、mc，膝关节质量为mk，髋部质量为mH(2个髋关节和腰部质量总和)。机器人步行过程中，支撑足在x、y和z方向上的位移分别为xst、yst和zst，摆动足在x、y和z方向上的位移分别为xsw、ysw和zsw。定义支撑足末端-地面接触点和髋关节连接线与竖直平面的夹角为θ，机器人步行过程中θ单调增大，可将其作为步行系统的虚拟时间变量。

根据机器人与地面接触情况，一个完整步行周期可分为单足相和双足相两个阶段。在步行单足相阶段，机器人有且仅有一足与地面接触，使用拉格朗日建模法得到机器人单足相动力学方程：

(1)

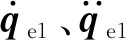
(2)

在机器人步行双足相阶段，支撑足与摆动足均与地面发生接触，使用拉格朗日建模法，得到前向平面机器人双足相动力学方程：

(3)

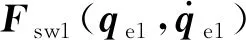
(4)

由式(2)和式(4)得到前向平面一个完整步行周期内机器人动力学模型：

(5)

针对步行侧向平面(图1b)，机器人包括3个自由度q2、q5和q6，髋关节质量为mh，腰部质量和宽度分别为mb和w。与前向平面类似，使用拉格朗日建模法，得到侧向平面机器人单足相动力学方程：

(6)

(7)

机器人步行双足相阶段，使用拉格朗日建模法，得到侧向平面机器人双足相动力学方程：

(8)

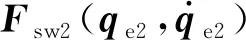
(9)

由式(7)和式(9)得到侧向平面一个完整步行周期内机器人动力学模型:

(10)

2 不平地面上欠驱动步行控制策略

已有研究表明，人类正常步行时质心竖直方向波动为腿长的0.04倍左右，质心在侧向波动为腿长的0.033倍左右，前向运动方向为人类主动运动方向，侧向运动对前向运动影响忽略不计,因此，三维步行控制可转化为前向和侧向的主从控制[17]。根据“机器人不倒”这一双足步行稳定性的最直观表述，笔者已提出一种基于步行速度的欠驱动步行稳定性判定方法：如果机器人步行速度能够收敛于一个已被证明的可维持步行的速度，则机器人处于稳定状态[18]。可将机器人质心速度进行分解，分别控制质心速度在前向和侧向平面内对理想速度的跟踪，进而实现机器人欠驱动稳定步行。

在机器人步行前向平面，“机器人-地面”这一复杂的多输入-多输出系统可简化为基于质心位移和质心速度的单输入-单输出系统。在控制策略中引入自适应质心位移控制系数，根据地形变化调整该控制系数，修正质心位移，实现前向平面质心速度控制。在步行侧向平面，可使用倒立摆模型对步行系统进行简化，通过控制质心侧向位移对前向位移的跟踪，保证侧向平面与前向平面运动相匹配。控制策略结构如图2所示。控制器根据第j-1周期机器人步行状态规划第j周期机器人步态。

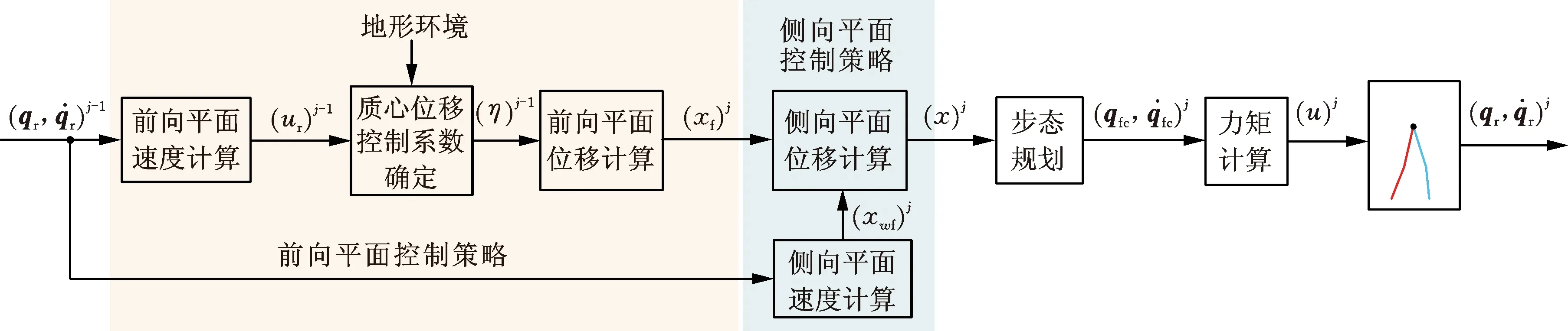
图2 控制策略框图

2.1 前向平面控制算法

观察人类步行姿态发现，通过调整身体姿态可实现步行速度控制：身体前倾，步行速度增加；身体后仰，步行速度降低。人类在不平地面上步行时，将根据地形变化进一步调整身体姿态，实现步行速度控制。因此，笔者提出一种基于质心运动状态的欠驱动步行控制策略，实现机器人在不平地面上稳定步行。选择步行单足相终止时刻质心水平速度uf为控制输出，单足相终止时刻质心与支撑足相对位置的水平分量xf为控制输入，机器人步行系统被简化为一个单输入-单输出系统。控制策略通过调整xf实现uf的控制，进而实现机器人稳定行走。

双足机器人在不平地面上行走时，由于地面不平整，导致其足部落地点不在同一平面上,因此，可根据足部落地点将不平地面等效为不同倾斜角度的斜坡，如图3所示，其中，γi为对应不平地面的等效斜坡倾角。为确定xf与uf的映射关系，将“机器人-地面”模型等效为“杆-地面”模型。根据机器人步行单双足相，等效的“杆-地面”模型可分为碰撞子模型和摆动子模型；为确定两个子模型的切换时间，使用“杆-地面”接触点处水平速度衰减率λ来判断。在t1时刻，当机器人足部-地面接触点处水平速度衰减率为λ时，等效模型由碰撞子模型转换为摆动子模型。

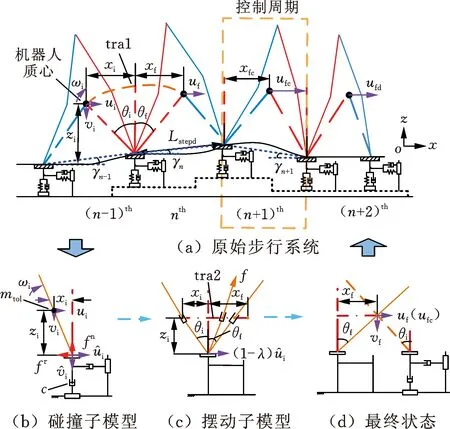
图3 不平地面上等效运动模型

碰撞子模型的求解分为以下两个步骤：

(1)假设杆仅受水平方向地面作用力，然后使用中值定理对杆的状态进行修正。仅受水平方向作用力时，碰撞终止时刻杆质心状态方程为

(11)

(12)

(2)增加竖直方向地面反力修正质心状态，得到碰撞终止时刻杆质心状态方程:

(13)

在摆动子模型中，使用倒立摆来描述杆运动状态。为便于分析，将倒立摆质心运动轨迹简化为一条直线，如图3c所示。得到等效摆动子模型中质心能量变化:

(14)

式中，θi、θf分别为摆动的始末状态角。

综合以上各式，得到一个完整步行周期内等效模型质心能量变化：

E=Kf+ΔW

(15)

Kf=mtol(u2+v2+ρ2ω2)/2

经过一个完整步行周期后，杆质心的水平速度为

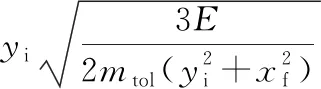
(16)

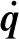
(17)

设机器人步长为Lstepd，使用ufd作为已被证明可维持机器人稳定步行的质心速度[16,18]，则在x=xi处使用一阶线性化，得到下一步行周期质心位移xfc:

xfc=χ(λ,η,vf,uf,xi,yf,Lstepd,ufd)=xf+ηΔxf=

(18)

其中，η为与不平地面等效斜坡倾角γi相关的质心位移调整系数。由图3可知，当γi>0时，地面高度增加；γi<0时，地面高度降低，本文的等效斜坡倾角在[-10°,10°]范围内。当机器人在不平地面上行走时，控制器首先根据测量得到的地形数据计算等效斜坡倾角γi，然后根据γi对参数η进行调整，最后利用式(18)得到调整后的质心位移xfc，实现质心速度uf对理想速度ufd的跟踪，进而实现机器人稳定步行。

由于本文所提控制策略需要根据下一步行周期地形变化计算等效斜坡倾角，故步行环境需要已知。但与其他已知环境的步行控制策略不同，本文控制策略无需已知整个环境的地形变化，仅需已知下一步行周期地形变化即可，适用于实际机器人步行系统。

2.2 侧向平面控制算法

三维行走失稳的主要原因是侧向运动与前向运动不匹配，故可利用“杆-地面”模型等效机器人侧向运动模型，通过控制质心侧向速度对前向速度进行跟踪，保证侧向运动与前向运动相匹配，实现三维欠驱动稳定行走。

当只考虑机器人侧向运动时，步行类似原地踏步，为降低研究难度，规定侧向运动过程中躯干竖直、髋部保持水平，且忽略前向运动导致的腿长变化。机器人侧向运动过程如图4所示，图4a～图4d所示的4种姿态分别记为A、B、C、D，其中A表示机器人由左腿支撑转换为右腿支撑，B表示左腿支撑机器人运动最大姿态，C表示机器人由右腿支撑转换为左腿支撑，D表示右腿支撑机器人运动最大姿态，状态A-B-C为左腿支撑阶段，状态C-D-A为右腿支撑阶段。

图4 机器人侧向平面运动过程

使用三维线性倒立摆模型描述机器人侧向运动，由其动力学方程可知，等效线性倒立摆的轨道能量为

(19)

其中，x为前向平面质心位移，y为侧向平面质心位移；Ex、Ey分别为前向平面与侧向平面轨道能量。则质心在水平面上投影轨迹方程为

(20)

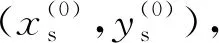
(a) 机器人等效三维线性倒摆模型

由于杆质心前向和侧向位移关系可用双曲线表示，为降低计算量及增加求解速度，本文使用四次多项式对质心轨迹进行拟合，得到质心侧向轨迹方程：

y=a0+a1x+a2x2+a3x3+a4x4

(21)

根据质心在步行初始及终止时刻位移、速度，运动过程中最大摆幅，可确定式(21)中多项式系数a0～a4。

综上，通过控制质心侧向运动对前向运动的跟踪，保证两者相匹配，可实现双足机器人欠驱动稳定行走。

3 试验与分析

3.1 物理样机

为验证所提控制策略的有效性，设计欠驱动双足机器人样机如图6所示，图6中，①为机器人主控器。机器人具有8个主动自由度：左右腿髋关节各2个自由度(图6中②)、膝关节各1 个自由度(图6中③)、踝关节各1个自由度(图6中④)。机器人采用弧状足部设计，忽略足部防滑橡胶皮垫微小变形，步行过程中足部与地面始终保持线接触。步行单足相阶段，足部与地面间无驱动，步行处于欠驱动状态。机器人还配备有移动保护架，当机器人出现不稳定状态时，可对其进行保护。机器人总质量为29.5 kg，高度为743 mm，各部分详细参数见表1。

图6 机器人样机

表1 机器人主要参数

根据表1中机器人参数，在MATLAB中仿真得到一组步长为0.1839m的可维持机器人稳定步行的步态：

qfs=(0.3062,0,0.0661,0.2401,0,0,-0.2382，-0.5459)T

0.7885，3.2917)T

3.2 仿真试验

在进行仿真试验前，需确定不同等效斜坡倾角γi对应的质心位移调整系数η。本文通过仿真试验与差值拟合来确定η的取值，首先选择几个固定倾角作为测试对象，确定可维持机器人稳定行走的η取值范围；然后根据质心速度的最大超调量和调整时间优化η取值；最后使用多项式插值确定不同等效斜坡倾角的η值。

以刚度系数k=24×104N/m、阻尼系数c=32×105N·s/m作为地面柔性参数，将本文研究的等效斜坡范围[-10°,10°]平均分为40份，对机器人步行前100周期进行分析。定义NΔ=5为机器人质心水平速度达到稳态误差5%内所需调整周期数，MP为质心速度的最大超调量，Γi为目标函数，Γi最小值对应η最优值。有

(22)

以等效斜坡倾角为6°时为例，记录机器人在η取不同值时对应质心水平速度的变化情况，如图7所示。由图7可知，η值在(0,0.5]内，机器人质心水平速度可以收敛，η最优值为0.35。

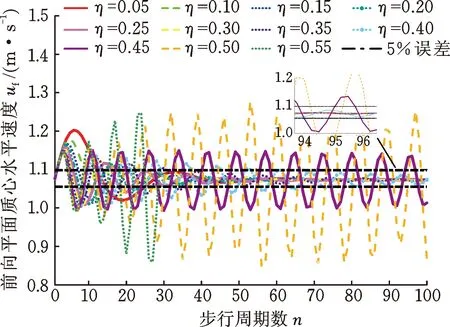
图7 等效斜坡倾角为6°时uf变化情况

同理，得到等效斜坡倾角在[-10°,10°]内机器人可维持步行的η可取值和最优值，如图8所示。其中，蓝色区域为η可取值，红色星号点为测试点处η最优值，粉色曲线为拟合得到的[-10°,10°]范围内η最优值。

图8 η取值范围与最优值

确定不同等效斜坡倾角γi对应的质心位移调整系数η后，进行仿真试验。试验随机生成3组不平地面环境，机器人在每组环境中需完成30周期步行，计算不平地面的等效斜坡倾角，如图9a所示，其中，倾角范围均在[-10°,10°]内。分别使用本文提出控制策略与已有的混合零动态(hybrid zero dynamic, HZD)[19]方法进行仿真试验，验证所提控制策略的有效性。记录3次试验过程中步行单足相终止时刻，2种控制器作用下前向和侧向平面质心水平速度uf和wf的变化趋势，如图9b、图9c所示。由试验结果可知：

(1)在混合零动态方法作用下，机器人无法完成不平地面上步行试验，3次试验分别完成了7、11、10周期步行后，uf和wf发散，机器人失稳。

(2)在本文所提出控制策略的作用下，uf和wf均可稳定在一定范围(uf处于0.4～1.5 m/s区间内，wf处于0.1～0.9 m/s区间内)内，与所提欠驱动步行稳定判据相符，实现了机器人在不平地面上的稳定步行。

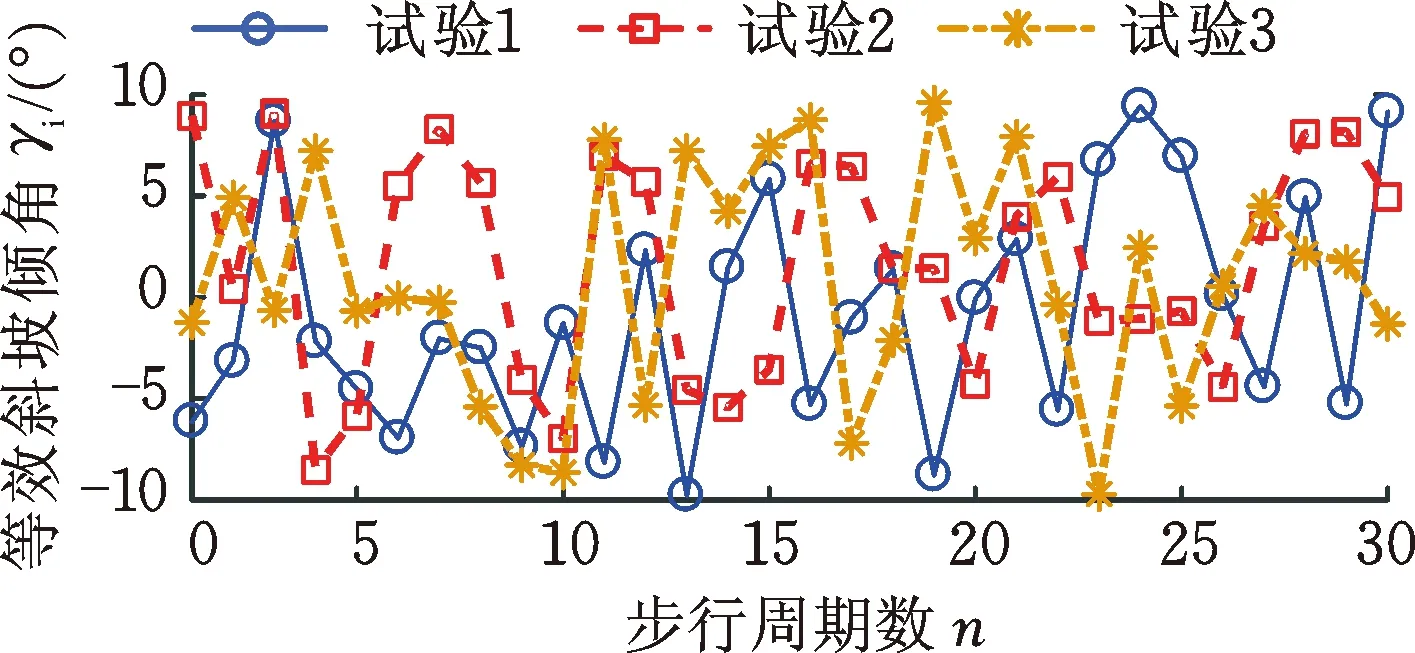
(a) 三组工况下不平地面对应等效斜坡倾角

3.3 样机试验

使用本文所提控制策略与混合零动态方法进行样机试验，记录不平地面上机器人步行过程，如图10所示：首先，机器人在木地板上完成3个周期平地步行后，左腿支撑右腿迈上PVC橡胶地板，如图10a～图10d所示；其次，右腿支撑，左腿迈上PVC橡胶地板，如图10e～图10h所示；然后左腿支撑右腿摆动，平地步行1个周期后，右腿支撑左腿迈下木地板，如图10i～图10l所示；最后，左腿支撑右腿摆动，平地步行1 个周期后，机器人迈下PVC橡胶地板。

(a) DSP

记录2种控制器作用下，3次步行试验过程中单足相终止时刻，前向和侧向平面质心水平速度uf和wf变化趋势，如图11所示。由试验结果可知：

(1)在混合零动态方法作用下，机器人无法实现不平地面上稳定步行，3次试验分别完成了4、5、4周期步行后，机器人失稳。

(2)本文所提控制策略可适应地面材质和地形的变化，实现机器人在不平地面上稳定步行。控制器从第3周期开始工作，uf下降趋势得到抑制，但由于地面高度增加，uf出现衰减，且3次试验uf平均衰减量为0.058 m/s。

(3)机器人迈向木地板时，由于地面高度变化较小(高度差为5 mm)，故质心速度波动不明显；迈向PVC橡胶时(高度差为15 mm)，地面高度变化较大，uf显著提高，3次试验uf平均增量为0.0423 m/s。之后为抑制uf增大，控制器减小质心位移输出，证明所提控制器可抑制地形变化对质心速度产生的影响。

(a) 前向平面质心水平速度uf变化趋势

4 结论

(1)使用“弹簧-阻尼”系统建立“机器人足部-地面”柔性接触模型，采用解耦建模的方式建立了“机器人-地面”耦合动力学模型。

(2)通过观察人类步行特征，提出一种基于质心运动状态的欠驱动步行控制策略，将三维欠驱动步行解耦为前向和侧向的主从控制，通过控制质心速度实现机器人稳定步行。

(3)通过与已有的混合零动态方法进行对比试验，证明了本文所提控制策略的有效性。

本文实现了不平地面上欠驱动步行，但不平地面的起伏较小，如何对控制策略进行改进，使其适用于地面起伏更大的环境，是下一步研究的主要方向。