磁阻式电磁蓄能无针注射系统的设计与实验研究

倪玉吉 王明娣 陈添禹 张 晓 倪 超 刘金聪

苏州大学机电工程学院，苏州，215131

0 引言

为解决有针注射方式引起的针刺疼痛、感染等问题，科学家提出“无针注射”的概念，即通过一定的动力系统将药液以高压、高速、超细方式射出，投送到组织中去[1]。

国外对无针注射系统的研究起步较早， NAKAYAMA等[2]采用运动边界法模拟了气动式无针注射系统安瓿中液体射流通过喷孔的运动，利用LES/VOF技术对流体动力学进行了模拟，SCHRAMM-BAXTER等[3]通过仿人皮肤注射实验，研究了穿刺深度及扩散宽度与实验材料弹性模量之间的关系。国内近期也开展了相应的研究，赵丽娜[4]对高压无针注射系统进行了结构细化和关键参数的理论计算，通过小孔喷射模型和液体撞击模型发现，随着注射动力的增大，注射深度增大。冯利军[5]以音圈电机为动力源，进行电磁力驱动无针注射系统设计，建立了注射过程的数学模型，分析了系统相关参数对射流滞止压力的影响。

现有无针注射系统存在驱动力小、体积大、注射效率低、结构复杂等缺点，笔者在前人研究的基础上，设计的一种磁阻式电磁蓄能无针注射系统包括电磁驱动装置和安瓿两个主体部分、控制电路等次级部分，缩小了无针注射系统的体积，扩大了驱动力的可调范围。

1 电磁驱动模型建立与设计仿真

1.1 驱动原理

如图1所示，磁阻式电磁无针注射系统由电路控制部分和电磁动力部分组成[6]。驱动过程如图2所示，通电线圈产生磁场，铁心被磁化。在磁场力作用下，铁心向磁阻减小的方向移动。铁心运动到线圈中心时，受到的电磁力最小，一般认为此时的铁心不受力[7]。铁心从线圈中心继续往前运动时，运动铁心受到的电磁力将变成阻力。

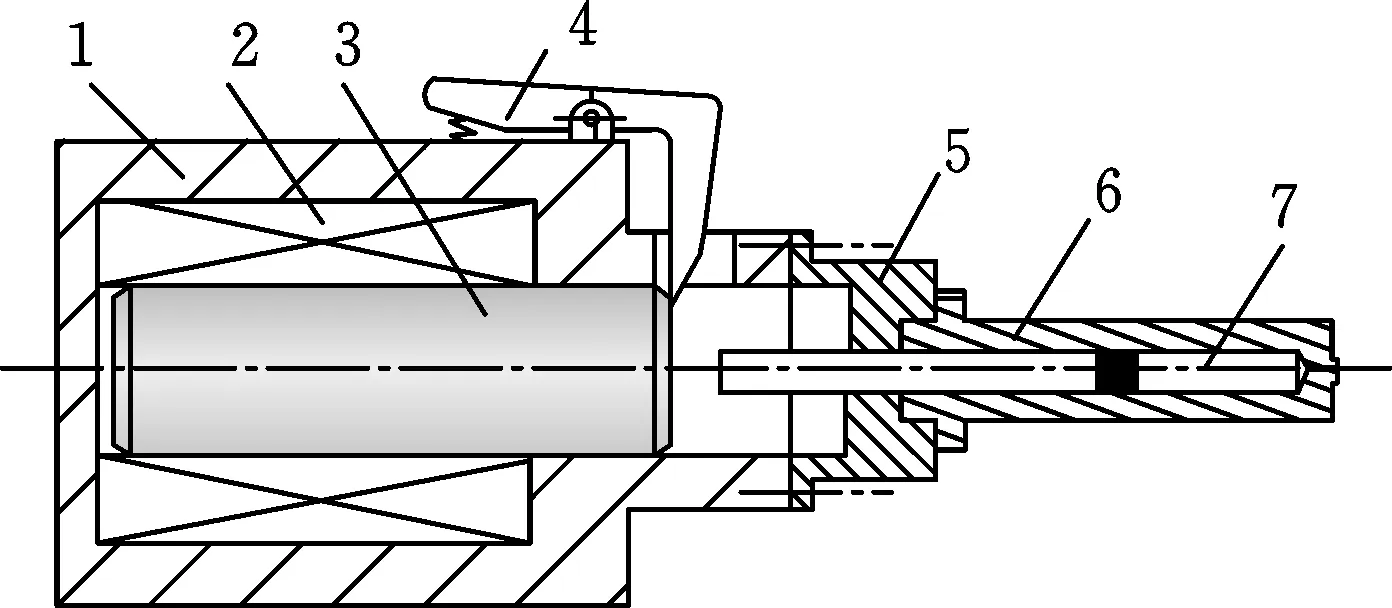
1.缸筒 2.电磁线圈 3.冲击衔铁 4.棘爪机构 5.前端盖 6.无针安瓿组件 7.药液

图2 驱动过程

1.2 驱动系统设计要求

1.2.1线圈

该磁阻式电磁驱动系统电路简化为由电源、电感、电阻的串联电路，通过线圈的电流由于线圈感抗的存在不会立即达到最大值。只有该直流电路达到稳态时，电感才相当于短路，线圈上电压为零，故需要控制无针注射系统中铁心开始运动的时间。

为保证电磁式无针注射系统的稳定性及安全性，选择合适横截面积的铜丝以保证线圈能承受较大的电流，并采用低于36 V(人体安全电压)的直流电压源。

1.2.2铁心

纯铁具有较小的矫顽力，易于磁化和退磁，并具有较好的机械加工性能，故本文选择纯铁作为铁心材料。

1.3 建立驱动力的数学模型

电磁力建模分析之前，对整个电磁线圈做如下简化：忽略线圈受力产生的变形对磁场的影响；忽略铁心在管中运动时与管内壁间的摩擦力，线圈每一截面处的电流密度相等。

由电磁原理推导可得穿过铁心的磁通：

(1)

式中，μ0为真空磁导率；H为磁场强度；A为铁心横截面面积；N为线圈匝数；l为线圈长度；I为线圈电流；x为铁心轴向一点位置(坐标原点位于铁心中心)。

铁心运动过程中，在线圈中的受力大小为

(2)

1.4 Maxwell电磁场仿真

1.4.1驱动系统预仿真分析

为确定无针注射系统相关设计参数大致范围及相互关系，需要对系统进行预仿真分析。在Maxwell软件中设计试验线圈长度l=0.1 m，匝数N=200，外径30 mm，内径18 mm，线圈中电流I=8 A，10 A，12 A，16 A，18A，真空磁导率μ0=4π×10-7N/A2。预设计的铁心长20 mm，直径16 mm，材料为工业纯铁。

将加载电流的线圈作为激励源，设置铁心位置、电流大小为源参数，铁心受力为计算参数。在自适应计算参数设定中，最大迭代次数为5，误差为1%，每次迭代加密部分单元的比例为30%。

(1)电流大小对铁心受力的影响。从图3可知，铁心所受电磁力的大小随通电线圈电流的增大而增大。

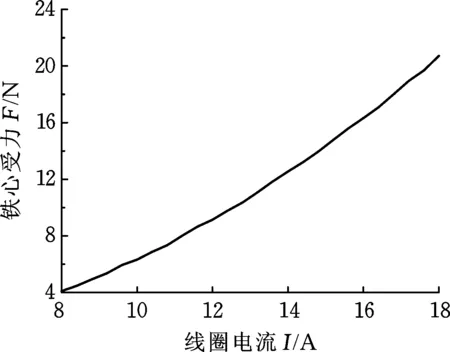
图3 电流大小与铁心受力的关系

(2)铁心位置对铁心受力的影响。从图4可知铁心位置与铁心受力的关系。需要注意的是，铁心中心经过线圈中心后，受到的电磁力为阻力。铁心中心越过线圈中心前，受到的电磁力为驱动力，能获得最优的撞击速度和撞击力度。

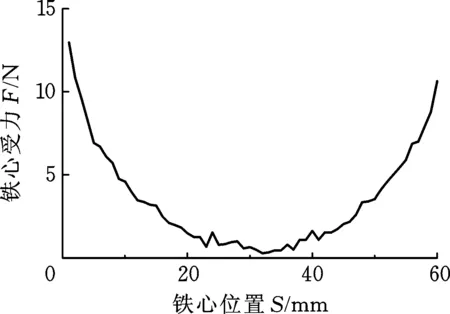
图4 铁心位置与铁心受力关系

(3)铁心长度对铁心受力的影响。设计固定铁心直径16 mm，求解长度不同的铁心在运动过程中的受力。由图5可知，随着铁心长度l1的增大，线圈中气隙的长度减小，磁路磁阻减小，铁心在相同位置的受力增大。

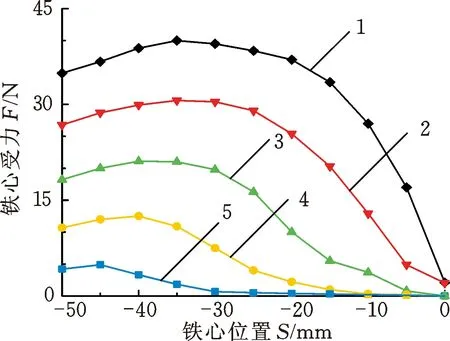
1.l1=20 mm 2.l1=40 mm 3.l1=60 mm 4.l1=80 mm 5.l1=100 mm

(4)铁心直径对铁心受力的影响。设计固定铁心长度60 mm不变，求解不同直径的铁心在线圈内部运动过程中的受力。由图6可知，随着铁心直径d的减小，通过铁心横截面的磁力线减少，空气隙增大，铁心在相同位置的受力减小。

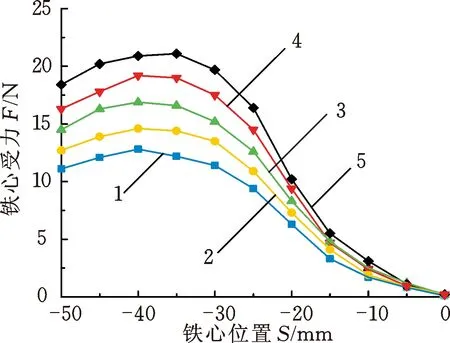
1.d=8 mm 2.d=10 mm 3.d=12 mm 4.d=14 mm 5.d=16 mm

1.4.2磁阻式电磁无针注射系统驱动系统设计与仿真

根据预仿真结果设计无针注射系统驱动系统，设计参数为：真空磁导率μ0=4π×10-7H/m，线圈长度l=0.1 m，线圈安匝数20 000 A·N，线圈内径D1=0.18 m，线圈外径D2=0.4 m，铁心长度l1=0.1 m，铁心直径d=0.16 m。

根据上述参数，在Maxwell软件中建立模型，利用Maxwell自带网格划分工具设置单元格大小，分别对电磁线圈、铁心、作用域进行网格划分。铁心及线圈部分为主要研究对象，对其网格进行密化。设置线圈材料为copper，铁心材料选为iron。

稳定电流通过给定线圈截面时，线圈周围产生磁场，线圈中的铁心会被磁化。铁心与线圈之间的相对位置变化时，磁场中磁场强度H和磁感应强度B不断发生变化，铁心受到的拉力也不断发生变化。

由上述模型，在Maxwell中得到铁心中心相对线圈中心从-50～0 mm处各位置的铁心受力情况，调用pandas库和机器学习库sklearn中的AdaBoostRegressor算法，得到图7所示的不同位置铁心拟合曲线[8]。铁心运动时，-40～-20 mm处的电磁力较为稳定，维持在150 N左右。依据拟合曲线，最终选取铁心中心相对线圈中心位置在-40～-20 mm之间的行程为铁心驱动行程。

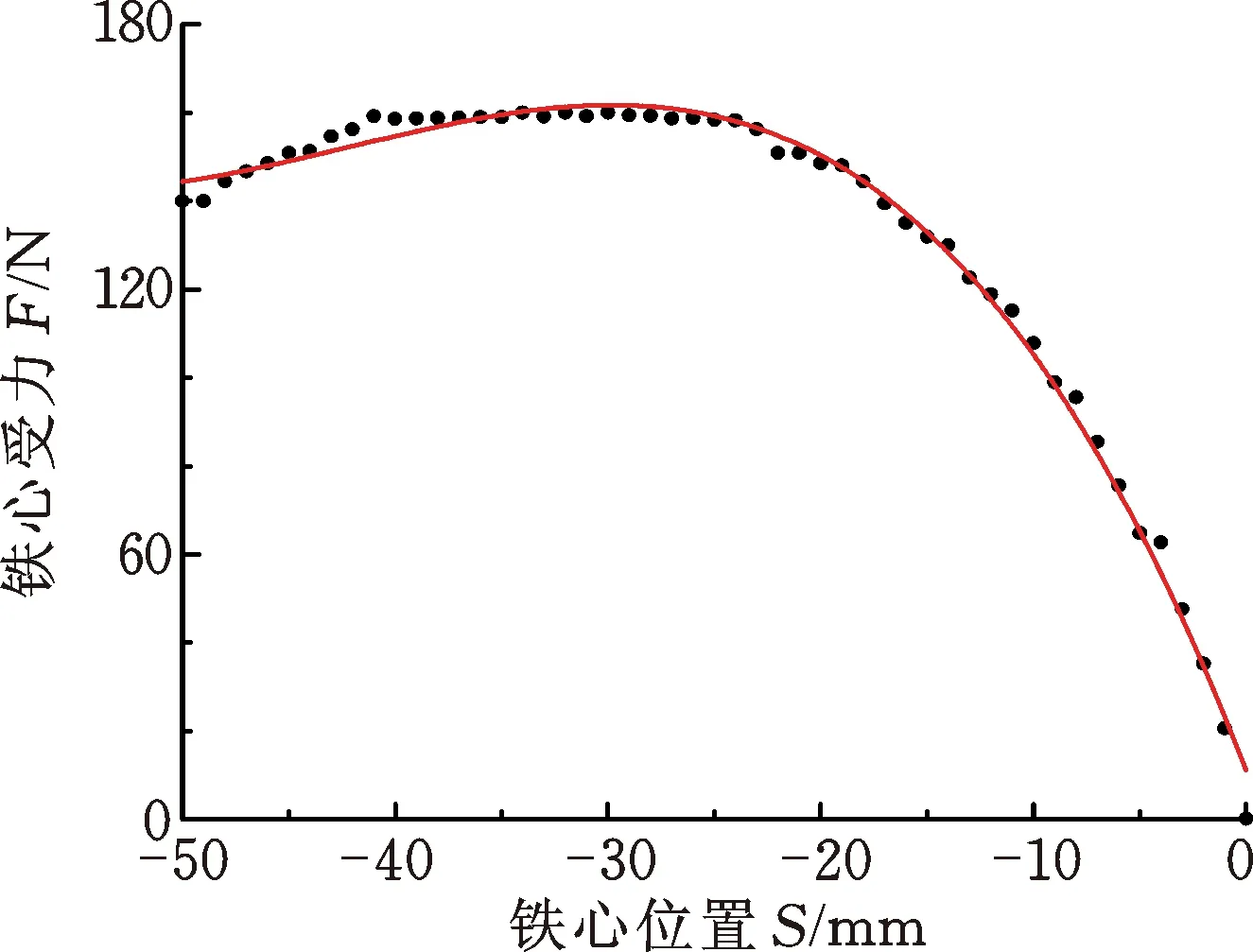
图7 不同位置铁心受力的拟合曲线

2 安瓿喷射模型的建立与仿真

无针注射系统的动力学部分主要集中在安瓿，安瓿将铁心带来的推力转换为药液的高速、高压，以完成药液注射。

2.1 安瓿数学建模

在建模之前，针对安瓿部分做如下简化以便分析：忽略环境温度和药液温度变化对整个系统的影响；设定安瓿瓶为刚性壁面。图8所示为无针注射系统药液部分在喷射过程中的流体模型[9]。

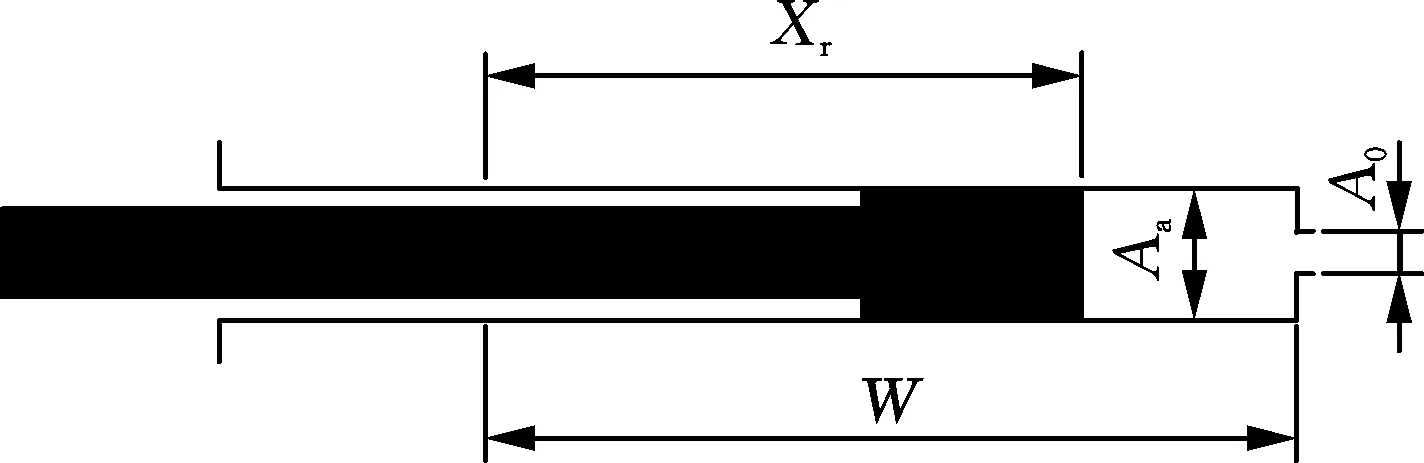
图8 安瓿液流喷射模型

根据质量守恒定律、伯努利方程、牛顿第二定律，并考虑药液的可压缩性、沿程压力损失以及各种能量损耗，得到安瓿内的液体滞止压与安瓿各个参数之间关系：

(3)

式中，Xr为安瓿内活塞杆的运动距离；F为安瓿活塞杆受到的推力；Aa为安瓿腔室的横截面面积；p为安瓿内压力；Ff为安瓿活塞杆橡胶塞与安瓿内壁间摩擦阻力；m为铁心与安瓿活塞杆总质量；E为药液的弹性模量；A0为安瓿前端的微孔横截面面积；ρ0为初始状态时的液体密度；W为初始状态时安瓿腔体内液体总长度。

2.2 数值计算

所设计无针注射系统的基本参数有铁心与安瓿杆质量M=260 g，安瓿杆推力F=150 N，药液体积弹性模量E=2 GPa，安瓿出口面积A0=2.01×10-2mm2，安瓿腔体横截面积Aa=8.9 mm2，沿程摩擦阻力因数为0.0349，安瓿药液初始长度S=30 mm，安瓿腔体内径D=3.36 mm，药液初始密度ρ0=1000 kg/m3，将这些参数代入式(3)，设定药液初始长度为30 mm，电磁线圈的激励条件为安匝数20 000 A·N，安瓿杆受到150 N作用力，可得到1个二元二阶常微分方程，利用MATLAB数值分析可解出压力随时间的变化关系[10-11]。

在药液喷射的初始阶段，压力迅速上升到近29 MPa，然后波动下降，从15 ms开始压力趋于16 MPa，满足设计要求，此时药液注射处于稳定注射阶段；25 ms之后，安瓿射流滞止压消失，此时即可完成药液注射。

2.3 射流仿真

2.3.1射流喷射仿真

无针注射系统所使用的安瓿结构如图9所示，该装置头部有一个直径0.1～0.5 mm的微孔。本文采用尖头安瓿，并对其进行仿真分析。

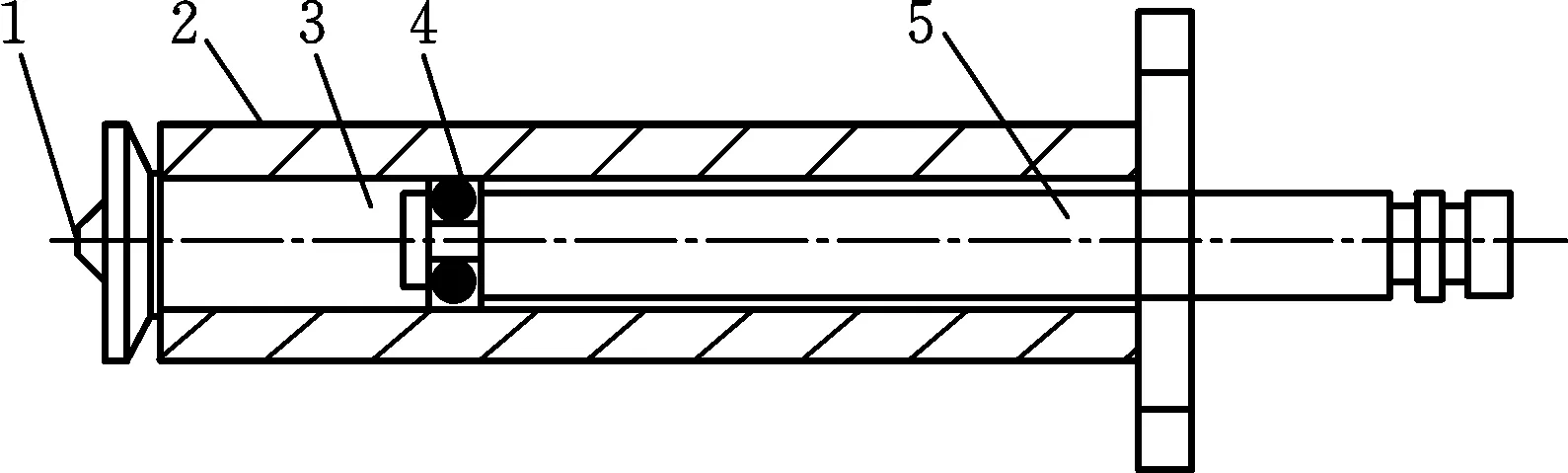
1.安瓿前端微孔 2.安瓿外壳 3.安瓿腔体 4.橡胶密封件 5.活塞杆

(1)模型建立及边界条件。根据实际情况，在ICEM中建立模型，生成四边形非均匀结构化网格。

该尖头安瓿模型前半部分为液体，采用湍流k-epsilon模型(两相流模型)。两相流中的主要物质为空气，水为第二介质。安瓿前面部分为药液区域，内部填充水；后面部分矩形框内为空气区域，内部填充空气。安瓿腔内径取3.36 mm，安瓿前端喷口直径取0.16 mm。设置空气区域前端和上下两端为压力出口，安瓿壁面为无滑移边界且绝热。由此模拟求解安瓿药液喷射速度。

(2)ANSYS数值计算方法。根据此处设置，ANSYS将采用流体连续性方程和动量方程[12]。

连续方程：

(4)

式中，ρa、ρw分别为气相和水相的密度分数；va、vw分别为气相和水相的速度；Sa、Sw分别为气相和水相的质量变化率。

动量方程：

(5)

式中，g为重力加速度；F为两相间相互作用力；μ为有效黏性系数。

(3)仿真结果。图10为采用尖头安瓿设计的射流注射过程图。

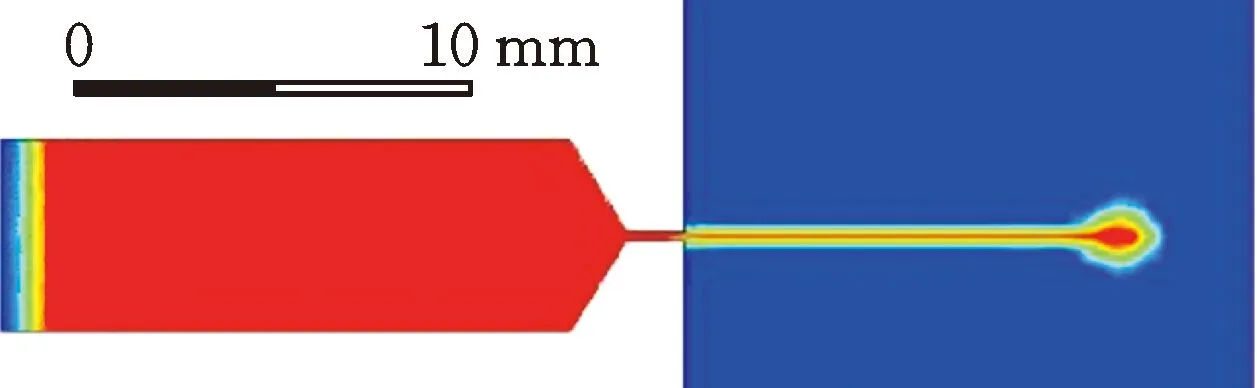
(a) 射流开始

图11为尖头安瓿某一时刻的静压矢量图和速度矢量图。液流经过出射口时，由于两侧斜边的存在，液体压降较为缓和，轴线上的液体基本可以通过安瓿口射出安瓿，避免了大量液流突然聚集的发生。安瓿内的液体汇向出口，靠近出口的液体不断受到后面液体的挤压，尖头与直腔交界处(图11a的圈内)的液体离出射口最远，受到其他液体挤压前进的动力较小，会产生滞留现象，如图11b所示。

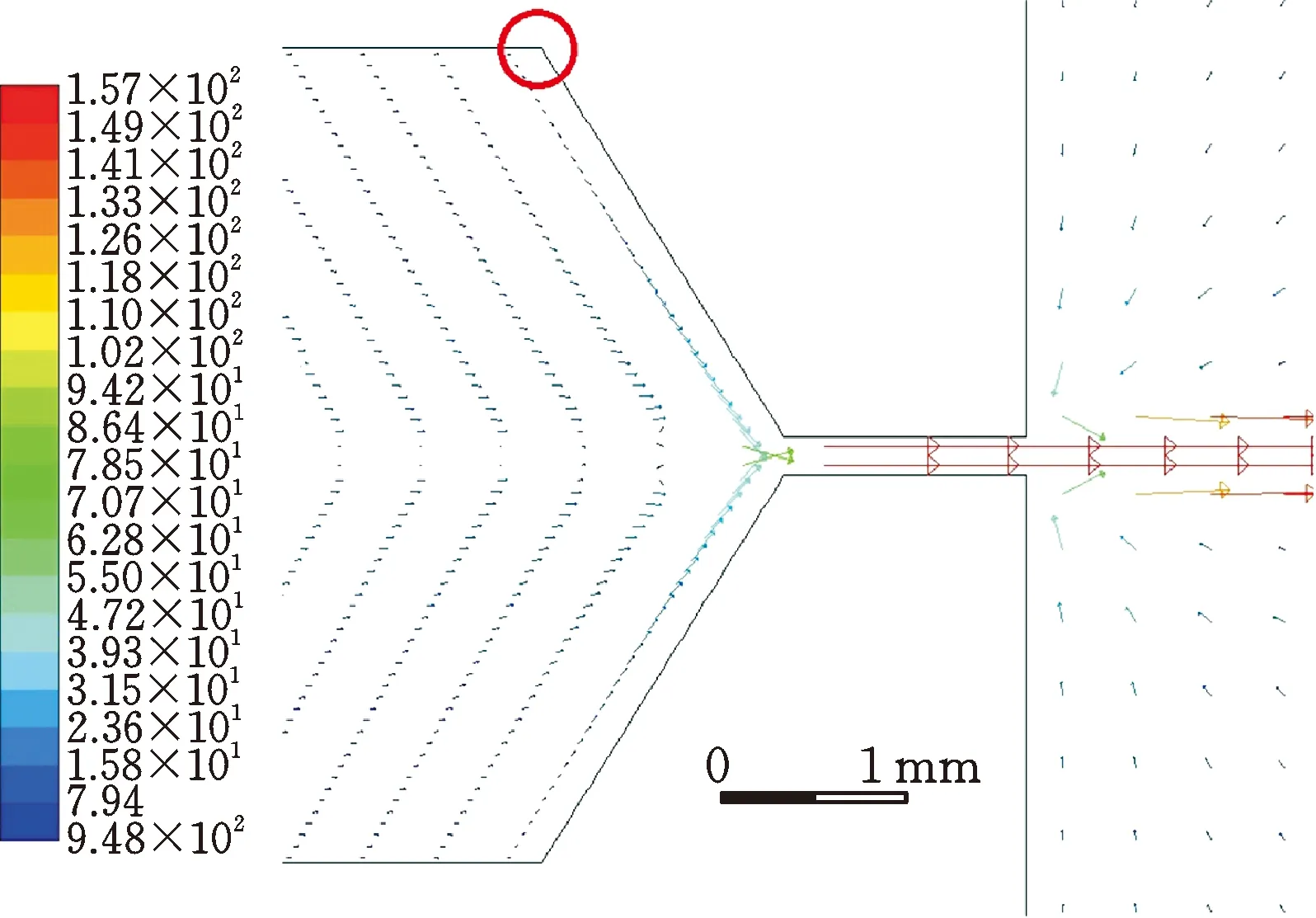
(a) 速度矢量图

图12为尖头安瓿射流某一时刻的轴线压力图和轴线各截面速度图。从图12a可以看出，注射过程中，安瓿内药液的压力接近16 MPa，满足设计要求；安瓿内腔与出射口交界处即圆圈位置基本无负压，所以采用尖头设计的安瓿基本不会出现回流现象。由图12b可以看出，药液射入空气后，药液速度稳定为155 m/s。

2.3.2射流注射仿真

本文研究的是皮下注射过程，在ANSYS中建立皮肤模型(采用多孔介质代替)。安瓿射流模型设置与前文一致。设置多孔介质的黏性阻力系数4×1011，内部阻力系数200[13-14]。

仿真得到的结果如图13所示。由图13可以发现，射流在刺穿皮肤后，在皮肤中扩散开来，形成近似球状的药液扩散区域，注射深度最大可以达到5 mm。

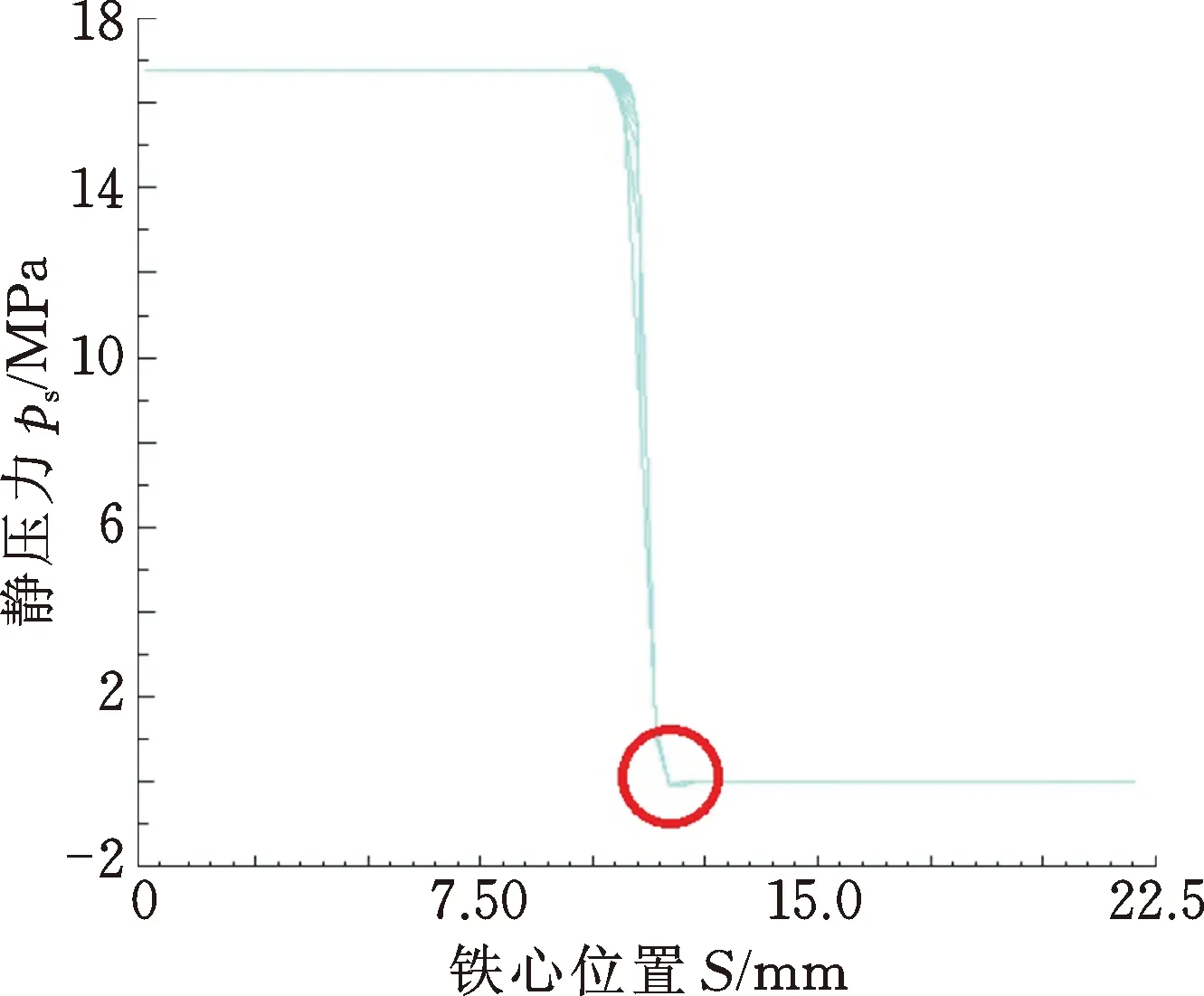
(a) 轴线压力图

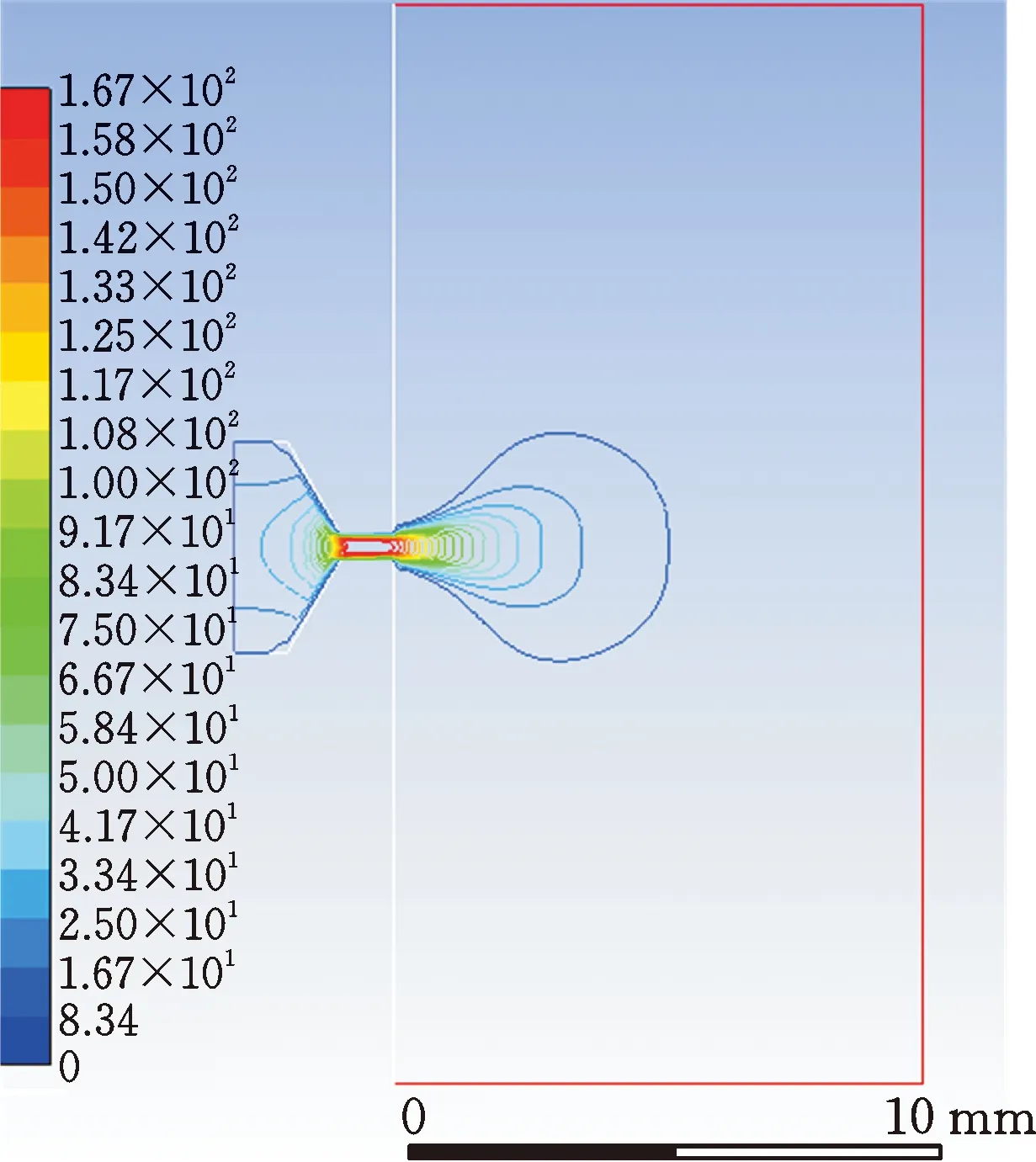
图13 尖头安瓿注射效果

3 平台搭建与实验验证

3.1 实验平台搭建

为验证无针注射装置驱动系统驱动力大小，需设计力测量装置；为验证射流出射速度是否达到药液注射要求，需设计射流速度测量装置。

(1)力测量装置。如图14所示，设计整个实验平台部分为导轨、驱动装置夹具、传感器夹具。采用苏州奥巴特尔自动化设备有限公司的载荷传感器LSZ-F04C测量电磁驱动系统的冲击力。

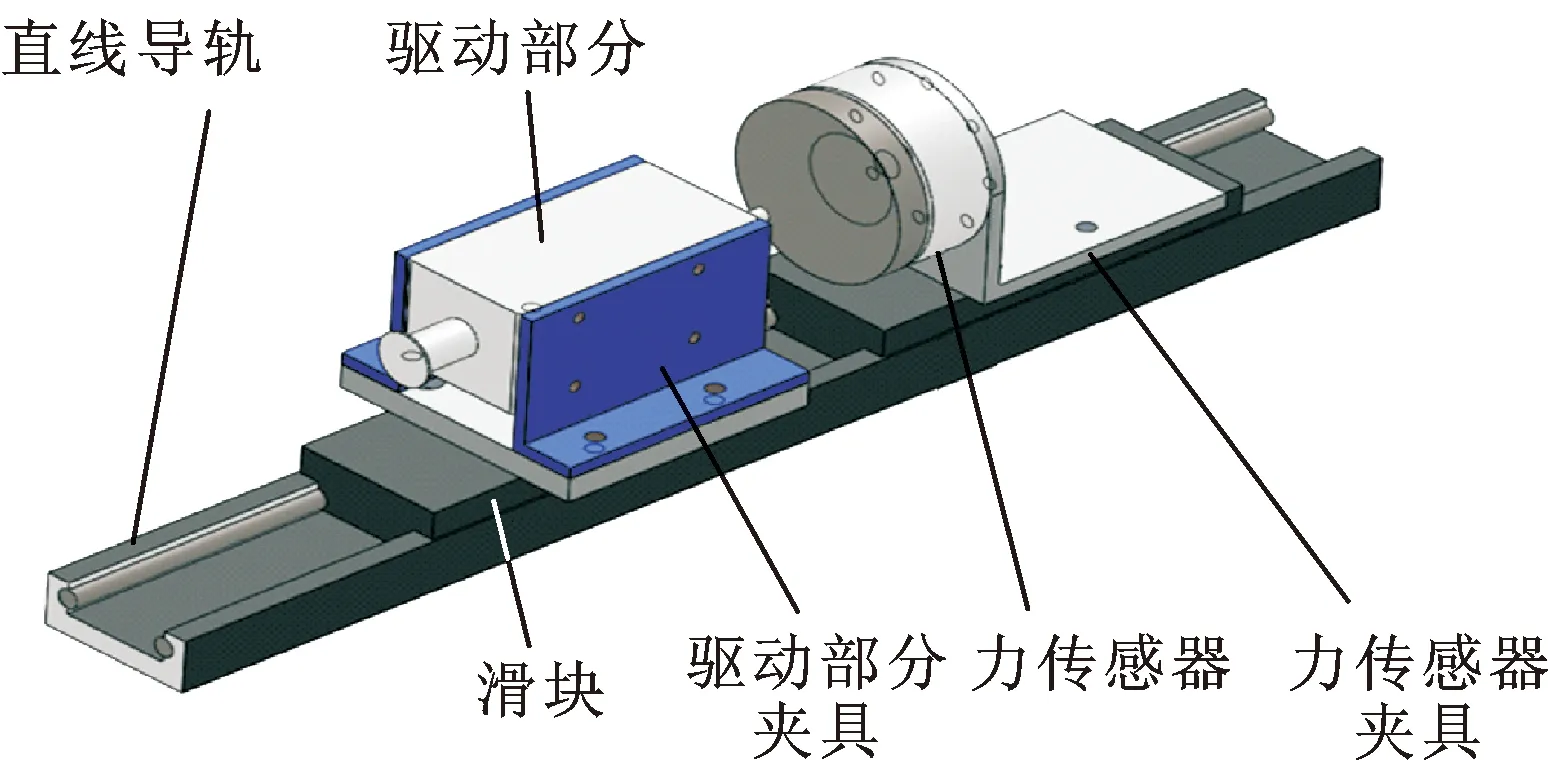
图14 力测量装置

(2)射速测量装置。如图15所示，设计整个实验平台部分为导轨、驱动系统夹具、安瓿夹具。无针注射系统实验平台如图16所示。

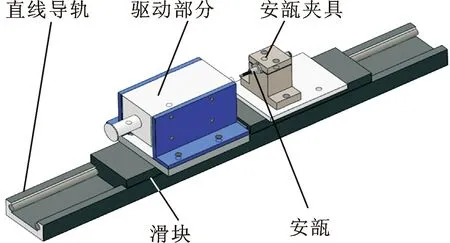
图15 射流流速测量装置

图16 实验平台

3.2 驱动部分实验验证

为验证仿真结果的正确性，利用图17所示的力测量实验平台测量铁心在不同位置处的受力，并将其与仿真结果比较。由图17可以看出，铁心位置在-40～-15 mm之间时，所受的电磁力较为稳定，维持在150 N左右；-15～-5 mm的铁心受力急剧减小；实验结果与仿真结果相仿。

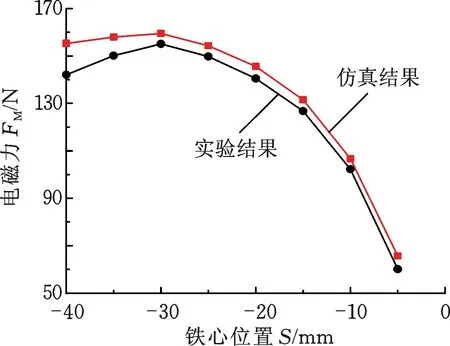
图17 铁心受力实验结果与仿真结果

根据第1节建立的数学模型，由式(2)可知影响驱动力大小的因素有电流、线圈匝数和铁心位置。线圈供电过程中，电压直接影响驱动部分的功率。但由于线圈电感的存在，线圈中的电流不会立即达到最大值。因此，为使驱动效果最佳，线圈获得最大电流并实现蓄能，铁心与安瓿之间需要设置一定的空行程。线圈按照固定匝数制好后，铁心不同位置的受力可从图17得出，故本文研究电流、电压及空行程对驱动力大小的影响。

(1)因素水平的选择。本实验研究的无针注射装置驱动力影响因素主要有电流(A)、电压(B)和线圈中铁心的空行程(C)。在各因素水平合理范围内，安排各影响因素水平，如表1所示。

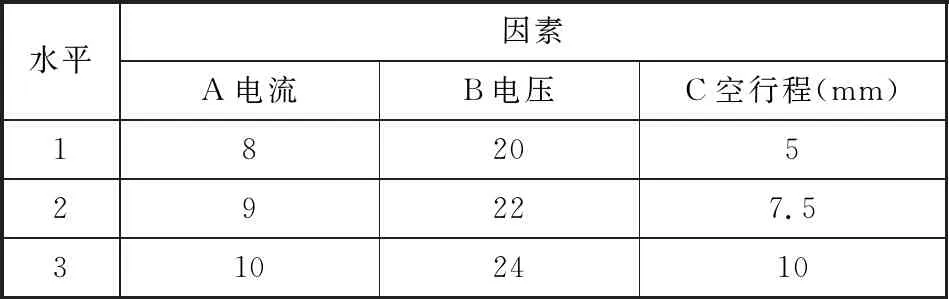
表1 因素水平

(2)正交试验研究。本实验只考虑3个因素，各个因素均取3个水平，安排进行9组实验，以不同因素水平下的药液注射驱动力为优化指标，正交实验要素及实验结果如表2所示。

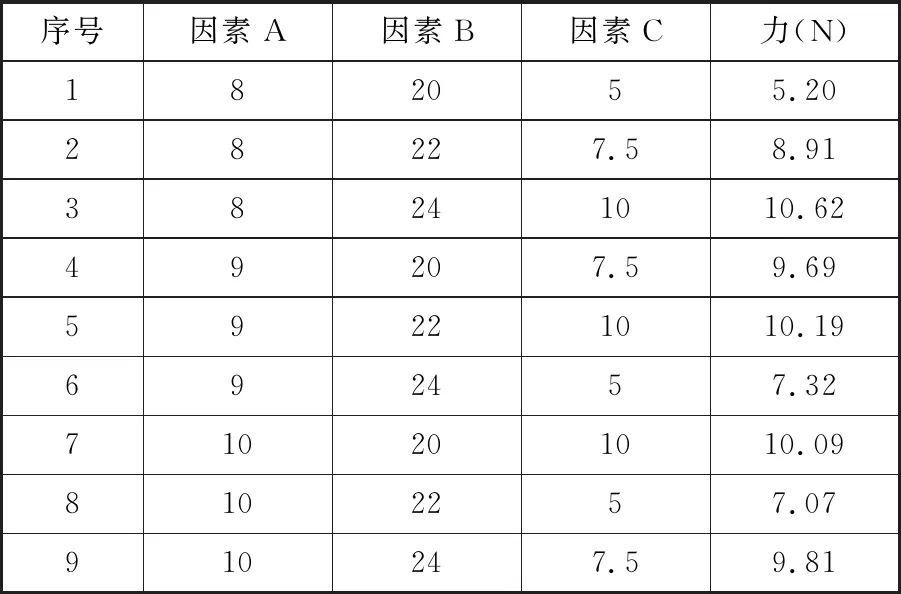
表2 正交试验要素安排及结果

根据正交实验结果，极差分析结果如表3所示。据表3的极差分析结果，比较影响驱动力大小的各因素的极差R，根据R越大、对应因子越主要的原则，得到3个因素对无针注射装置影响顺序为C>B>A，即空行程C的影响最大。由于空行程的存在，铁心在安瓿中运动时存储了一定的能量，即实现蓄能，撞击安瓿活塞杆时，铁心运动动能转换为注射机械能；电流和电压的改变主要影响各个位置驱动力的大小。本组数据中，K1、K2、K3为正交试验的中间变量，以铁心最大

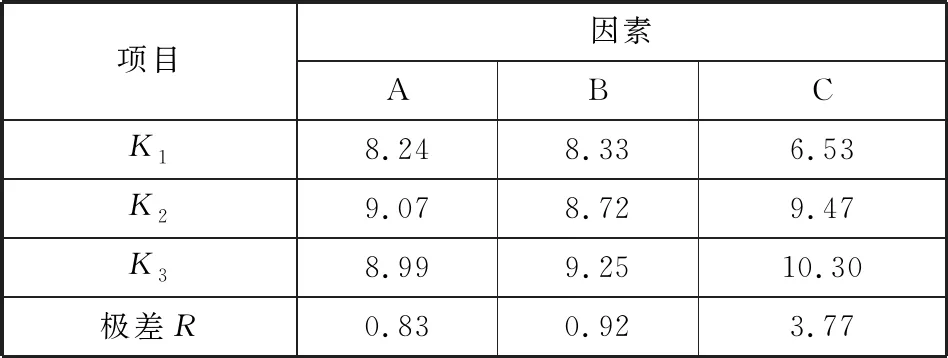
表3 极差分析结果

受力为优化目标时，K1、K2、K3越大越好，驱动力最大的条件为A2B3C3。

3.3 射流速度实验验证

安瓿的液流出射速度超过120 m/s，且药液的注射时间极短(只有几十毫秒)[15]，所以本文采用高速摄影机来观察液流的喷射速度及其与注射时间的关系，并将其与理论结果比较。

3.3.1实验设计

由于相机的拍摄场径内没有标定，看不出每张照片中射流具体移动的距离，所以本实验采用图18所示的纸片作为背景板，在背景板上标出尺度0～60 mm，使安瓿出射口处与标注原点对齐，通过各个图片的比对计算射流速度。设置高速相机帧率为每秒10 000帧，整体实验装置如图19所示。

图18 背景板

图19 高速相机实验设备

由于只能捕捉到射流前端的位置，本实验以液体最外端作为参考点，可求得所需位置处的射流速度：

(6)

式中，S为射流出射距离；Z为设置的高速相机帧率；ni为所需照片的位置；nj为射流初始照片位置。

3.3.2实验分析

图20为安瓿内加满药液(0.3 mL)时，药液喷射的照片。依据式(6)求得各个位置处的速度，如表4所示。从表4可以看出，此时射流速度已经大于120 m/s，满足刺穿皮肤要求和设计要求[16]。

(a) t=0

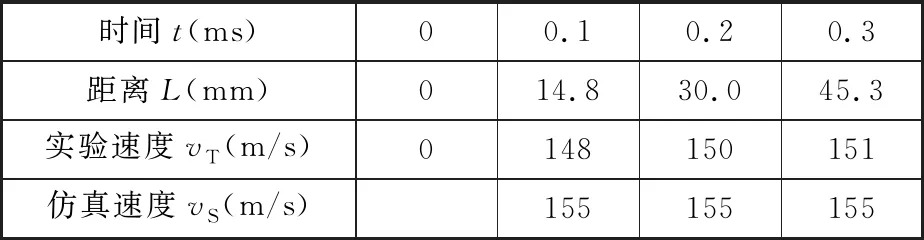
表4 安瓿射流速度

4 结论

本文针对现有无针注射系统驱动力不稳定、体积大、注射效率低、结构复杂等缺点，提出了一种磁阻式电磁蓄能注射器的设计方案，采用空行程蓄能的方式扩大了驱动力的可调范围，使得无针注射装置更易完成注射要求。对驱动部分建模，确定了驱动部分的参数，并进行Maxwell仿真分析；对安瓿部分建模，并进行射流仿真与扩散效果仿真。搭建了实验平台，通过实验验证了无针注射系统理论设计的正确性与可行性。