沪深300股指及期货波动率聚集性研究——基于Markov机制转换SJC Copula模型

罗华健，邹玉梅

(山东科技大学 数学与系统科学学院，山东 青岛 266590)

随着我国由计划经济向市场经济的不断转变，人们的投资观念已经从“传统”变为“现代”。投资者的投资渠道和方式发生了根本性的变化，投资领域逐渐多元化。股票与期货作为投资者的主要投资方式之一，一直影响着投资者的收入。

中国股票市场和中国期货市场一直波动不断。波动率聚集[1]是指金融时间序列的高波动率或低波动率聚集在某一时间段内的现象，即本时间段内为高(低)波动下一时间段也为高(低)波动，后一期波动率与前一期波动率之间是正相关，而且高波动率聚集和低波动率聚集的时期会交替出现。股票和期货收益率序列等金融时间序列往往会出现波动率聚集的情况。波动率聚集能够很好地刻画金融数据本时间段和下一时间段的波动情况。通过对股票与期货的波动率聚集建模进行风险管理与控制成为金融领域的研究热点。

Hamilton[2]首次提出了经过三状态两阶滞后的Markov机制转换模型，并利用该模型研究了美国1953—1984年季度实际产出增长的波动，该模型能较好地刻画金融数据的非线性动态特征和非对称性。Chang等[3]比较详细地介绍了机制转换模型的应用。随后Markov机制转换模型被应用到经济、金融等多个领域，显示出优于传统非线性时间序列模型的许多特点。近年来，许多学者将Markov转换模型运用到股票与期货市场。Lee[4]运用Markov机制转换Gumbel-Clayton Copula GARCH模型对农产品期货市场套期保值进行研究，指出该模型能够更加有效地估计套期比率。Pelletier[5]和Klassen[6]对股票收益率序列进行研究，Markov机制转换Copula GARCH模型能更好地刻画股票收益率序列间相关性的非对称性。Chollete等[7]和Luo等[8]运用多变量状态转换Copula模型对市场收益进行研究，表明机制转换Copula模型能更好地对证券风险进行评估。学者[9-11]运用机制转换跳跃模型对纽约铜期货进行研究，发现铜期货收益率跳跃在牛市和熊市存在显著性差异。学者[12-14]运用机制转换Copula模型对股市间的相关性进行研究，结果表明机制转换Copula模型更能刻画股市间的相关性，且股市间存在不同的相依状态。谢赤等[15]和陈之星等[16]使用MRS Copula-GJR-Skewed-t模型和机制转换Copula函数研究了期货市场的套期保值，表明Markov 机制转换Copula函数的套期保值可以获得比传统模型更高的收益，且有助于降低套期保值的成本。吴吉林等[17]运用机制转换混合Copula模型对股市量价尾部关系进行研究，量价尾部关系与机制状态有关，呈明显的周期性动态特征和结构性变化。杨孟阳等[18]运用机制转换GARCH模型对中小板市场的收益率波动性进行研究，证明中小板市场股指收益率确实存在明显的高低两种波动状态，且低波动状态的持续时间更长。淳伟德等[19]运用机制转换混合Copula模型对期货与现货尾部相关性进行研究，机制转换混合Copula模型更能准确地描述两个市场之间的尾部相关性，且上尾相关性要大于下尾相关性。吴鑫育等[20]运用Markov机制转换Copula模型对沪深股市的波动率聚集性进行研究，发现沪深两市的波动率聚集存在两种状态。

综上所述，学者[4-20]在建立模型时，假定市场处于两状态或三状态下，研究金融市场的微观结构，并没有给出相对应的实际市场，无法判断是否与实际市场相吻合。多数学者[4-19]只是研究单一经济市场，研究多个市场的经济状况的成果相对较少。

本研究通过构建两、三状态Markov机制转换SJC Copula模型来刻画沪深300指数和股指期货的t-1时刻和t时刻之间的波动率聚集的尾部非对称、动态特征，比较两市场尾部可能存在的差异。与其他动态Copula模型相比，Markov机制转换SJC Copula模型具有更好的数据拟合效果，并且该模型更易于实现。同时，得到的机制转换Copula模型的平滑概率图与实际市场相对应，对加深对金融市场微观结构的理解，为投资者和风险管理者提供信息和决策参考。

1 Markov机制转换Copula模型

1.1 模型构建

波动率聚集性是金融资产收益率序列中的一个重要特征，在期货与现货市场也不例外。而Copula模型可以充分捕获连续波动变量的相关性(波动率聚集性)。设xt和xt-1分别代表t和t-1时刻沪深300指数和股指期货收益率的波动率，利用xt和xt-1的联合分布函数H(xt,xt-1)来刻画波动率聚集性。根据Sklar[21]定理，存在一个Copula函数C(·,·):[0,1]2→[0,1]，使得

H(xt,xt-1)=C(F(xt),F(xt-1)|θ)。

(1)

其中，F(xt),F(xt-1)分别为xt,xt-1的边际分布函数；θ为Copula函数的参数向量。

金融数据的相关性通常是非线性的，并可能随时间变化，从而引起市场波动。因此使用动态非线性Copula模型来研究非线性动态相关性，条件尾部相关系数在极值理论中被广泛应用，即当极值在一个观测变量出现时，极值出现在另一个变量的概率。连续波动率变量xt和xt-1的上尾和下尾的相关系数分别为:

(2)

(3)

其中，当λU,λL∈(0,1]时，说明xt和xt-1存在上尾或下尾相关性；当λU或λL等于零时，说明xt和xt-1不存在上尾或下尾相关性。可以用不同的Copula函数来刻画不同的尾部相关性结构。两类常用的Copula函数为椭圆Copula函数和阿基米德Copula函数。第一类主要有Normal Copula函数和Student-t Copula函数，只能描述尾部对称性特征；第二类主要有Clayton Copula函数、Gumbel Copula函数和Frank Copula函数。其中Clayton Copula函数只能刻画下尾部相关性，Gumbel Copula函数只能刻画上尾部相关性，Frank Copula函数不能刻画尾部相关性。连续波动率变量可能同时具有上尾和下尾相关性，且呈现非对称特性。由于Student-t Copula函数比Normal Copula函数具有更厚的尾部，对变量间尾部相关性更为敏感。近年来，一些学者[17,19]使用混合Copula函数描述了金融数据的尾部相关性，取得了良好的效果。因此，本研究采用Student-t Copula函数和混合Copula函数来拟合沪深300指数和股指期货连续波动率变量存在的尾部特征。

构建Clayton Copula函数和Gumbel Copula函数组成的混合Copula函数，表达式如下

CCG(u1,u2|θ)=ωCCC(u1,u2|δC)+ωGCG(u1,u2|δG)。

(4)

其中，CC(u1,u2|δC)和CG(u1,u2|δG)分别为Clayton Copula函数和Gumbel Copula函数，ωG+ωC=1。

SJC(Symmetrized Joe Clayton)Copula函数也可以同时捕获上尾和下尾相关性，允许非对称的上尾和下尾相关性，并且包含对称的尾部相关性。经过修正后的Joe-Clayton Copula函数得到的即为SJC Copula函数，其中Joe-Clayton Copula函数的分布函数为

(5)

SJC Copula函数的表达式为

CSJC(u1,u2|λU,λL)=0.5(CJC(u1,u2|λU,λL)+CJC(1-u1,1-u2|λU,λL)+u1+u2-1)。

(6)

当λU=λL时，SJC Copula函数是对称的。

Student-t Copula函数、混合Copula函数和SJC Copula函数的尾部相关特征如表1。

表1 各Copula函数的尾部相关性特征

由于静态的Copula函数假设相关性参数不是时变的，因此无法捕获连续波动性变量之间可能存在的尾部动态特征。为了描述尾部相关性的动态特征和可能的结构变化，本研究将状态变量St引入到Copula函数中，并假定St={1,2,3}遵循一个一阶三状态的Markov过程，状态转移概率矩阵如下:

(7)

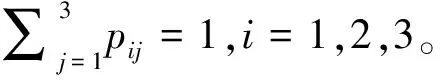
对于三状态机制转换Copula函数，设

(u1t,u2t|St=i)～C(u1t,u2t|θi),i=1,2,3。

(8)

最后，可以依据得到的转换概率计算某一种状态持续的平均时间。假设D为机制i的持续时间，因此:

D=1，如果St=i且St+1≠i，Pr[D=1]=1-pii；

D=2，如果St=St+1=i且St+2≠i，Pr[D=2]=pii(1-pii)；

⋮

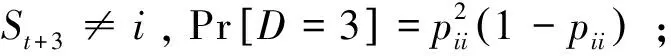
那么，机制(状态)i持续的平均时间为:

Classification of occurrence form of spheric weathered granite and stability analysis LIU Zhi-jun, WANG Xian-neng, MO Li(40)

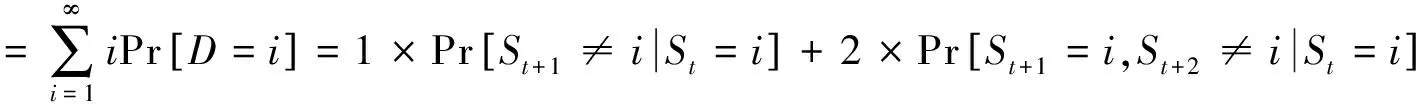
+3×Pr[St+1=i,St+2=i,St+3≠i|St=i]+…

(9)

1.2 参数估计

1.2.1 Copula模型的参数估计

第一阶段，采用半参数两阶段的估计方法。利用非参数核估计方法估计出沪深300指数和股指期货波动率的边缘分布。核估计结果的优劣主要取决于核函数和窗宽。当样本数目足够大时，核函数的选取对估计结果影响不大，因此选取光滑性良好的正态核函数。其密度函数和分布函数表达式如下:

(10)

(11)

其中，x=(x1,x2,x3,…,xN)为样本数据，N为样本量，h为窗宽。

对于具有尖峰、厚尾性质的金融时间序列，利用Bowman等[22]提出的最优窗宽选择原理进一步得到最优窗宽

(12)

(13)

第二阶段，将第一步估计得到的边缘分布代入Copula函数中，并对Copula函数进行相应的参数估计，估计出Copula函数的参数α。

(14)

1.2.2 机制转换模型的参数估计

采用Hamilton提出的滤波过程来估计机制转换Copula模型的参数(本研究以两状态为例，三状态机制转换模型可以根据两状态情形推广)。具体过程如下。

1)设定初始值，即状态1或2的无条件期望值。

(15)

(16)

其中s0为初始状态变量，I0为初始信息集。

2)计算预测概率

(17)

3)计算机制转换SJC Copula模型的概率密度函数

(18)

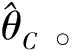
(19)

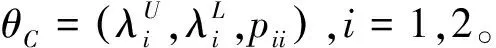
5)计算过滤概率

(20)

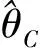
2 实证研究

选取沪深300指数和沪深300股指期货当月连续合约日内5 min高频交易价格作为研究样本。当月连续合约相比于在股指期货的其他三个合约，由于当月连续合约的交易量最大，因此能够更准确地刻画股指期货的整体走势。考察的时间段为2014年1月4日—2016年12月19日。对于缺失数据，采用均值替换法进行处理，共得到721个样本值，如图1。

图1 沪深300和股指期货已实现波动率序列图

因为金融市场不能直接地观测到波动率，所以选取的隐波动率的代理变量为通过日内5min高频交易数据构建的已实现波动率。令n为日内收益率总数目，rt,i=100(lnPt,i-lnPt-1,i)为t交易日的第i个日内对数收益率。则将一天的累计日对数收益率的平方和作为日波动率的估计值，即第t交易日已实现波动率定义为

(21)

假设沪深300指数和股指期货波动率序列随时间连续变化、波动率在一个固定范围内变化(即波动率是平稳的)以及观测到的收益率不会被市场微结构噪声“污染”，令σ2(t)为波动率过程，已实现波动率依概率收敛于积分波动率(Integrated Volatility，IV)，

(22)

刘红忠等[23]采用交叠样本法和ARMA-GARCH模型研究沪深两市上的晚间休市对股票收益率的影响。研究表明沪深两市均存在持续稳定的“隔夜效应”，因此为了避免“隔夜效应”带来的对真实波动率的影响，令rt,0=100(lnPt-1,n-lnPt,0)为隔夜收益率，对已实现波动率进行修正：

(23)

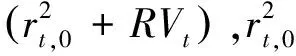
表2给出了沪深300指数和股指期货已实现波动率的描述性统计量的值。由于现货市场每日的开盘时间上午9：30—11：30，下午13：00—15：00，每日的5 min数据有48个；而期货市场的每日开盘时间上午9：15—11：30，下午13：00—15：15，每日的5 min数据有54个。所以股指期货已实现波动率的均值、最小值、最大值等描述性统计量要比沪深300指数大。从表2可以看出，沪深300指数和股指期货的已实现波动率均呈现出正偏(4.453 7>0，5.080 7>0)，存在尖峰、厚尾的特征(24.207 4>3，31.555 8>3)，并都拒绝正态分布的假定(JB统计量显著)。

表2 描述性统计量

表3给出了Student-t Copula函数、混合Copula函数和SJC Copula函数的参数估计的结果。从混合Copula函数和SJC Copula函数的相关性估计结果来看：沪深300指数和股指期货指数上尾相关性均大于下尾相关性，即沪深300指数和股指期货波动率高波动率的聚集要比低波动率的聚集发生的概率要高。本研究选用Joe[25]提出的基于Copula函数的AIC信息准则:AIC=-2ln(L)+2K，其中ln(L)代表Copula概率密度函数的极大似然值，K代表Copula函数中的参数个数。从三种Copula函数的极大似然估计值和AIC的值来看，混合Copula函数和SJC Copula函数的极大似然值均大于Student-t Copula函数，AIC值均小于Student-t Copula函数。其中，SJC Copula函数具有最大的似然值和最小的AIC值，说明SJC Copula函数具有最好的拟合效果。由SJC Copula函数的拟合数值可以知道，股指期货高波动率聚集相比沪深300指数高波动率聚集发生的概率要高，而低波动率聚集发生的概率沪深300指数更高一些。

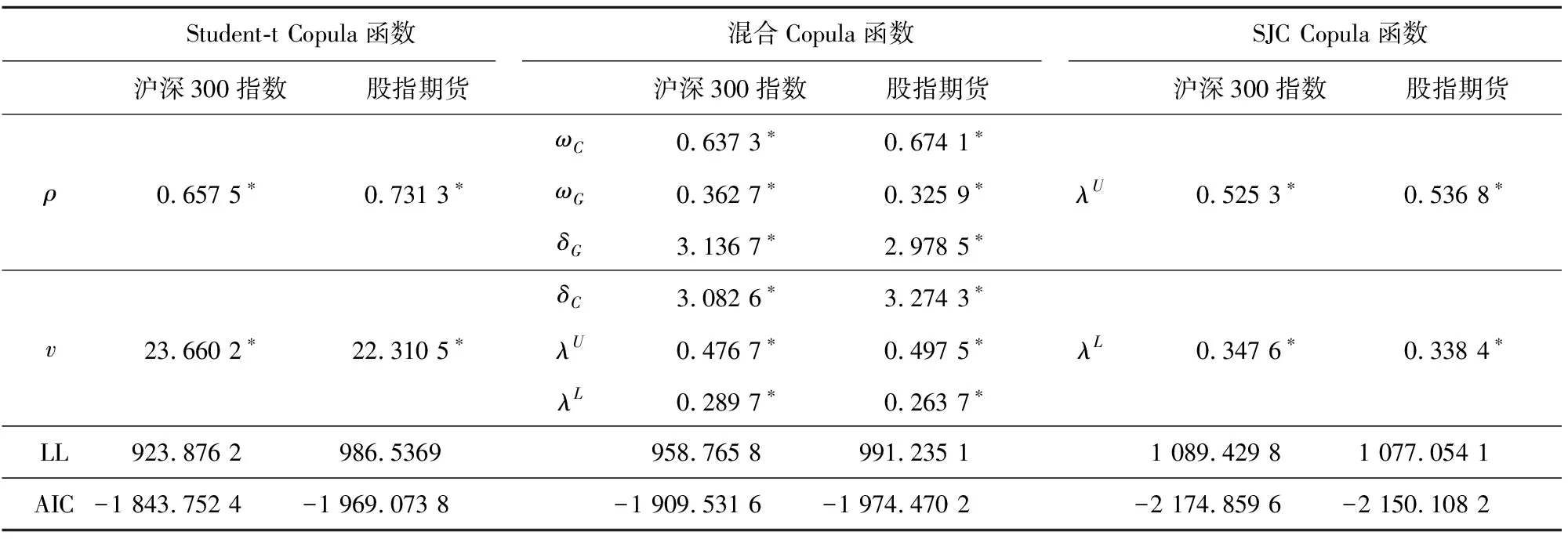
表3 Copula参数估计结果

选取对波动率具有最佳拟合效果的SJC Copula函数来构建Markov机制转换Copula函数模型，以分析沪深300指数和股指期货波动率聚集可能存在的尾部动态特征。表4给出了极大似然估计方法得到的机制转换SJC Copula函数参数估计结果。从极大似然估计值和AIC值来看，经过机制转换后的SJC Copula函数比机制转换前的有更大的似然值和更小的AIC值，说明机制转换后SJC Copula函数比机制转换前的拟合效果更优，并且三状态机制转换比两状态机制转换具有更大的似然值和更小的AIC值，说明三状态机制转换比两状态机制转换具有更优的拟合效果。在三种状态机制转换SJC Copula模型下，沪深300指数和股指期货的上尾相关系数均明显大于下尾相关系数，与机制转换前得出的结论一致。当St=1时，沪深300指数上尾相关系数明显小于股指期货上尾相关系数，但沪深300指数的下尾相关系数大于股指期货上尾相关系数。当St=2时，沪深300指数的上尾相关系数明显小于股指期货的上尾相关系数，而沪深300指数和股指期货的下尾相关系数相差0.018。当St=3时，沪深300指数的上尾相关系数明显大于股指期货的上尾相关系数，但下尾相关系数明显小于股指期货的下尾相关系数。

表4 Markov机制转换SJC Copula模型参数估计结果

表5给出了沪深300指数和股指期货三种状态的相关系数。表6给出了沪深300指数和股指期货三种状态之间的转移概率和持续期。从表5和表6可知，状态1的转移概率、持续时间和相关系数最大，状态2次之，状态3最小。说明在三状态下，对于沪深300指数和股指期货高波动率聚集的持续时间均大于低波动率聚集的持续时间。图2给出了沪深300指数和股指期货三种状态的平滑概率图。从图2可知，三种状态的平滑概率曲线与实际经济市场相对应。2014年1—6月，受IPO(首次公开募股)重启、沪港通试点和“新国九条”发布的影响，经济有所好转，股市及期货市场处于状态2(经济复苏阶段)。2014年7月—2015年6月，十八届三中全会后，我国全面启动深化体制改革。在国际社会上，美国宽松货币政策全面从我国市场上退出，间接地刺激了我国金融市场的发展，各行业百废待兴，市场处于状态1(经济平稳发展阶段)。2015年7—12月，分级基金去杠杆、场外配资清理和场内融资形成了金融市场上的连锁反应，最终引起了一场长达半年的股灾，我国股票市场和期货市场萎靡不振，市场处于状态3(经济低迷阶段)。该阶段由于信息到达速度快、频率高，尾部非对称性明显增强，上尾相关性参数值明显大于下尾，高波动率聚集相比低波动率聚集发生的概率更高。2016年1—12月，受熔断机制、减持新规、人民币贬值和推行注册制等因素的影响，经济有所回暖，市场处于状态2(经济复苏阶段)。

表5 沪深300指数和股指期货三种状态的相关系数

表6 沪深300指数和股指期货三种状态之间的转移概率和持续期

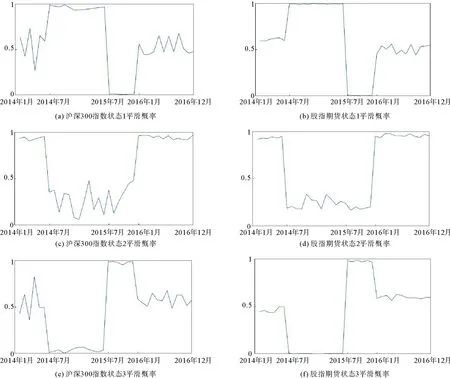
图2 沪深300指数和股指期货平滑概率

为了得到沪深300指数和股指期货的波动率聚集的尾部动态过程，引入Hamilton算法，其上、下尾动态过程表达式如下

(24)

(25)

其中It-1为t-1时刻的信息集。图3给出了沪深300指数和股指期货的尾部动态。从图3中可以看出，沪深300指数和股指期货的波动率聚集的尾部存在明显的动态特征。

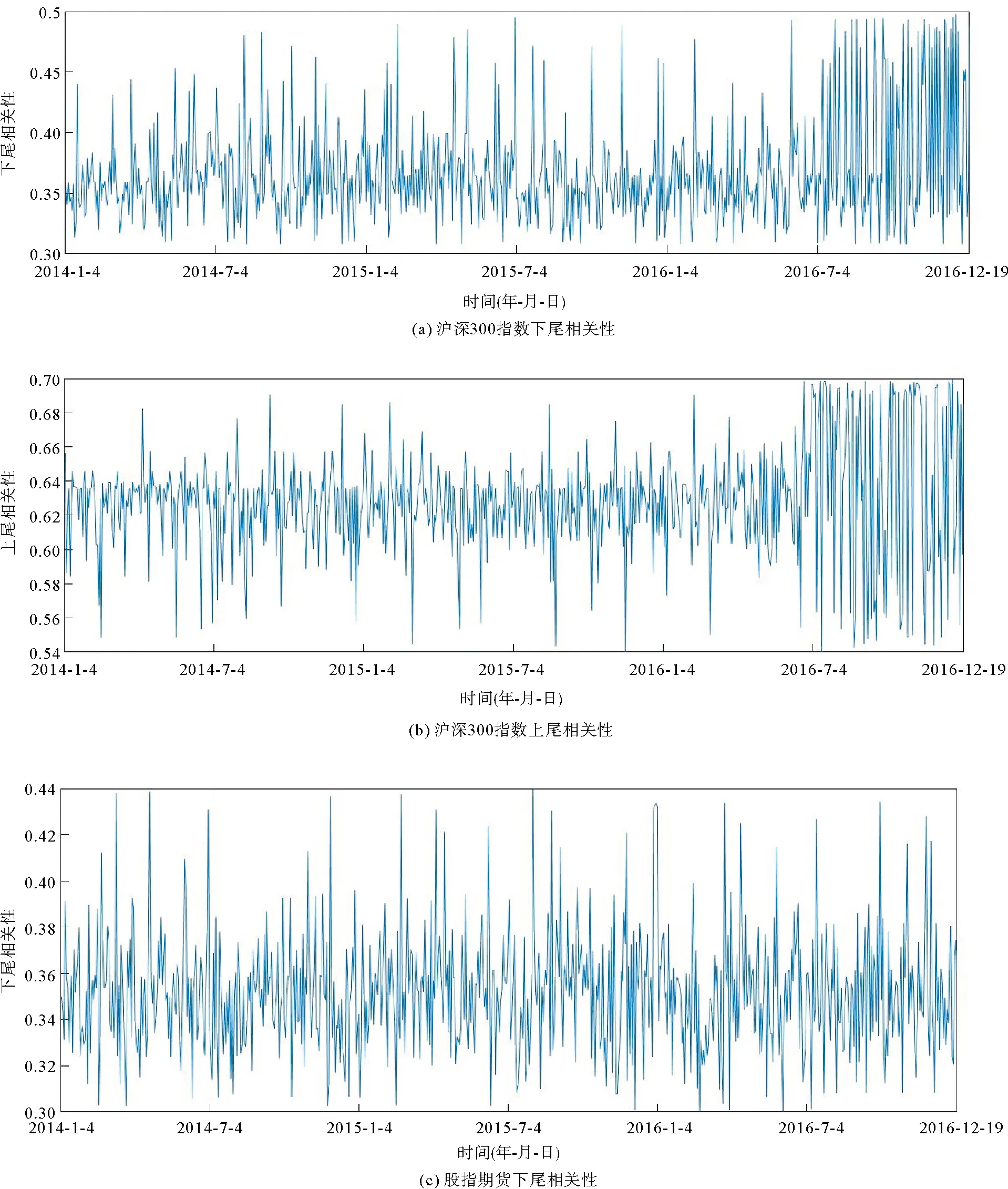
图3 沪深300指数和股指期货的尾部相关性

3 结语

金融市场的波动率聚集一直是金融界理论研究的重要内容，运用本时间段的金融市场的波动情况来预测未来的波动情况，是投资者和风险管理者进行分散投资风险和进行风险管理需要考虑的关键点。在本研究中，把沪深300指数和沪深300股指期货当月连续合约日内5min高频交易价格作为样本，运用Markov机制转换SJC Copula模型对沪深300指数和股指期货的波动率聚集尾部动态特征进行研究。研究表明：①与其他Copula模型相比，机制转换SJC Copula能更好地拟合金融数据波动率聚集的尾部动态特征；②波动率聚集的尾部具有明显的非对称性，上尾相关性明显大于下尾相关性；③在三状态下，高波动率聚集的持续时间均大于低波动率聚集的持续时间。另外，在针对波动率聚集的研究中，由于股价受隔夜效应、午间效应、周末效应等因素的影响，采用的修正的已实现波动率并不能充分地反映股价波动情况，在后续的研究工作中，将进一步完善充实。