带约束分数阶正系统稳定性与镇定的判定和计算的一个新方法
司新栋,杨洪礼
(山东科技大学 数学与系统科学学院,山东 青岛 266590)
分数阶微积分是对整数阶微积分的推广。分数阶正系统是指具有非负状态的分数阶系统,在许多问题中,由于其能直观刻画绝对温度、能级、高度、浓度等[1-2],能够更准确描述工程问题,因此近年来分数阶正系统的研究得到更多工程人员的关注[3-4]。相比较而言,整数阶正系统的研究结果比较多:文献[5-9]对整数阶正系统基本问题,如正性、可控性、客观性、可达性等进行了研究;文献[10-11]基于代数方法对正系统稳定性进行研究;文献[12-13]得到了正系统稳定的充分条件,并将其化为二次规划问题;文献[14]得到了正系统稳定的充分必要条件,把稳定性条件转化成线性矩阵不等式问题;文献[15-17]得到了正系统稳定的充分必要条件,把稳定性条件表示成线性规划问题;文献[18]提出了一种利用状态反馈控制求解闭环系统稳定问题的方法。
然而,对于分数阶正系统而言,上述问题的研究结果却不多。特别是对带有状态和控制约束的工程问题,系统的稳定性是需要满足的先决条件,是控制系统能够正常运行的前提[19],所以研究该问题具有实际意义。由于分数阶积分定义形式的特殊性,传统整数阶系统的稳定性结论和研究方法不能直接应用于带有控制和状态约束的分数阶系统[20],因此,带约束的分数阶系统的稳定性研究是必要的。
本研究利用线性规划方法研究带控制约束的分数阶系统的稳定与镇定问题。从Metzler矩阵理论和分数阶线性系统稳定性理论出发,针对系统为不确定系统、状态非负有上界约束和控制非负有上界约束三种情况,利用线性规划得到状态反馈控制律,进而使得分数阶线性系统保持稳定性与正性并且满足约束条件。得到一类新的求解连续分数阶系统稳定性与正性控制的线性规划方法。该方法简单可行,对于维数较高的问题也比较容易实现,数值实验表明此方法稳定,能提高状态反馈控制求解效率,是一个比较有吸引力的方法。
文中符号的具体说明如下:Rn表示n维实向量空间,Rn×n表示n×n维实矩阵的集合,x(t)表示系统状态向量,u(t)表示系统控制向量,AT表示矩阵A的转置,E表示单位矩阵,O表示零矩阵,0表示零向量,x>0或x<0表示向量x的每一个分量xi>0或xi<0。bi表示矩阵B的第i行向量;bi(k)表示对应矩阵B(k)的第i行向量;y(i)∈Rm(i=1,2,…,n)表示m维列向量。
1 引言
考虑连续分数阶线性系统
(1)
其中:A∈Rn×n,B∈Rn×m为系统状态矩阵,x(t)∈Rn为系统状态向量,u(t)∈Rm是系统控制向量。
定义1[21]令α为分数阶导数的阶,则关于x(t)的Riemann-Liouville分数阶导数定义为
(2)
其中,Gamma函数为
(3)
定义2[21]令α为分数阶导数的阶,则关于x(t)的Caputo分数阶导数定义为
(4)
根据定义1与定义2,得到Caputo分数阶导数与Riemann-Liouville分数阶导数关系为
(5)
定义3[22]设A=[aij]∈Rn×n,若aij≥0(i≠j),则A为Metzler矩阵。
定理1[23]系统(1)为正的充分必要条件是矩阵A为Metzler矩阵。
根据定义3和定理1,系统(1)为分数阶正系统的充分必要条件是矩阵A中的非对角线元素非负,即aij≥0(i≠j)。
下面给出无控制约束条件下系统(1)的稳定性与镇定问题。
定理2[23]若存在一个Lyapunov 函数和一个class-k函数βi,i=1,2,3,满足
其中α∈[0,1],则系统(1)是渐进稳定的。
引理1[23]对于连续分数阶正系统
(6)
函数V(x(t))=λTx(t),λ>0为Lyapunov 函数的充要条件是A是Metzler矩阵且Aλ<0。
由定理2与引理1得到定理3。
定理3[23]系统(6)渐进稳定的充分必要条件是存在一个向量λ>0,使得Aλ<0。
若存在一个状态反馈控制u(t)=Kx(t),使得系统(1)对应的连续分数阶系统
(7)
渐进稳定,则系统(1)能镇定。
定理4系统(7)具有渐进稳定性和保持正性的充分必要条件是矩阵A+BK为Metzler矩阵且(A+BK)λ<0。
证明:存在一个状态反馈控制u(t)=Kx(t)使得系统(1)中A=A+BK,B=O,得到系统(7)。
充分性:矩阵A+BK为Metzler矩阵,根据定理1,系统(7)具有正性。又由于(A+BK)λ<0,根据定理3,系统(7)具有渐进稳定性。
必要性:系统(7)具有正性,根据定理1,矩阵A+BK为Metzler矩阵。由于系统(7)具有渐进稳定性,A+BK为Metzler矩阵,根据定理3,(A+BK)λ<0。
2 主要结果
工程问题中,系统或状态存在约束是常见的现象。文献[24]采用传统Ziegler-Nichols方法进行分数阶控制器设计,Luo等[25]基于相位裕度、幅值裕度及参数鲁棒稳定性条件,开展了分数阶控制器设计和数值计算方法的研究。上述研究成果都是基于频域的线性系统分数阶控制器设计,若以状态空间形式描述线性系统,并要求满足不同的控制任务,则以上控制器并不适用。为确保不同的控制目标得以实现,需要设计不同内容形式的控制器对被控系统加以控制。
本节将对分数阶系统(1)为不确定系统(uncertain)、状态非负有上界约束、控制非负有上界约束三种情况进行讨论,寻找状态反馈控制u(t)=Kx(t),使得系统(7)保持稳定和正性,进而系统(1)能镇定。受文献[23]启发,根据定理4,将该问题转化为线性规划问题进行求解。
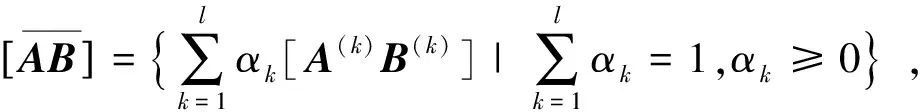
(8)
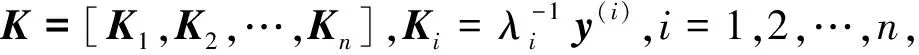
(9)
(A(k)+B(k)K)λ<0,k=1,2,…l,λ>0。
(10)
由于λj>0,对于i≠j有
(11)
根据式(10)、式(11)得到存在一个状态反馈控制u(t)=Kx(t),使得每一个A+BK矩阵为Metzler矩阵且(A+BK)λ<0,进而根据定理4得到系统(7)具有稳定性和正性。

(12)
根据(A+BK)λ<0得到
(13)
根据式(12),式(13)得到线性规划(LP1)。
引理2[26]系统(6)任意初始条件0≤x0≤x,有0≤x(t)≤x的充分必要条件是(A+BK)x<0。
根据引理2及定理4得到如下定理。
定理6当系统(1)中状态非负且有上界约束xmax,即0≤x(t)≤xmax时,则系统(7)保持稳定和正性的充分必要条件是存在一个状态反馈控制u(t)=Kx(t),满足下列线性规划问题
(14)
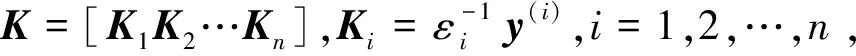
(15)
(A+BK)ε<0,ε>0,
(16)
由于εj>0,对于i≠j,有
(17)
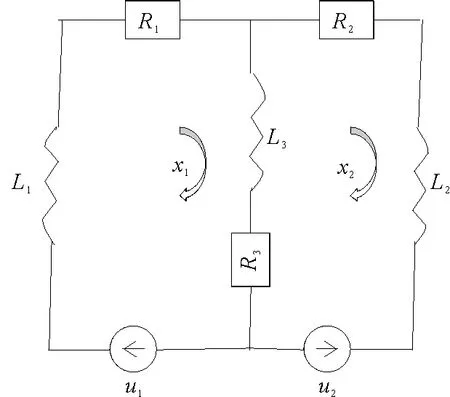
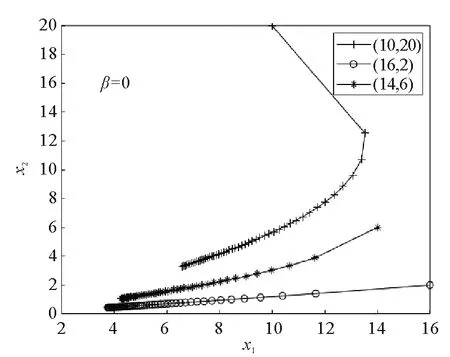
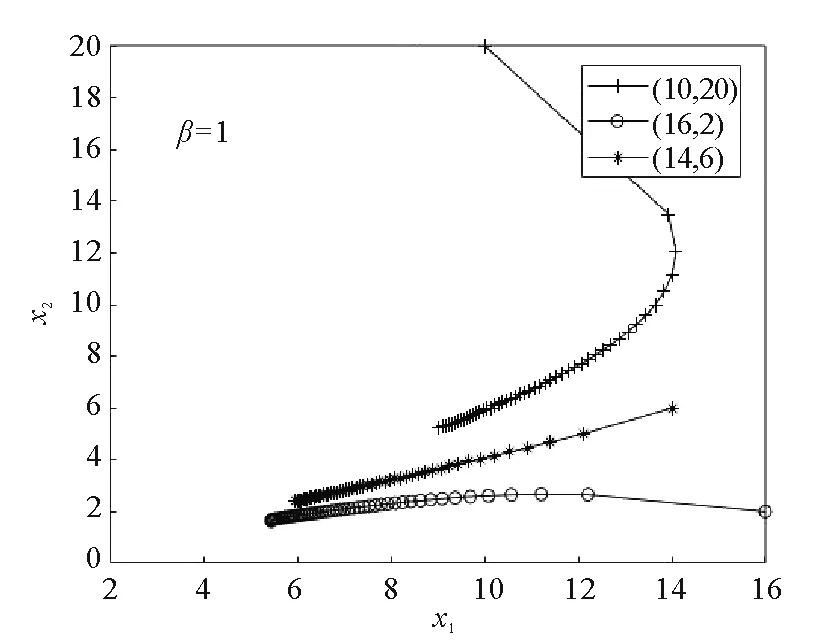
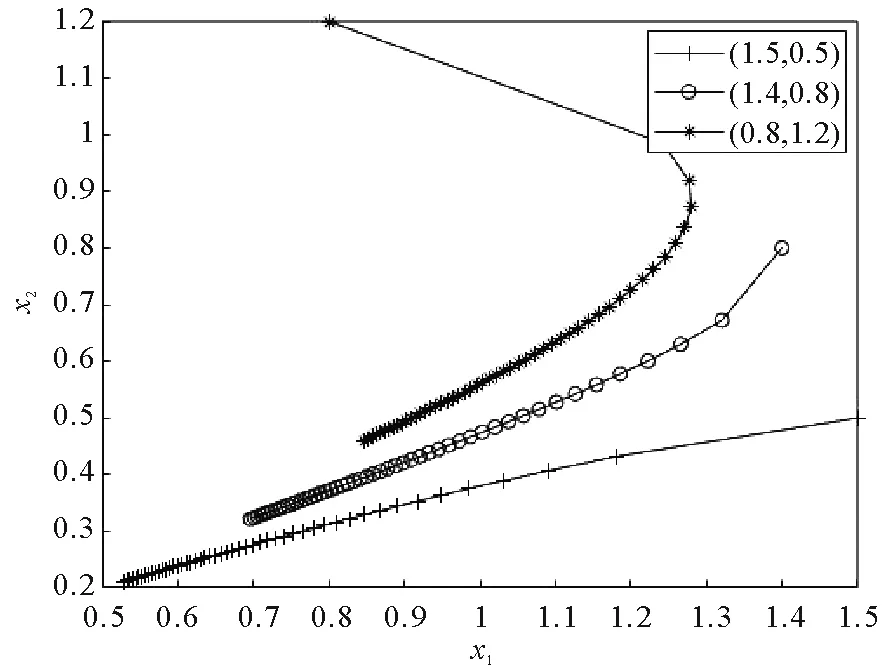
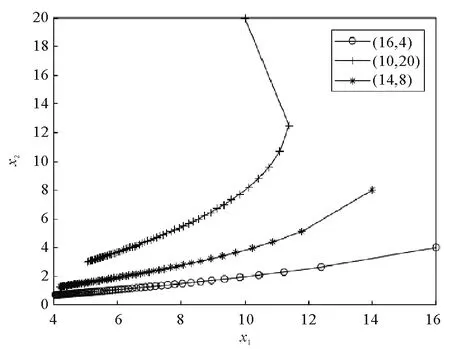
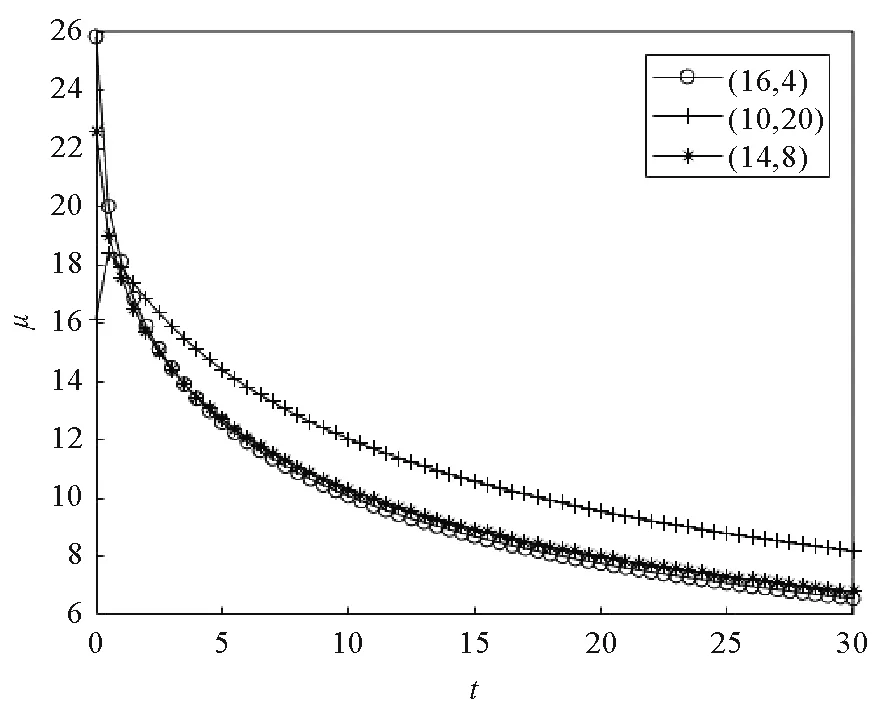
A+BK矩阵为Metzler矩阵且(A+BK)ε<0。根据引理2,对于0 0≤x(t)≤ε≤xmax。 (18) 根据式(16)和式(17)得到存在一个状态反馈控制u(t)=Kx(t),使得每一个A+BK矩阵为Metzler矩阵,且(A+BK)ε<0,进而根据定理4得到系统(7)具有稳定性和正性。根据式(18)得到满足条件0≤x(t)≤xmax。 必要性:系统(7)具有稳定性和正性,根据定理4得到存在一个状态反馈控制u(t)=Kx(t),使得每一个矩阵A+BK为Metzler矩阵且(A+BK)ε<0。由引理2,0≤x0≤ε时,有0≤x(t)≤ε。当ε>xmax时,有x(t)>xmax,与状态非负有上界矛盾,所以0<ε≤xmax。式(14)中第一个与第三个不等式证明同定理3,进而得到线性规划(LP2)。 (19) (20) (A+BK)x<0,x>0, (21) 由于xj>0,对于i≠j,有 (22) 所以A+BK矩阵为Metzler矩阵且(A+BK)x<0。 数值实验通过MATLAB软件得出,实验结果均四舍五入保留四位小数。 考虑分数阶R,L,u型电路,其中R1,R2,R3是电阻,L1,L2,L3是电感,u1,u2是源电压,x1,x2是线圈里的电流。电路如图1所示。 图1 R,L,u形式电路图 根据电路图得到分数阶R,L,u型电路系统为 例1考虑分数阶R,L,u型电路系统,当电感或者电阻变化时,系统为不确定系统且含有不确定因素β(0≤β≤1),其中A,B表示如下 根据定理5,结合线性规划不等式组 正性判定:通过状态反馈控制得到新的系统(7),当β=0时,矩阵 根据例1,当β=0时,对于不同的初始条件(10,20),(14,6),(16,2),新系统的状态轨迹如图2所示,当β=1时,对于不同的初始条件(10,20),(14,6),(16,2),新系统的状态轨迹如图3所示。 图2 例1系统状态轨迹图 图3 例1系统状态轨迹图 其中,时间步长为0.1 s,总时长为50 s,并且Mittag-Leffler指数函数中的k=400。状态轨迹在第一象限均收敛到(0,0),表明新系统从随机选取的非负初始条件演化而来,新系统具有稳定性。 根据定理5,当系统为不确定系统,即矩阵A,B含有不确定因素,可以利用线性规划求出一个状态反馈控制使新系统保持正性与稳定性。 例2考虑分数阶R,L,u型电路系统,电路需要满足条件为线圈里的电流非负有上界即0≤xi(t)≤2,i=1,2,其中A,B表示如下: 根据定理6,结合线性规划不等式组 正性判定:通过状态反馈控制得到新的系统(7),矩阵 矩阵A+BK为 Metzler矩阵,得到系统(7)具有正性。 根据例2,对于不同的初始条件(1.5,0.5),(1.4,0.8),(0.8,1.2),新系统的状态轨迹如图4所示。其中,时间步长为0.1 s,总时长为150 s,并且Mittag-Leffler指数函数中的k=400。状态轨迹在第一象限收敛到(0,0),表明新系统从随机选取的非负初始条件演化而来,新系统具有稳定性。 图4 例2系统状态轨迹图 根据定理6,当原系统状态非负有上界时,可以利用线性规划求出一个状态反馈控制使新系统具有正性和稳定性,且新系统的状态非负有上界。 例3考虑分数阶R,L,u型电路系统,电路需要满足条件为源电压非负有上界即0≤μi(t)≤30,i=1,2,其中A,B表示如下 根据定理7,结合线性规划不等式组 根据例3,对于不同的初始条件(16,4),(10,20),(14,8),新系统的状态轨迹如图5所示。 图5 例3系统状态轨迹图 其中,时间步长为0.1 s,总时长为30 s,并且Mittag-Leffler指数函数中的k=400。状态轨迹在第一象限收敛到(0,0),表明新系统从随机选取的非负初始条件演化而来,新系统具有稳定性。 相应的控制轨迹如图6所示。 图6 例3状态演化轨迹图 可以看出,对μ的限制满足条件。 根据定理6,当原系统控制非负有上界时,可以利用线性规划求出一个状态反馈控制使新系统保持正性和稳定性,且新系统的控制非负有上界。 主要研究了带约束的连续分数阶系统的稳定性与正性的一个判定与求解方法。首先得到连续分数阶线性系统为正系统和渐进稳定的一个充要条件,然后将求解带控制约束的连续分数阶系统状态反馈控制问题转化为一类线性规划问题,最后通过求解线性规划得到满足所给约束条件的控制律,使得闭环系统保持稳定性与正性并且满足控制约束条件。通过该方法可以得到使闭环系统保持稳定性与正性并且满足控制约束条件的控制律,符合实际工程的应用。同其他方法相比,该方法易于数值实现。数值实验表明,该方法正确可行且方便求解,提高了求解效率。在后续的研究中,将针对状态空间描述的一般形式的分数阶线性系统以及分数阶非线性系统,进行稳定性与正性控制研究。




3 数值例子
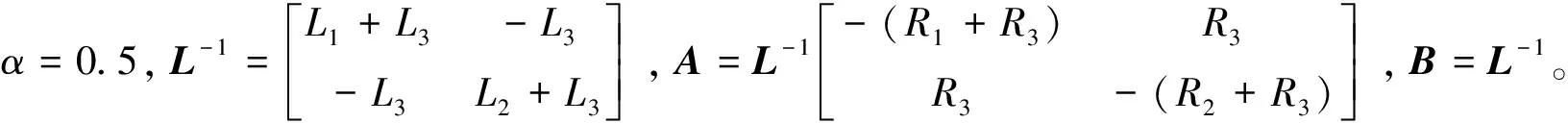

4 结论

