基于Evacuation NZ疏散模型火灾人员疏散时间研究

2021-02-24 01:43惠工程师韦晓璐

安全 2021年1期

郭惠工程师韦晓璐

(北京市西城区消防救援支队，北京 100032)

0 引言

随着社会发展和科技进步，现代建筑呈现多样化、复杂化、大型化特征，这些特征为消防安全工作带来新挑战，如一些超高层异形、人员密集的建筑很难确定最大人员承载量、火灾时疏散人员的最佳疏散口位置及所需疏散时间等。因此，在发生火灾等突发事件时，如何有效进行人员疏散是值得深入研究的问题。

1977年，加利福尼亚大学建筑生命安全小组的Larslerup提出“绘图手则”，它奠定分析火灾中人员行为动态的基础；1996年，中国香港城市大学S.MLO收集整理部分火灾逃生人员的数据信息，并在此基础上构建一个可预测火场受困人员反应的模型，以研究火灾时被困人员心理对人员疏散的影响。随着计算机技术的发展，人们开发多种疏散软件和模型用来分析建筑物内人员疏散特性，如Stahl开发的BFIRES-II模型、美国Francis开发的预测最小理论疏散时间的EVACNET+模型等。目前人员疏散模型有30个左右，如常见的Building EXODUS和SIMULEX，这些模型较系统，有各自的参数和适用范围，但应用性不强，仅供科研人员借鉴进行二次研究。Evacuation NZ疏散模型可以根据需要及时调整疏散过程中人员的行为，并可以在特定情况下利用连接密度计算疏散时间，为相关部门对疏散时间进行估算提供参考。

1 计算机模拟方法

运用计算机模拟方法研究火灾人员疏散问题，通常有2类方式：第一类是在仅考虑火灾疏散人员运动轨迹的基础上建立模型；第二类是在既考虑火灾疏散人员运动轨迹，又考虑人员行为的基础上建立模型。第一类参数相对确定，主要是建筑内部消防设施、疏散人员速度、疏散出口位置和方向等，它虽然简单直观，但没有考虑人员个体差异，所有人都被设定按统一要求进行疏散，这种不考虑人员个体行为差异的模型称为“滚珠”模型；第二类是在第一类基础上，除考虑可确定因素，还把每个人的个体差异融入其中，全面考虑火灾疏散人员个体差异对疏散时间的影响。这种模型能更真实地模拟火灾疏散人员的反应以及疏散时间。

火灾中人员的疏散行为复杂，每个人的疏散行为由于个体差异而不同。因此，研究火灾疏散人员的疏散行为，既要考虑人的心理因素，也要考虑在特殊环境下人的社会行为因素。综上，要建立适合复杂多变情况的模型，需要综合考虑建筑物、人和环境的相互影响等因素，而传统人工计算方式很难做到如此巨量运算和数据处理。因此，计算机因其计算功能强大、模拟过程逼真等特点在疏散模拟方面体现出其优势。

(1)可选定计算机模拟软件中的不同算法对火灾中人员疏散时可能发生的不同情景进行分析评估，这种评估有数据支撑，算法也可以不断优化，不受人的主观因素影响，因此评估更加客观准确。

(2)计算机模拟可以研究疏散过程中的特殊现象，分析人员疏散过程中的运动规律，找出影响疏散时间的关键因素。

(3)计算机模拟可以全程直观地观察人员的行动轨迹，并得到人员疏散的细节，分析影响疏散时间的因素，从而可在设计阶段提供更直接有效的消防安全设计方案。

(4)在建筑物设计过程中，通常都使用比较简单的方法来计算人员疏散时间，这种计算方法没有考虑人员行为对疏散时间的影响。选择合适的计算机模拟软件，通过二维或三维渲染技术以及人体模型移动处理技术来实现人员在紧急状态下避难、逃生等活动。同时，消防监督执法部门对建筑物开展安全性评估时，也可以把计算机模拟软件的模拟过程当作评估依据和衡量指标。

2 Evacuation NZ疏散模型

2.1 背景

Evacuation NZ疏散模型是坎特伯雷大学在Evacent 4疏散软件基础上开发出的疏散模型。Evacent 4疏散软件将疏散人群看作一个整体，未考虑个体在疏散过程中的行为差异。而Evacuation NZ疏散模型可以随时改变任意疏散人员的行为文本，而不需要重新设置数据，更接近于真实疏散过程。Evacuation NZ疏散模型把人员密度分为连接密度和节点密度，并将他们作为研究疏散时间的参数，并结合Monte Carlo得出疏散时间分配的可能性。Evacuation NZ疏散模型在模拟时不限制人和节点数量，如果计算机运算能力足够强，就可模拟足够多的人和节点，因此，此模型适合模拟计算超高层、复杂建筑中的人员疏散时间。

2.2 节点密度和连接密度

Evacuation NZ疏散模型把人员密度分为节点密度和连接密度，如图1。

节点密度是一个节点的平均人员密度，是由一个房间的人数和地板面积决定(人员密度

=人数

/地板宽

·地板长

)。当人群涌向出口，连接密度逐渐增加，节点密度没有变化，当连接密度达到特定值时出口变得拥挤，此时连接密度通常要高于节点密度。

图1 节点密度和连接密度Fig.1 Node density and connection density

连接密度可能会随人员年龄和周围环境变化而不同，且在紧急情况下由于人群拥挤，连接密度高于非紧急情况。Nelson和Maclennan认为人员密度的最大值是3.5ppl/m，而Pauls认为连接密度的最大值是2.0ppl/m。

2.3 人流速率

运用Evacuation NZ疏散模型模拟计算疏散时间是基于Nelson和Maclennan的流体运动方程。

(1-0.266

)

(

)

(1)

式中：

—人流速率，ppl/min；

—人员密度，ppl/m；

—建筑构件实际宽度，m；

—边界层的厚度，m；

—速度系数，为建筑构件的函数。

对于门：取84，一侧的边界层取0.15m；

对于楼梯：

=51.8·(

)

(2)

式中：

—楼梯踏步的宽度，m；

—楼梯踏步的高度，m。

2.4 疏散时间

利用Evacuation NZ疏散模型模拟疏散时间，在疏散总人数不超过500人，疏散门宽度不超过1.6m的模拟结果，如图2。通过改变连接密度和疏散门宽度(确保疏散门宽不超1.6m的情况下)，发现当连接密度为2.2ppl/m，无论疏散门宽度为多少，模拟的疏散时间与通过流体运动方程计算时间都位于对角线上，即当连接密度为2.2ppl/m时Evacuation NZ模型模拟数值最接近于流体运动方程计算所得数值。所以，消防监督员日常监督检查过程中或建筑单位内部组织疏散演练不方便时，可以通过该连接密度利用流体运动方程估算建筑物疏散时间。

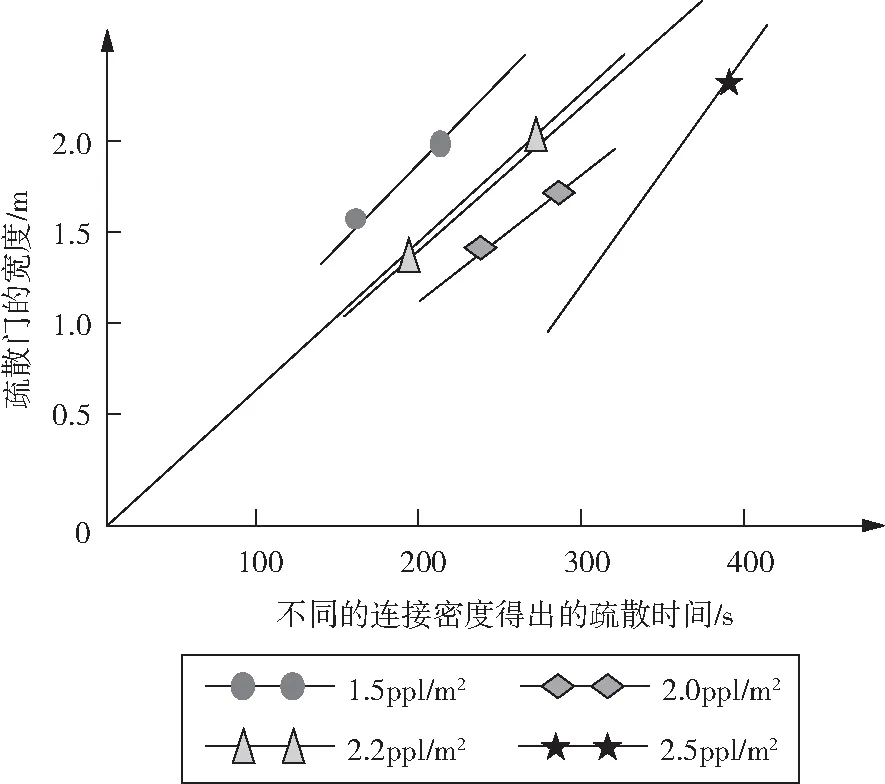
图2 不同的连接密度的疏散时间Fig.2 The evacuation time gotten by different connection density

3 实例分析

某大型超市长、宽、高分别为40、20、5m，有3个安全出口，中间安全出口宽度为3m，两边安全出口宽度为1.5m。该超市集购物、餐饮于一体，客流量较大，商品种类繁多，可燃易燃物较多，存在较大火灾危险性。超市以400人为基准，根据多次疏散演练得出平均疏散时间为210s。

3.1 Evacuation NZ疏散模型的疏散时间

紧急情况时，假设有400人从超市向外疏散，形成“过渡排队等候”现象，即疏散门口已经呈现拥堵状态。在2个疏散宽度相同的安全出口形成2簇人群，虽然节点密度没有变化，但局部连接密度增加，也就是连接密度发生变化。

设

为楼梯口排队人员数量，其单位时间内的变化率为：

(3)

式中：

—到达的人数；

—离开的人数。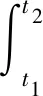

(4)

疏散时间

为：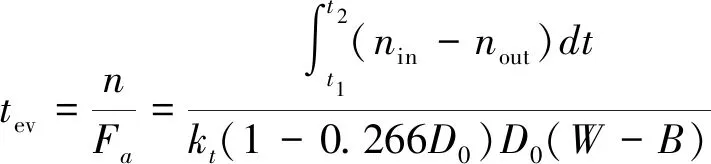

(5)

疏散时间是一个变量，它不仅是连接密度的函数，还受很多不确定因素影响。因此，实例中连接密度为2.2人/m时，计算出疏散时间为194s，即Evacuation NZ疏散模型模拟出的疏散时间为194s。

3.2 传统工程算法计算疏散时间

(1)疏散时间

预测。疏散时间即从疏散开始至到达建筑安全出口外的时间。疏散时间由步行时间

(从最远疏散点到安全出口所需的步行时间)和人员通过出口滞留时间

(计算区域人员从出口全部通过所需时间)构成，即：

(6)

步行时间：

(7)

式中：

—步行最大距离，m，取50m；

—步行速度时间，m/s，一般情况下取1m/s。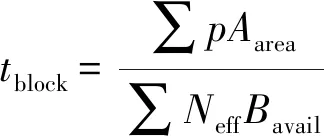

(8)

式中：

—人员密度，人/m，取0.9人/m；

—计算区域面积，m；

—出口有效流出系数，取1.1人/m·s；

—出口有效宽度，m。(2)疏散时间

。

疏散时间有步行时间和出口滞留时间组成，如下：

(9)

计算得

=131.8s

3.3 结果分析

对于同一建筑物，应用Evacuation NZ疏散模型除考虑连接密度外，还考虑疏散人员心理、社会行为等因素对疏散时间的影响。因此，Evacuation NZ疏散模型利用连接密度得出的疏散时间比采用传统工程算法得出的结果更接近实际。对于满足一定条件的建筑物可以利用Evacuation NZ疏散模型模拟疏散时间，为消防监督人员和单位估算模拟疏散时间提供参考价值。

4 结论

基于Evacuation NZ疏散模型模拟火灾中人员疏散时间，主要得出以下结论：

(1)计算机疏散模拟模型在模拟过程中可根据实际情况随时更改疏散人员行为，与传统工程算法相比，它更接近火灾人员疏散的真实情况，因此，在今后的研究过程中可通过大量模拟和实验结果对传统工程算法进行修正。

(2)在今后应用计算机模型进行火灾疏散时间的研究时要重视数据积累，同时对火灾疏散人员行为进行更深入的研究。