一种轮式移动机器人滑模轨迹跟踪控制器设计及其参数优化方法

高兴泉，丁三毛，黄东冬，刘志成，肖新宇

(吉林化工学院 信息与控制工程学院，吉林 吉林 132022)

目前，为了让轮式移动机器人完成对复杂轨迹的跟踪，常运用PID、自适应、反演等算法设计轨迹跟踪控制器[1].在种类繁多的控制方法中，建构简单、鲁棒性强的滑模变结构算法被广泛用于轮式移动机器人轨迹跟踪控制[2].一个控制性能优良的滑模控制器，可以使轮式移动机器人更加稳定、快速、精确地完成跟踪控制.在设计滑模控制器时，趋近律的选择

尤为重要，会直接影响控制器的性能，依据被控对象的特点设置适合的控制器，能够使控制效果更好[1-3].其中指数趋近律在众多趋近律中具有结构简单、趋近速度快的优点，能够在最短时间内实现收敛.本文一共设计3个指数趋近律，其中外环由两个指数趋近律设计，实现轮式机器人位置在x轴与y轴两个分量的跟踪控制，内环由一个指数趋近律设计，实现轮式移动机器人在运动时对位姿角的跟踪[3-4]，然后将所设计的控制器分别进行Lyapunov稳定证明确保每个控制器都能渐近稳定.

在对滑模控制器设计时，参数的整定也是设计的难点.一组好的参数能够大大提高跟踪的速度，也能够削弱抖振现象.起初一般是人工根据经验对参数进行试凑整定，导致在选择上出现较大的随机性，较难选出较精确的参数，跟踪品质较差[5].随着控制品质的不断增加，简单的人工随机调参已经无法满足高品质的控制需求，而计算机技术的发展给复杂的调参带来了曙光.科研人员很好的利用计算机的高速计算能力，经过多次迭代，进而寻找到一组最优的参数，使控制效果更好.在众多优化算法中，蚁群算法、遗传算法和粒子群算法等群智能算法可以解决滑模控制器参数选择这一复杂问题[6].与其他算法相比，粒子群可以寻找最优解、算法设计简单易懂等优点，在工程实验中应用比较广泛.本文在设计在完滑模控制器后，为达到更好的控制效果，利用粒子群优化算法强大的寻优功能搜寻出一组最优参数，更好更快地实现轮式移动机器人轨迹跟踪控制，粒子群算法的加入大大降低了人工调参的随机性和耗时性[5].

1 全动态误差模型的建立及问题描述

根据图1，本文所使用的轮式移动机器人模型有3个轮子，其中前面的轮子为导向轮，使轮式机器人转弯更加灵活并保持轮式移动机器人的平衡，后面两个轮子为驱动轮，为机器人的运动提高力矩及实现差速转弯.

图1 轮式移动机器人模型

假设轮式移动机器人运动过程中轮子只与地面发生滚动，可以对其运动的特点建立运动学模型为

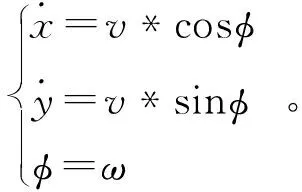
(1)

其中：x，y为运动时质心的位置坐标；φ为轮式移动机器人运动过程中轴线与x轴方向的夹角；v轮式移动机器人的瞬时速度[6].

2 滑模控制器的设计

2.1 闭环系统设计

整个闭环系统分为外环系统与内环系统，其中位置子系统为外环系统，姿态系统为内环系统，由内环与外环共同构成一个双闭环系统.图2为闭环系统框图.其中内环输入信号φd与 由外环与系统输出提供.

图2 闭环系统结构图

2.2 位置控制律设计

首先对轮式移动机器人运动时的位置设计控制律，使轮式移动机器人在x，y坐标轴方向上的运动轨迹趋近期望轨迹[6-7].

将期望轨迹定义为[xdyd]，则

(2)

其中xe=x-xd，ye=y-yd.

(3)

其中：k1,2>0，η1,2>0.

(4)

在轮式移动机器人运动时，如果φ跟踪上φd运动的轨迹，则轮式移动机器人在姿态上完成跟踪，而运动初始阶段误差的存在会影响系统稳定.

为此，需要将式(4)求得的角度φ当成理想值，即取

(5)

并设计一个比位置控制律收敛更快的姿态控制算法，使φ尽快跟踪φd.

由u1，u2可知，可以得到轮式移动机器人速度v这个控制量

(6)

2.3 姿态控制律设计

为实现角度?能跟踪上φd，对姿态控制律进行设计，设计步骤参考位置控制律设计.设计姿态的指数趋近控制律为

(7)

其中，k3>0，η3>0.

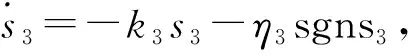
3 粒子群优化轮式移动机器人滑模控制器

由于在滑模控制器设计时，趋近律系数与切换函数的边界层厚度会严重影响轮式移动机器人轨迹跟踪的效果，而这些参数在选择时存在较大的随机性，很难选出合适的参数实现高品质的跟踪控制.为了使轮式移动机器人更快更稳地消除偏差，可以利用粒子群算法对趋近律系数与切换函数的边界层厚度进行优化[8].

粒子群算法是一种通过大量参数进行多次迭代，优化出一个最优结果的方法，可以对个体寻优，也可也进行全局寻优[6].通过种群搜索最优参数，在使目标函数J的值最小的前提下实现轮式移动机器人轨迹跟踪控制.粒子群算法流程如图3所示.

图3 粒子群算法流程图

通过前面控制器的设计，该系统有6个参数可以优化，分别是位置控制器设计时的k1，k2；姿态控制器设计时的k3，三个变量一一对应的边界层厚度η1，η2，η3等参数[9].图4为粒子群算法优化滑模参数系统框图.

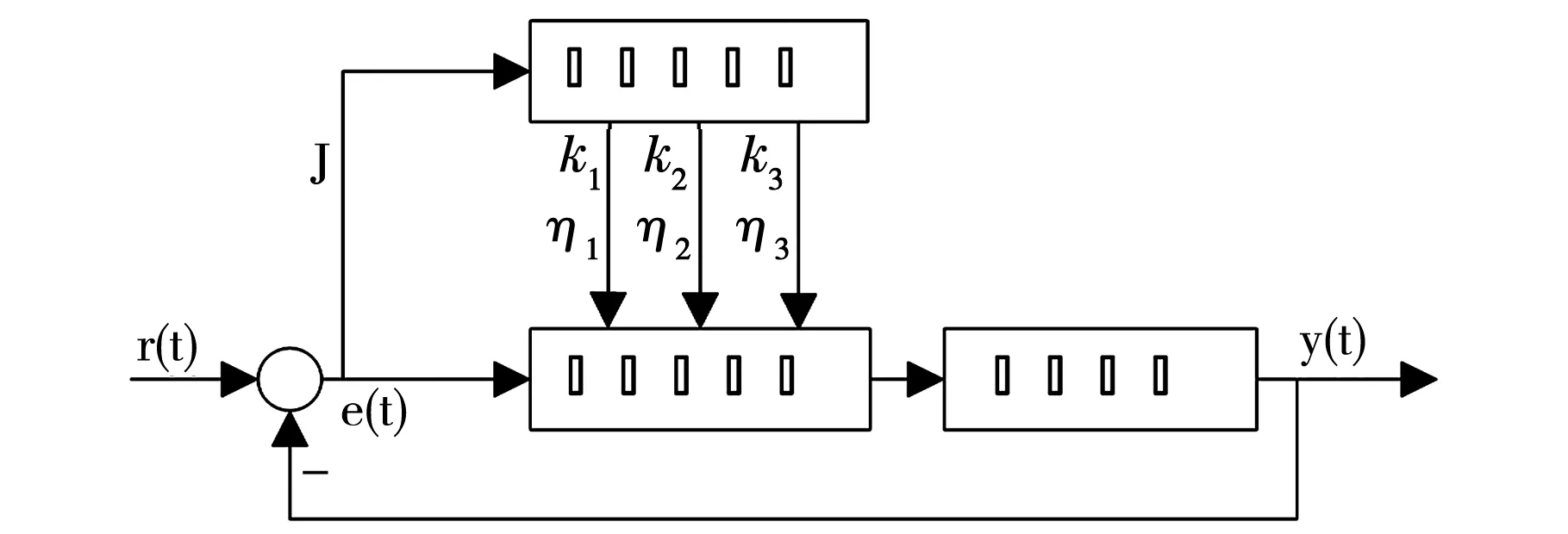
图4 粒子群算法优化滑模参数系统框图

通过建立目标函数J，以实现跟踪时各个变量的偏差积分和最小为目标，可建立各变量误差与时间轴面积之和为目标函数[9]，即：

(8)

在利用粒子群算法寻优时，对6个参数设置的范围均为0到50，随机将这个范围分成35个种群，每个种群进化30次，从中选出一组参数使目标函数J最小，改组参数即为这个范围内最优参数.由图5为粒子群优化时的适应度曲线，由图可知，适应度值逐渐降低，在大约16代时达到稳定状态.

图5 适应度曲线

通过粒子群算法的多次迭代，得到最后迭代的适应度值大约为0.115，其中k1=42.787 9，k2=46.486 2，k3=48.985 8，η1=42.712 8，η2=39.512 0，η3=25.902 9.

4 实验仿真及结果分析

实验中对曲线轨迹进行跟踪，验证设计的双闭环滑模控制器能够实现轨迹跟踪，同时进行粒子群优化得到的参数与人工经验整定参数进行对比.通过人工经验进行调整得到的参数为k1=0.3，k2=0.3，k3=3，η1=0.5，η2=0.5，η3=0.5.

以跟踪曲线轨迹为例，该轨迹可以由以下函数描述

(9)

对轮式移动机器人的初始状态进行定义x0=-5，y0=5，φ0=5.轮式移动机器人在粒子群优化参数与人工经验整定参数下的跟踪轨迹如图6所示.

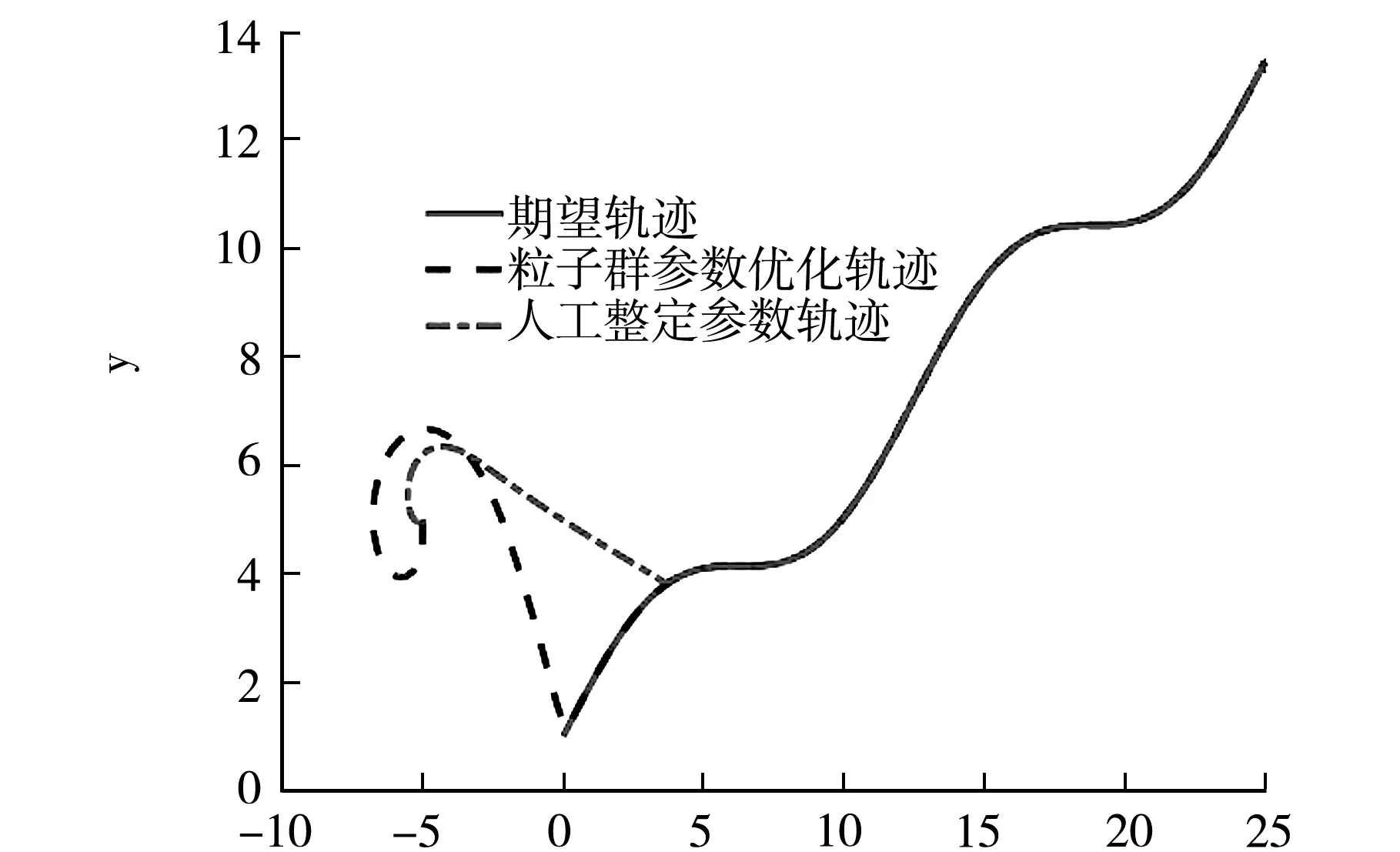
x图6 期望轨迹与轮式移动机器人运动轨迹

轮式移动机器人的初始状态与目标轨迹的初始状态不同，导致轮式移动机器人在初始时刻各状态均出现误差，为了在各状态体现出粒子群优化得到的参数在控制效果上相对人工经验整定的更好，下面选取了位置、角度的误差曲线进行对比，如图7所示.

时间/s图7 曲线轨迹各变量误差曲线

根据图7所的对比结果，采用粒子群优化得到的滑模控制器参数可以使轮式移动机器人的跟踪误差逐渐减少，即e→0，并保持稳定的运行效果，相较于人工整定的参数具有更好的控制效果.同时，利用粒子群优化算法进行优化，大大节约了人工进行调参所花的时间，明显提高了调整参数的效率[10].

5 结 论

为使轮式移动机器人实现轨迹跟踪，首先从轮式移动机器人的运动学模型着手，根据轮式移动机器人的3个状态，应用滑模变结构控制算法，分别在轮式移动机器人位置上的两个状态与姿态上的一个状态设计控制器，可以使轮式移动机器人各状态误差收敛到0.在实现轨迹跟踪后，应用粒子群算法优化所建立的目标函数J，得到目标函数最小时的最优参数.从仿真结果对比中明显看出，通过利用粒子群优化算法得到的参数在成功实现轮式移动机器人对曲线的跟踪的基础上，控制效果明显比人工整定参数的控制效果更优，大大提高了双闭环滑模控制器的控制效果.这也体现出了将粒子群优化算法应用到所设计的滑模控制器后，大大提高滑模控制器控制效率.