湍流尺度和相干参数对传输光强的影响
毛鑫峰,吴 昊,覃万富,周 鹏,顾金林
(中国卫星海上测控部,江苏 江阴 214400)
1 引 言
针对部分相干光的研究开始于20世纪七八十年代,在Wolf和Carterl提出的准单色高斯部分相干光理论的基础上不断发展[1-3]。在实际应用中,受激光器自身参数以及大气湍流等环境因素的影响,光束波前的随机性增加,相干光多数情况下以部分相干光的形式存在[2-3]。因此,深入研究部分相干光的大气传输特性具有重要的实际意义。目前针对部分相干光的研究更多的侧重于大气湍流介质中的光束发散角、闪烁效应、光强分布和空间相干度。Richlin等人运用交叉谱密度函数研究了部分相干光在大气湍流中的光强闪烁和孔径平滑因子[4-5]。Wu等人研究比较了GSM(Gaussian Schell-model)光束在真空和湍流大气中横向相干长度等传输特性,得到了“与完全相干光相比,部分相干光受大气湍流影响更小”的结论[6]。Friberg研究了部分相干光在自由空间中的光束束宽和波前曲率半径特性,并分析了空间相干特性[7]。柯熙政和季晓玲研究了部分相干光在大气湍流中的光束扩展及角扩展问题[8-9]。王华和李成强研究了高斯-谢尔模光束在大气湍流中的空间相干长度特性[10-11]。部分相干光在大气信道中的传输问题也是无线光通信领域研究的热点,并取得了一定的成果[12-15]。虽然目前针对斜程大气传输的部分相干光影响因素研究较多,但缺少湍流内外尺度和不同光源相干参数对部分相干光光强影响的研究,同时随着理论模型的不断改进和实际需求的变化,还需要对部分相干光在大气湍流中的传输特性开展进一步的分析。
本文根据广义惠更斯-菲涅尔原理,利用交叉谱密度函数推导得到了斜程大气传输过程中的光强表达式,根据表达式分析了湍流内外尺度和不同光源参数对接收光强的影响,并进行了理论分析。
2 斜程大气传输的光强分布及相干特性理论分析
在发射平面处,发射光束高斯光场的振幅可表示为[16]:
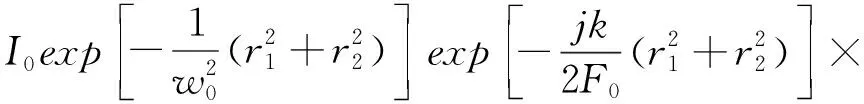
(1)
其中,r1和r2表示垂直于发射方向的平面内横向位移矢量,w0表示发射光束束腰半径,σ0表示光源部分相干长度,F0表示波前曲率半径,k表示光波数。
根据惠更斯-菲涅尔衍射原理,GSM部分相干光束经过大气湍流远距离传输后的目标处的交叉谱密度函数可表示为[16-17]:
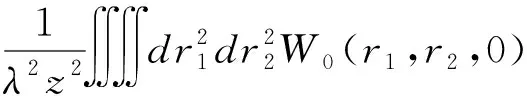
〈exp[φ(r1,ρ1)+φ*(r2,ρ2)]〉×
(2)
ρ1和ρ2表示目标平面内的横向位移矢量,其中W0(r1,r2,0)表示发射光的交叉谱密度函数。
(3)
球面波复相位的互相关函数可表示为[14]:
〈exp[φ(ρ1,r1)+φ*(ρ2,r2)]〉
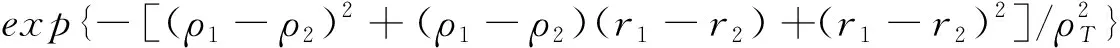
(4)
(5)
(6)
其中,κ0=2π/L0;κm=5.92/l0;l0表示湍流内尺度;L0表示湍流外尺度;θ表示斜程传输时的天顶角。斜程大气湍流传输的大气结构常数是随高度变化的分布函数,斜程大气湍流传输应用较多的是Hufnagel-Valley湍流模型[15]:
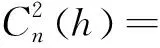
(7)
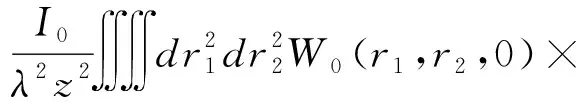
exp{-[(ρ1-ρ2)2+(ρ1-ρ2)×
(8)
利用质心坐标和差分坐标变换[17]:
(9)
(10)
通过积分运算,可以近似得到传输距离z处的交叉功率谱密度函数:
(11)
(12)
(13)
(14)
(15)
(16)
(17)
3 数值分析
根据理论分析得到的公式(17),斜程大气传输过程中光强分布主要受光源参数、湍流尺度和天顶角的影响。针对以上影响因素本文开展数值模拟分析,并给出理论解释,数值仿真中的参数设置如表1所示。

表1 数值模拟中的参数
分析不同湍流尺度和光源相干参数对光强分布的影响,仿真过程中首先对接收平面处的接收光强进行归一化处理,z=5 km,天顶角θ=0°,湍流外尺度L0=3 m,内尺度为l0=1 cm,1.5 cm,3 cm,5 cm,相干参数分别取ζs=1,3,5,10时,接收平面处归一化光强分布如图1所示。由结果可得,在相干参数一定的条件下,湍流内尺度越大接收平面上的光斑尺寸越大,归一化光强越小。部分相干光的归一化光强小于完全相干光,但相干参数越大归一化光强受湍流内尺度大小变化的影响越小。其他参数保持不变,湍流内尺度l0=1 cm,湍流外尺度分别取L0=3、5、7和10 m时,归一化光强分布如图2所示,随着湍流外尺度的增加,归一化光强下降,接收平面上的光斑展宽很小。通过比较图1和图2,在相同相干参数条件下,归一化光强受湍流内尺度的影响较大,光束展宽作用明显。以上结果说明在斜程大气传输过程中光强分布主要受湍流内尺度的影响。理论分析,斜程大气传输过程中,由于湍流外尺度远大于光束的光斑半径,对于小尺寸光束来说湍流外尺度是相对均匀稳定的介质,因此光束半径和接收光强受湍流外尺度的影响较小。而湍流内尺度较小,单位面积内湍流内尺度的变化较大,因此湍流内尺度对归一化光强衰减和光斑展宽作用较大。
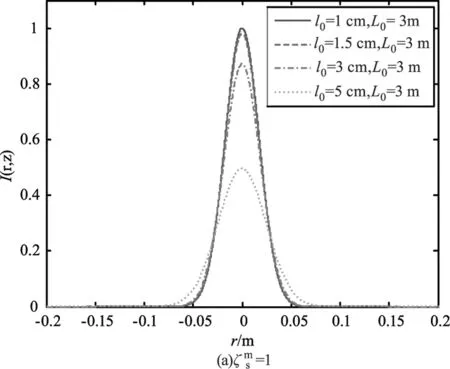
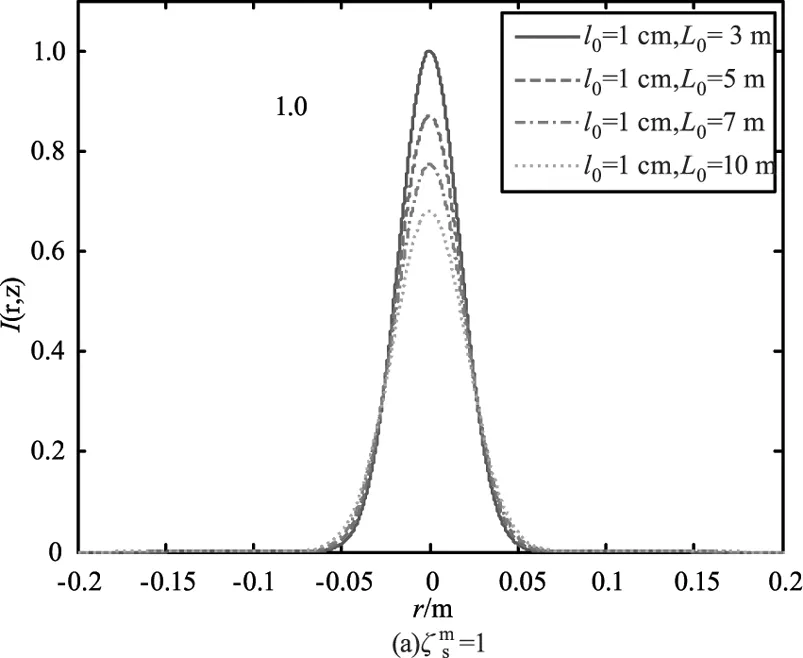
图3和图4分别表示不同湍流内尺度和不同湍流外尺度的归一化光强随传输距离的变化曲线。由结果可以看出,当传输距离小于4 km时湍流内外尺度对归一化光强的影响很小,可以忽略不计。当传输距离大于4 km时,湍流尺度的变化对归一化光强的影响表现更突出。光源相干参数越大,随传输距离的增加归一化光强值下降速度越快,归一化光强受湍流尺度变化的影响越小。
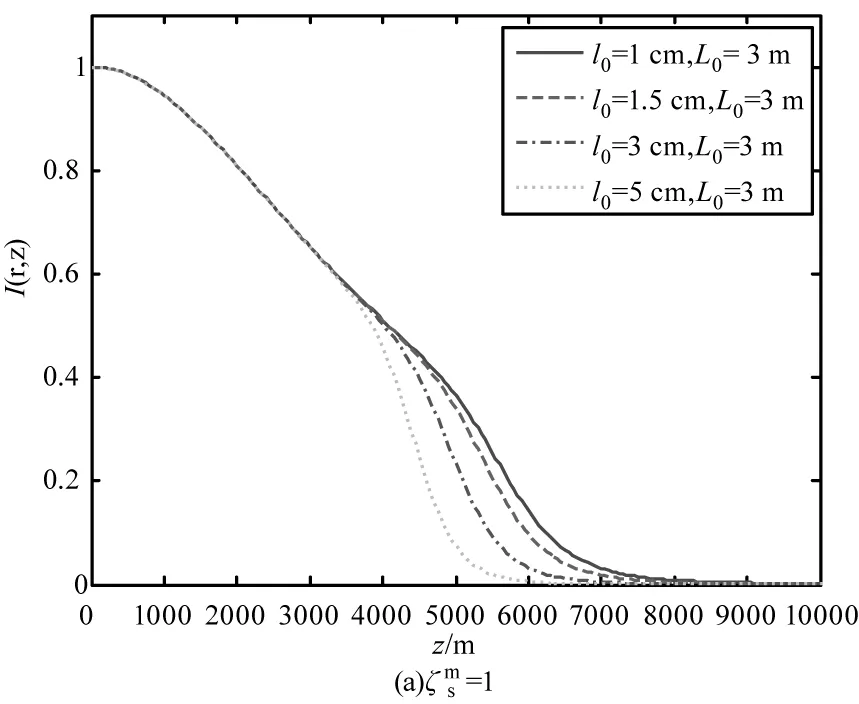
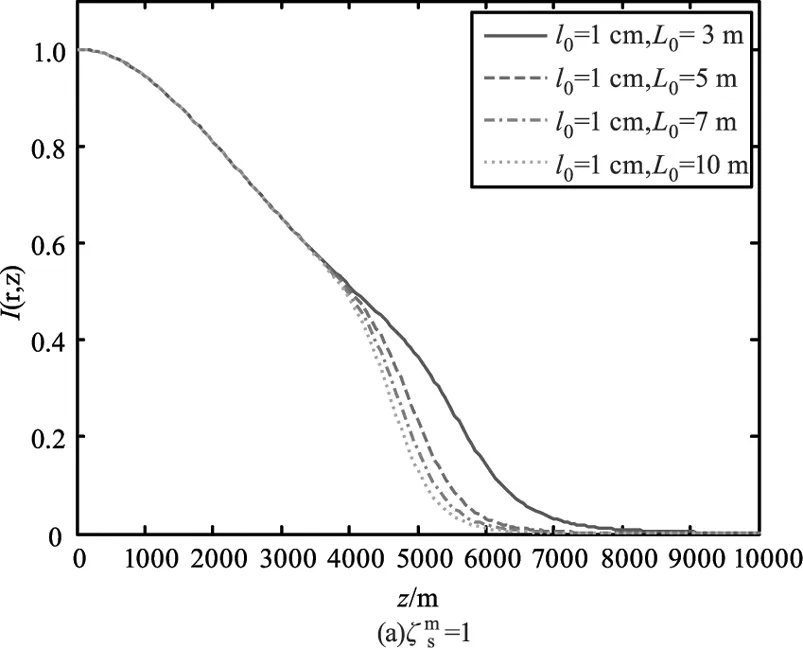
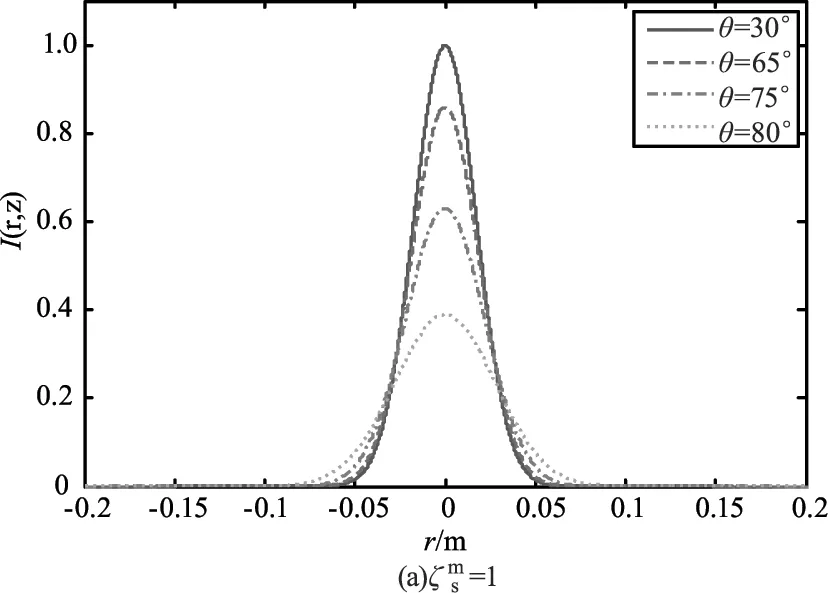
图5表示湍流内外尺度一定时,不同天顶角在不同光源相干参数下的归一化光强分布。由结果可得,随着天顶角的增大,接收平面上的光斑尺寸越大,由于光束的扩展导致归一化中心光强下降。在小天顶角时,归一化光强受光源相干参数的影响较大;在大天顶角时,归一化光强受光源相干参数变化的影响较小。理论分析,在传输距离一定的条件下,随着天顶角的增加传输过程中的斜程大气湍流的影响加大,使得光束展宽同时接受平面上的平均光强下降。当天定角较小时归一化光强主要受光源相干参数的影响,随着天顶角的增加,大气湍流的叠加效应增加,归一化光强受天顶角变化较小,此时湍流尺度的影响占主导地位。
4 结 论
本文结合广义惠更斯-菲涅尔原理,以部分相干光为例推导得到了斜程大气传输的光强表达式,根据该表达式分析了湍流大气的内外尺度、光源相干参数和天顶角对接收光强的影响,并进行了数值模拟分析。结果表明:斜程大气传输过程中,湍流内尺度对接收光强的影响比湍流外尺度的影响大。光源参数越大,接收光强受湍流内外尺度变化的影响越小。且在传输距离小于4 km时,湍流内外尺度变化对接收光强的影响可以忽略不计。相干参数对小天顶角时的光强影响较大,随着天顶角的的增大,大气湍流对接收光强的叠加影响占主导作用。本文的分析对光束在斜程大气中的传输具有实际意义。

