基于分支限界算法的横折臂混凝土布料机构避障布料分析

王小安 李佳伟 黄跃申

1. 上海建工集团股份有限公司 上海 200080；

2. 上海高大结构建造工艺与装备工程技术研究中心 上海 201114

混凝土布料机是用于进行混凝土出料导向的关键设备。在超高层建筑建造过程中布料机构的合理选择对保证工期与质量尤为重要。随着超高层建筑工程施工现场工业化建造方式的不断发展，混凝土布料机呈现出新的发展趋势和要求，其与整体钢平台模架等大型装备逐渐要求实现一体化，其施工操作也逐渐要求实现智能化[1-3]。

超高层建筑施工过程中，结构顶部通常布置有大型塔机、施工升降机等高出结构施工面的机械设备，对同样布置在结构顶部的混凝土布料机构而言，为实现高效连续的混凝土浇筑，其需要具备绕过大型塔机等障碍物实现背面区域混凝土布料施工的能力。目前常用的竖折臂布料机虽然布料能力强，但避让障碍物的能力较差，现场常常存在浇筑死角区域。针对上述问题，有关研究人员提出一种横折臂混凝土布料机构[4]，它主要由一个可全回转的基座、水平臂架和连接臂架的关节组成，连接臂架的关节平置、转轴竖直，臂架在水平面内转动。目前混凝土布料机构的智能化控制技术研究多集中在传统的竖折臂布料机上[1,5-6]，针对横折臂布料机构的研究基本空白。为确保横折臂布料机具有有效的避障能力，有必要将其置于具有大型塔机等障碍物的超高层结构顶部实际环境中，进行浇筑全覆盖能力分析。

分支限界法是按照广度优先的方式对解空间（状态空间）进行搜索求得最优解，对有约束条件的优化问题的求解尤为高效[7-10]。因此，在横折臂布料机构躲避障碍物可行性分析中可应用该方法。

本文针对横折臂混凝土布料机构，对其躲避障碍的可行性进行理论分析，并基于分支限界法设计高效可行的求解算法，为横折臂混凝土布料机构智能化控制技术研究提供了理论基础。

1 横折臂混凝土布料机构的简化模型

解决横折臂混凝土布料机构避障布料问题的关键在于横折臂混凝土布料机构臂架和障碍区域的相对位置关系分析，因此应首先建立包含表征横折臂布料机构、结构布料区域和障碍区域的位置函数的数学模型。

1.1 横折臂布料机构状态函数

1.1.1 三折臂布料机构的状态函数

为描述横折臂布料机构的空间布料位置，需建立一个统一坐标系。由于横折臂各臂节在同一平面内相对转动，同时考虑到建筑结构布料区域和障碍区域用平面位置描述不影响问题的求解，因此建立一个以横折臂布料机构的中心（起点）为坐标原点O的平面坐标系，坐标系的x、y轴可参考建筑结构轴线和障碍区域的位置，以简化模型的原则确定，如图1所示。

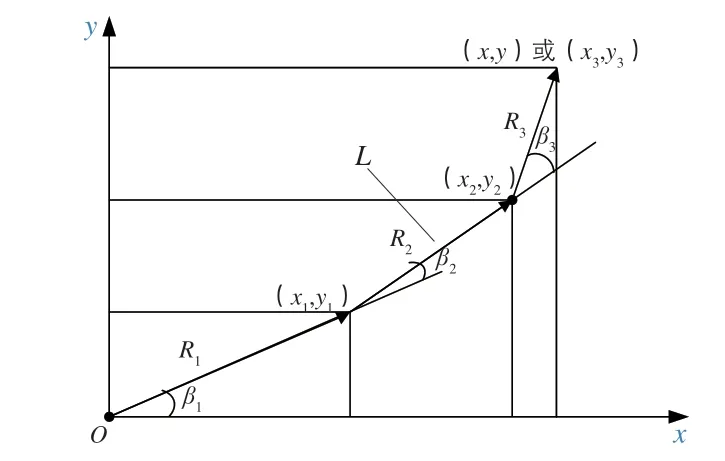
图1 横折臂布料机构数学模型

在该坐标系中可以唯一确定3节横折臂布料机构各臂节的位置状态的一组函数称为该横折臂布料机构的状态函数。横折臂布料机构有3个臂节，每个臂节所在位置可简化为有向直线段，故横折臂布料机构的状态函数FL可用一组3条有向线段表示，记为L，如图1所示。由于各线段是直线，线段的起点为坐标原点，则横折臂布料机构的3条线段的终点坐标分别为：{(x1,y1),(x2,y2),(x3,y3)}，则线段组L上的点可用式（1）表示：

式中，i＝1时，出现的(x0,y0)为线段L的起点，即原点(0,0)。由于xi－1、xi的相对大小关系不定，为便于推导计算，规定线段Li的定义域x∈[ximin,ximax]，ximin＝min{xi－1,xi}、ximax＝max{xi－1,xi}。线段定义域在y坐标轴上的，可作相应规定和推导，下同。定义域所在坐标轴的不同对问题的分析推导没有本质影响，故下文推导默认各线段的定义域在x坐标轴上。

显然，通过式（1）的描述，线段组L与这3条线段的终点坐标组成的一组有序点列{(x1,y1),(x2,y2),(x3,y3)}唯一对应，则3节横折臂布料机构的状态可用这组空间点列表示，即式（2）：

L:{(x1,y1),(x2,y2),(x3,y3)} （2）

另一方面，有向线段可用向量表示，向量的起、终点分别为臂节的近端、远端，方向为臂节的近端指向远端，单独考察每个臂节的向量，可表示为式（3）：

由于现场施工控制中，横折臂布料机构的臂节方位角无法精准辨别，而相对于方位角，臂节之间的角度或转动关节的转角直观可测，便于直接应用，故横折臂布料机构的状态函数以臂节相对转角的表示形式FL(β1,β2,β3;R1,R2,R3)有更大的参考作用，有利于横折臂布料机构的数字化控制。

1.1.2 结构布料区域位置函数

建筑结构布料区域是指建筑施工过程中需要混凝土浇筑的墙、柱等位置，一般来说结构的布置多为直线段。因此在上述坐标系中，可以用同样的线段表达方式确定建筑结构布料区域的位置。若建筑结构布料区域由N条线段组成，则建筑结构布料区域位置函数FS(x,y)为式（8）：

1.1.3 障碍区域位置函数

建筑结构施工现场一般有塔机和施工升降机等机械设备，施工升降机最高点通常高出作业面（平台）3～4 m，可适当提高横折臂布料机构的高度，以越过施工升降机的高点，而塔机的高差较大，难以采取经济有效的方法克服，布料机构工作时的障碍一般有施工用的塔吊。

一般地，假设存在某一障碍区域S，该区域S边界Lobs可通过M条线段无限逼近，且M条线段是封闭的，则边界Lobs可以用M条线段表示。同样的，由于各线段是直线，边界Lobs与这V条线段的终点坐标组成的一组有序点列{(x1,y1), ,(xj,yj), ,(xM,yM)}唯一对应。

由于区域S边界封闭，第1条线段的起点应是第M条线段的终点，为便于表示和推导分析，在上述有序点列{(x1,y1), ,(xj,yj), ,(xM,yM)}前增加一个点(x0,y0)，并令(x0,y0)＝(xM,yM)，即障碍区域的边界表示为一组有序点列〔式（9）〕：

1.2 横折臂混凝土布料机构避障分析

横折臂混凝土布料机构能够避开障碍区域，几何上分析即线段组L与障碍区域S无公共点，其充要条件是线段组L与边界Lobs各组成线段无公共点，当且仅当边界Lobs中的所有线段与线段组Li(x)（i＝1,2,3）均无公共点时，认为横折臂混凝土布料机构可以避开障碍区域。一般地，先分析线段组Li(x)（i＝1,2,3）与边界Lobs中任意线段Lobsj的几何位置情况，然后分析边界Lobs中所有线段的几何位置情况。

1.2.1 避开障碍线段

3节横折臂布料机构可以避开该障碍线段Lobsj，则线段组L中的每条Li与障碍线段Lobsj不相交，即方程（11）均无解。

方程无解的情况很多，没有一个可执行的通用公式计算，求解难度较大。通过考察线段组Li(x)（i＝1,2,3）和障碍线段Lobsj定义域的关系，可将方程无解的情况总体分为2种：

1）线段组Li(x)（i＝1,2,3）和障碍线段Lobsj无重合的定义域，则方程必然无解。

2）线段组Li(x)（i＝1,2,3）和障碍线段Lobsj有重合的定义域，这种情况下只需验证定义域重合的线段不相交即可。

这种验证式的求解方法较为简单，求解也容易，可大大降低求解难度，提高求解效率。

1.2.2 定义域重合关系判别

针对障碍线段Lobsj对每个线段Li(x)（i＝1,2,3）进行定义域关系分析。由于障碍线段Lobsj定义在x∈[xobsjmin,xobsjmax]上，因此仅需考察每个线段Li(x)（i＝1,2,3）的定义域与[xobsjmin,xobsjmax]的关系即可。记线段Li(x)（i＝1,2,3）中定义域与[xobsjmin,xobsjmax]有交集的线段组成的集合为{L*ij}( {Li(x),i＝1,2,3})，满足该条件的线段{L*ij}要求其定义域[ximin,ximax]中至少有一点落在区间[xobsjmin,xobsjmax]内，记该点为x*。根据定义域的定义，可得到式（12）和式（13）：

实际上，式（14）是2个线段定义域重合的判别条件。针对任意的障碍线段Lobsj，通过该式均可以找出所有线段组Li(x)（i＝1,2,3）中与线段Lobsj有重合定义域的线段。而当Li(x)（i＝1,2,3）中不存在满足式（14）的线段时，则没有重合定义域，方程式（11）无解。

1.2.3 重合定义域下避障条件

综上，可以得出横折臂混凝土布料机构避开障碍区域的充要条件如下：

在障碍区域的边界Lobs中，针对任意的障碍线段Lobsj，横折臂布料机构的状态函数FL所对应的线段组Li(x)（i＝1,2,3）不满足式（14）或在满足式（14）的条件下同时满足式（15）。

1.3 横折臂布料机构布料范围

布料范围是混凝土布料机构的重要工作性能参数，一般与布料机构各臂节长度和臂节间转角范围有关。这里将各臂节间关节视为全回转关节，即其转角范围为（－π,π）。根据向量的模的运算，易得横折臂布料机构布料距离的上限和下限，得出混凝土布料机构的布料范围如式（16）所示：

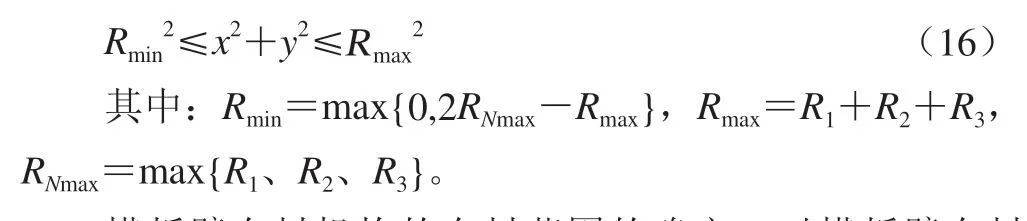
横折臂布料机构的布料范围的确定，对横折臂布料机构的设计有重要意义，在之后的求解过程中作为约束条件，也有划分解空间的重要作用。结构布料施工时，横折臂混凝土布料机构臂节长度参数已知，其布料范围可以通过式（16）进一步确定，因此在避障布料问题求解时可以作为已知约束条件加以使用。

1.4 最佳布料状态

布料机构在布料作业时的终端在建筑结构布料区域位置函数上，由于3节横折臂布料机构的关节是全回转的，所以一般情况下，3节横折臂布料机构仍有一个自由度，(β1,β2,β3)有无穷多种组合，即横折臂布料机构的状态函数有无穷多解。引入一个评价函数记为V(x,y)，衡量在相应位置布料时的横折臂布料机构的状态优劣程度，其最佳状态下的解即是最优解。

结合工程实际，当横折臂关节所受的弯矩越大时，横折臂布料机构的整体安全稳定性越差，在横折臂臂节长度和质量分布确定的情况下，关节所受的弯矩与关节的转角大小正相关。横折臂布料机构避障布料的评价函数可按式（17）选取：

由表达式可知，该评价函数的值域为（0,1]，其工程意义在于评价函数的值越大表示横折臂布料机构关节的转角越小，机械关节损害越小，整体受力上也更为安全可靠。

2 基于分支限界法的避障布料求解分析

2.1 分支限界法

结合工程实际，模型中的求解目标是验证横折臂布料机构在避开障碍的条件下对所有建筑结构布料的能力基础上，找到每个位置的最佳布料状态，式（18）则是最佳布料状态的衡量指标。

分支限界法的基本思想是对有约束条件的优化问题的所有可行解空间进行搜索。在横折臂布料机构避障布料问题中，其解是针对所有建筑结构区域的任意位置找到一组可避开已知障碍区域的最优布料状态。

基于上述分析结果，横折臂布料机构布料范围、障碍区域关键影响范围、横折臂布料机构臂节角度等约束条件都可构成可行解空间的分割条件。因此相较于穷举法等传统算法，在本工程中应用分支限界法求解具有明显的优势。

2.2 算法求解步骤分析

针对横折臂布料机构避障布料问题，应用分支限界法的求解流程如图2所示。结合本工程所具有的约束条件，生成的分支限界算法求解步骤如下：

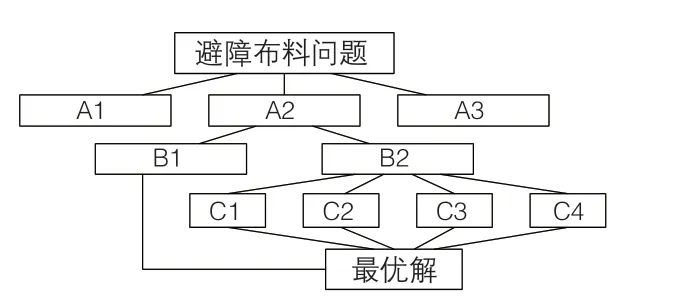
图2 算法求解流程

1）初始化数学模型，对横折臂布料机构状态函数、障碍区域函数、结构布料区域函数进行赋值。

① 以横折臂布料机构的中心（起点）为坐标原点，建立全局平面直角坐标系，将工程实际各臂节长度值赋值给算法程序中的相应参数，初始化横折臂布料机构状态函数FL(β1,β2,β3;R1,R2,R3)。

② 在全局平面直角坐标系下，输入障碍区域边界的角点坐标，初始化障碍区域位置函数Lobs(x,y)。

③ 在全局平面直角坐标系下，输入结构布料区域各线段端点坐标，初始化结构布料区域位置函数FS(x,y)。

2）根据横折臂布料机构布料范围条件划分可行解空间。根据式（16）可知，通过横折臂布料机构各臂节长度即可确定该横折臂布料机构可布料的范围，因此可将解空间分割为3个子空间，分别为A1、A2、A3，如图3所示。显然，子空间A1、A3中无法找到满足状态函数FL(β1,β2,β3;R1,R2,R3)的解，说明这种情况横折臂布料机构在该区域没有布料能力，子空间A1、A3的评价函数值为0。

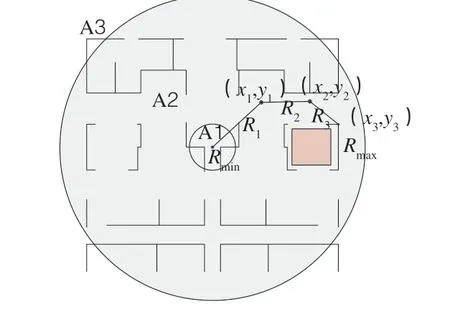
图3 布料机构布料范围划分的解空间

3）根据障碍区域关键影响范围条件划分可行解空间。如果相邻臂节不共线，臂节之间存在一定夹角，则在臂节关节处会产生一定弯矩和偏心应力，不利于机构的安全和稳定性，因此横折臂布料机构最佳的布料状态是所有臂节共线。将横折臂布料机构中心点视为光源，如图4所示，根据障碍区域是否遮挡光线，将解空间划分为B1、B2子空间。对于没有被障碍区域遮挡的子空间B1，其中的布料位置可与横折臂布料机构中心点通视，状态函数FL(β1,β2,β3;R1,R2,R3)的求解十分容易，可直接应用评价函数求解子空间的最优解。对于障碍区域遮挡的阴影部分，横折臂布料机构不能直线到达这部分区域位置上布料，这加大了横折臂布料机构布料难度，子空间B2的评价函数因障碍区域的影响难以直接确定，继续划分解空间求解。

图4 障碍区域关键影响范围划分的解空间

4）根据横折臂布料机构臂节角度条件分解可行解空间。针对上述子空间B2区域内的某一布料位置，如图5所示，寻找横折臂布料机构可避开障碍的状态函数的最优解。臂节的关节可全回转，故每个臂节角度范围为（－π,π]。但当布料位置确定后，各臂节的长度一定，决定了臂节间关节角度处在一个有限范围内。因此可以将解空间继续分割优化求解。根据三角形的三边关系定理，第一节臂节的终点到布料位置的距离有上下限，因此横折臂布料机构第一臂节角度β1（方位角α1）限定在一个范围。结合子空间B2区域，根据角度β1的范围将解空间划分为4个子空间，分别为C1、C2、C3、C4，如图5所示。

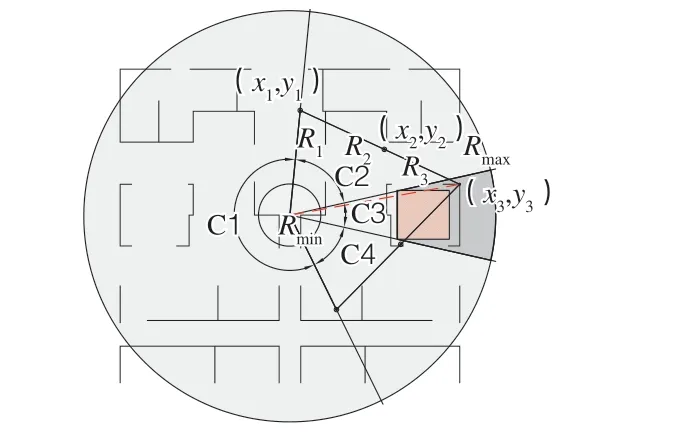
图5 布料机构臂节角度划分的解空间

5）对分支可行解空间分别求解，并对解进行评价验证。该层级下各子解空间为末枝子空间，应用评价函数V对各个解进行评估，最终得出最优解。

3 工程算例分析

3.1 工程概况

某超高层建筑采用钢筋混凝土核心筒-钢框架结构，其核心筒结构典型平面图如图6所示。核心筒结构施工采用整体爬升钢平台模架技术，施工用塔机采用内置爬升式M900D型塔机，安装位置如图中所示。拟采用3节横折臂布料机构进行核心筒结构的混凝土浇筑施工，臂节长度参数依次为11、8、6 m，横折臂布料机构的基座安装在整体钢平台上。

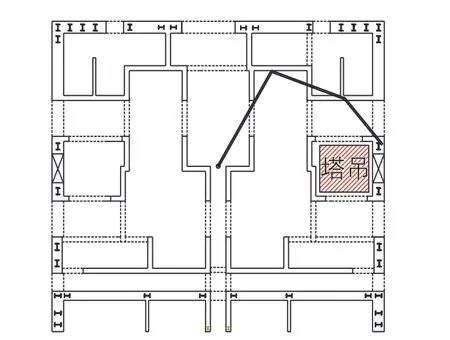
图6 某超高层建筑核心筒结构典型平面

3.2 计算模型

将上述求解算法采用Matlab软件进行参数化编程。以横折臂混凝土布料机构的基座点为原点建立恰当的平面直角坐标系，提取结构布料区域和障碍区域的坐标，将坐标和臂节长度的参数输入Matlab程序进行计算。

3.3 结果分析

通过Matlab程序计算，得到了横折臂混凝土布料机构避障布料的结果。结果显示，该臂节长度组合的布料机构可满足该建筑核心筒结构的混凝土布料，并且具备避让障碍的能力。选取部分具有代表性的布料位置（P1ü P10）的最优解求解结果，其横折臂混凝土布料机构的最佳布料状态如图7、图8所示。从图中可以看出对于P1ü P10等布料位置，横折臂混凝土布料机构均可满足布料要求，而图中P4、P5、P6在障碍区域的影响范围内，其最佳布料状态则显示布料机构的臂节分别需向障碍区域的上方、下方转动。

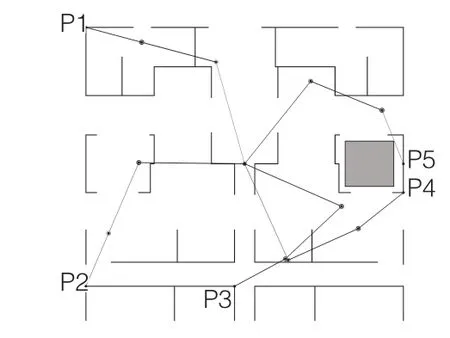
图7 P1—P5布料位置的最佳布料状态求解结果

结构布料位置（P1ü P10）的评价函数值如图9所示。图中可以看出不同布料位置的最佳布料状态不同，各布料位置的评价函数值均在0.6以上。

图9 P1—P10布料位置的评价函数值

通过算例分析结果可以看出，基于分支限界法设计的横折臂混凝土布料机构避障布料最佳状态的求解算法高效可行，对于结构混凝土布料施工具有一定的指导意义。

4 结语

本文基于分支限界算法，对横折臂布料机的避障可行性进行了分析，主要得到如下结论：

1）通过对横折臂混凝土布料机构、建筑结构布料区域、障碍区域的合理简化，在平面坐标系下建立了横折臂混凝土布料机构避障布料的数学模型，推导了横折臂布料机构考虑关节转角的状态函数。

2）通过对横折臂布料机构状态函数和障碍区域边界函数的位置关系分析，在线段定义域重合的判别条件的基础上，推导了横折臂混凝土布料机构避开障碍区域的充要条件。

3）结合模型的约束条件，基于分支限界算法，进行了横折臂布料机构避障布料问题的求解算法设计，并通过工程算例验证了算法的高效可行。