新常态下小学数学课堂创新思维训练
福建省南平市建阳区实验小学 施贵旺
创新思维是指发明或发现某种新东西的思维过程,它的显著特点是能够提供新颖独创的、有价值的思维成果,常见的有:联想思维,求异思维,求同思维,直觉思维,违反常规思维等。那么,如何在小学数学课堂中培养学生的创新思维呢?笔者结合教学实践,谈几点体会。
一、质疑问难,培养学生联想思维,在实践中创新
“学贵有疑”,学生先通过自学发现问题,提出问题,解决问题,教师再辅以创设情境,激发学生质疑问难的兴趣,变被动学习为主动学习,在探索中迸发创新的火花。例如,教学《圆柱的侧面积计算》时,笔者先让学生观察圆柱的侧面,让学生思考圆柱的侧面积应如何计算。学生各抒己见,有的学生说:“侧面是一个曲面,我们不能计算它的面积。”也有的学生提出:“虽然我们没有学过如何计算一个曲面的面积,但是,能不能把它转化为我们学过的图形来计算呢?”笔者充分肯定了这位学生的想法,并让学生动手操作,把圆柱的侧面展开,很多学生都沿着圆柱的高剪开侧面,展开为长方形;也有的学生斜着剪开侧面,展开为平行四边形。虽然两个图形的形状不同,但面积都是一样的,都等于底面周长乘以高,即都顺利得到侧面积的计算方法。这样教师通过让学生主动质疑,鼓励学生创新,在实践操作过程中实现了学生个体的全面发展。
二、创设条件,挖掘思维潜能,培养求异思维
荷兰建构主义理论著名学者弗赖登塔尔说:“学习数学的唯一正确方法是实行再创造,也就是由学生本人把要学的东西自己去发现并创造出来,教师的任务是创造条件,引导和帮助学生进行这种再创造的工作,而不是把现在的知识灌输给学生。”因而在数学课教学中,笔者重视一题多解的练习,充分挖掘学生的思维潜能,培养学生的思维创新能力。
三、优化组合,依据逻辑推理,训练求同思维
求同思维是以逻辑思维为基础,强调事物间的相互联系,并通过对已有信息的理解和运用,去寻求惟一正确的结果。求同思维的目标是将问题进行科学的简化和做出正确的选择。例如,计算分数、小数混合运算时,我们常常设想将小数转化成分数,或者将分数转化成小数,或者将其中一部分互相转化后进行计算。当然,能运用运算定律简算的还要简便计算。要从这些不同的算法中确定能正确、合理、迅速计算的设想,就要对上面的各种可能进行比较和逻辑推理,做出决断,这就是求同思维。然而,当思维者知识经验丰富并具有一定的洞察力和理解力时,又会出现不依据确切的逻辑思维,而凭个人的直观知觉就对事物和现象做出某种判断,得出简洁的思维方法。每当这时,思维的“常式”被打破,思维的过程被压缩、简化,思维变迁迅速,往往透过表面现象直接涉及事物的本质,产生出乎意料的结果。
例如,一个三角形的底是2.4 厘米,高是1.2 厘米,求它的面积是多少?列式计算:2.4×1.2÷2。按照常规程序从左往右算,费时多,还不一定能求出准确值。有的学生在计算时打破常规,整体考虑,洞察出可以运用乘除互逆转换的方法,将2.4×1.2÷2转化成2.4×(1.2÷2)来算,结果直接报出了得数1.44 平方厘米。这种思维变迁产生的新颖解法,不但使问题迎刃而解,也蕴涵着思维的创新成分。
四、另辟蹊径,打破思维定势,培养直觉思维
直觉是对事物本质的一种极为敏锐的深入洞察,是对问题答案的“一眼望穿”,这是创新思维不可缺少的有机组成部分。在解题过程中,教师可以打破思维定势,另辟蹊径,激发学生的“直觉”,使问题的本质直接接通问题的结论和条件之间的通道,使问题获得别开生面的巧妙解答,加强培养学生的直觉思维。例如,笔者在教学《圆的面积计算练习课》时,出示下题:(如图1),已知正方形的面积是10 平方厘米,求圆的面积。
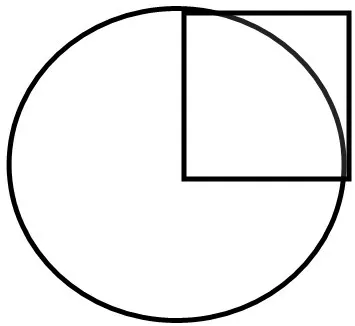
图1
按常规思维,要求圆的面积就要先求出圆的半径,对于小学生来说显然此路不通。如果我们打破思维定势,引导学生借助这题正方形面积与圆面积的特殊关系,就可以使学生找出问题的本质并获得直觉简捷的解法:因为这题正方形的面积= r ×r = r2= 10,而圆的面积= πr2,不难看出圆面积是正方形面积的π 倍,所以圆的面积是:10×3.14=31.04(平方厘米)。
五、探索规律,培养违反常规思维
长期以来,我们按传统的教学模式给学生讲解,把“标准的解题法”教给学生,结果使大多数学生过早地形成了机械的心理定势,造成思维僵化,观察事物的眼光单一。因此,教师要想重新开放学生的想象力,就必须打破种种感知。
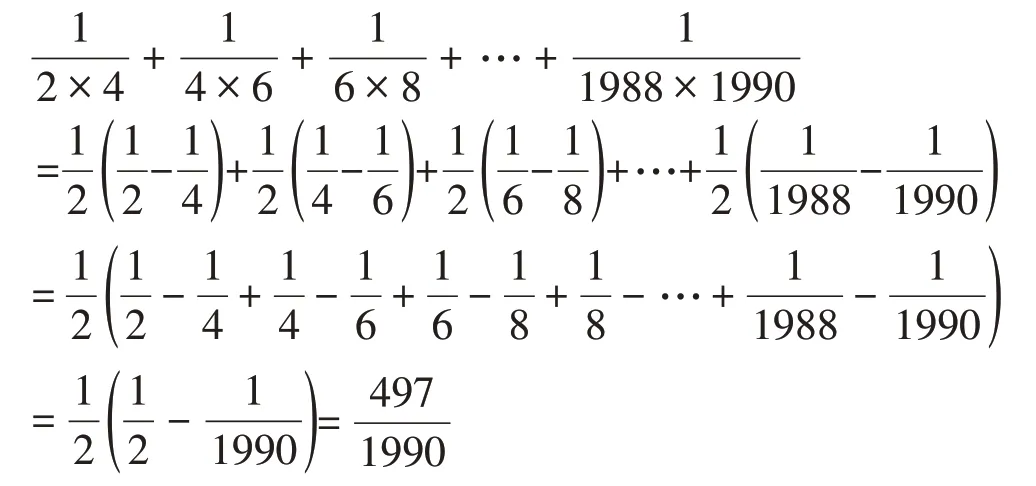
这样通过探索规律,使学生掌握了“拆项相消法”的计算技巧,所以使计算大大地简便了,有利于激发学生的学习兴趣和探索的热情,并培养了他们用违反常规的计算方法去思维的实践能力。
此外,建立民主平等、尊师爱生、教学相长、和谐相融、共享共创的新型师生关系,营造民主、和谐的课堂教学氛围,对培养学生的创新思维有巨大的促进作用。著名教育家陶行知先生说:“创造力最能发挥的条件是民主……只有民主才能解放大多数人的创造力,并且使大多数人之创造力发挥到最高峰。”可见,营造民主和谐的课堂教学氛围,能最大限度地挖掘各种类型学生的创造潜能,从而培养学生创新精神和实践能力。
总之,教学中,教师只有不断地启发、培养和发展学生的创新思维和实践能力,才能培养出符合时代要求的创新型人才。

