考虑限制性卖空的多期模糊投资组合优化模型

陈思豆，黄卓铨，杨兴雨

（广东工业大学 管理学院，广东 广州 510520）

投资组合选择是指在可供选择的多种资产上科学地分配财富，从而达到最大化收益、最小化风险等目的。Markowitz[1]提出了均值−方差(Mean-variance,MV)模型，为现代投资组合理论奠定了基础。该模型假设资产的收益为随机变量，分别用均值和方差度量资产组合的收益和风险。随后，许多学者在MV模型的基础上进行了广泛的推广[2-4]。

传统的投资组合模型大多基于随机环境，利用随机变量来刻画资产价格的不确定性。然而，在现实金融市场中投资组合决策往往受到许多非概率因素的影响，如专家意见、投资者情绪等，这些因素在很大程度上表现为模糊不确定性。自Zadeh[5]提出了模糊集合理论后，许多学者借助该理论研究不确定环境下的投资组合问题，并取得了丰富的研究成果[6-9]。上述文献均采用可能性测度刻画金融市场的模糊不确定性，但是可能性测度存在一定的局限性，即它不满足自对偶性。为改善这一缺陷，Liu等[10]提出了一个具有自对偶性的模糊测度，即可信性测度。Kamdem等[11]定义了模糊变量的可信性矩和半矩，提出了一个均值−方差−偏度−半峰度模糊投资组合模型。王灿杰等[12]建立了带融资约束的可信性均值−熵−偏度投资组合模型。Zhang[13]考虑交易费用对投资组合的影响，提出了具有不同交易费用的均值−方差随机可信性投资组合模型。

卖空交易对证券市场稳定以及价格发现都具有积极的作用。刘明明等[14]考虑了允许卖空的情形，在存在摩擦的金融市场中构建了一个均值−绝对离差投资组合模型。张鹏等[15]假定卖空所得资金与自有资本的比例为定值且资产交易量具有上界限制，提出了限制性卖空情况下的均值−方差投资组合模型。李晨等[16]考虑了允许卖空情形下包含多约束的均值−绝对偏差投资组合模型。孙薇等[17]考虑允许卖空和不允许卖空的投资组合问题，建立了具有投资限制的模糊随机均值−方差投资组合模型。

在现实投资决策中，投资者通常需要不断地调整投资策略，即投资决策过程是多期的。Guo等[18]基于可信性理论研究资产具有不同投资期限情况下的投资组合问题，构建了一个带V型交易费用的多期模糊投资组合模型。Gupta等[19]研究了乐观与悲观情形下的投资组合问题，建立了多期直觉模糊投资组合选择模型。在实际投资过程中，当投资者的财富低于预定水平时，其将面临破产的情形，故有必要对破产事件的发生进行控制。徐维军等[20]构建了一个具有破产风险约束的多项目模糊投资组合模型。Liu等[21]提出了一个模糊环境下具有破产控制和反馈控制的多期投资组合模型。Cao[22]研究了一种基于破产风险控制的多期模糊投资组合模型。

本文研究模糊环境下考虑限制性卖空的多期投资组合优化问题。假设投资者当前持有一个资产组合，计划连续投资若干期，在每期期初将财富重新分配于各资产上。考虑到现实证券交易中存在卖空操作，因此允许投资者在投资过程中进行有一定限额的卖空交易。首先，将资产收益视为梯形模糊数，用可信性期望和下半方差分别度量资产组合的收益和风险。其次，引入单期最低期望收益约束、破产控制约束与投资比例边界约束等约束，以最大化终端累积财富和偏度、最小化终端累积风险为目标，构建考虑限制性卖空的多期可信性均值−下半方差−偏度投资组合优化模型，并采用加权极大−极小模糊规划方法将该模型转化为单目标规划模型。然后，设计一个多种群粒子群算法进行求解。最后，利用真实股票数据进行数值算例分析，说明所提出的优化模型及求解算法的可行性和实用性。

1 预备知识

本节简要地介绍本文所涉及的模糊数学相关知识。

对于任意的x ∈R，隶属函数µ(x)表示模糊变量ξ=x的可能性。若模糊变量ξ的隶属函数µ(x)满足如下形式

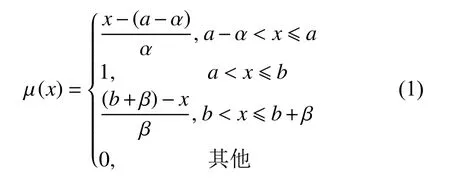
则称ξ为梯形模糊数，记为ξ=(a,b,α,β)。

定义1[23]设模糊变量ξ的隶属函数为µ(x)。对于任意的γ ∈(0,1]，称集合{x ∈R:µ(x)≥γ}为模糊变量ξ 的γ水平截集。

易知，梯形模糊数ξ=(a,b,α,β)的γ水平截集为

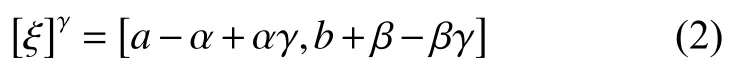
定义2[10]对于任意的r ∈R，模糊事件{ξ ≤r}的可能性、必要性与可信性分别定义为

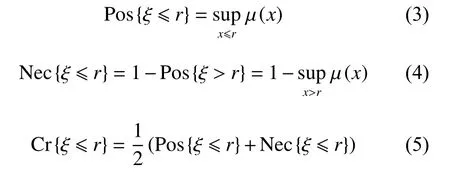
称Pos、Nec与C r分别为可能性、必要性与可信性算子。

容易看出， Cr具有自对偶性，即Cr{ξ ≤r}+Cr{ξ ＞r}=1。

对于梯形模糊数ξ=(a,b,α,β)，模糊事件{ξ ≤r}的可信性为

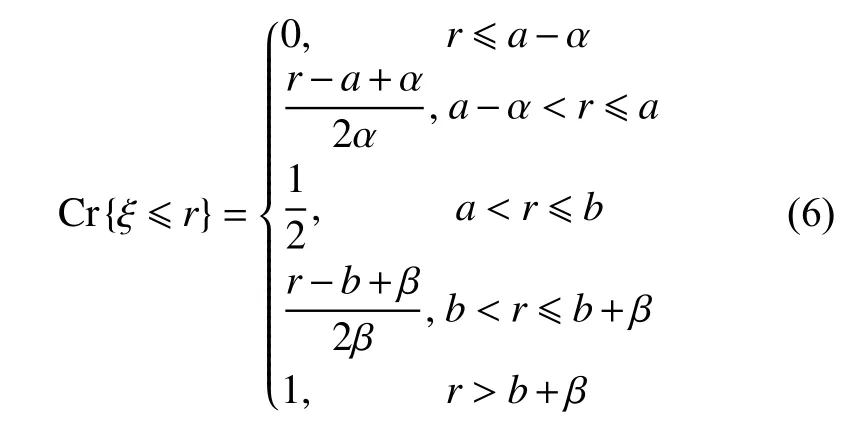
引理1[23]设ξ=(a1,b1,α1,β1) 和η=(a2,b2,α2,β2)为两个相互独立的梯形模糊数，ρ 为实数，则有

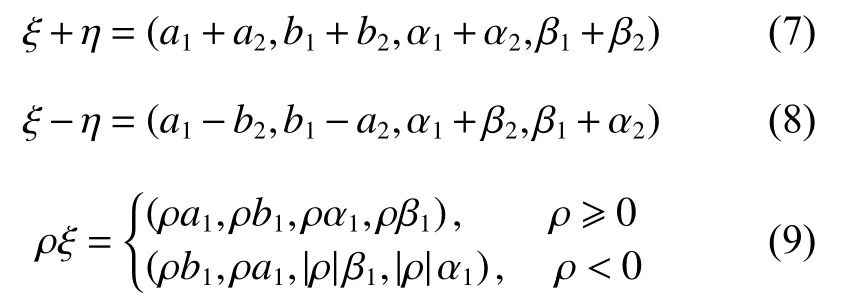
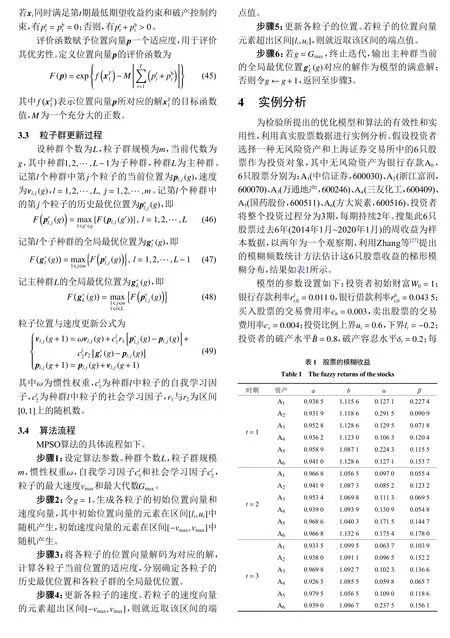
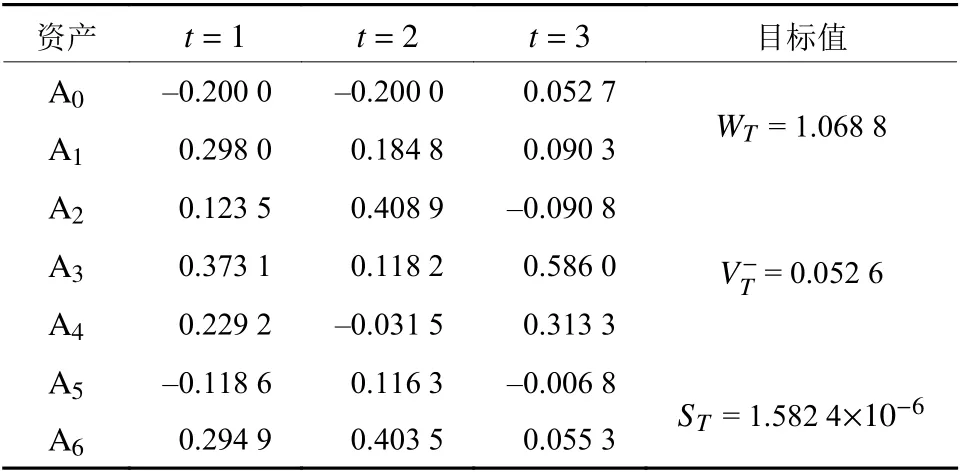
表2 投资组合的最优投资策略Table 2 The optimal investment strategy of the portfolio

图2 MPSO与PSO算法的收敛过程Fig.2 The convergence processes of the MPSO and PSOs

图3 MPSO算法在4次测试中的收敛过程Fig.3 The convergence processes of the MPSO in four tests

由图2可知，MPSO算法所得到的解最佳，PSO算法在5次运行中的收敛结果不稳定。这说明了MPSO算法与PSO算法相比具有更好的性能。由图3可知，MPSO算法在4次测试中的收敛结果差异较小，说明该算法具有较好的稳定性。综上所述，MPSO算法可以有效地求解复杂优化问题，且稳定地保持良好的性能。

为讨论投资比例边界约束对投资决策的影响，利用所设计的算法分别对具有不同投资比例上界和下界的投资组合模型进行求解，结果如表3和4所示。

表3 不同投资比例上界u i下的最优投资策略(li=−0.2)Table 3 The optimal investment strategy under different upper bounds ui of the portfolio (li=−0.2)

由表3可知，当投资比例上界较大时，投资者可选择的策略相对较多，其更倾向于集中投资少量股票，所获得的终端累积财富较多，且终端累积偏度较大；当投资比例上界较小时，投资者可选择的策略相对较少，其更倾向于选择较为分散的投资策略，所承担的终端累积风险较小。由表4可知，当投资比例下界较小时，特别是允许卖空操作时，投资者可选择的策略相对较多，其更倾向于卖空资产，所获得的终端累积财富较多，且终端累积偏度较大；当投资比例下界较大时，投资者可选择的策略相对较少，其更倾向于选择较为保守的策略，即较少或不进行卖空操作，所承担的终端累积风险较小。

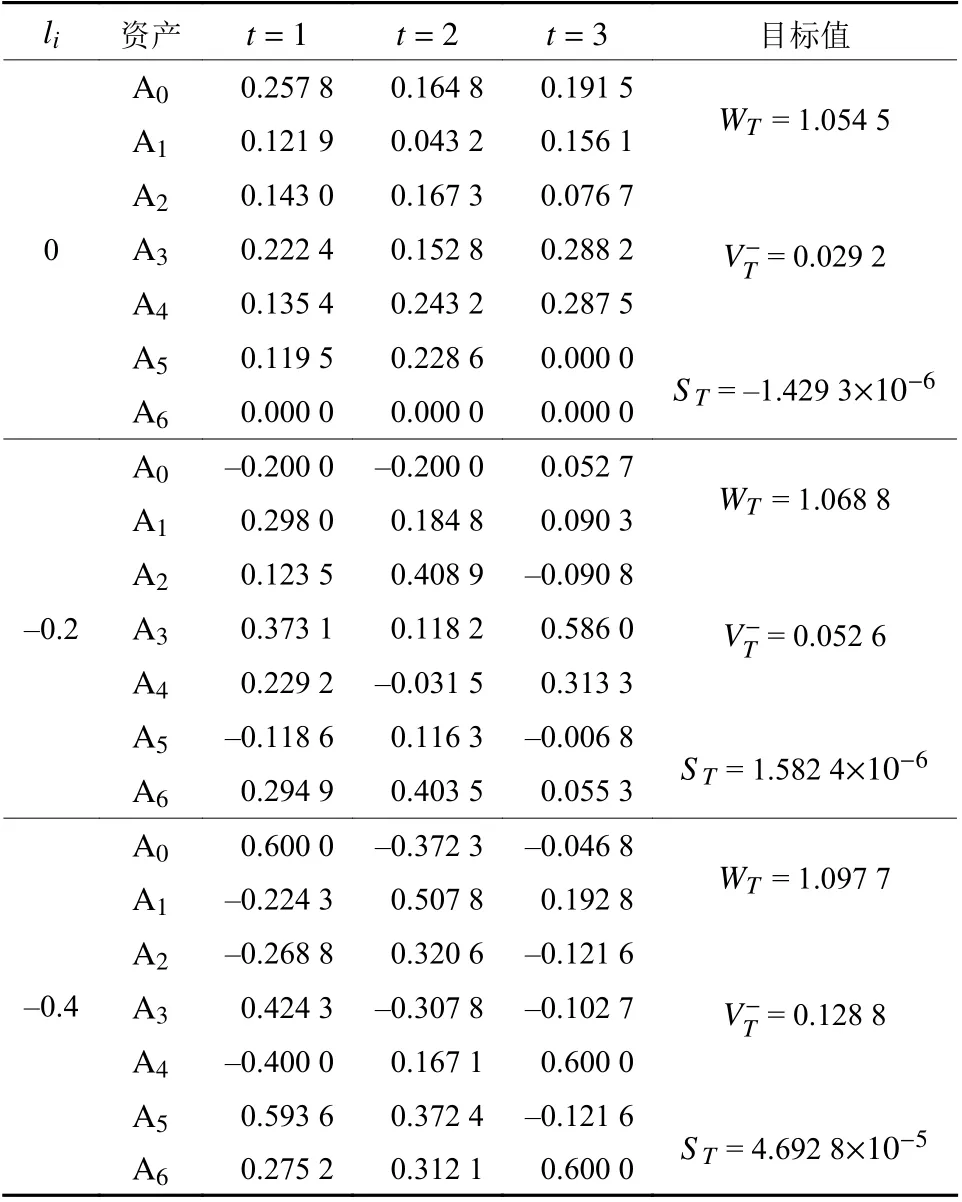
表4 不同投资比例下界li下的最优投资策略(ui=0.6)Table 4 The optimal investment strategy under different lower bounds li of the portfolio (ui=0.6)

为讨论不同目标偏好对投资决策的影响，求解不同目标权重下的模型 P5，结果如表5所示。

由表5可知，不同权重偏好的投资者的最优投资组合策略不同。当投资者看重终端累积财富时，会赋予财富目标较高的权重，其所获得的终端累积财富较多；当投资者看重终端累积风险时，会赋予风险目标较高的权重，其所承担的终端累积风险较低；当投资者看重终端累积偏度时，会赋予偏度目标较高的权重，其所构建的投资组合的终端累积偏度较高。因此，本文所提出的模型可以有效地为不同目标偏好的投资者提供决策支持。投资者可以根据自身需要，灵活地选取模型中各个目标的权重。

5 结论

考虑到卖空交易是金融市场上常见的一种投资行为，本文建立了考虑限制性卖空的多期模糊均值−下半方差−偏度投资组合优化模型，并设计了一个多种群粒子群算法进行求解。同时，利用真实股票数据进行实例分析，说明了所设计算法具有良好的性能和稳定性，所构建的多期模糊投资组合模型可以为投资者提供决策支持。在实际投资过程中，存在许多影响投资决策的现实因素，本文仅考虑了限制性卖空与交易费用，未来拟对考虑更全面的现实因素的多期模糊投资组合问题作进一步探讨。

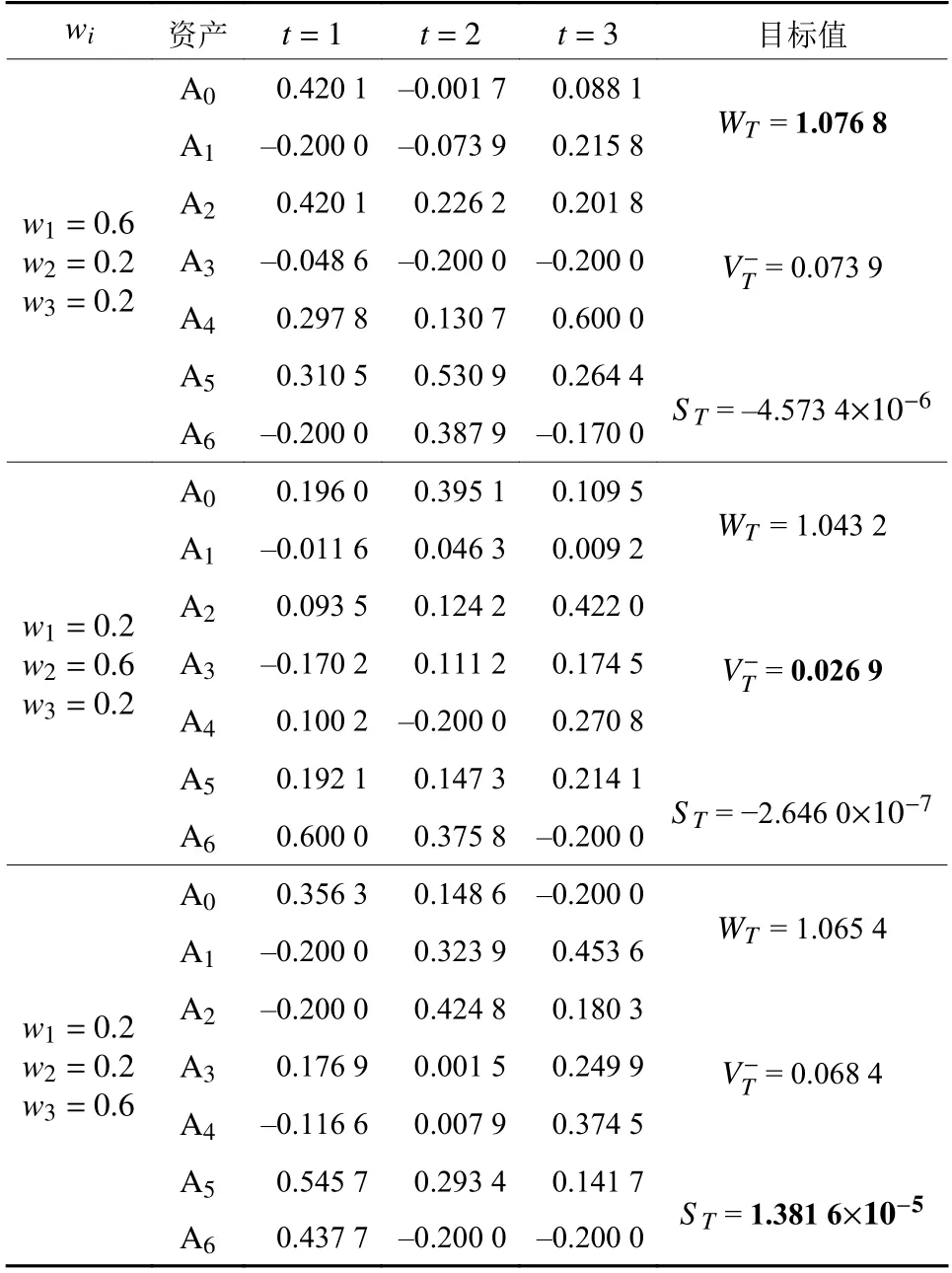
表5 不同权重下的最优投资策略Table 5 The optimal investment strategy under different weights