一个具有Robin自由边界的双曲肿瘤生长模型解的定性分析

周 云，卫雪梅

（广东工业大学 应用数学学院，广东 广州 510520）

1 问题的提出

有关于肿瘤生长的偏微分模型的方程类型总共有3类：一类是Byrne-Chaplain型肿瘤模型，只含反应扩散方程；另一类是King-Ward型肿瘤模型，既含反应扩散方程又含守恒率方程；以及流体型肿瘤模型，不仅含有以上两类方程而且还含有Stokes方程[1](由Franks等[2-5]提出)。本文研究的模型属于King-Ward型肿瘤模型，该模型的肿瘤来源于实验室，专门培育出来用于研究肿瘤生长问题[6-7]。该模型由关于繁殖细胞密度、休眠态细胞密度以及死细胞密度的一阶双曲方程组，一个关于营养物浓度的椭圆方程和用来描述肿瘤自由边界运动的常微分方程所耦合的自由边界问题。在营养物浓度是线性反应扩散方程和Dirichlet边界条件下，文献[8-10]得到了整体解的适定性和肿瘤半径的一些性质。

肿瘤的生长依赖于新生血管，当肿瘤细胞分泌生长因子时，会促进血管的再生。而新生的肿瘤血管组织，仍然可以作为输送途径吸收营养物[11-12]，因此本文假设

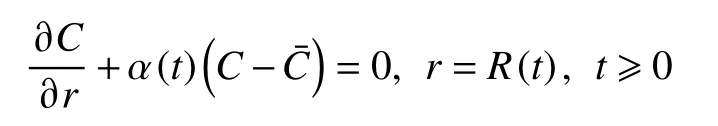
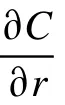
本文在前述文献的基础上，考虑营养物浓度C为线性椭圆方程的Robin问题。该模型中描述肿瘤细胞生长的两个双曲型偏微分方程，包含繁衍态的肿瘤细胞密度 P 、休眠态的肿瘤细胞密度 Q和已经死亡但尚未消解的肿瘤细胞密度 D[1], N代表这3类细胞混合体的密度且为正常数，有

细胞在肿瘤内做连续运动，其中包括细胞的增殖和细胞的坏死。本文用速度场v表示此运动速度，将肿瘤组胞视为多孔介质，因此根据Darcy’s定律，有

假设肿瘤表面的压力即表面张力，则在细胞边界处有

σ=γκ

其中κ表示平均曲率，γ 为正常数。

本文研究的具体模型为

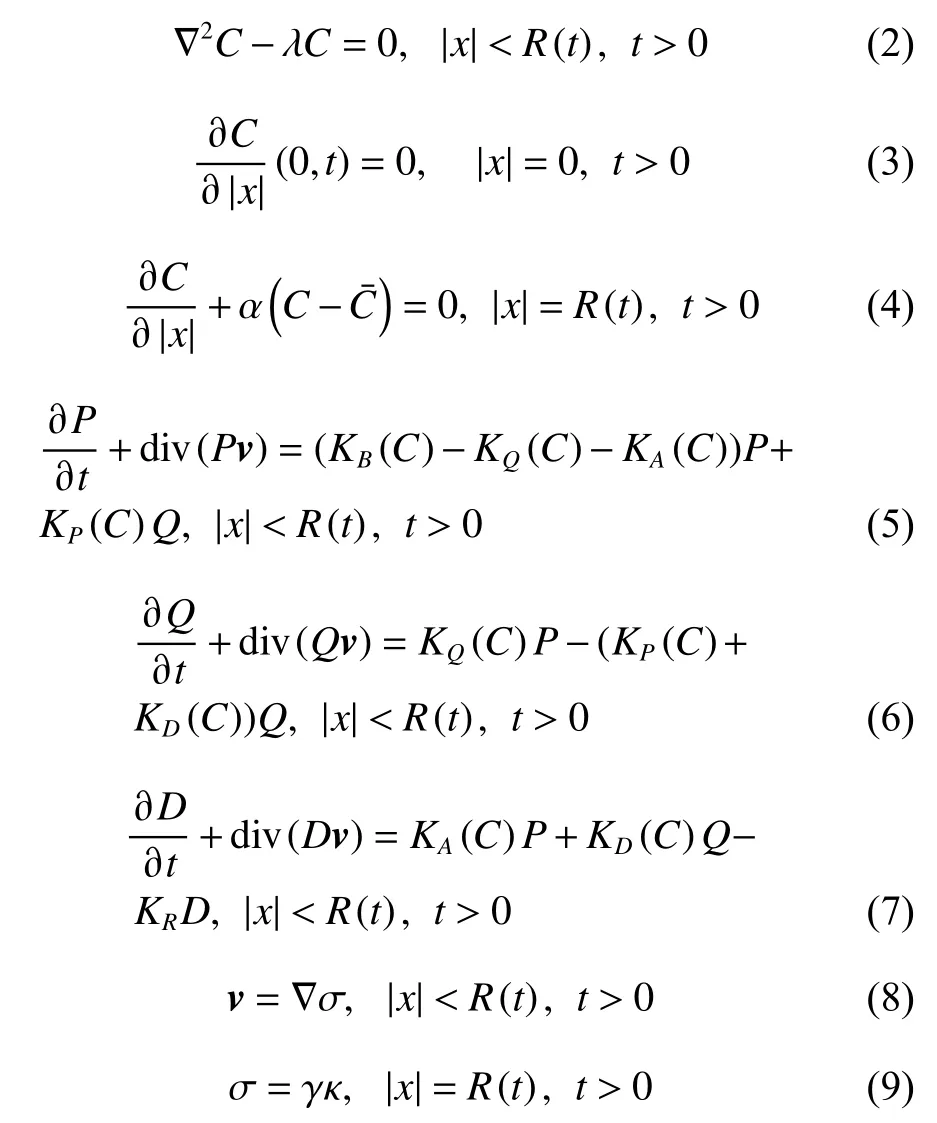
其中λ是非负常数,|x|≤R(t) (x ∈R3)表示肿瘤在时刻t所占的空间区域，KB(C), KP(C), KQ(C)分别表示繁衍态细胞的繁殖速率，休眠态细胞变为繁殖细胞的转换速率和繁殖细胞变为休眠态细胞的转换速率，KA(C) 和KD(C)分别表示繁衍态细胞和休眠态细胞的死亡速率[1]，其中KB(C), KP(C)随着C 的增大而增大，K(C), K(C), K(C)随着C 的增大而减小。另外，由于增殖率大于凋亡率，所以KB(C)＞KA(C)。 KR表示死亡细胞的消解速率，这个速率是一个非负的且与C 无关的常数[8]。

由式(8)～(9)可得，只要给定了v和R(t)，则σ 能够直接被确定，因此在本文后面的计算中忽略σ 。

给定初始条件

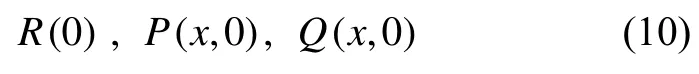
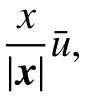
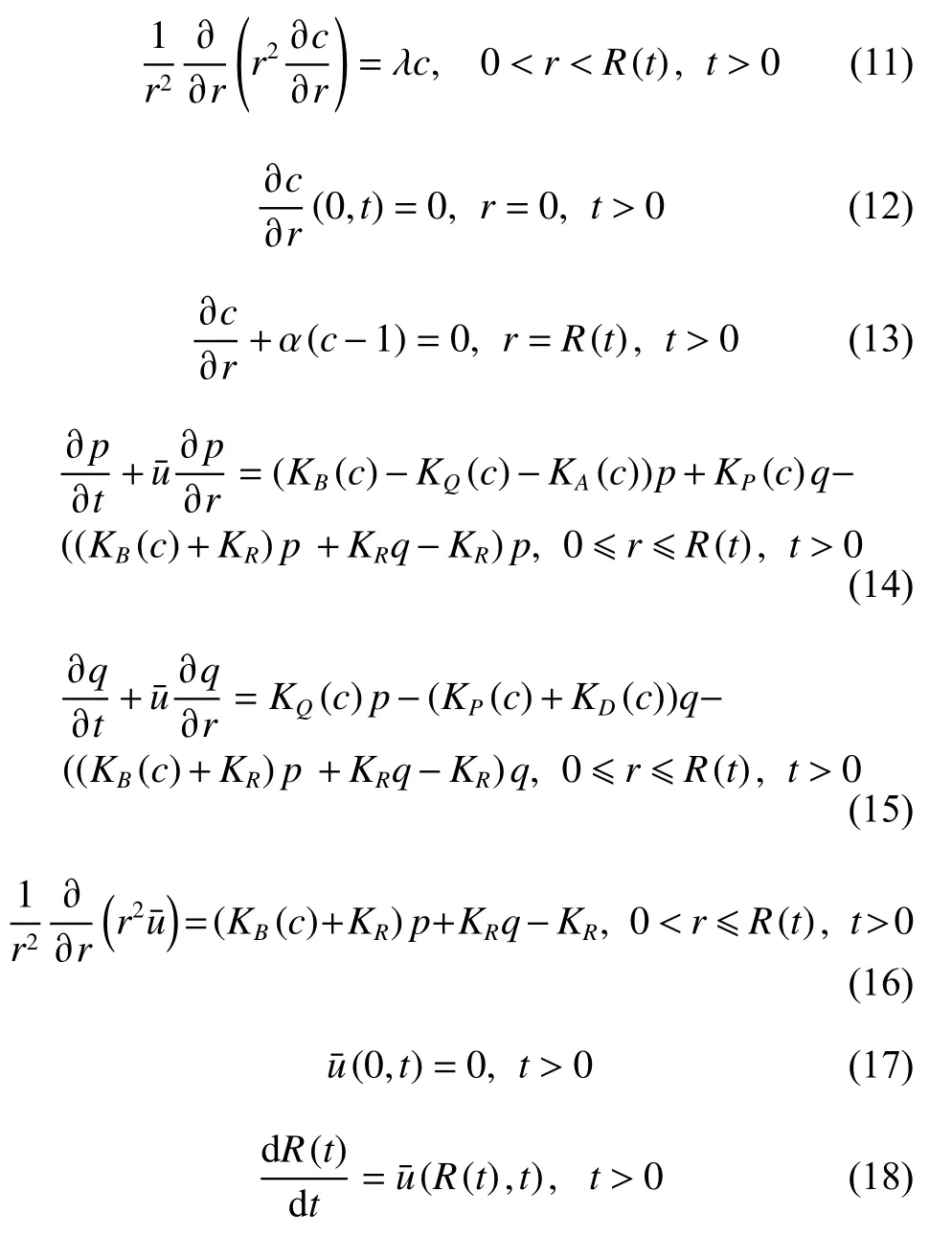
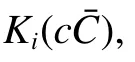
在本文的第2节中，将径向对称问题转换为固定域中的方程组。在第3～4节中，证明了方程组整体解的存在性和唯一性。最后，在第5节中，考虑一个特殊情况：肿瘤中的死亡细胞根本没有消解，即KR=0,并证明了当t →∞时，有R(t)→∞。

2 转换方程组

为了能够更简便地求解以上方程组，本文将其转换为一个与之等价的固定区域进行求解。考虑营养物浓度的方程及边界条件[12]，可得