可靠度理论在边坡工程中的应用研究

张凌晨，白建强，侯瑞凯，卿菁，卢应发

(1 湖北工业大学 土木建筑与环境学院，湖北 武汉 430068；2 中铁大桥局第七工程有限公司，湖北 武汉 430050；3 大连理工大学工程抗震研究所，辽宁 大连 116024)

不确定性普遍存在于自然界，同时也存在于各类工程中。边坡工程中存在众多具有显著随机性的影响因素，如岩土体的强度、边坡的应力场、渗流场、荷载作用机制等。为了保证边坡的安全性并对边坡的变形进行及时的预测预报与治理，有必要研究边坡稳定程度的不确定性[1]。

在工程建设中，随机性是较为常见的不确定性形式，一般用概率体现其大小。随着概率与统计理论的发展，工程结构的可靠性理论快速进步，至今形成了空前完整的可靠性理论规范体系。可靠性理论使用安全影响因子的概率分布描述工程结构的可靠性[2]。这种方法以一个确定的概率值来描述工程结构中的不确定性，为工程结构可靠性提供了一个定量的衡量标准[3]。由于边坡工程的复杂性与各类安全影响因素的不确定性，可靠性理论在边坡领域具有较为广阔的应用与发展前景[4-6]。

目前，已有许多学者对边坡稳定可靠性进行了研究。关于边坡可靠性的研究取得了许多成果。文献[7-13]应用蒙特卡洛方法研究了边坡可靠性，得出了许多有益于边坡可靠性理论发展的结论。文献[14-19]应用一次二阶矩方法研究了边坡可靠性，提出了许多边坡可靠性研究的新思路。文献[20]采用罗森布鲁斯法计算了实例滑坡的可靠指标。

然而，目前边坡可靠性研究尚未形成较成熟的理论体系，可靠性理论并未在边坡工程中获得广泛应用。因此，本文将结构可靠性基本原理运用于边坡可靠性分析，分别采用蒙特卡洛模拟方法、一次二阶矩方法与罗森布鲁斯方法与现行的边坡极限平衡法相结合的方式对边坡可靠性进行计算并对计算结果进行比较分析，以探究更为合理的边坡稳定性预测预报方法，从而为滑坡的防治工作提供更高效、更明确、更完善的指导方法。

1 边坡可靠度原理

1.1 边坡可靠性功能函数

类似结构可靠性，边坡可靠性可用边坡的抗力与荷载作用效应之差作为功能函数，即边坡的抗滑力与下滑力之差，强度储备表示的功能函数为：

Z=R(X1,X2,…,Xn)-S(X1,X2,…,Xn)

(1)

与式(1)对应的破坏概率为：

(2)

根据边坡可靠性分析的特征，可采用传统稳定系数进行状态判断。即安全系数表示功能函数：

(3)

与式(3)对应的破坏概率为：

(4)

边坡的可靠度为：

PS=1-Pf

以上各式中，R表示抗滑力；S表示下滑力；Xi(i∈(1,n))表示与边坡稳定性相关的随机变量；g(r,s)表示抗力与下滑力的联合概率密度；fZ(z)表示功能函数的概率密度。

1.2 边坡可靠性指标

如果功能函数服从正态分布，则对应于上述两种功能函数有两种可靠指标。将功能函数标准化后代入式(2)可得：

因此，强度储备功能函数对应的可靠指标为：

当只考虑粘聚力c与摩擦常数f的变异性时，安全系数为c、f的线性组合。因此，当c、f服从正态分布时，安全系数Z仍服从正态分布[21]。将功能函数标准化后代入式(4)可得：

因此，安全系数功能函数对应的可靠指标为：

其中，μZ为Z的均值；σZ表示标准差；β为可靠指标。

2 边坡可靠度计算实例

某岩质边坡的截面尺寸特征及荷载如图1所示，纵向长约200 m，故可视为平面应力问题。其抗剪强度参数c，f具有较为显著的变异性，因此可视为随机变量。本实例的重度γ=10 kN/m2，变异性很小，对边坡可靠性的影响比强度参数小许多，故可视为常量[22]。坡体及滑动面的抗剪强度参数如下：μc=106 kPa，σc=33 kPa，δc=0.31，μf=0.2924，σf=0.0209，δf=0.07，ρc, f=0。目前多数研究仍认为岩土材料的强度指标服从正态分布或对数正态分布[23]，故设参数c，f服从正态分布。

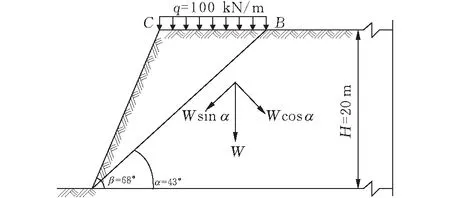
图 1 边坡截面图

基于三种可靠度计算方法，分别采用式(1)和式(3)所示的两种边坡功能函数。针对不同均布荷载作用条件下的边坡可靠度及其安全系数均值μF进行计算分析。q由图1所示的初始状态逐级递增，每一级的增量为50 kN/m，直到q增加至600 kN/m为止。此三个力的作用点应位于O点处。基于上述两种功能函数，可得到上述实例边坡相应的的状态方程分别为：

强度储备功能函数的状态方程：

Z1=g1(c,f)=R(c,f)-S(c,f)=
clAB+(W+qlBC)cosα·f-
(W+qlBC)sinα=0

(5)

安全系数功能函数的状态方程：

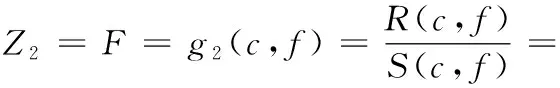
(6)

其中，c为坡体粘聚力；f表示摩擦常数；W为重力，lAB表示AB边的长度；lBC为BC边的长度。

3 蒙特卡洛法计算

采蒙特卡洛法的基本原理见文献[24]。其特点为：既考虑了边坡可靠度的众多影响因素，又避免了复杂困难的数学计算，其原理易程序化，但计算结果受抽样方式与模拟次数影响。设绝对误差不超过1%，置信度为99%，则由文献[17]可知，模拟次数约大于或等于65 895次，可满足要求。运用Matlab软件编写程序，分别以式(1)和式(3)为功能函数，进行10次～5×108次模拟计算。在q=100 kN/m的条件下，计算结果如表1所示。由于两种功能函数模拟结果相同，故表1不再区分功能函数形式。

由表1数据可知，当模拟次数达到107次后，边坡破坏概率和可靠度趋于稳定值。而要满足误差小于1%的条件，只需模拟65 895次以上便可。因此在判断错误的概率趋于0的条件下，可认为5×108次模拟计算所得的可靠度是所用模型计算的真实可靠度。

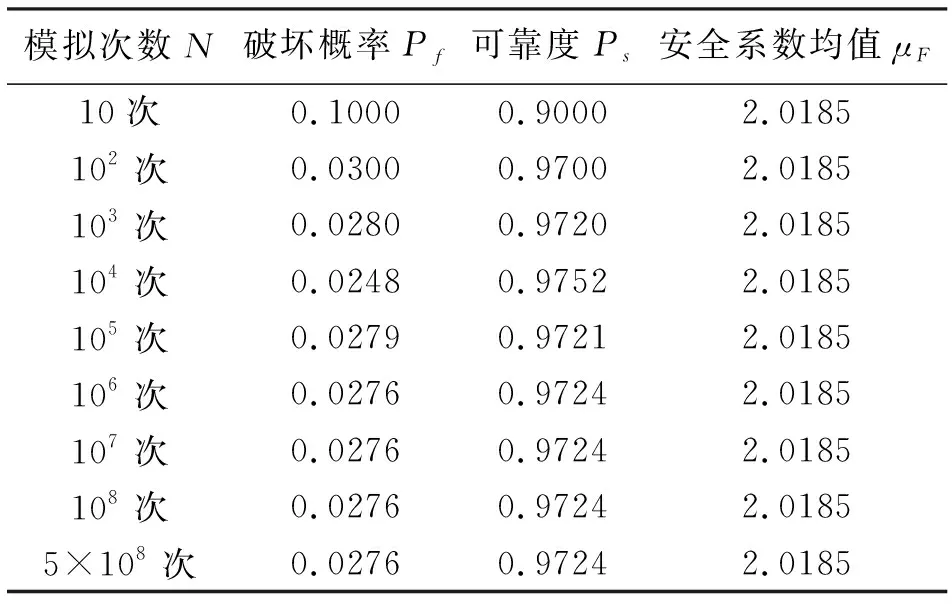
表1 不同模拟次数下的可靠度

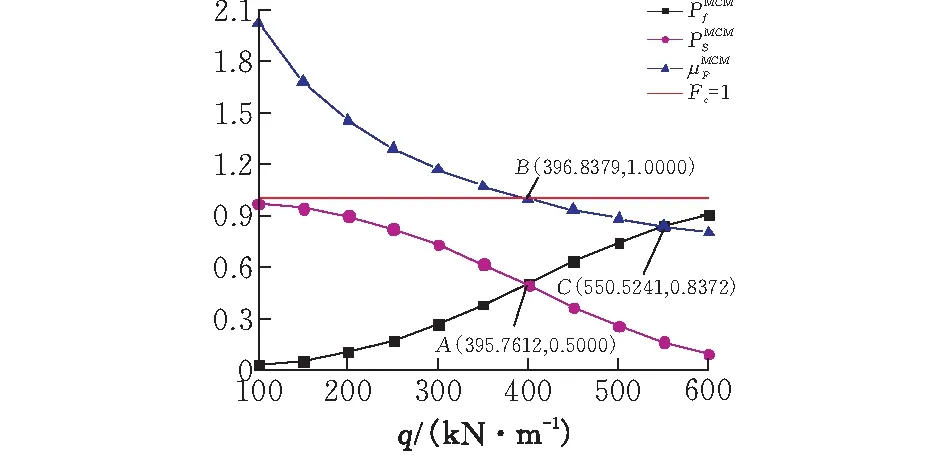
图 2 不同荷载下的蒙特卡洛法可靠度

据图2显示，在初始的坡顶均布荷载作用下边坡的破坏概率为0.0276，可靠度为0.9724，极限平衡法稳定系数均值为2.0185,边坡处于稳定状态。当坡顶均布荷载的级别越来越大时，边坡的破坏概率也逐级递增，整体可靠度和极限平衡法的整体稳定系数期望值逐级递减。在破坏概率与可靠度随荷载级别变化曲线的交点A处二者相等皆为0.5，对应的安全系数均值十分接近B点临界安全系数Fc=1.0。随着均布荷载的增加，当荷载在350 kN/m～450 kN/m范围内变化时，边坡的可靠度下降程度比其他荷载对应的阶段显著。对应的稳定系数均值变化范围为1.0713～0.9336。当稳定系数均值由1.0713逐渐减小时，传统观点认为边坡处于基本稳定状态，但十分接近欠稳定状态，从破坏概率上看仍然有较大的破坏可能性。当稳定系数均值减小至0.9336时，传统观点认为，边坡已发生破坏，但从可靠度上看边坡仍然有较大的不发生破坏的可能性。对于C点，稳定系数均值判定边坡处于严重破坏状态，但依概率仍存在不发生破坏的可能性。蒙特卡洛法很好地模拟了算例边坡应力状态更替过程中的可靠度及破坏概率的动态演化规律。

4 一次二阶矩中心点法计算

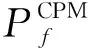
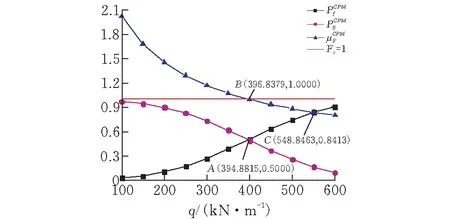
图 3 不同荷载下的一次二阶矩中心点法可靠度

从图3可以看出，在初始的坡顶均布荷载作用下，边坡的破坏概率为0.0276，可靠度为0.9724，极限平衡法稳定系数均值为2.0185，边坡处于稳定状态。当坡顶均布荷载的级别越来越大时，边坡的破坏概率也逐级递增，整体可靠度和极限平衡法的整体稳定系数期望值逐级递减。当破坏概率与可靠度相等时，对应的荷载级别几乎与极限平衡法的整体稳定系数均值为1的临界点所对应的荷载级别重合。随着均布荷载等级逐渐均匀地增加，当荷载在350 kN/m～400 kN/m范围内增长时，边坡的可靠度下降较显著，且破坏概率增长较明显；极限平衡法的整体稳定系数的数学期望虽大于1，但十分接近欠稳定状态。当荷载在400 kN/m～450 kN/m范围内增长时，边坡破坏概率已超过50%，有破坏的可能性较大；此时边坡已失去充足的抗力，但仍有一定的可靠度。当荷载级别到达C点时，依据极限平衡稳定系数，边坡早已形成滑坡。但依概率仍存在维持现状稳定的几率。一次二阶矩中心点法较好地体现了荷载逐级递增过程中案例边坡的可靠度变化特征。

5 罗森布鲁斯法计算

5.1 罗森布鲁斯法基本原理

罗森布鲁斯法的基本原理如下[26]：

首先，计算将式(1)或式(3)所示的功能函数的各阶原点矩E(Zk)：

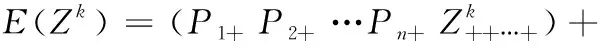
(7)

式(7)中，对应于n个基本随机变量，功能函数Z有2n个取值。基本随机变量的样本值按下式确定：

正负偏度纠正系数分别为：

Pi-=1-Pi+

其中，CSXi表示偏度系数。一般情况下，若偏度系数未知时，通常先假设其为0。

如果基本随机变量Xi(i=1，2，…，n)互相之间具有相关性，则2n个功能函数Z值所对应的2n个基本随机变量样本值组合中每一组合的概率为：

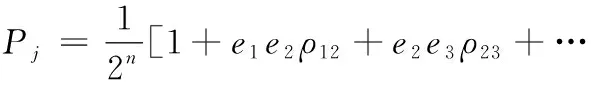
(8)

式(8)中，ρpq(p=1，2，…，n；q=1，2，…，n)为基本随机变量Xp与Xq之间的相关系数。ei(i=1，2，…，n)的取值按如下方法：

当Xi取xi+时，ei=1；

当Xi取xi-时，ei=-1。

对应于n个基本随机变量的样本值有2n个取值点，共有2n种组合方式，基于此，功能函数Z的均值的估计值为：

至此，可计算出与功能函数分布特征系数相关的前四阶中心矩。一阶矩，即均值

二阶中心矩，即方差

三阶中心矩

M3=E[(Z-μZ)3]≈

四阶中心矩

M4=E[(Z-μZ)4]≈

描述功能函数分布离散程度的变异系数

描述功能函数分布对称性即偏移程度的偏度系数

描述功能函数分布峰值高低的峰度

描述功能函数可靠性的可靠指标

该法的特点为：原理简单，条理清晰，易于程序化，且规避了功能函数的求导过程，极大简化了计算过程。

5.2 实例计算

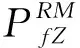
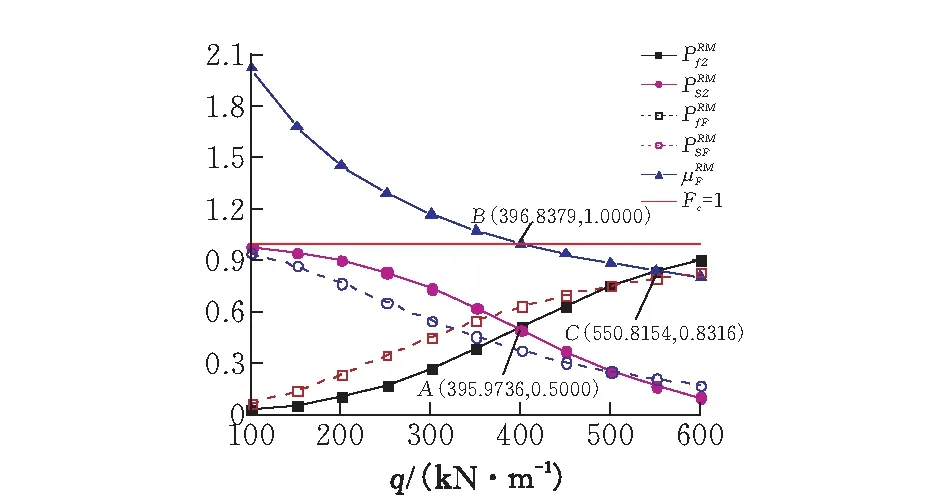
图 4 不同荷载下的罗森布鲁斯法可靠度

由图4可知，罗森布鲁斯法基于两种功能函数计算的两组可靠度与破坏概率数据在一般情况下(q≤400 kN/m)，差异较大。其中，基于式(1)和式(5)计算的可靠度比基于式(3)和式(6)确定的可靠度大，基于式(1)和式(5)计算的破坏概率比基于式(3)和式(6)确定的小。在边坡破坏概率超过75%，q=500 kN/m等级以上荷载作用下的少数极端情况下才会出现基于安全系数功能函数的可靠度略大于强度储备功能函数计算的可靠度，基于安全系数功能函数的破坏概率略小于强度储备功能函数计算的可靠度的情况。

6 计算结果比较

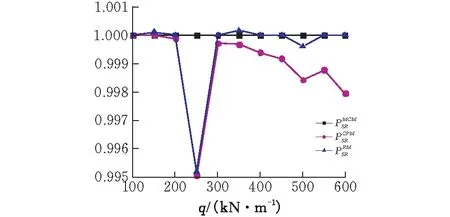
图 5 不同方法的相对可靠度

根据图5可得，总体上，一次二阶矩中心点法计算的实例边坡可靠度小于基于强度储备功能函数式(1)的罗森布鲁斯法计算的可靠度小于蒙特卡洛法的计算结果。三者计算结果的差异十分微小，数值上相差不超过0.5%。

7 结论

将传统的平面剪切破坏分析法与随机可靠度方法相结合，研究了边坡在渐进破坏过程中稳定可靠性的演化规律。并对不同随机可靠度模型模拟的结果进行了比较。得出如下的结论：

1)采用可靠性方法克服了传统极限平衡法的定值稳定系数法不能解释稳定系数大于1时，坡体变形失稳和稳定系数小于1时，坡体不失稳现象的缺点。同时，也证实了边坡稳定系数存在不确定性。

2)蒙特卡洛法用于边坡可靠度和破坏概率的计算具有较高的精度，能够较好地描述应力状态演化过程中边坡稳定性、可靠性及破坏可能性的变化规律，且不受功能函数数学表达形式的制约；可充分利用空前发达的计算机技术实现考虑多因素的超高次数模拟以获得更高精度的可靠度，在大数据时代的边坡稳定与可靠性评价及边坡工程数字化治理方面具有十分广阔的应用前景。

3)一次二阶矩中心点法用于计算边坡的可靠度不受功能函数数学表达形式的影响，能够较好地拟合荷载强度增长过程中边坡稳定性下降的趋势；此外，在计算边坡可靠度的过程中，既简化了计算，又保证了一定的精度，在功能函数分布复杂或未知分布的边坡可靠性评价方面具有较强的适用性。

4)罗森布鲁斯法应用于边坡可靠度的计算时，其结果与功能函数表达形式有关；但此法在功能函数复杂难求导或基本随机变量分布未知的边坡可靠性分析中具有显著优势。

5)这三种方法计算的可靠度和破坏概率均能够较好地模拟边坡变形失稳过程中稳定性与可靠性的动态演化特征。其中，罗森布鲁斯法采用安全系数功能函数计算的可靠度在实际应用中最安全。

6)在对边坡进行可靠度分析时，须明确边坡的岩性特征、几何参数、荷载条件及变形机理等重要因素。然后，基于此建立符合各要素分布特征的物理力学模型。全面结合边坡的各项特征选择与之具有良好契合性的可靠度分析方法，从而更好地对边坡的发展规律进行预测预报。