某型号配砟车动力学性能分析

张 超，李 帅，余 砥，张劲松，周明刚

(湖北工业大学农机工程研究设计院，湖北 武汉 430068)

配砟车是专门为道床的配砟整形开发的一种大型养路机械，其主要功能是在捣固和稳定作业施工后，通过对道床上的道砟进行分配、搬移、整形和清扫，以实现道床的配砟整形[1-2]。轨道工程车辆运行安全性是其设计研发的核心问题，动力学特性分析是研究轨道车辆运行安全性的常用技术手段。Lee,Jin-Ho等[3]建立了混合动力列车模型，并采用SC-LSM技术，研究了模型磁刚度对列车运行稳定性的影响。罗仁等[4]用数值计算方法分析了列车运行的平稳性，认为横向连接阻尼和刚度对列车横向平稳性影响显著。刘宏友等[5-6]利用列车动力学分析软件TVDYNA1.0、常微分方程一次近似理论及Hopf分叉理论，重点研究了列车的非线性运行稳定性。周劲松等[7]采用面向对象的建模技术建立了带车辆间悬挂系统的三辆车编组以及单车的垂向及横向非线性动力学模型，研究表明加入悬挂系统增加列车高速运行时的平稳性。曾元辰等[8]利用改进的AGREE可靠度分配算法研究列车运行的稳定性。

本文以某型号配砟车为研究对象，基于多体动力学法，采用牛顿-欧拉方程构建其数值模型，依据GB/T 17426-1998[9]，以运行平稳性、运行稳定性和曲线通过性为衡量指标，对该配砟车的动力学性能进行分析，对其运行安全性进行校核计算。

1 配砟车动力学仿真模型

多体动力学法是研究列车动力学性能的常用方法，对于列车模型的构建常采用牛顿-欧拉动力学法。牛顿-欧拉动力学法将列车看成由多个刚体部分通过弹簧阻尼单元连接组成的多体系统(图1)。图1中，MC、Mb分别为车体质量之半和构架质量之半；K1、K2分别为一系和旁承的一侧的垂向刚度；C1、C2分别为一系和旁承一侧的垂向阻尼；V为车辆运行速度；XC、Xb1、Xb2分别为车体、前构架和后构架的垂向位移；βc、βb1、βb2分别是车体、前构架和后构架的点头角位移；Xr1～Xr4为轨道不平顺位移输入。

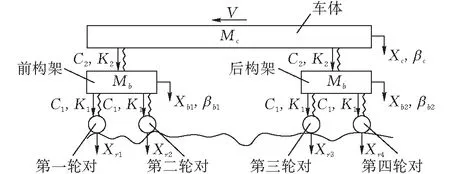
图 1 配砟车二维拓扑结构

根据图1的配砟车二维拓扑模型，由牛顿第二定理构建配砟车的运动方程[10]：

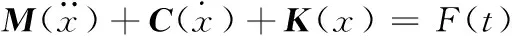
(1)

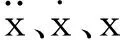
采用四阶龙格-库塔数值积分法对整个运动方程矩阵进行求解，即可得到配砟车的振动响应。

依据上述多体动力学理论，采用多体动力学软件Simpack，建立某型号配砟车仿真计算模型(图2)。该型号配砟车相关参数如表1所示。模型主要有车体1个、转向架构架2个、轮对4个和轴箱8个。车体、轮对和转向架构架各有6个自由度，轴箱的自由度为1，整个机车系统共计50个自由度。其中一系悬挂采用的是无间隙的弹性悬挂系统，可使配砟车具有良好通过性能及行车稳定性能。在该型号配砟车模型中，车体、轮对和转向架的连接方式为铁路铰接，车轮踏面类型为LM型，钢轨类型为50轨类型。

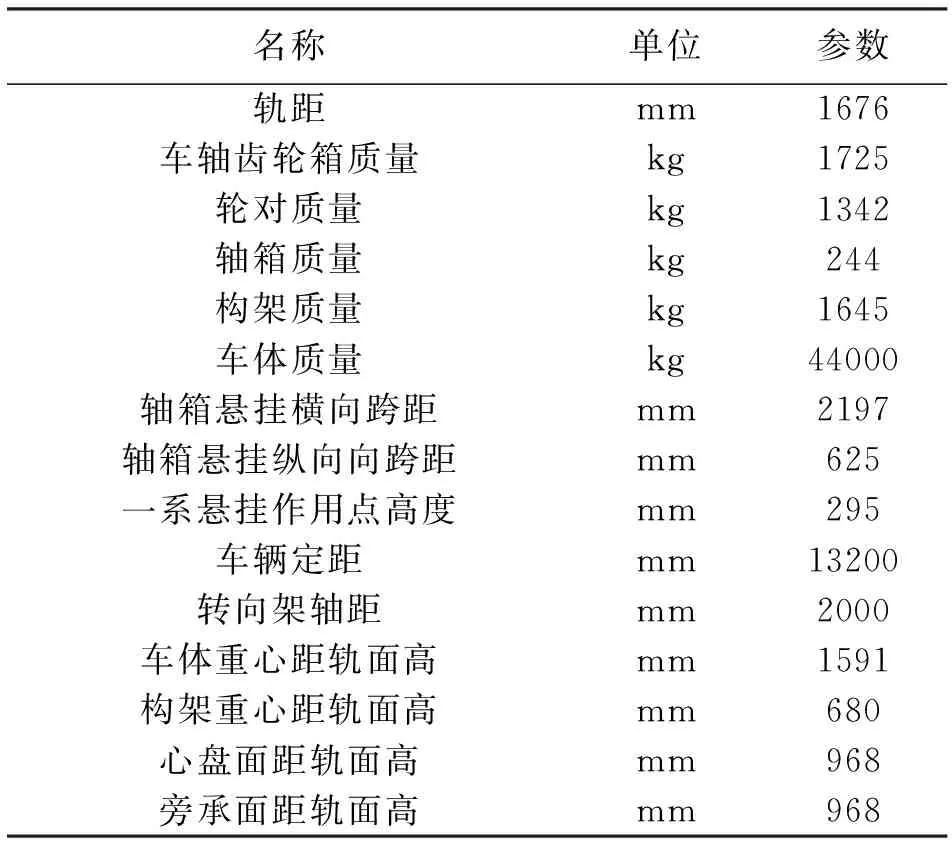
表1 配砟车结构参数

图 2 配砟车多体动力学模型

2 配砟车动力学性能

车辆的动力学性能主要包括运行稳定性、运行平稳性和曲线通过性等三项内容[11]。本文以上述三项性能指标，结合国家标准GB/T 17426-1998内容，对该型号配砟车的动力学性能进行分析计算。

2.1 配砟车运行稳定性

运行稳定性是防止车辆蛇行运动的重要衡量指标，其研究方法是使用四阶龙格-库塔数值积分法对配砟车多体动力学运动方程在外界激励条件下进行求解，分析车辆在不同运行速度下第一轮对和第三轮对的横向位移随时间的变化情况。如果其横向位移收敛则车辆运行时是稳定的，发散则处于失稳状态；当横向位移既不发散也不收敛，则此时对应的速度为车辆的非线性临界速度。如果车辆的非线性临界速度高于最高设计运行速度，则说明车辆运行稳定性满足运行要求[11]。

配砟车运行过程中的激励是由轨道线路不平顺引起的。美国联邦管理局FRA根据大量实测资料得到线路不平顺功率谱密度，并将其拟合成了一个以阶段频率和粗糙度常数表示的偶次函数，据此将轨道分为6个等级，即：Ⅰ级最差，Ⅵ级最好[10]。美国Ⅴ级线路轨道谱波长范围为1.524～304.8 m，与本文配砟车运行线路质量相当，因此计算过程中，以美国Ⅴ级线路轨道谱作为激励输入。配砟车运行线路总长度为10 000 m，激励施加到20～1000 m的线路上，分别对运行速度为100 、116 和117 km/h时配砟车第一轮对和第三轮对的横向位移随时间的变化进行了计算，结果分别如图3—5所示。

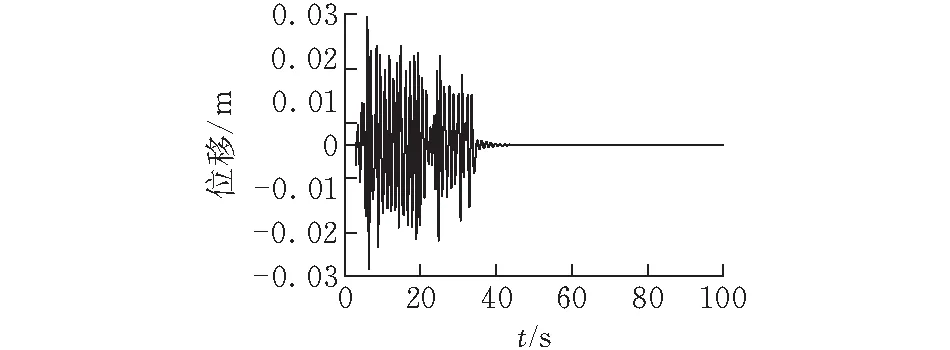
(a)第一轮对

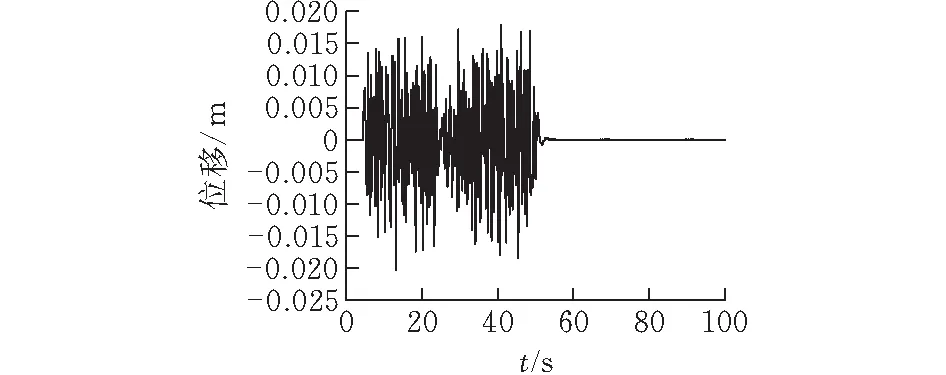
(a)第一轮对

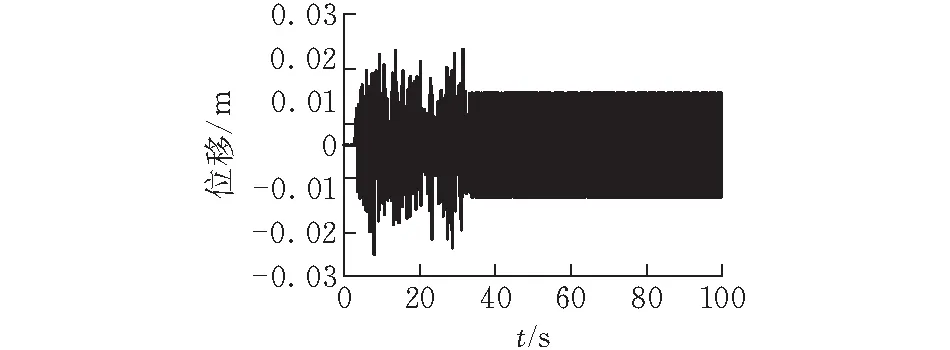
(a)第一轮对

从图5可以看出，配砟车行驶速度为117 km/h时，第一和第三轮对的横向位移出现稳定的周期振动，既不收敛也不发散，即车辆处于非收敛临界状态。图3和图4中配砟车行驶速度分别为100 km/h和116 km/h，可见当速度小于117 km/h时，第一和第三轮对的横向位移处于收敛状态。因此表明该型号配砟车的蛇行运动失稳临界速度Vcr为117 km/h，大于该型号配砟车最高设计速度100 km/h，且具有一定的速度裕量，说明该型号配砟车运行稳定性满足运行要求。

2.2 配砟车运行平稳性

运行平稳性主要反映了车辆本身的运行品质，同样采用四阶龙格-库塔数值积分法对配砟车动力学模型在美国Ⅴ级线路轨道谱激励条件下的动态响应进行求解，采用Sperling平稳性指标法可求出车辆的平稳性指标[11]。

W=(a3b3)1/10

(2)

(3)

式中：a是加速度幅值，b是加速度的计权系数，f为振动频率。

根据国家标准[9]，如果平稳性指标W小于3.0，则车辆的运行平稳性等级为优；若W在3.0～3.5之间，则其等级为良；当W处于3.5～4.0之间，则其等级为合格；而当W大于4.0，则不合格。分别提取配砟车运行过程中的最大横向加速度Ay和垂向加速度Az，当Ay小于4.905 m/s2，Az小于6.867 m/s2时，则车辆的运行平稳性符合运行要求。

依据式(2)分别对车辆运行速度为50～110 km/h配砟车的横向平稳性指标Wy及垂向平稳性指标Wz进行计算，并提取车辆的横向及垂向最大加速度Ay和Az，结果如表2所示。

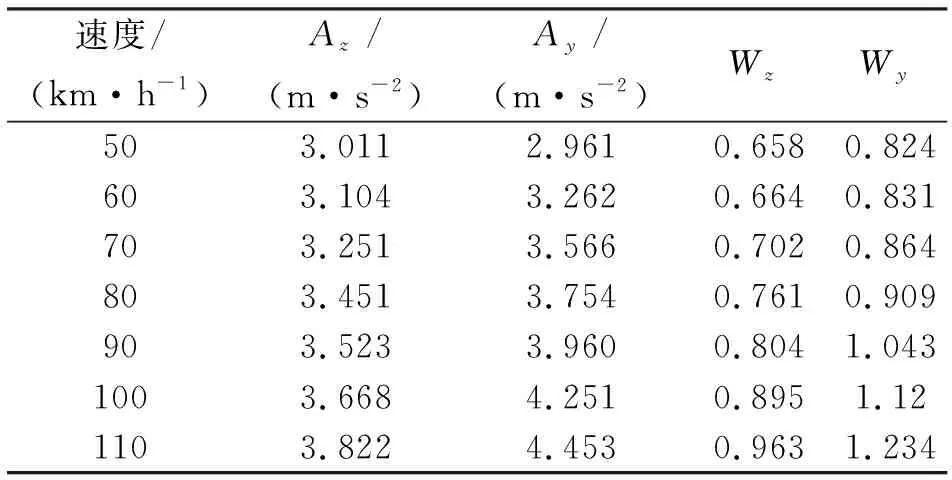
表2 配砟车运行平稳性计算结果

从表2可以看出，车辆运行速度为50～110 km/h速度范围内，配砟车的横向和垂向平稳性指标均小于3.0，属于GB/T1 7426-1998规定的优级标准，而且所有的最大横向加速度均小于4.905 m/s2，最大垂向加速度均小于6.867 m/s2。因此说明该型号配砟车运行平稳性满足运行要求。

2.3 配砟车曲线通过性分析

曲线通过性是关乎车辆运行安全性的重要衡量指标。车辆由直线驶入曲线时，特别是通过缓和曲线时，其受力特征将会出现明显变化。这一过程可以通过采用数值积分法对车辆通过有限长的曲线(特别是缓和曲线)时的响应进行求解分析，在此基础上计算出脱轨系数，并提取轮轴横向力，据此衡量车辆的曲线通过性[11]。

依据国家标准可知[9]，轮轴横向力容许限度Hmax为76.87 kN，且规定第一限度即危险限度脱轨系数为Q/P≤1.2，第二限度即允许限度脱轨系数为Q/P≤1.0，其中Q为爬轨侧车轮作用于钢轨上的横向力，P为爬轨侧车轮作用于钢轨上的垂向力。当车辆通过规定曲线时，其轮轴横向力H小于Hmax，且其脱轨系数Q/P最大值不大于1.2时，则可证明该型号配砟车的曲线通过性满足要求。

根据该型号配砟车实际运行情况，分析车辆曲线通过性时线路条件如下：

1)曲线半径R=300 m，曲线外轨超高h=95 mm，运行速度V=40 km/h；

2)曲线半径R=400 m，曲线外轨超高h=85 mm，运行速度V=45 km/h；

3)曲线半径R=500 m，曲线外轨超高h=80 mm，运行速度V=55 km/h；

4)曲线半径R=600 m，曲线外轨超高h=75 mm，运行速度V=60 km/h。计算结果如表3所示。从表3可见，配砟车在通过不同半径曲线时，其轮轴横向力H均小于轮轴横向力容许限度Hmax、脱轨系数Q/P均小于第一限度脱轨系数1.2，其曲线通过性满足要求。

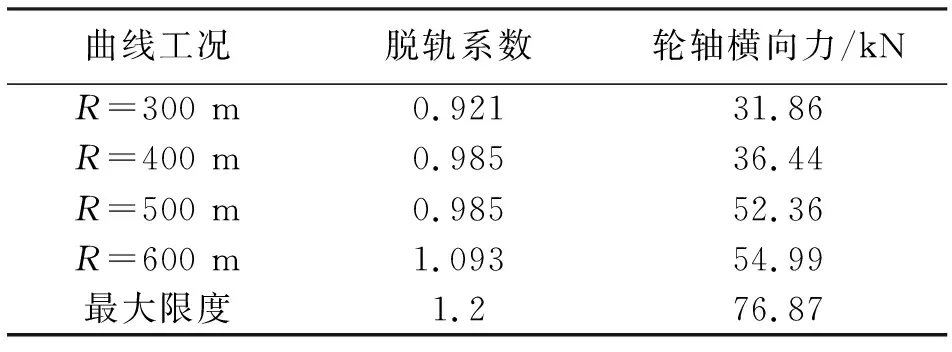
表3 配砟车曲线通过性

3 结束语

本文采用牛顿-欧拉方程，基于Simpack动力学软件建立了某型号配砟车的多体动力学模型。以此为基础，对该型号配砟车的运行稳定性、运行平稳性和曲线通过性进行了分析，所得具体结论如下：

1)该配砟车在美国Ⅴ级线路上行驶，其蛇行失稳临界速度为117 km/h，高于所设计的100 km/h的最高运行速度。

2)该配砟车在110 km/h速度内的横向和垂向平稳性指标小于3.0，满足有关国家标准规定的优级标准；在110 km/h速度范围内，配砟车的最大横向加速度小于4.905 m/s2，最大垂向加速度小于6.867 m/s2，均满足有关国家标准规定的要求。

3)该配砟车以40 km/h的速度通过半径为300 m的圆曲线、以45 km/h的速度通过半径为400 m的圆曲线、以55 km/h的速度通过半径为500 m的圆曲线以及以60 km/h的速度通过半径为600 m的圆曲线时，轮轴横向力H、脱轨系数Q/P均小于国家标准规定的最大限度值。

从上述研究结果可知，该型号配砟车各参数指标均符合国家标准GB/T 17426-1998规定，满足设计要求。