基于时域数据的两种低阶等效拟配方法研究
齐万涛, 吕新波, 武虎子
(航空工业第一飞机设计研究院, 西安 710089)
随着飞控技术的发展,阻尼器、增稳以及控制增稳系统的采用,飞机+飞控系统的组合系统的特征方程阶次急剧增加,尤其是含有反馈、前馈、成形滤波器和其他高频部件时,阶次可高达50~70阶[1]。众多的附加模态导致难以将飞机的纵、横航向模态相区分,无法按常规飞机的方法评价其飞行品质。但对于具有常规布局的飞机,它的响应过程近似于经典飞机的动力学特性,并且驾驶员往往对动态特性与经典飞机动态特性相似的高阶飞机给予好的飞行品质评价。基于这种情况,飞行品质规范建议采用等效拟配法仍将飞行品质沿用传统的品质规范进行评定。
频域等效拟配法求取等效系统参数是等效拟配的主要方法,应用较广泛,但由于实际高阶系统的频域响应数据较难获取,对该方法的使用造成了限制[2]。
飞机的时域响应数据易获得,并考虑了高频、非线性等各种因素的影响,且适用于不同的飞机设计阶段。因此,对基于时域数据的低阶等效拟配方法进行研究和探讨。
1 时域数据的获取
根据飞机设计阶段的不同,时域数据的来源分为两类:飞行仿真数据和飞行试验数据。在获得大量有效的试飞数据之前,时域输入数据的获得只能是飞行仿真数据。飞行仿真数据具有不同的设计阶段适应性,既可以由模拟器试验或六自由度飞行仿真得到,亦可以由解耦后的纵向或横航向运动方程求取。现阶段缩比验证飞行技术的快速发展,提供了时域数据的又一重要来源。转入试飞阶段后,飞行试验数据体现了飞机的最真实的飞行动力学特性,应是时域数据的最主要来源。
1.1 飞行仿真数据
飞行仿真数据由解算飞行动力学方程得出。飞机六自由度飞行动力学方程如下[3]:
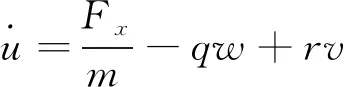
(1)
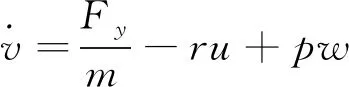
(2)
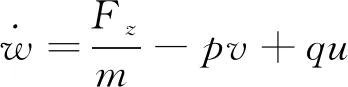
(3)
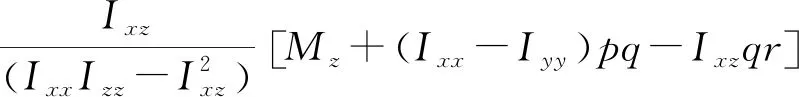
(4)
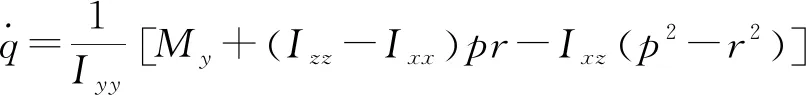
(5)

(6)
式中,(FX,Fy,Fz),(MX,My,Mz)分别为作用在飞机上的力和力矩在体轴系中的三分量; (u,v,w),(p,q,r)分别为飞机的线速度和角速度在体轴系中的三分量;m为飞机质量,Ixx,Iyy,Izz,Ixz为相应的惯性矩和惯性积。
上述微分方程组无解析解,须采用数值方法求解。给定飞行状态初值和操纵输入,即可用龙格-库塔法或线性多步长法进行计算。
1.2 飞行试验数据
和飞行仿真数据不同,飞行试验数据会引入过程噪声和测量噪声等,需对飞行试验数据进行数据平滑处理,但切不可平滑过度,否则会湮没数据中的有用信息。
此外,在飞机的纵向短周期双拟配过程中要用到过载数据。当过载传感器安装位置不在飞机重心处时,需要对过载传感器测量数据进行修正,修正公式如下[4]:

(7)
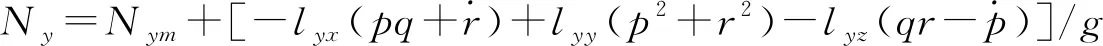
(8)
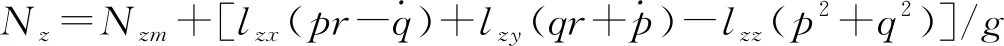
(9)
式中,下标m表示飞行测试数据,(lxx,lxy,lxz)、(lyx,lyy,lyz)、(lzx,lzy,lzz)分别为过载传感器Nx、Ny、Nz安装位置在体轴系中的三分量。
2 等效拟配法
一个高阶系统的低阶等效系统是指,两个系统在相同初始条件下,受同样外界激励作用(杆力/杆位移输入)下,在一定的频域范围或时间区间内,相应输出值的差值在某个指标意义下达到最小,则称低阶系统是满足某些条件的高阶系统的低阶等效系统[5]。
基于时域数据的等效拟配法有两种途径:一种是将时域数据通过傅里叶变换得到相应的频域数据,继而在频域里进行等效拟配,本文称为频域等效拟配法,另外一种方法是将时域数据直接进行拟配,得出相应的频域指标,称之为时域等效拟配法。二者最大的区别在于拟配指标函数的不同,前者指标函数为频域响应参数的组合,如幅值误差和相角误差等,后者则与高阶系统和低阶等效系统时域响应之差直接相关。
2.1 等效系统模型
对于经典飞机的纵向运动,运动响应包括短周期模态和长周期模态。考虑到高阶系统高频模态所体现的相位延迟,在等效模型中加入一时间延迟项。得到基本的等效系统数学模型如下:

(10)

(11)
式中,q,nz分别为俯仰角速度和法向过载;δes,Fes分别为升降舵偏度和杆力;Tθ1,Tθ2,Tn1则为等效分子时间常数,ωsp,ζsp,ωp,ζp为等效短周期及长周期的自然频率和阻尼比;K,τ分别为增益和等效时间延迟。
根据实际飞机的响应,若对上述基本模型进行适当的改变,则可得到更好的拟配结果。如若飞机的时域响应中未充分激发出长周期模态,或者飞机的长短周期模态可明显分开时,可对驾驶员最为关心的短周期模态单独进行拟配,拟配模型变为

(12)

(13)
2.2 频域等效拟配法
该方法首先需将时域数据转换得到频域数据,然后在频域里进行等效拟配。任何一个时域信号都可以表示成包含众多频率的正弦信号之和。通过快速傅里叶变换(FFT)可从时域响应中提取出频域响应数据,具体算法见文献[6]。
在得到飞机的频响数据后,构造出拟配指标函数:
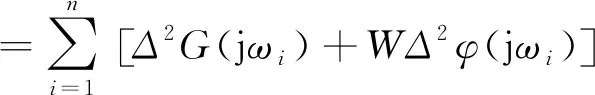
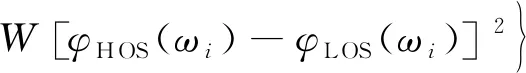
(14)
式中,GHOS,φHOS,GLOS,φLOS,分别为高阶系统和低阶等效系统的频率响应的幅值和相角;ωi为第i个拟配频率;W为加权因子,取为0.017 45,表示1dB的幅值误差与7°的相角误差在拟配指标函数中具有相同的贡献量。
2.3 时域等效拟配法
时域等效拟配法是在一定的时间区间内,低阶等效系统和高阶系统的响应输出值的差值在某个指标意义下达到最小。时域等效拟配法的拟配指标函数为

(15)
式中,N为时域响应离散点的个数;t1,tN分别为起始时刻和终止时刻,yHOS,yLOS则分别为高阶系统和低阶等效系统时域响应输出。
2.4 优化算法
当等效拟配的指标函数确定以后,等效拟配问题就转变为寻优问题。常用的迭代优化算法包括单纯形算法(SIMPLEX算法)、牛顿-拉夫逊算法、梯度法等。本文采用牛顿-拉夫逊算法,并使用飞机的理论计算值作为迭代初值,以弥补牛顿-拉夫逊算法对初值较敏感的不足。
3 算例和分析
以某型飞机为例,建立了其六自由度飞行仿真模型。纵向操纵输入信号分别为“3211”输入和“11”输入,分别见图1和图2,以研究不同输入对等效拟配结果的影响。

图1 纵向操纵输入,“3211”

图2 纵向操纵输入,“11”
将两种操纵输入下的时域响应数据分别采用频域等效拟配法和时域等效拟配法进行等效拟配。该型飞机纵向长周期和短周期模态差异较大,故可将其分开,低阶等效系统模型采用式(12)和式(13)所示模型。低阶等效模型的时域仿真结果和高阶系统的时域仿真结果的重合度是检验拟配结果是否合理的重要依据。只有二者吻合的很好,才能说明拟配结果是合理可信的。图3给出了一示例,拟配条件为“3211”输入、频域等效拟配法。

图3 低阶等效系统和高级系统时间历程曲线
飞机短周期模态特性理论值由两种方法计算,一是通过纵向小扰动运动方程,求其状态矩阵的特征值得到;二是通过六自由度全量运动方程线化计算得到,具体求解见文献[7]。
某型飞机典型巡航状态的纵向短周期模态特性理论计算结果和等效拟配结果对比见表1。
由表1可见,采用纵向解耦的小扰动运动法和六自由度线化方法所得的理论计算结果,自然频率和阻尼比都十分接近。总的来看,两种输入信号下的频域等效拟配法和时域等效拟配法的拟配结果和理论计算结果都相吻合,尤其是“3211”输入下的频域等效拟配法结果,不管是自然频率还是阻尼比,都和理论计算值十分接近。
不同操纵输入激发出飞机的不同运动模态,使得时域响应数据所含待辨识模态的信息量也就不同。对该算例飞机,其短周期频域约为2 rad/s,“3211”输入信号较“11”输入信号,其功率频谱在2 rad/s附近具有更大的能量,故其输出信号含有更多的短周期模态信息,辨识结果和理论计算值更为接近。

表1 短周期模态等效拟配结果和理论计算结果对比
4 结论
基于时域数据,提出了两种低阶等效拟配方法。时域数据既可以是飞行仿真数据,亦可以是飞行试验数据,但对飞行试验数据需对关键参数的测量值进行修正。
对基于时域数据的等效拟配法提出了两种实现途径:频域等效拟配法和时域等效拟配法。使用算例飞机不同操纵输入信号下仿真数据进行了两种方法的低阶等效系统拟配。通过低阶等效系统拟配结果和理论计算结果对比、以及低阶等效系统和高阶系统的仿真结果对比等,表明等效拟配结果合理可信。为获得含有更多信息的时域数据,操纵输入应在所关心的模态频率附近拥有足够的能量以充分激起这些模态的运动。

