渡槽整体结构环境激励模态试验
顾培英,刘冬梅,邓 昌,汤 雷
(1.南京水利科学研究院材料结构研究所,江苏 南京 210029;2.水利部水科学与水工程重点实验室,江苏 南京 210029;3.南京科技职业学院,江苏 南京 210048)
结构损伤诊断及安全评价一直是工程界关注的重点,笔者对大体积混凝土结构整体安全评价进行了某些尝试[1-5],但国内外对渡槽结构安全评价研究较少,为此提出基于振动诊断技术的大跨高架渡槽结构安全评价技术,并用其对渡槽结构典型破坏特征进行了较为全面的研究[6-9]。根据模态参数(包括模态频率、振型、阻尼)分析结果,评价渡槽整体结构安全状况,该方法在其他工程领域已广泛应用。模态试验分析是获得结构动力特性的主要手段。模态试验分析方法已有40 a的发展历史,渡槽动力特性数值模拟研究较多,但针对渡槽结构的模态试验研究较少,笔者分别对渡槽排架结构人工激励[10]、环境激励[11]模态试验分析开展了研究,提出排架结构模态试验选择单向SIMO(single input multiple output)法优于双向MIMO(multiple input multiple output)法的结论。
实际大型结构往往在风力、水流、交通等自然力或工作状态下能激励出识别模态参数的振动响应,无需且往往现场也无法施加人工激励。根据有限元模态分析及人工激励模态试验结果,渡槽结构多向模态振型基本为横竖双向,无明显纵横竖三向模态振型,所以环境激励多向模态试验只考虑横竖双向[10]。试验还表明,纵向模态频率较低、阶数较少,无水、有水工况识别结果基本相似;横向、竖向、横竖双向模态随水位增加,大多数模态振型基本相似,存在个别模态丢失情况。所以本文针对无水工况,首先分别对纵向、横向、竖向进行SIMO法单向环境激励模态试验,再用MIMO法同时测试横竖双向响应;选用增强频域分解法(enhance frequency domain decomposition,EFDD)分别识别纵向、横向、竖向、横竖双向模态参数,重点分析模态频率、模态振型及其相关MAC(modal assurance criterion)矩阵校验;综合分析单、双向识别结果,比较模态参数识别精度,提出渡槽结构环境激励模态试验方法。
模态试验分析方法有频域分解法、时域分解法[10,12]。频域分解(frequency domain decomposition,FDD)法是一类运行模态分析(operational modal analysis,OMA)方法,通过测量结构环境激励下的振动响应,得到反映真实动力特性的模态参数[13],该方法由峰值拾取法发展而来[14]。FDD 法最早由 Brincker 等在复模态指示函数基础上提出,在满足白噪声激励假设和小阻尼假设时,识别模态频率和模态振型[13]。Brincker等随后提出了增强频域分解法(EFDD),将经奇异值分解后的单自由度功率谱进行傅里叶逆变换,得到对应的自相关函数,从而通过对数衰减法获得模态频率和阻尼比[11,14-15]。
频域分解法核心是对响应功率谱进行奇异值分解,将功率谱分解为对应多阶模态的单自由度系统功率谱。该方法识别精度较高,抗干扰能力较强。但3个假设必须同时满足:(a)激励为白噪声;(b)结构阻尼为小阻尼;(c)当有密集模态时,必须正交。
1 试 验 方 案
根据新疆某渡槽,主要构件按1∶15几何比尺制作一跨简支梁式小型排架渡槽结构,模型采用钢筋砂浆结构[10]。排架柱与上部支撑横梁整体固接浇筑,槽身单独浇筑,槽身与横梁通过橡胶支座连接,橡胶支座用结构胶分别与槽身、横梁粘接。搅拌机搅拌砂浆,排架柱与横梁、槽身分别采用有机玻璃、木模浇筑成型。主筋选用∅8 mm带肋钢筋,立柱箍筋为外径80 mm、粗5 mm的铁环。排架柱采用3根直径120 mm、高1 500 mm的立柱,立柱净间距280 mm,每根立柱4根纵向钢筋,纵向钢筋底部与底座钢板固定,顶部与支撑梁钢筋绑扎,底座钢板用膨胀螺栓与地面固定,立柱箍筋间距300 mm。横梁尺寸1 000 mm×200 mm×100 mm,上部由3根纵向钢筋、5根间距约200 mm横向钢筋组成单层钢筋网,并与立柱钢筋绑扎。槽身长2 000 mm,为2孔矩形断面,单孔净宽370 mm,净高240 mm,底板厚40 mm,中墙厚40 mm,两侧墙厚60 mm,中墙及侧墙底部布置纵向底座,中墙底座尺寸130 mm×20 mm,侧墙底座尺寸80 mm×20 mm。采用单层钢筋网布置,底板、每个侧墙、中墙分别布置8根、3根、4根纵向钢筋,横向钢筋间隔200 mm。
环境激励模态试验装置一般包括传感及信号放大设备、信号采集设备、信号分析系统。选用CA-YD-107加速度传感器、INV-8 多功能抗混滤波放大器、INV306U-6260智能信号采集处理分析仪、DASP智能数据采集和信号分析系统。布置130个测点,测点4为参考点,分多组测试,测点位置编号如图1所示。对于该小型渡槽结构,由于模态频率较高,室内试验环境安静,仍需借助锤击模拟环境激励,尽量避开模态节点,在测点1激励,但不需测试激励信号,分析方法同典型环境激励方法。

图1 测点位置编号Fig.1 Point number of measuring points
2 模态试验结果及分析
2.1 纵向模态识别结果及分析
环境激励下纵向模态响应功率谱奇异值曲线如图2所示,尽量在峰值处收取模态主峰,收取了3阶模态,渡槽结构纵向模态谱峰明显。纵向前3阶模态频率分别为9.616 Hz、16.896 Hz、100.732 Hz。

图2 环境激励下纵向模态响应功率谱奇异值曲线Fig.2 Singular value curve of response power spectrum of longitudinal modes under ambient excitation
采用模态振型相关MAC矩阵非对角线元素平均值、最大值为评价指标,二数值越小越好。Carne提出,工程上非对角线元素一般小于0.25可近似认为模态正交[10,16-17],0.25作为阈值普遍应用于传感器优化布置研究中。本文将0.25作为两模态正交性好坏的阈值。
3个非对角线元素中MAC0102、MAC0203(01、02分别代表1阶、2阶模态,其余类推)分别为0.159 6、0.041 6,小于0.25,MAC0103为0.310 5,略大于0.25,整体上模态振型正交性较好,模态识别精度较高。
环境激励下纵向前3阶模态振型如图3所示。由图3可知,除第2阶个别点拟合较差外,其他识别效果均较好。模态以排架结构振动为主,槽身整体平动或转动或不动。
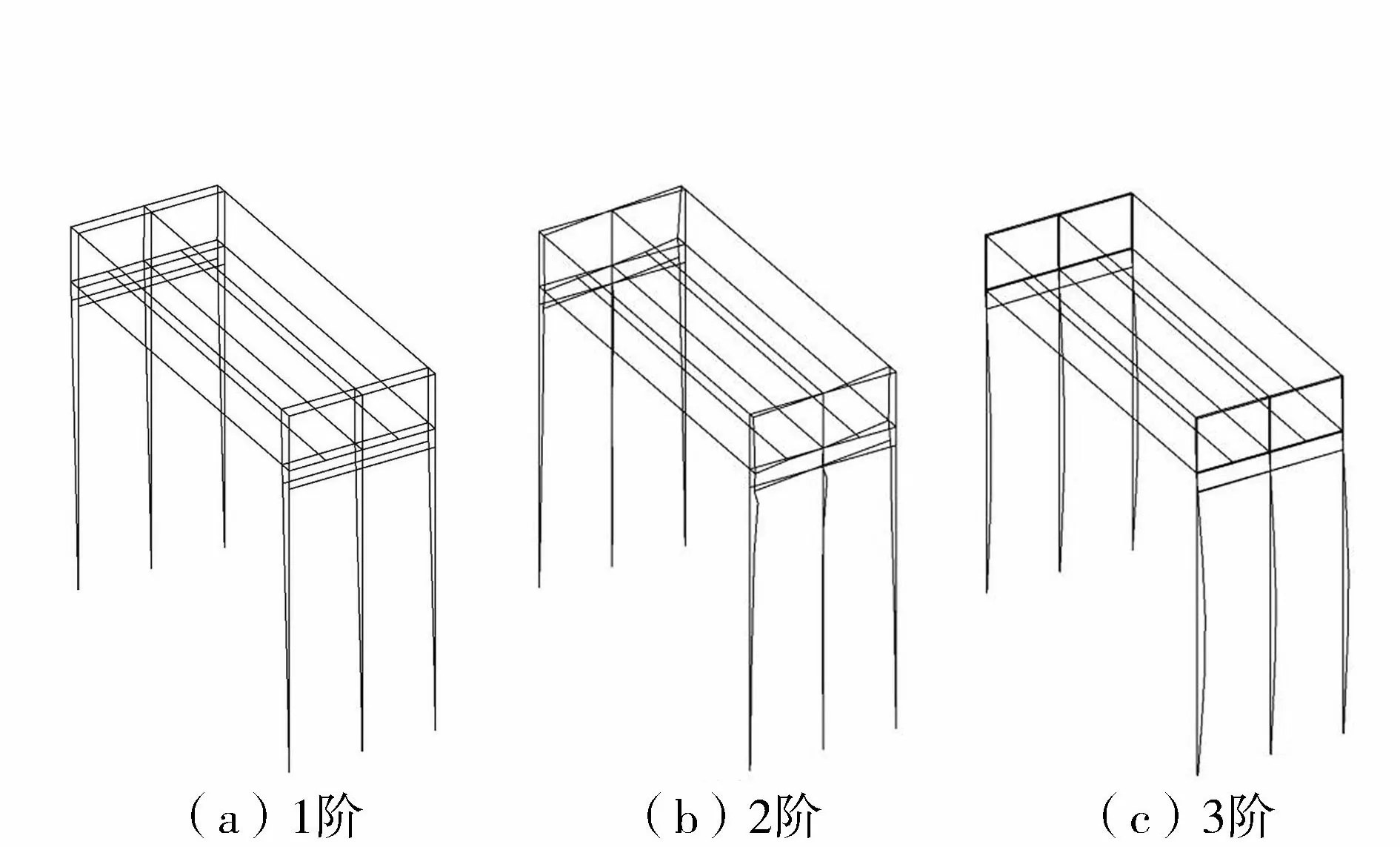
图3 环境激励下纵向前3阶模态振型Fig.3 First three order modal shapes of longitudinal modes under ambient excitation
纵向前3阶模态阻尼比分别为2.464%、1.448%、2.162%,在正常范围内[10,11,18-20]。
2.2 横向模态识别结果及分析
环境激励下横向模态响应功率谱奇异值曲线如图4所示,收取了11阶模态,其中8阶谱峰明显或较明显、3阶较小,大多数谱峰明显或较明显。

图4 环境激励下横向模态响应功率谱奇异值曲线Fig.4 Singular value curve of response power spectrum of transverse modes under ambient excitation
环境激励下横向模态振型相关MAC矩阵校验如图5所示。MAC矩阵大多数非对角线元素较小,80.0%的非对角线元素小于0.25,平均0.165 9,大多数模态振型正交性较好,模态识别精度较高。MAC0203、MAC0306、MAC0408、MAC0809、MAC1011略大于0.25,识别效果尚可;MAC0509最大,为0.787 9;MAC0103、MAC0308、MAC0608、MAC0810、MAC0910次之,分别为0.559 0、0.393 4、0.358 3、0.391 1、0.423 5。说明第5阶与第9阶模态正交性较差,第1阶与第3阶、第3阶与第8阶、第6阶与第8阶、第8阶与第10阶、第9阶与第10阶次之。
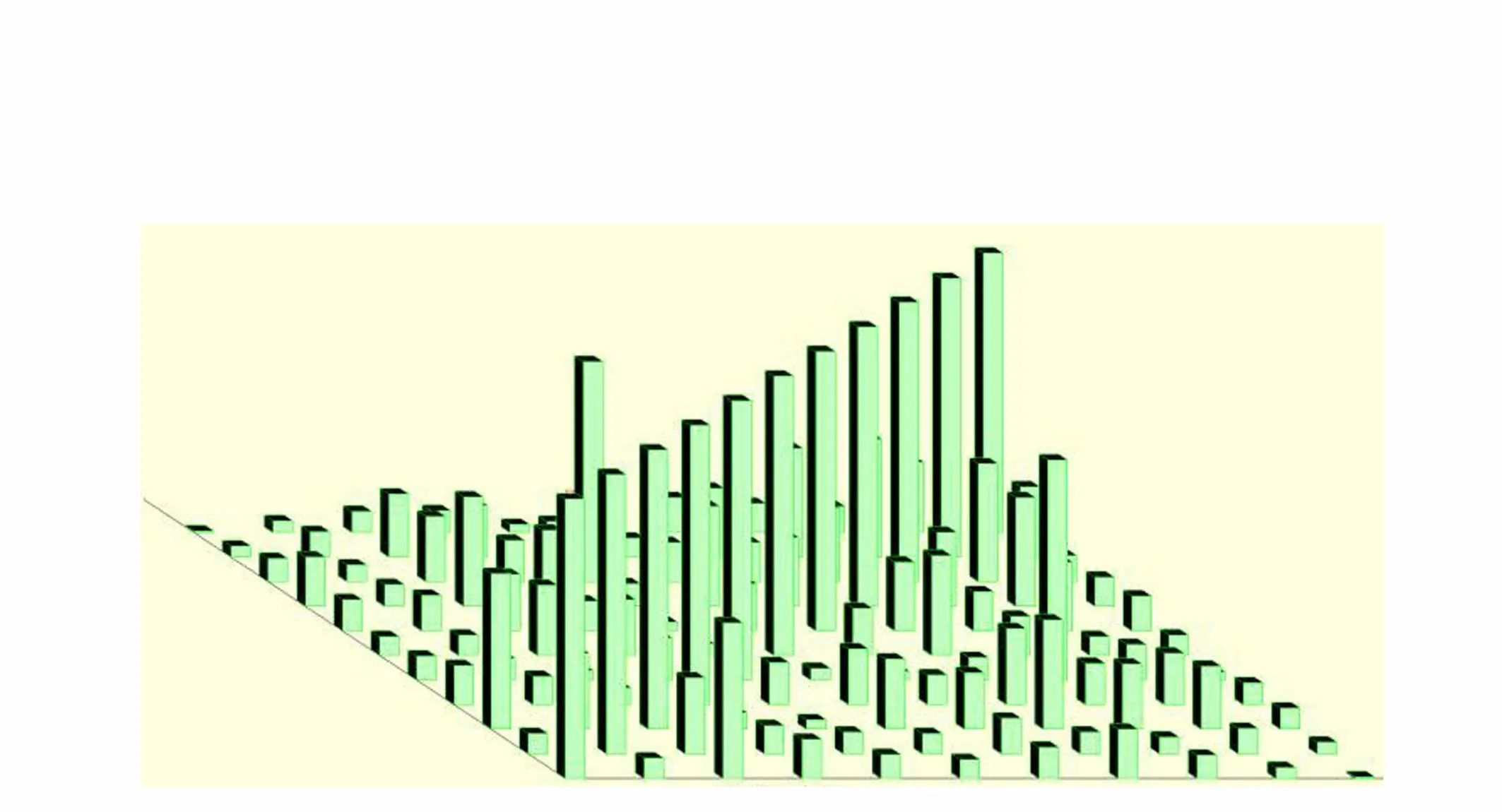
图5 环境激励下横向模态振型相关MAC矩阵校验Fig.5 Modal correlation MAC matrix calibration of transverse modes under ambient excitation
环境激励下横向模态参数识别结果见表1,前11阶模态振型图如图6所示。根据模态振型图可知,除第3阶、4阶、6阶、9阶模态振型尚可、较差或稍差外,大多数模态识别效果较好。前4阶模态以排架结构振动为主,槽身整体平动或转动或横摇(纵向跨中振幅大),第5阶模态之后(包括第5阶),绝大多数以槽身振动为主,排架几乎不动或振动幅度较小。由表1可知,模态阻尼比为0.901%~2.289%,平均值1.535%,横向模态阻尼在正常范围内。
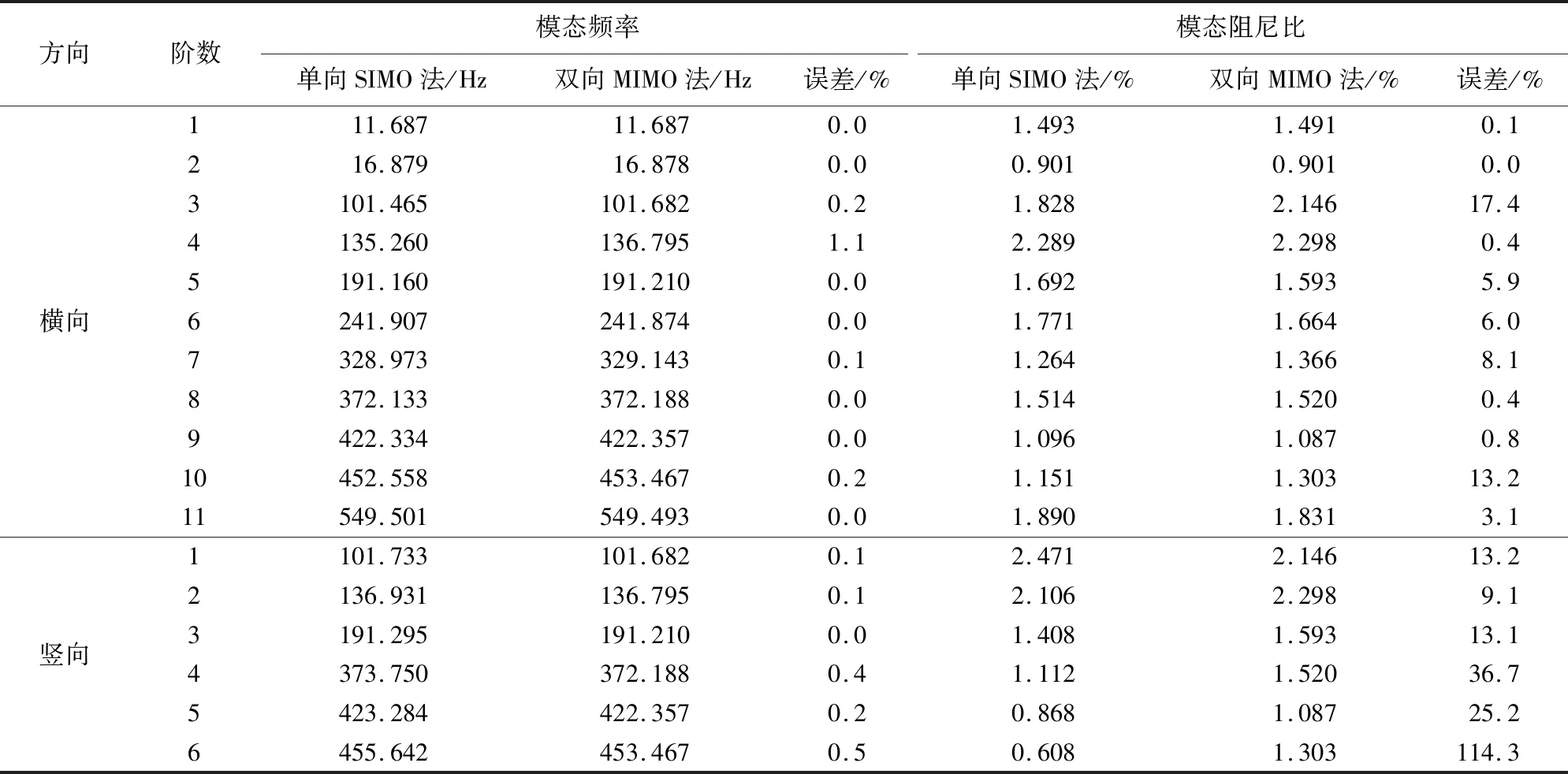
表1 环境激励下模态参数识别结果汇总及比较Table 1 Result summary and comparison of identified modal parameters under ambient excitation

图6 环境激励下横向前11阶模态振型Fig.6 First 11 order modal shapes of transverse modes under ambient excitation
2.3 竖向模态识别结果及分析
根据环境激励下竖向模态响应功率谱奇异值曲线(图略),收取了6阶模态,其中4阶谱峰明显、2阶很小,大多数谱峰明显。
模态振型相关MAC矩阵(图略)非对角线元素稍大,只有60.0%非对角线元素小于0.25,平均0.280 8,即只有60.0%模态振型正交性较好。MAC0104、MAC0106略大于0.25,识别效果尚可;MAC0102最大,为0.761 4;MAC0305、MAC0405、MAC0506次之,分别为0.370 6、0.422 4、0.562 5。说明第1阶、第2阶模态正交性较差,第3阶与第5阶、第4阶与第5阶、第5阶与第6阶次之。
环境激励下竖向模态参数识别结果见表1,前6阶模态振型图如图7所示。根据模态振型图,前3阶模态振型识别效果较好,第4~6阶模态振型尚可。竖向模态以槽身振动为主。由表1可知,模态阻尼比为0.608%~2.471%,平均值1.429%,阻尼比在正常范围内。
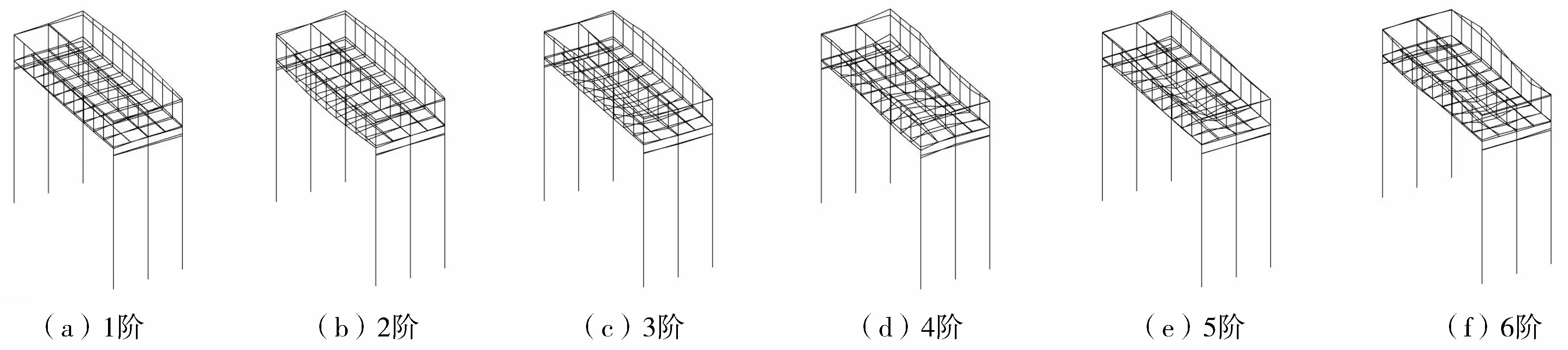
图7 环境激励下竖向前6阶模态振型Fig.7 First six order modal shapes of vertical modes under ambient excitation
2.4 横竖双向模态识别结果及分析
环境激励下横竖双向模态响应功率谱奇异值曲线如图8所示,收取了11阶模态,其中8阶谱峰明显或较明显、3阶较小,大多数谱峰明显或较明显。

图8 环境激励下横竖双向模态响应功率谱奇异值曲线Fig.8 Singular value curve of response power spectrum of bidirectional modes under ambient excitation
模态振型相关MAC矩阵大多数非对角线元素较小,87.3%非对角线元素小于0.25,平均0.131 4,大多数模态振型正交性较好,模态识别精度较高。MAC0103、MAC0809、MAC1011略大于0.25,识别效果尚可;MAC0304最大,为0.463 7;MAC0509、MAC0810、MAC0910次之,分别为0.432 6、0.325 2、0.442 2。说明第3阶与第4阶模态正交性较差,第5阶与第9阶、第8阶与第10阶、第9阶与第10阶次之。
环境激励下横竖双向模态参数识别结果见表1,前11阶模态振型如图9所示。由图9可知,除第3阶、4阶、6阶、9阶模态振型尚可、较差或稍差外,大多数模态识别效果较好。前4阶模态以排架结构振动为主,槽身整体平动或转动或横摇(纵向跨中振幅大),第5阶模态之后(包括第5阶),绝大多数以槽身振动为主,排架几乎不动或很小。由表1可知,模态阻尼比为0.901%~2.298%,平均值1.564%,在正常范围内。
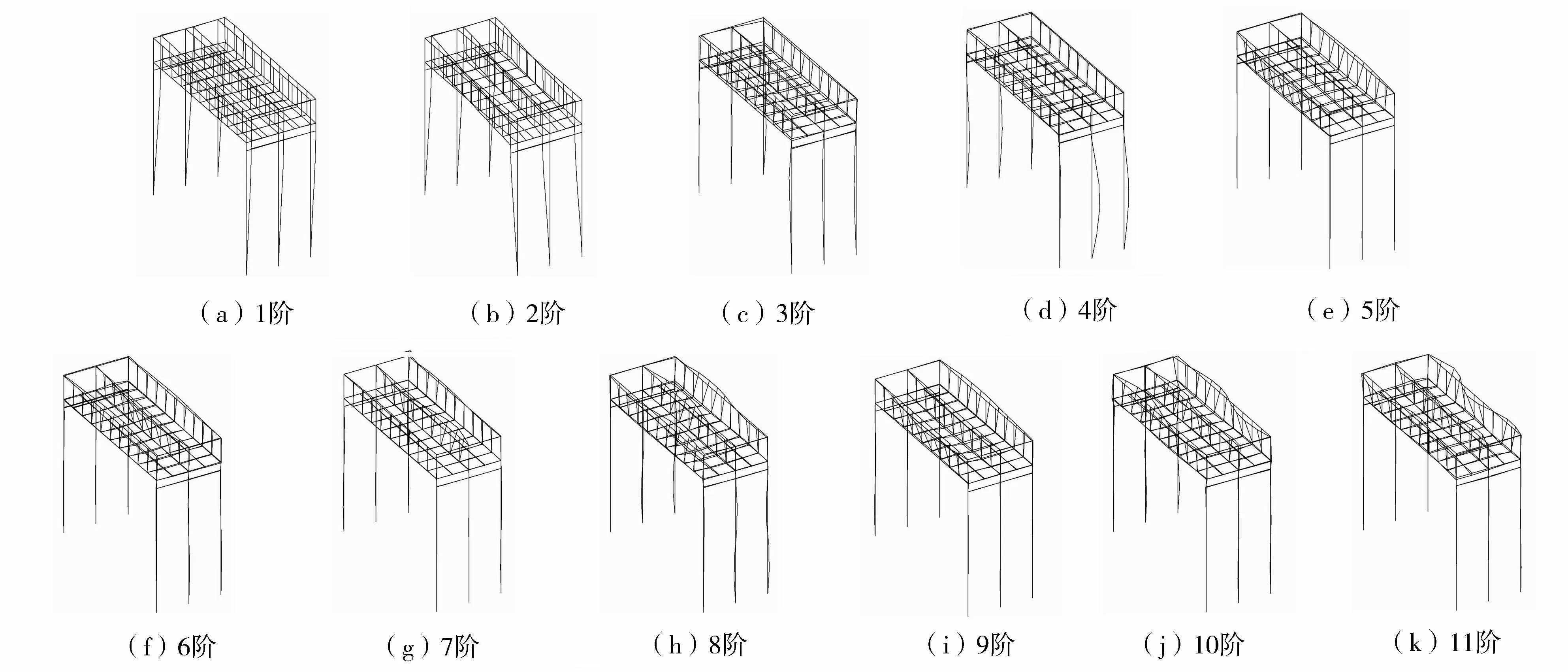
图9 环境激励下横竖双向前11阶模态振型Fig.9 First 11 order modal shapes of bidirectional modes under ambient excitation
2.5 横竖双向与单向模态识别结果比较分析
综合前面分析结果,横竖双向MIMO法识别出的模态规律与横向SIMO法相似。模态振型图显示,单向SIMO法识别出的横向、竖向模态分别为横竖双向MIMO法的槽身横向、竖向分量。所以,渡槽结构横竖双向MIMO法识别出的槽身模态信息更为全面。
为进一步比较单向SIMO法、双向MIMO法模态识别结果,环境激励下模态参数识别结果汇总及比较列于表1。根据表1,环境激励下单向SIMO法与双向MIMO法模态频率相差很小,平均误差0.2%,最大误差1.1%。但模态阻尼比误差较大,尤其是竖向。横向模态阻尼比平均误差5.0%,最大误差17.4%。竖向第6阶阻尼比误差高达114.3%,其他阶阻尼比平均误差19.5%。一般情况下模态阻尼识别精度较低,离散性大[7-8],本次环境激励获得的大多数模态阻尼比在正常范围,误差可接受。
渡槽结构由于横竖双向MIMO法识别出的槽身模态信息全面,同时包含了横向、竖向模态分量。从槽身模态识别准确性、信息全面性而言,渡槽结构环境激励模态试验选择双向MIMO法优于单向SIMO法。
3 结论与展望
a.采用2种方法识别出的模态功率谱奇异值曲线大多数谱峰明显或较明显,大多数模态识别效果较好。
b.纵向模态以排架结构振动为主,槽身整体平动或转动或不动。
c.前4阶横向模态以排架结构振动为主,槽身整体平动或转动或横摇(纵向跨中振幅大),第5阶模态之后(包括第5阶),绝大多数以槽身振动为主,排架几乎不动或振动幅度很小。
d.竖向模态以槽身振动为主。
e.横竖双向MIMO法识别出的模态规律与横向SIMO法结果相似。单向SIMO法识别出的横向、竖向模态分别为横竖双向MIMO法识别出的槽身横向、竖向分量。
f.环境激励下单向SIMO法与双向MIMO法识别出的模态频率误差较小,模态阻尼误差较大,但仍在正常范围内。由于横竖双向MIMO法识别出的槽身模态信息全面,同时包含了横向、竖向模态分量。从模态识别准确性、信息全面性而言,渡槽整体结构环境激励模态试验选择双向MIMO法优于单向SIMO法。
需要指出的是,本文研究只是渡槽结构整体安全评价的基础,下一步即将开展损伤状态下渡槽模态参数变化规律研究。以上研究成果可推广应用于排架类整体结构工程的模态参数识别中。

