基于矩阵分解的降水时空插值方法
陈 华,盛 晟,夏润亮,马 瑞,朱跃龙,李 涛
(1.武汉大学水资源与水电工程科学国家重点实验室,湖北 武汉 430072;2.黄河水利委员会黄河水利科学研究院,河南 郑州 450003;3.长江空间信息技术工程有限公司,湖北 武汉 430010;4.河海大学计算机与信息学院,江苏 南京 210098)
降水数据在国家防汛、抗旱等自然灾害应急决策管理中具有重要的作用,精确的雨量估算和空间分布确定能为自然灾害的应急决策提供科学准确的数据[1],提升应急管理水平,社会效益显著。雨量站网是目前最主要的降水观测和采集系统,其主要特点是便捷、实时和准确;但由于站点是离散的,需要借助于空间插值方法来得到降水的空间连续分布。
现有的降水空间插值方法,不论是整体插值(如边界内差法、趋势面分析法)还是局部插值(如克里金法[2-3]、泰森多边形法[4]、反距离权重法[5]),都是基于插值点与雨量站的地理位置关系,利用插值的当前时刻降水信息进行插补。这些方法主要是基于“地理学第一定律”[6]的基本假设:空间位置上越靠近的点,具有相似特征值的可能性越大;而距离越远的点具有相似特征值的可能性越小。这些方法都仅仅考虑了空间上的关系,没有考虑降水序列的过去临近信息对当前值的影响,无法将历史降水信息应用于当前时刻降水判断和未来趋势预测。也有不少学者开展了降水时空插值方法研究,比如STARMA和具有时间扩展模块的克里金插值方法[7-9]。现有的结果都表明,考虑时间维度的插值方法精度都比只考虑空间维度的插值方法精度高,但由于算法过于复杂,并没有被广泛推广应用。
为了充分利用降水的时间序列和空间信息以提高降水空间分布及雨量估算的精度,本文引进了推荐系统中的矩阵分解方法,来实现降水数据的时空插值,并对降水空间插值结果进行了评价。
1 插 值 方 法
1.1 Funk-SVD模型
矩阵分解是解决协作过滤问题最常用的方法之一,其将用户的商品偏好程度看作用户-商品评分矩阵,并使用已知用户对商品的评分来预测用户在商品选择中的偏好并进行推荐[10-11]。由于具有较高的预测准确度,矩阵分解已成为环境科学、生物医学等许多领域常用的插值方法[12-14]。González-Macías等[15]使用正矩阵分解法来识别和确定海底沉积物中人为重金属的来源;Lee等[16]将非负矩阵分解法应用于基因数据的表达,量化了不同剂量的pan-PPAR兴奋剂在小鼠体内引起的分子变化。Funk-SVD模型是Funk[17]提出的一种矩阵分解的变体模型,其基本思想是用户和商品可以分别由从用户-商品评分矩阵推断出的潜在特征向量来描述,由用户和项目特征之间的高度对应性形成预测和推荐[18],这种模型也称作隐语义模型。
基于Funk-SVD模型的降水时空插值模型结构如图1所示。空间上不同点在多个时刻的降水数据可以看作是一个内在相关的矩阵P=(Pij),其中列代表时间,行代表空间。无降水记录的点在矩阵P中对应位置为空值,即为待插值点。为了得到该位置的值,可以根据已有的降水记录对矩阵P进行分解,通过分解后两个矩阵的乘积来补全原矩阵P中空缺位置的值。
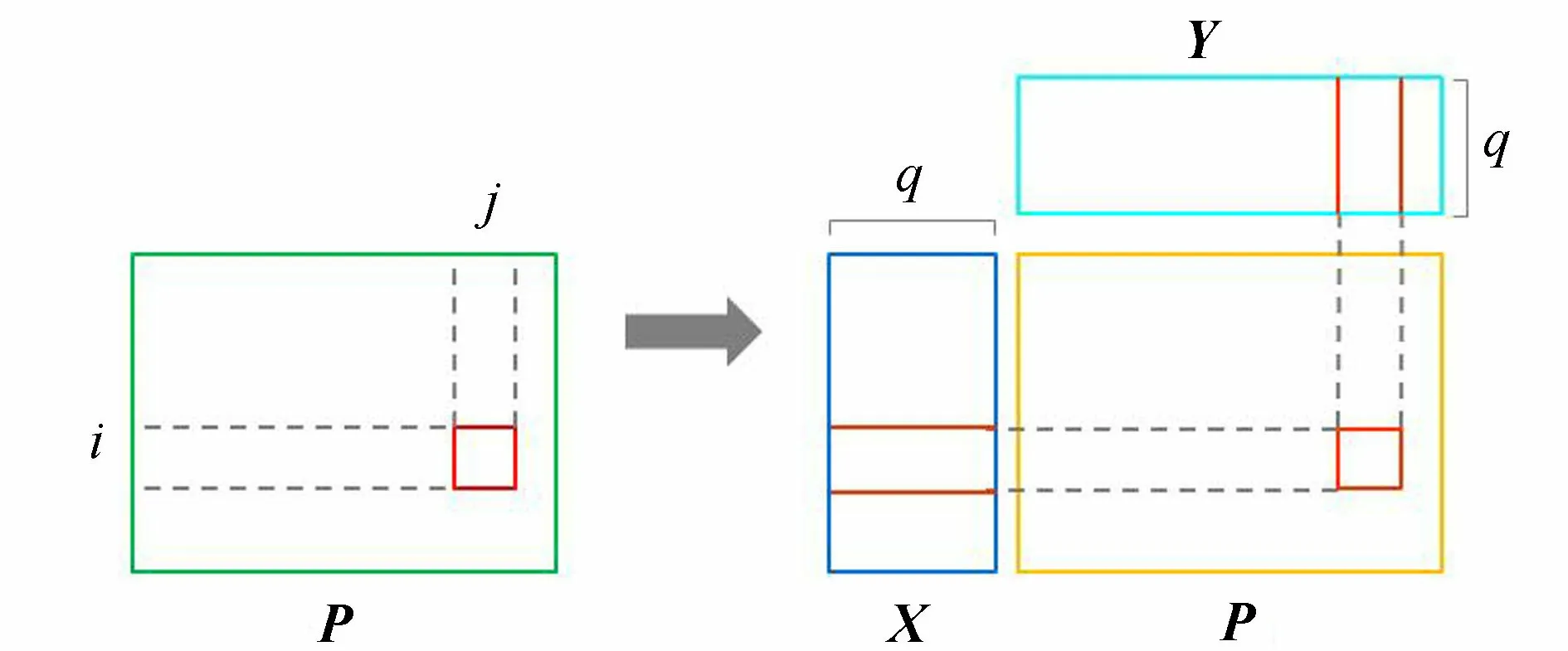
图1 基于Funk-SVD模型的降水时空插值方法结构示意图Fig.1 Structure diagram of spatiotemporal interpolation method of rainfall based on Funk-SVD model
具体来说,降水数据矩阵的时间和空间之间存在隐式关系,无法直接求解,所以需要潜在因子来建立间接关系。假设存在影响降水的q个潜在因子,从图1可以看出,该矩阵P可以分解为空间特征矩阵X和时间特征矩阵Y,分别包含m个q维行向量X1、X2、…、Xm和n个q维列向量Y1、Y2、…、Yn,其中Xi(i=1,2,…,m)代表i站点q个潜在因子的影响程度,其包含的特征数据越相近,潜在因子对降水的影响效果越相近;Yj(j=1,2,…,n)描述j时刻潜在因子的关联关系,相关程度越高,对应的特征值越大。因此,可以基于潜在因子的影响程度和关联关系计算某时某地的降水量。也就是说,Pij可以由Xi和Yj相乘得到,其计算公式如下:
(1)
1.2 插值方法计算流程
基于Funk-SVD模型的降水时空插值方法具体计算流程如图2所示。图2涉及的主要有4个计算步骤:
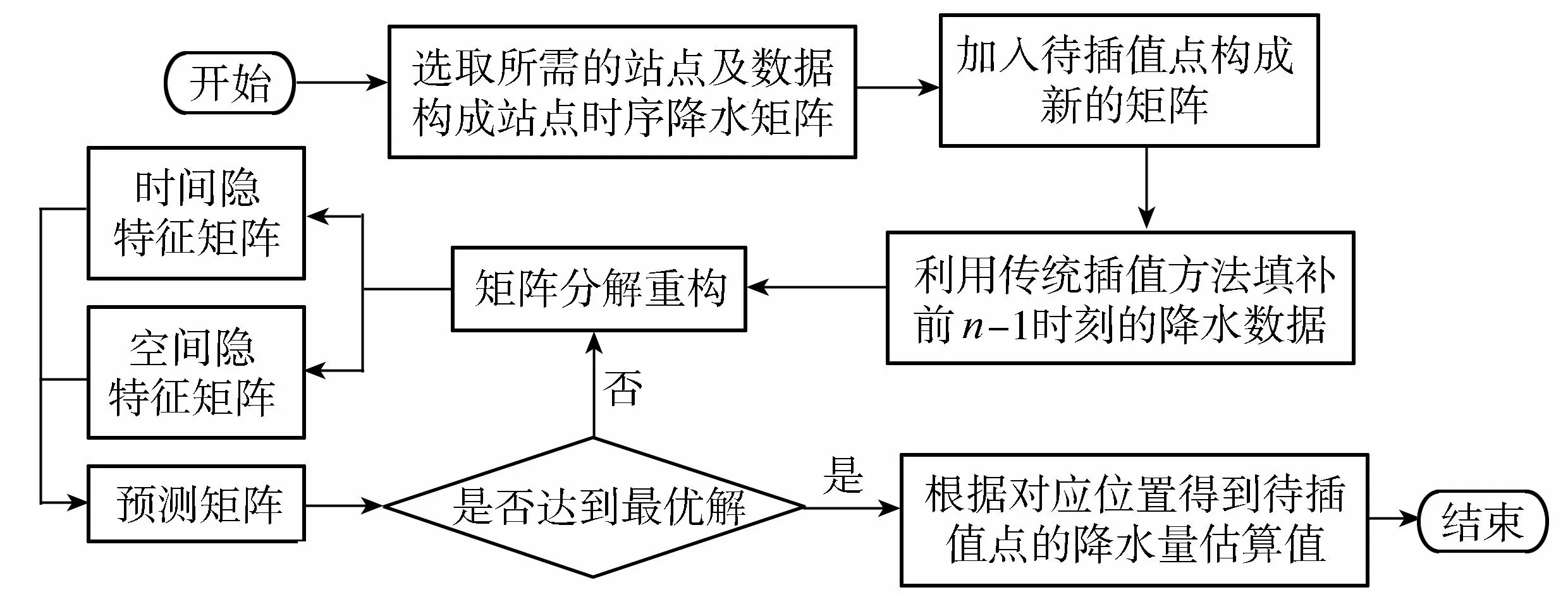
图2 基于Funk-SVD模型的降水时空插值方法计算流程Fig.2 Calculation flowchart of spatiotemporal interpolation method of rainfall based on Funk-SVD model
a.对于j时刻在流域上的某点I,可以确定一个由m个站点和n个时刻组成的降水数据矩阵。所涉及的m个站点是在计算所有可能排列组合后由空间均匀度L选出的最优集合,空间均匀度是点集的空间关系度量,其值越大,点分布越均匀,计算公式为
(2)
式中:A——涵盖所有站点的矩形网格面积;a——独占圆面积的总和,某点的独占圆的定义为以该点为圆心,与最近点距离的一半为半径的圆。考虑到矩阵分解的效率和精度,时刻数n的取值如下:
(3)
式中:t0——降水事件的开始时刻;N——前期影响时刻总数阈值。如果降水持续时间不长,n个时刻就从降水开始时刻t0开始取到插值时刻j。如果降水持续时间长,对于距开始时间超过N个时刻的插值时刻来说,n个时刻就取j时刻以及前N个时刻。
b.增加一行代表流域上一点I,得到一个新矩阵R。矩阵第m+1行前n-1个值为已知的j时刻前的降水,由传统插值方法计算得到。第n个值为空,代表待插值点。
c.利用Funk-SVD模型将矩阵R分解成时间特征矩阵X和空间特征矩阵Y。Funk-SVD模型通过最小化所有已知点的预测值平方误差来计算时间和空间的潜在特征。此外,为了防止出现过度拟合的情况,将正则化方法引入目标函数:
(4)


(5)
(6)
式中:α——机器学习的学习率。
d.将优化得到的时空特征矩阵相乘,可以得到一个无限逼近于原矩阵的重构矩阵R′,且R′中每个位置都有值。原始矩阵R和重构矩阵R′中各元素为一一对应的关系,重构矩阵R′第m+1行第n列的值即为点I在j时刻的降水量。
1.3 评价指标
使用交叉验证的方法进行插值的精度验证,即每次将一个站点看作未知点,利用其余所有站点进行插值,将结果和观测值进行比较。采用均方根误差(RMSE)、平均绝对误差(MAE)、百分误差(PERC)和双样本Kolmogorov-Smirnov检验的概率值(KS)[19-20]等4个评价指标来验证插值精度,采用反距离权重法和普通克里金法这两种广泛应用的空间插值方法与Funk-SVD模型结合进行插值。这两种方法都是基于站点的观测值和权重来得到待插值点的计算值,计算公式如下:
(7)
式中:Z——待插值点的计算值;Zi——站点的观测值;wi——站点的权重,其中IDW和OK两种方法计算站点权重的公式分别为
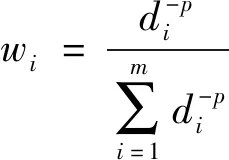
(8)
(9)
式中:di——站点到目标点的距离;p——距离的幂;μ——拉格朗日乘子;γ——空间上两点间的半变异函数;xi、xh——插值利用到的站点;x——待插值点。
2 实 例 验 证
2.1 研究区域及数据
选择黄河流域的小浪底到花园口区间为研究区域,该区域位于黄河下游(东经109°42′~113°54′、北纬33°17′~37°30′),是黄河流域主要暴雨来源区之一,暴雨来势急、汇流快,短时间内可能出现洪水陡涨局面,对黄河防汛安全威胁较大。区间内有伊洛河和沁河两条国家一级支流,是暴雨洪水多发地区。降水量年内分布不均匀,集中在6—9月。研究区有16个雨量站(图3),选取2009—2012年不同气象条件下8次降水事件的日降水数据来验证本文提出的基于Funk-SVD模型的降水时空插值方法(以下简称本文方法)。表 1为8个降水事件的详细信息,每场降水的空间分布如图4所示。这些降水事件持续时间为6~10 d,分布在6—9月,面降水量跨度很大,从17~67 mm,具有较好的代表性。

图3 黄河流域小浪底到花园口区间测站分布Fig.3 Distribution of gauge stations between Xiaolangdi and Huayuankou

图4 8场降水事件的降水量空间分布(单位:mm)Fig.4 Spatial distribution of rainfall in eight selected events
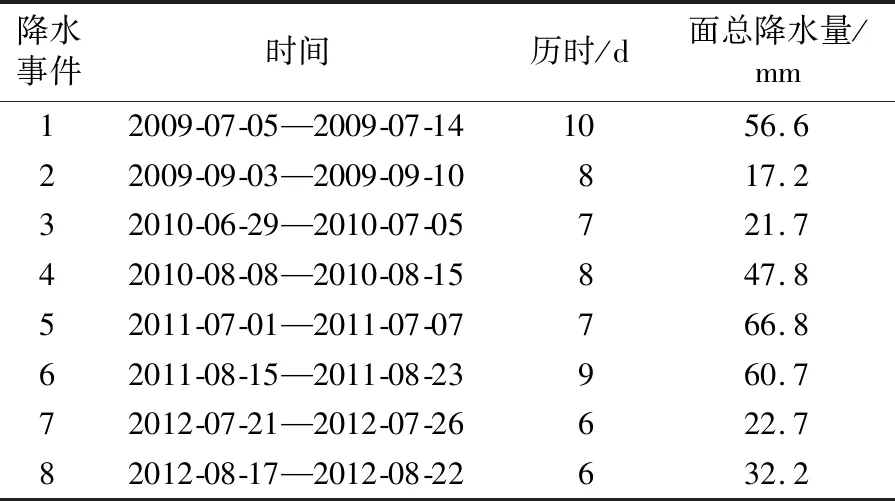
表1 降水事件信息Table1 Information of selected rain events
2.2 分解矩阵参数的影响
采用Funk-SVD模型利用矩阵进行插值时,需要m和N两个参数来确定矩阵的规模,其中m是插值所需的站点数,和矩阵的行数有关;结合N和插值时刻可以确定矩阵的列数。为了得到最佳的插值效果,对这两个参数选取了多种值进行演算和比较,结果见表2。可以看出,当m=7时,L达到最大值;当N=6时,RSME达到最小值,所以本研究中m取值为7,N取值为6。
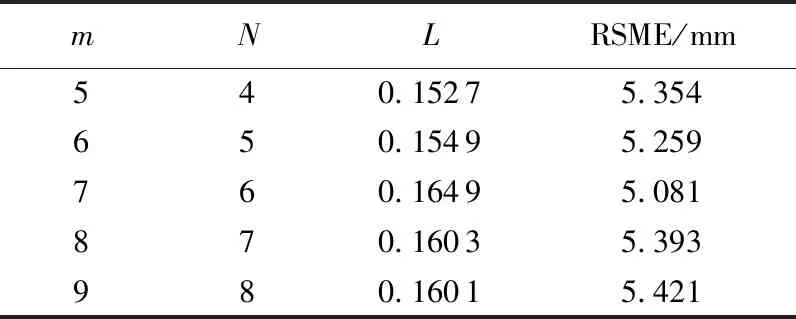
表2 不同m、N值的计算结果Table 2 Calculation results of different m and N
2.3 整体精度评价
使用4个不同的评价指标对各插值方法的计算结果进行了总体评价,结果如表3所示。从表3可以看出,4种插值方法的精度均在合理范围内,表明它们可以很好地应用于研究区域的降水插值计算。使用不同评价指标的评价结果是一致的,即通过与Funk-SVD结合,IDW和OK精度均得到了明显的提升。在RSME上精度提升了9%左右,在其余3个指标上的精度提升均在15%以上。除去KS,其他评价指标对IDW和OK的精度评价结果的差异很小,几乎可以忽略。
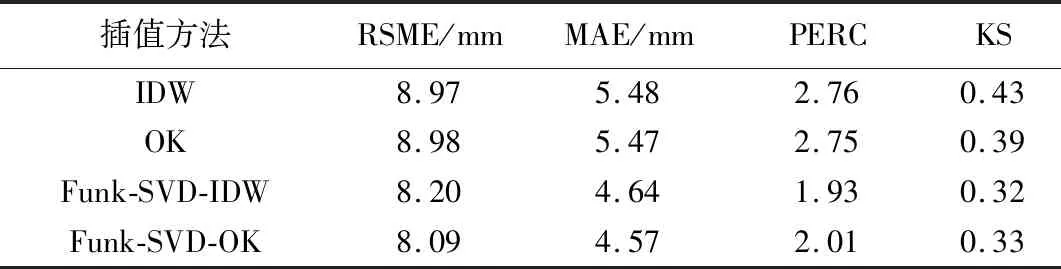
表3 8场降水事件的综合评价结果Table 3 Comprehensive evaluation results of 8 rainfall events
图5为4种插值方法在每场降水事件交叉验证中的所有站点的误差均值,可以看出,对于每一场降水事件,通过与本文方法结合,IDW和OK的精度在各项指标上均有所改善,这种改善在PERC和KS上更加明显。RSME和MAE对不同事件的评价结果是类似的,这是因为它们的数值与降水量大小有非常大的关联,所以降水量越大,计算得到的误差就越大。而对个别事件,使用PERC和KS会给出不一样的评价结果。比如5号降水事件,它的面总降水量是所有事件中最大的,所以绝对误差也大,相应RSME和MAE也最大;而PERC的数值大小与相对误差的关系更大,受绝对误差影响较小,因此PERC反而小。
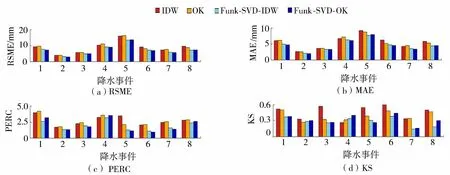
图5 降水事件插值精度评价结果Fig.5 Interpolation accuracy evaluation results of each rainfall event
2.4 代表性事件的站点误差比较
为了更好地评价本文方法的精度,选择5号大雨事件和7号小雨事件这两场典型的降水事件进行比较分析。图6和图7为使用不同插值方法得到的插值与误差结果。从图6和图7的(b)(c)和(e)(f)可以发现,无论是大雨还是小雨,降水量越大的点,往往插值产生的误差越大,并且大雨事件的插值误差会比小雨事件的大;同时,周围站点分布不均的点也会产生相对大的误差。图6和图7的(d)(g)中红色(改善)的点比蓝色(未改善)的点多,说明无论大雨还是小雨,通过与Funk-SVD结合,可以明显提升传统方法插值的精度。

图6 5号降水事件插值结果Fig.6 Interpolation results of No.5 rainfall event
3 结 语
本文基于站点的空间分布关系,利用当前时刻降水信息和历史降水信息,结合传统插值方法,提出了一种基于Funk-SVD模型的降水插值方法。采用黄河流域小浪底到花园口区间的8场降水事件中16个雨量站的日降水数据,通过交叉验证的方式对提出的方法进行精度检验,发现与Funk-SVD模型结合可以提升IDW和OK插值的精度,证实了本文方法的可行性。本文方法提高了降水空间估算的精度,为降水时空插值的相关研究提供了新的思路。

