基于时空特征挖掘的流量过程智能模拟方法
朱跃龙,赵 群,余宇峰,万定生
(河海大学计算机与信息学院,江苏 南京 211100)
近年来,全球气候变暖,极端降水事件频发导致了各种洪涝灾害,给人类带来巨大的经济社会损失。仅2020年全国共出现45次强降水过程,面降水量622 mm,较常年同期偏多13%,引发珠江、长江、黑龙江3个流域极端严重的流域性洪涝灾害[1]。为了减轻洪水灾害带来的不利影响,及时准确的水文预报显得尤为重要。水文预报是根据前期的水文气象资料,对未来一定时期的水文资料进行预报,对防洪救灾的决策、水资源的合理利用等具有重要意义[2]。
随着大数据时代的到来,基于数据驱动的水文预报模型在水文事件预报中越来越受到重视[3-4]。数据驱动的水文预报模型从历史水文资料出发,挖掘规律进行预测,为相关水利人员提供了一个新的预测方案。但现有基于数据驱动的水文模型大多侧重于从历史数据中学习时间特征,很少兼顾到数据的空间特征[5]。水文数据往往包含丰富的时空特征信息,而该特征信息可以为水文时空序列相似性,水文时空数据建模分析等作出贡献[6],本文提出一种基于时空特征挖掘的流量过程智能模拟方法GS-Hydro,构建水文结构关系图,利用图卷积网络挖掘空间特征的同时利用门控循环单元捕捉时间特征,以此提高预测精度。
1 水文预报模型相关研究
1.1 基于数据驱动的洪水预报模型
数据驱动模型是从数据着手,通过对时间序列数据的分析,从大量的数据中发现和揭示数据的发展变化规律,以此估测和控制未来可能出现的状况。基于数据驱动的洪水预报模型从历史水文资料出发,挖掘规律进行预测,相较于其他水文模型具有普适性。
Hwang等[7]提出一种基于最小二乘支持向量机(LS-SVM)的非线性水文时间序列预测方法,具有较好的预测精度和预测性能。Xing等[8]提出一种新的启发式优化算法BA算法,用于优化SVM参数和预测2015年月平均流量,其预测精度比交叉验证的支持向量机更高。Atiquzzaman等[9-10]针对传统基于梯度的慢学习算法在训练和迭代确定网络参数时的不确定性问题,提出一种基于极限学习机(ELM)的水文时间序列快速预测方法。根据洪水形成的基本原理,Chen等[11]提出一种基于数据驱动和机器学习的卷积回归水文预报模型,该模型能够反映小时降雨量对未来流量变化的影响,并通过叠加这些影响预测流量变化。
1.2 基于时空特征的预报模型
除了时序特征,自然界大部分的数据还具有空间结构联系。相比于单一的时序预测,基于时空特征结合的预测考虑了数据之间的空间特性,能够挖掘出更多的信息规律,提高预测精度,而空间特征与时间特征的结合预报也被广泛地运用到了各大领域[12-13]。
Ding等[14]利用长短期记忆模型,提出洪水预报模型(STA-LSTM模型),动态提取关键特征向量,实现中小河流洪水预报。除此之外,空间特征也可用于水文学的许多方面,如水文相似性分析[15]、流域场景模式库构建[16]、用水效率分析[17]等。
目前基于数据驱动的水文预报模型大多考虑时序特征,很少考虑河流之间的地理联系和空间特征。单一测站的水文数据具有时间连续性、周期性,而将多测站的水文数据放在一起,不难看出它们之间的空间联系。本文提出一种基于地理关系的时空智能流量过程模拟模型,通过地理关系建立测站之间的结构联系,辅助预测目标测站的流量值。
2 基于时空挖掘的智能流量过程模拟模型
现实世界中存在大量的图结构或网络结构数据,传统的卷积神经网络(convolutional neural networks,CNN)难以处理。为了解决这一问题,一种处理图结构网络的半监督分类方法——图卷积神经网络(graph convolutional networks,GCN)[18]被提出,并被广泛应用于社会网络、信息网络等领域的特征学习。与CNN不同,GCN对图像进行像素卷积,并可以挖掘网络结构。目前,GCN主要对社会网络、信息网络等非结构化数据提取特征进行学习,然而很少有人在水文时间序列数据中使用。
本文构造了一种新的水文站点地理位置关系图,利用GCN挖掘空间特征,再利用门控循环单元(GRU)[19]挖掘时间特征,进一步进行水文预报,方法结构如图1所示,图中Xt为t时刻的输入样本,Ht为模型输出。
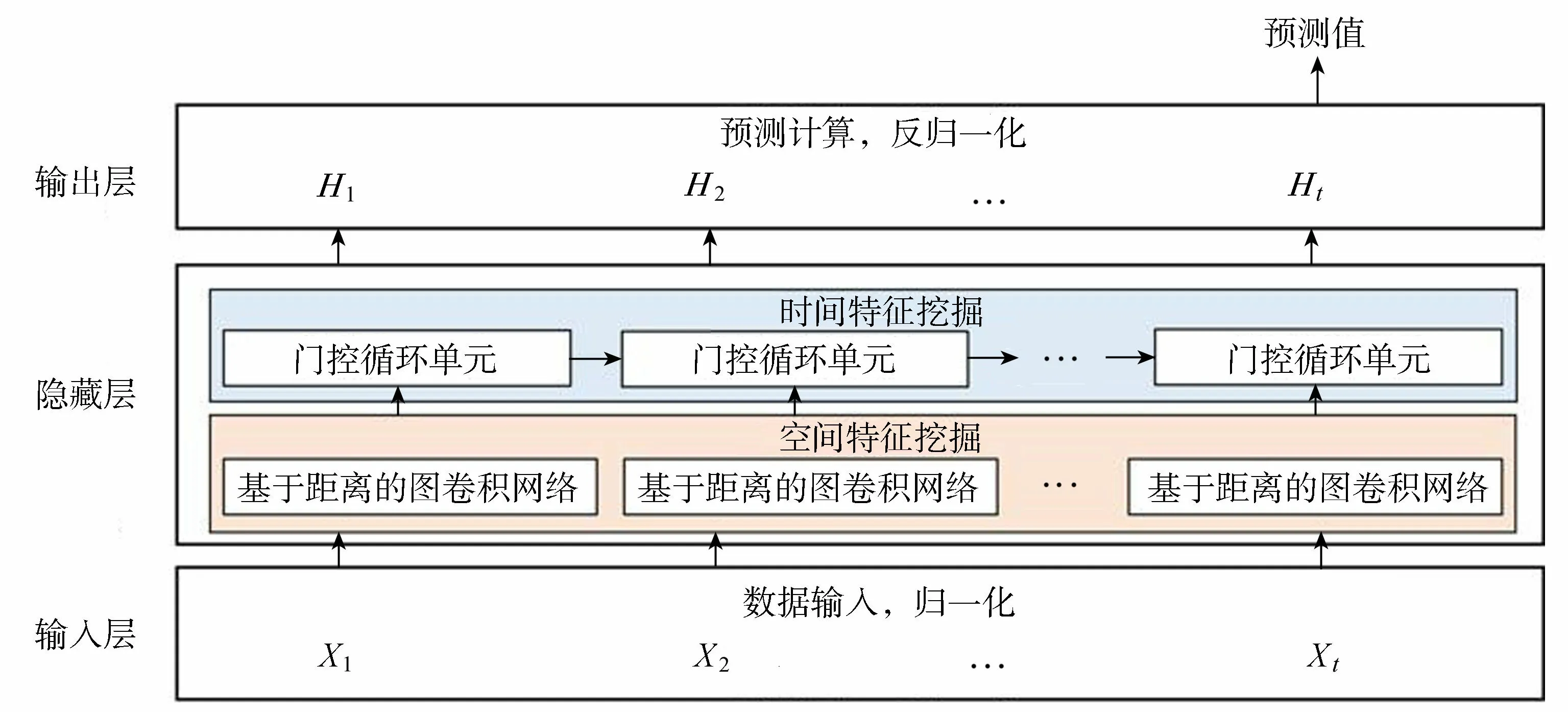
图1 GS-Hydro模型结构Fig.1 Structure of GS-Hydro model
输入层,以河流流量信息和当前时段面平均雨量信息为自变量,实现数据规范化、训练集划分、验证集划分、测试集划分等。隐藏层,在空间方面利用图卷积神经网络捕捉河流复杂的网络特征;在时间方面利用门控循环单元将前一时刻的信息传递到下一时刻,其中的更新门和复位门可以更好、更快地确定信息,为模型留下更多有价值的信息。输出层,对数据进行反规范化处理,并对输出结果进行预测。
2.1 基于距离的水文测站关系结构图
2.1.1 水文测站关系结构图的建立
结构图的生成是训练图卷积网络模型的第一步,也是重要的一步。如果结构图不能很好地反映节点之间的关系,模型可能无法有效地挖掘信息。定义水文测站关系结构图如下:
G=(V,E)
(1)
式中:G——水文测站地理位置关系图;V——节点,指各个水文测站;E——连接点边的集合,指各个水文测站间的地理关系。
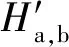
河道距离是目标流域到它的上游流域之间的河流长度,根据DEM估算。当每个网格中的水以最陡的坡度流向其相邻网格时,可以找到水从任何点到海洋或者从研究区域流出的流动路径。如果上游的水流经过下游的水流,则河道距离是它们之间的流路长度。如果它们没有河道联系,则河道距离为零。
邻接矩阵是存放节点间关系(边或弧)数据的数组,定义如下:
(2)
式中:ai,j——邻接矩阵中第i行、第j列的元素;α、β、δ——矩阵中元素的系数。
对模型进行训练拟合出适合的α、β和δ,然后求出水文测站地理位置关系图的边,以此构造水文测站地理位置关系结构图。值得注意的是,当地理距离较大且没有河道距离时,2个水文测站的流量变化几乎没有关联,本文对水平距离100 km以内的站点计算节点间的关系。
2.1.2 图卷积操作
本文使用图卷积网络对各测站进行空间特征挖掘,如图2所示。

图2 空间特征提取Fig.2 Spatial feature extraction
图卷积网络定义如下:
X(l+1)=f(X(l),A)
(3)
式中:l——层数;X(l)——l层节点的特征;A——邻接矩阵。
首先输入特征矩阵和邻接矩阵,然后对节点进行特征变换,用度矩阵对邻接矩阵进行归一化。加入自循环后,考虑每个节点与相邻节点之间的关系,具体模型如下:
(4)
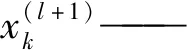
2.2 基于时空特征的智能流量过程模拟模型
进行空间特征提取后可以对时间特征进行处理,本文使用门控循环单元(GRU)进行时间特征的提取。GRU可以改进长短时记忆网络[21](LSTM)的门设计,克服梯度消失问题。同时,它具有更快的收敛速度,改善了LSTM训练耗时的问题。
设定模型损失函数为均方误差函数e,计算公式如下。
(5)
式中:yt——t时刻的预测值;Yt——t时刻的真实值;n——模型输入的样本数目。
模型具体计算过程如下。
a.空间特征提取(以两层卷积为例):
(6)
b.更新门构建:zt=σz(Wz[ht-1,f(Xt,A)])
(7)
c.重置门构建:rt=σr(Wr[ht-1,f(Xt,A)])
(8)
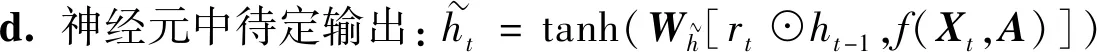
(9)
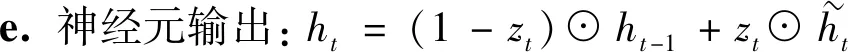
(10)

通过全连接层得到最终输出:yt=O(Wcht+b),其中O(·)为线性函数;Wc为权重;b为偏置。
3 试 验 分 析
3.1 数据集
试验选取江西省鄱阳湖流域外洲站作为模型流量过程测试站点,如图3所示。试验选取外洲站1998—2010年夏季小时时段洪水流量21 060条数据以及降雨资料作为数据,对区域内雨量站的降雨量进行算术平均从而获得面降雨量,选取前6 h内的小时时段降雨作为降雨信息对流量预测提供辅助,区域内选取的雨量站如图4所示。由于部分降雨不完全,采用水文中常用的线性插值方法对缺失的雨量进行补充。试验以各个水文站为节点,站点之间的地理关系为邻接矩阵,各站点的历史小时流量数据和小时降雨数据为特征矩阵。试验使用60%的数据集作为训练数据集,20%作为验证数据集,20%作为测试数据集。
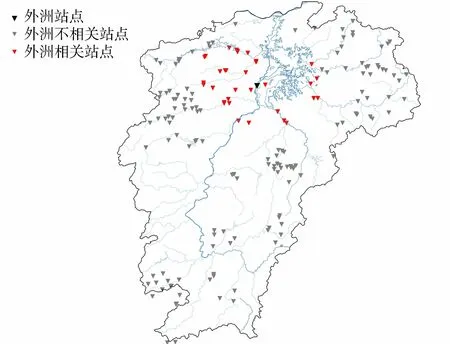
图3 江西省试验模拟测试站点Fig.3 Experimental simulation test stations in Jiangxi Province

图4 外洲站周围雨量站示意图Fig.4 Schematic diagram of rainfall stations around Waizhou Station
3.2 评价指标及参数选取
评价指标采用均方根误差和确定性系数。采用支持向量机模型(SVM)[22]、长短时记忆网络(LSTM)、门控循环单元(GRU)和提出的GS-Hydro模型进行训练。训练参数根据试验调试,最优超参配置如下:SVM的惩罚系数为0.3,核函数为径向基核函数,区间为0.05。LSTM的隐节点数为100,学习因子的区间为0.005,批处理大小为128,迭代次数为40。GUR中隐藏节点数为50,学习速率为0.005,批处理大小为32,迭代次数为50。GS-Hydro模型中的隐藏节点数为32,学习速率为0.005,批处理大小为64,迭代次数为100。
3.3 试验结果分析
外洲站SVM、LSTM、GRU和GS-Hydro的模型流量3 h预见期预测模拟计算结果如图5所示,不同模型在模拟预测中的评价指标见表1。
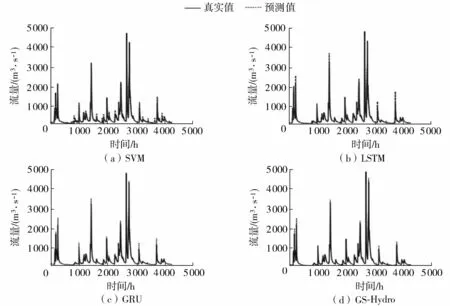
图5 江西省外洲站3 h预见期下各模型流量预测结果Fig.5 Runoff prediction results of Waizhou Station in 3-hour forecast period with different models

表1 各模型预测结果评价指标对比Table 1 Comparison of prediction results of different models
从图5中可以看出,SVM的预测结果比较抖动,得到的预测曲线不如LSTM、GRU和GS-Hydro稳定。LSTM和GRU的预测结果相似,GS-Hydro比GRU好,比LSTM更稳定。
从表1可以看出,1h流量预测相对最准确,预见期越长,精度越低。GS-Hydro是所有不同预测期的最佳模型,LSTM和GRU的性能略好于GRU,支持向量机表现最差。GS-Hydro的确定性系数最高,LSTM与GRU的差异不显著,SVM稍差。因此,GS-Hydro模型在整体预测结果中是最好的,是因为GCN捕捉了流量的空间特征,在预测过程中加入了空间内多个相关站的雨量,避免了梯度消失和均值漂移的问题。
4 结 语
本文提出了一种新的流量过程智能模拟方法GS-Hydro,该方法将图卷积网络(GCN)与门控循环单元(GRU)相结合,先建立基于河道关系的水文站点地理位置关系图用以进行特征挖掘,再将GCN用于获取样本的空间特征,GRU用于捕捉样本的时间特征。试验表明GS-Hydro模型的性能优于其他神经网络模型。

