Alpha稳定噪声中频移键控信号的联合同步估计
孙明杰,周 林,刘永进,顾金玲,石 磊
(1.空军工程大学防空反导学院,陕西 西安 710051;2.中国人民解放军93861部队,陕西 咸阳 713800;3.中国人民解放军32272部队,甘肃 兰州 730060)
0 引言
传统的通信方案中通常都假设噪声符合高斯分布;然而,在很多方案中,噪声通常不符合高斯分布并且具有明显的脉冲特性。例如,在甚低频和低频(VLF/LF)通信和水下通信中,脉冲噪声广泛存在,这意味着采样信号将会被严重破坏。在这种情况下,采用高斯噪声的方法在信号处理过程中通常会得到较差的结果。根据文献[1—3],噪声采用α均匀稳定(SαS)分布建模而不是高斯分布将更有吸引力,这是因为α均匀稳定(SαS)分布的概率密度函数能够更好地描述脉冲噪声中的脉冲。
SαS分布噪声的通信和信号处理已成为研究热点[2-9]。由于SαS分布噪声广泛存在于VLF/LF通信中,本文主要对频移键控(MSK)的联合时间相位同步问题进行研究[1,10]。显然,在评估脉冲噪声同步算法时,给出同步算法的性能界限是很有必要的[11],然而,目前关于性能界限的分析并不多。有关高斯噪声中的频移键控同步已有研究[12]。在SαS噪声中,同步算法的基本原则如下:接收到的信号首先经过非线性抑制噪声预处理,然后再利用高斯噪声的同步算法[2,13]。
本文推导了关于频移键控信号联合时间相位偏移的克拉美罗下限,设计了一种最小化克拉美罗下限的最优训练序列,提出一种估计两个同步参数的实用算法,并进行了相关仿真。
1 信号模型
在VLF/LF通信中,MSK信号被广泛采用,噪声服从α均匀稳定(SαS)分布[1,10]。同时,VLF/LF通信信道是频率衰落信道。基于已知训练序列的数据辅助同步算法估计参数[12],令d{l},l=0,…,L-1,T与Ts分别代表MSK传输信号的训练序列,采样间隔和符号周期。接收到的训练序列基带采样信号为[8]:
(1)
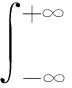
式(1)中,q(nT)为MSK信号的相位响应,当0≤nT SαS分布有两个参数,特征参数0<α≤2和数值参数γ>0[2],α越小,存在的脉冲越多。除特殊个例,SαS分布没有显式概率密度函数表达式。但存在显式性能函数[2]φ(ω)=e-γα|ω|α。令υ0,R(n)和υ0,I(n)分别为α和γ。接收信号的SNR为: (2) 为了方便表示,采用功率标准化接收器模型如下: (3) 式(3)中,p=[p1,p2]T=[τ,θ]T为同步参数矩阵,υ(n)=υ0(n)/γ归一化复基带SαS噪声信号。 本节将主要讨论p估计的CRLB。令向量r=[rn]T=[r(n)]T,s=[sn]T=[s(n,p)]T,e=r-s=[en]T,其中n=0,…N-1,N为接收信号的采样数目。则用来估计p的最大似然函数可以表示为: (4) 根据噪声模型,en,R和en,I服从特征参数α数值参数为1 的SαS独立同分布,f(·)为en,R和en,I的概率密度函数。 另外,p估计的费舍尔信息矩阵(FIM)I(p)∈2×2为[11]: (5) 式(5)中,i,j=1,2;g(x)为SαS分布的评分函数,表达式为: g(x)=-f′(x)/f(x) (6) 当x趋近于无穷时,概率密度函数f(x)服从f(x)~(αCα/2)x-α-1,其中,Cα是由α决定的常数。期望E[g′(en,R)]为: (7) 同样的,可以得到E[g(en,I)]=0,则: (8) 费舍尔信息矩阵可表达为: (9) 将式(1)中的MSK信号表达式代入式(3),[τ,θ]T估计的CRLB为: CRLB{τ}=[I-1(p)]1,1= (10) CRLB{τ}=[I-1(p)]2,2= (11) 式(10)、式(11)中,κ(α)揭示了参数α对CRLB的影响。根据κ(α)的性质,当α≥1时,随着α的减小,CRLB基本不变;当α<1时,CRLB随着α的减小迅速减小。同时,大的采样数目N,例如,大的过采样频率,导致更小的CRLB。进一步,由于CRLB是TS{dl}的函数,可以设计最优的TS最小化CRLB。显然,最优TS应该满足: (12) 本节提出一种同步参数向量p=[τ,θ]T的估计算法。p的估计值是下面优化问题的解: (13) 式(13)中,J(r,p)为成本函数。最优成本函数可以根据LLF设计,然后可以得到MLE。但是由于LLF没有闭式形式,因此很难在SαS中得到MLE。为了设计一种实用算法,本文提出一种闭式极大成本函数。与基于成本函数的最优LLF相比, 极大成本函数性能近似最优,并且已经用来设计SαS噪声中的自适应滤波器和信号检测[4-5]。极大成本函数可以表示为如下形式: (14) 根据文献[5],极大成本函数为非凸的,因此可以采用全局搜索方法对优化问题式(13)进行求解。本文选用一种典型的全局搜索方法—分支定界法[15],向量p的搜索空间首先被分为多个子空间,对每一个子空间,如果包含全局最优解,则将该子空间继续分割,否则,直接删掉该子空间。分支定界法的关键在于在子空间中找到成本函数J(r,p)的边界。 已知向量p的搜索空间为矩形区域,因此,将搜索空间分为小的矩形区域,小矩形的每个顶点对应一个向量p。下面介绍在子矩形区域中推导基于下边界的Lipschitz常数的定理。 令p1和p2代表一组子矩形区域的对角,则基于J(r,p)下边界的Lipschitz常数满足 (15) 其中Lipschitz常数C为: (16) 证明:令 (17) 在p1和p2为对角的子矩形区域中,基于Jn,R(r,p)下边界的Lipschitz常数满足[15]: (18) 式(18)中,Cn,R为对应的Lipschitz常数,等于‖∂Jn,R(r,p)/∂p‖的上确界[15]。 (19) 其中, (20) 在VLF/LF通信方案中,脉冲噪声的幅度通常要比传输信号的幅度大[9-10]。由此,可得: (21) 最后,可得Cn,R为: (22) 同样,可得基于J(r,p)下界的Lipschitz常数 (23) 综上所述,可得基于J(r,p)下边界的Lipschitz常数如式(18)所示。 通过上述分支定界法,提出的同步算法图1所示。 图1 同步算法流程图Fig.1 The flow chart of synchronization algorithm 1) 复杂度。对于本文提出的算法,算法复杂度主要由算法流程和迭代次数决定。在算法流程图中,复杂度主要来自于极大成本函数J(r,p)的计算。J(r,p)在步骤21中需要计算8次。根据式(6),J(r,p)的计算需要4N次加法,2N次乘法和2N次对数运算。同时,仿真表明算法流程的多次迭代能够保证所提算法收敛。 在仿真中采用了点对点的VLF/LF通信系统,该系统包含了MSK信号和SαS噪声。设置TS中的符号数为L=20,时偏τTs和载波相位偏移θ分别落在区间[0,Ts)和[0,2π)。给出在信噪比η下的同步性能。另外,根据式(12)设计了最小化CRLB的最优TS。算法1中的结束点设置为ε=0.001。 在SαS噪声中,已有的同步算法包括基于高斯的非线性预处理同步方法[2,9]。由于剪切的使用,可以较好处理非线性问题[2,13],被称为基于剪切的同步算法。根据文献[12],当存在高斯噪声时,基于高斯的同步算法能够得到: (24) 图2对基于剪切的算法和本文算法的CRLB估计点进行了比较。其中参数α和过采样率Ts/T分别设置为1.5和10。从图2可以看出,与基于剪切的算法相比,本文所提算法具有更好的性能,接近CRLB。主要原因是极大成本函数在SαS噪声中具有近似最优的性能。 图2 基于CRLB算法和基于剪切算法的θ(左)和τ(右)的估计性能比较Fig.2 Comparison of estimated performance (left) and (right) based on CRLB algorithm and shearing algorithm 图3展示了在不同估计误差Δη和Δα下θ和τ的估计点。能够看出,根据前面ECF方法估计得到的η和α设置的估计误差Δη和Δα对所提方法基本没影响。 图3 不同估计误差Δη和Δα下θ和τ的θ(左)和τ(右)的估计Fig.3 Estimates (left) and (right) of the lower sums of different estimation errors 本文提出显式极大代价函数和全局最优的实际同步参数估计算法。该算法得到了时间和载波相位偏移联合估计的CRLB,并设计了最优TS使得CRLB最小。仿真结果表明,所提方法性能基本接近CRLB,仿真结果也证明该方法对由信噪比和噪声参数引起的估计误差鲁棒。2 同步算法设计
2.1 克拉美罗下限分析


2.2 同步算法流程
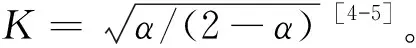

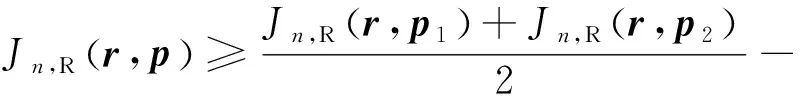

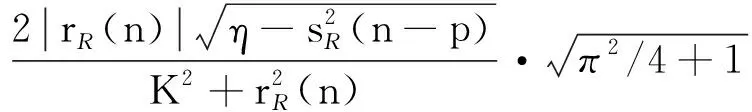
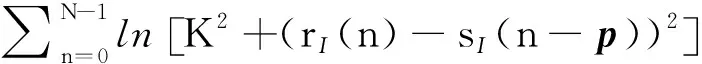

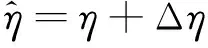
3 仿真验证


4 结论

