基于最大累计度量的低复杂度多指数CPM信号解调
郑志东,肖庆正,吴高洁
(1.北方电子设备研究所,北京 100191;2.国防大学联合作战学院,北京 100091)
0 引言
连续相位调制(CPM, continuous phase modulation)信号[1]有着许多优良的特性,因此一直以来都是人们研究的热点。首先,CPM信号是一个恒包络信号,因此其可以使用高效率低成本的非线性放大器进行放大;其次,CPM信号有高带宽效率以及快旁瓣衰落的特性[2];最后,CPM信号有灵活的调制指数,不同的调制指数可以得到不同的CPM信号波形,从而适应不同的应用场景。多指数CPM信号(Multi-h CPM)相比于单指数CPM信号(Single-h CPM),具有更高的频谱利用率,另外,Multi-h CPM信号引入了调制指数集的概念,这使得信号之间的最小欧式距离更大,因此Multi-h CPM信号相比单调制指数CPM信号有着更好的解调性能[3]。
然而,Multi-h CPM信号具有更高的解调复杂度,以往研究主要通过以下两种方式来降低解调复杂度[4-11]:第一种是减少接收端匹配滤波器数量,常见方法有Laurent分解[4-5]、脉冲截断(FPT, frequency pulse truncation)[5]等;第二种是减少网格状态数量,常见方法有倾斜相位[6]、减少状态序列检测(RSSD, reduced state sequence detection)算法[7-8]、逐幸存(PSP, per-survivor processing)算法等[9-11]。减少网格状态数量的算法在单调制指数CPM信号中有着较好的效果,但是在Multi-h CPM信号中性能不佳,文献[12]将PSP用在Multi-h CPM信号检测中,提出了一种基于虚拟调制指数集(VhD, virtual indexes(h) detection)的降复杂度方案。该方案对某些特定调制指数集有着较好的性能,但是对于其他的调制指数集性能较差;另外,当改变调制参数时,该方案需要重新确定调制指数集来获取较好的检测性能,因此不具有良好的普适性。本文针对多指数连续相位调制(Multi-h CPM)信号解调的高复杂度问题,提出基于最大累计度量的低复杂度多指数CPM信号解调方法。
1 Multi-h CPM信号模型
1.1 Multi-h CPM信号及其倾斜相位表示
CPM信号的等效复基带表达式可以表示为[1]:
(1)
式(1)中,E表示每个符号的能量,T表示符号周期,αi∈{±1,±3,…,±(M-1)}表示符号序列,M表示调制阶数,ψ(·)表示信号的相位。CPM信号的相位又可以进一步表示为:

(2)

g(t)为频率响应函数,持续时间为LT,q(t)满足当t>LT时,q(t)=1/2;当t<0时,q(t)=0。L为记忆长度。当L=1时,信号被称为全响应CPM信号;当L>1时,信号被称为部分响应CPM信号。
CPM信号在t=nT时刻的状态可以表示为:
σn={θn-L,αn-L+1,αn-L+2,…,αn-1}
(3)
式(3)中,θn-L表示相位状态,σn′={αn-L+1,αn-L+2,…,αn-1}表示相关状态。因此可以发现,CPM信号在t=nT时刻的总状态数为mML-1,m表示相位状态的总个数。如果令h=k/p,其中k,p为互质数,则有m=p,p为奇数;m=2p,p为偶数。使用倾斜相位的思想后[6],相位表达式可以写为:

(4)
式(4)中,
1.2 Multi-h CPM信号的PAM分解
Laurent-Mengali最早指出,单调制指数CPM信号可以由一组有限数量的脉冲幅度调制(PAM, pulse amplitude modulation)波形信号精确表达[4],这种方法也被称为PAM分解。2005年,Perrins又将上述分解方案推广到Multi-h CPM信号[5]。Multi-h CPM信号的PAM分解表达式可以表示为:
(5)
通过PAM分解,可以减少接收端匹配滤波器的数量。以MIL-STD-188-181C标准中的Multi-h CPM信号的参数为例,M=4,h=[4/16,5/16],1REC信号一共有3个PAM波形,奇数时刻的PAM波形如图1所示。
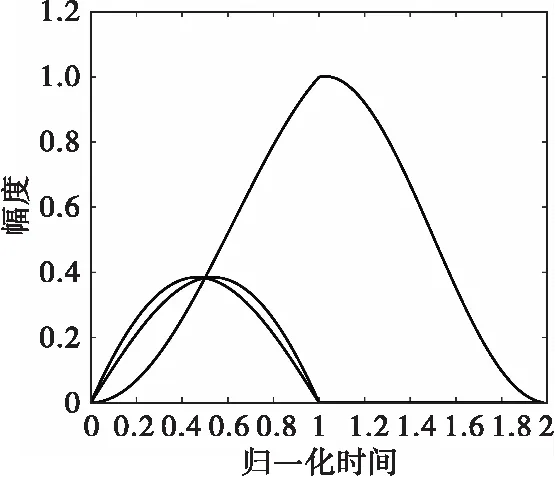
图1 奇数时刻MIL-STD-188-181C标准中的Multi-h CPM分解脉冲波形图Fig.1 The decomposed Multi-h CPM pulse waveforms of MIL-STD-188-181C standard signal at odd time
2 Multi-h CPM接收机
假设发送信号经过高斯白噪声信道,接收端表达式为:
r(t)=s(t;α)+n(t)
(6)
式(6)中,n(t)表示零均值加性高斯白噪声。接收信号通过匹配滤波器得到信号的分支度量值,然后送入状态网格中进行Viterbi译码,最后经判决可得到检测的发送信息。
2.1 极大似然序列检测(MLSD)接收机
在MLSD解调算法中,因为CPM信号是一个恒包络信号,所以极大似然等价于最大相关[13]。

(7)
将式(6)带入式(7)可得递归路径度量表达式为:

(8)
式(8)中,λi(n-1)表示第i条幸存路径累积到t=(n-1)T时刻的度量值,式(8)右边第二部分表示当前符号周期产生的分支度量值,该项可以进一步改写为:
(9)

图2 MLSD解调接收机原理框图Fig.2 The diagram of the MLSD-based receiver
2.2 基于PAM分解的接收机
与MSLD相比,基于PAM分解的接收机只在计算分支度量时有所不同。具体计算过程为:
(10)
(11)
式(11)中,Dk表示第k个PAM脉冲波形持续的时间。对于PAM次最优分解,只需要将上式中的N替换为M-1。因此PAM最优分解情况下需要的匹配滤波器数量为N,次最优分解情况下需要的匹配滤波器数量为M-1。图3为基于PAM最优分解接收机原理框图。
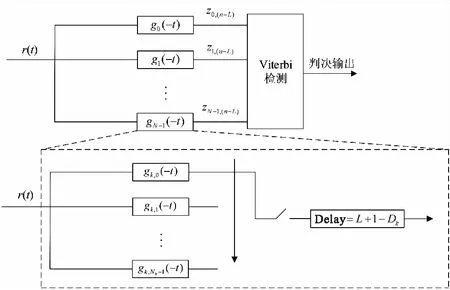
图3 基于PAM分解的解调接收机原理图Fig.3 The diagram of the receiver based on PAM decomposition
3 基于最大累计度量的降复杂度方法
Viterbi译码[14]的过程是一个“加、比、选”的过程。假设网格一共有I个状态,每个状态分别可以延伸出M条路径,则第(n+1)T时刻的路径更新可以写为:
(12)

如图4所示,我们假设一个四状态网格转移图,实心圆表示真实路径,实箭头表示现阶段的幸存路径,虚线箭头表示在Viterbi算法中舍弃的路径。在t=3T时刻,保留下来的幸存路径有四条,此时它们的累积度量值是不同的,累积度量值越大则代表和真实路径的差距越小,我们不妨假设:

图4 网格状态转移示意图Fig.4 The diagram of grid states transition
(13)

在Viterbi算法中,这些路径对应的累积度量值都会保留,在t=nT时刻,将各个状态对应的累计度量值排序如下:
(14)
式(14)中,bi∈{1,2,…,I},i为状态bi对应的次序。我们每次保留N′(0 (15) 通过删减每一时刻累计度量值较小的幸存路径,进而降低后续时刻的计算复杂度。 另外,以上提出的改进算法是针对减少网格状态数量的方案,因此我们可以结合其他针对减少匹配滤波器数量的方案[4-5],从而进一步降低接收机复杂度。本文中,我们采用PAM分解方案来减少匹配滤波器的数量。 为了验证上述改进方案的有效性,我们首先比较本文提出的基于最大累计度量的MLSD(MLSD-CM)算法与传统MLSD算法的性能。仿真采用MIL-STD-188-181C标准中的Multi-h CPM(M=4,h=[4/16,5/16],1REC)信号,该信号共有32个网格状态。 从图5中可以看出,当N′=8时,MLSD-CM算法在性能上基本没有损失,当N′=4时,有约0.5 dB的性能损失。在MLSD算法中,我们需要计算32个网格状态的分支度量值,而使用了MLSD-CM算法,我们只需要计算6个网格状态的分支度量值即可,计算复杂度得到了极大的降低。 图5 基于最大累计度量算法在MLSD中的误码性能Fig.5 The BER performance of MLSD-CM alogrithm 本节结合PAM的分解方法,进一步降低接收端匹配滤波器的数量,仿真结果如图6所示。 图6 改进算法结合PAM分解的误码性能Fig.6 The BER performance of the PAM-CM method 如图6所示,当N′=8,6时,PAM-CM算法性能上都损失极小;当N′=4时,PAM-CM算法有约0.35 dB的性能损失。同时,表1给出了图5和图6中方案复杂度分析。 表1 不同方法的复杂度对比Tab.1 The complexity comparison of different methods 从表中可以看出,结合了PAM分解的改进方案可以同时降低接收机匹配滤波器的数量和网格状态数量,并且当合理的选择N′时性能损失极小。另外,在我们提出的算法中需要对每符号周期的累计度量值排序,每周期排序长度最多为MN′。 以另一组参数进行仿真,同样采用MIL-STD-188-181C标准中的Multi-h CPM(M=4,h=[5/16,6/16],1REC)信号,该信号共有32个网格状态。仿真结果如图7所示,结果表明,更改了仿真参数后,所提算法依然有着很好的解调性能,因此只要选择的N′合适,该算法就可以极大地降低接收机的复杂度。 图7 改进算法结合PAM分解的误码性能Fig.7 The BER performance of PAM-CM decomposition method 本文提出一种基于最大累计度量的低复杂度解调方法,该方法通过引入最大累计度量值,比较网格状态中的大小进行网格状态删减,进而达到降低网格状态数量,在此基础上,结合PAM分解,进一步减少了接收端匹配滤波器的数量,简化了接收机结构。为了验证所提方法的有效性,我们采用MIL-STD-188-181C标准中的信号进行仿真实验。仿真结果表明,与传统的极大似然序列检测(MLSD)相比,本文算法在基本不损失解调性能的基础上,可以极大地降低网格状态数量与匹配滤波器数量。
4 仿真性能分析
4.1 基于最大累计度量的MLSD算法误码性能

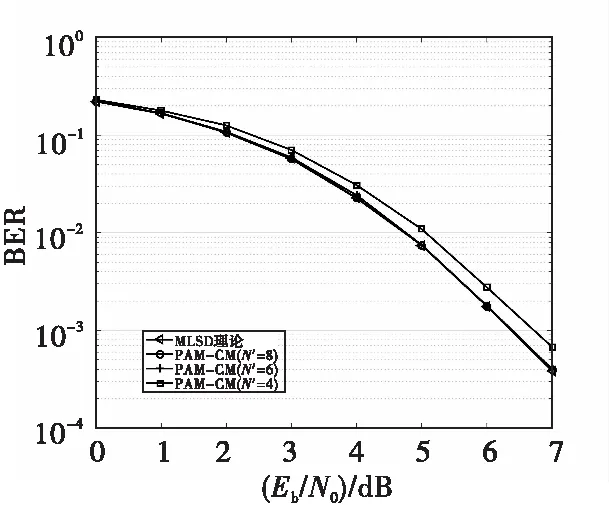
4.2 基于最大累计度量和PAM分解算法误码性能


5 结论

