《圆》教学实践及思考

沙欣

【摘要】本文以《圆》教学为例，引导学生把握《圆》的教学核心，借助实例使学生进行过程性思考，促进学生对图形的认识，培养学生的空间思维能力。

【关键词】《圆》 图形本质 图形教学

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2021）41-0091-02

在小学图形与几何教学中，为了让学生在学习中深刻地认识图形，教师应紧扣图形的本质特征进行课堂设计，发展学生的空间观念。现以人教版数学六年级上册教材《圆》这个单元的教学为例，探讨通过把握图形的本质特征，引导学生展开过程性思考，从而有效提高学生的数学思维能力。

一、把握《圆》的教学核心

在小学阶段，学生认识的第一个曲边平面图形就是圆。为了研究圆这个图形，学术界主要运用了直线逼近曲线（用有限逼近无限、用有线线段逼近曲线）的思想方法，这种方法是一种切割术，以逼近极限的方法以直代曲（如图1）。而用这种方法进行课堂教学，并在此基础上向学生渗透极限思想（如图2），这对小学生而言过于抽象，也很难理解，这也成为了课堂教学的难点之一。

由此可知，圆的研究方法就是数学教学的核心之一。教师要引导学生把握圆的普遍性、对称性、均匀性这三个基本特性，更好地把握教学的核心，也就是以直带曲的研究方法。在教学实践中，教师要引导学生逐步积累认识圆这种曲边图形的研究方法。在后续的学习中，学生还将学习圆的周长、圆的面积等内容，只有把握圆的本质及其研究方法，才能够掌握圆的周长、面积的推导方法及推导过程，从而将这些方法顺利地应用于实际生活当中。

在《圆》这一单元的学习中，学生掌握了圆的学习方法之后，就能够自然进入圆的周长和圆的面积学习。教师要特别关注圆的周长与面积计算公式的推导过程，以及在这个过程中引导学生进行积极思考。比如，在圆的周长推导过程中，借助圆的滚动，以直代曲，讓学生关注图形的位置及对应关系。（如图3）

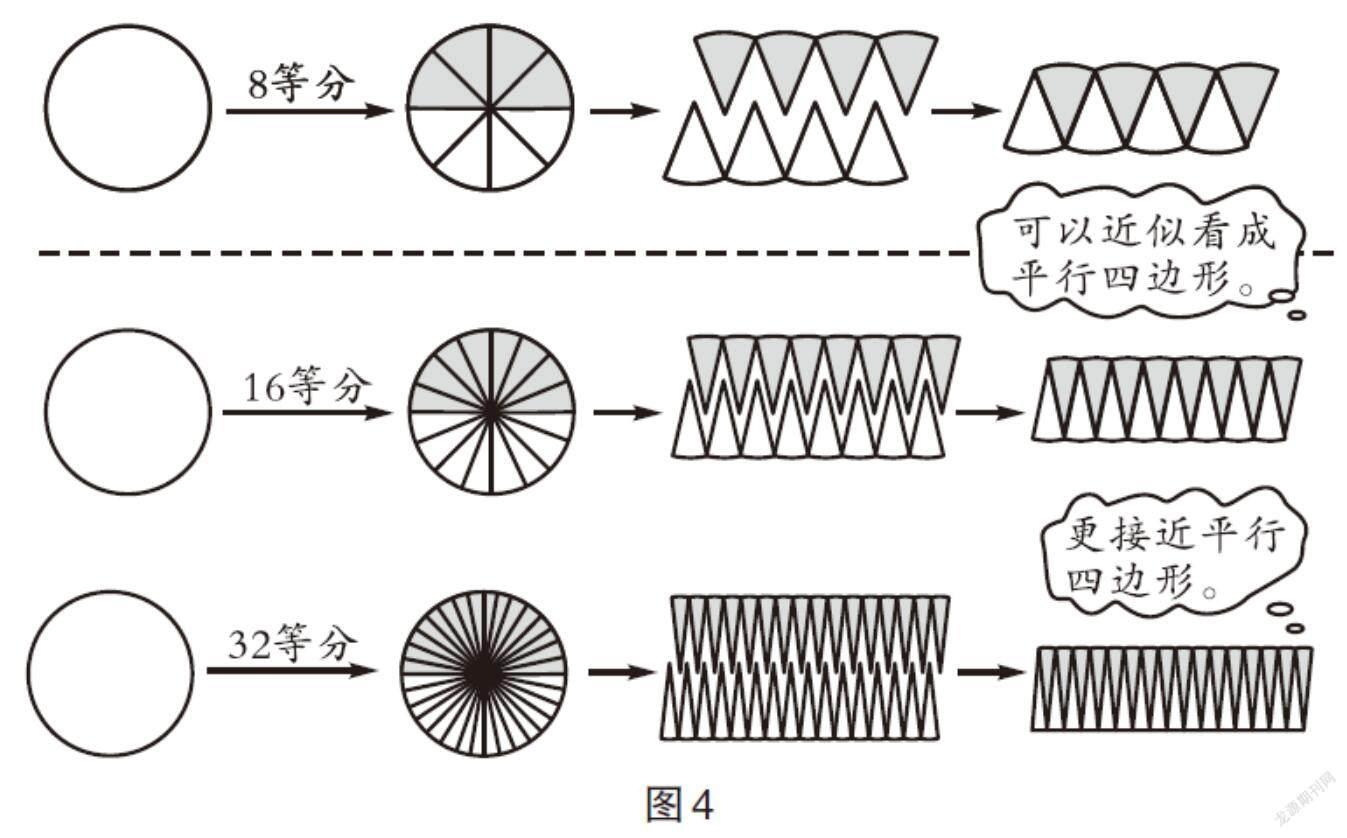
再如，在圆的面积推导过程中，借助以直代曲的方法进行推理（如图4），学生能够关注图形的变化，从而对圆的本质特征有了深刻的认识，发展了空间思维能力。

二、引导学生进行过程性思考

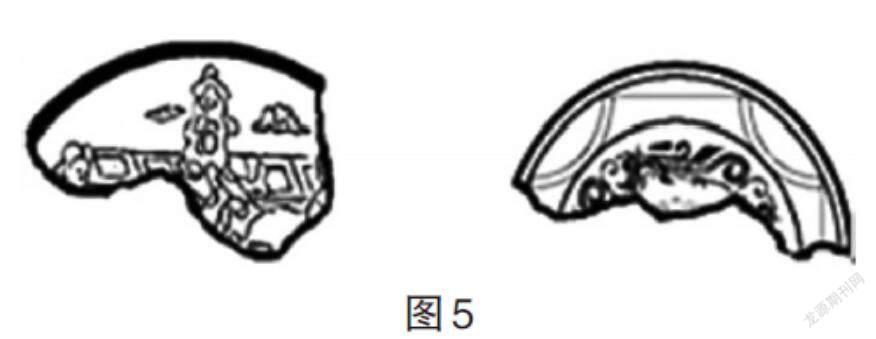
明确了课堂教学的核心，接下来需要推动学生进行过程性思考，让学生对圆这一图形形成本质的理解。为此，笔者设计了一些评价性的数学题目，一方面检测学生所学，另一方面能够倒逼学生进行自主思考，对圆的本质特征进行再认识和再理解。比如，为了让学生对圆的各点均匀性形成深刻的理解，笔者设计了这样的一道题目：对比两块圆形铜镜的边缘残片，看看哪一块铜镜的面积大（如图5）。学生依据圆的本质特征展开思考，找到两种方法：其一，想象还原圆的整体，从而认识到圆越大，弯曲的程度就越平缓;圆越小，弯曲的程度就越大，由此可以根据圆的弧度判断其大小;其二，延长外圆找到半径，根据半径的长短进行判断。

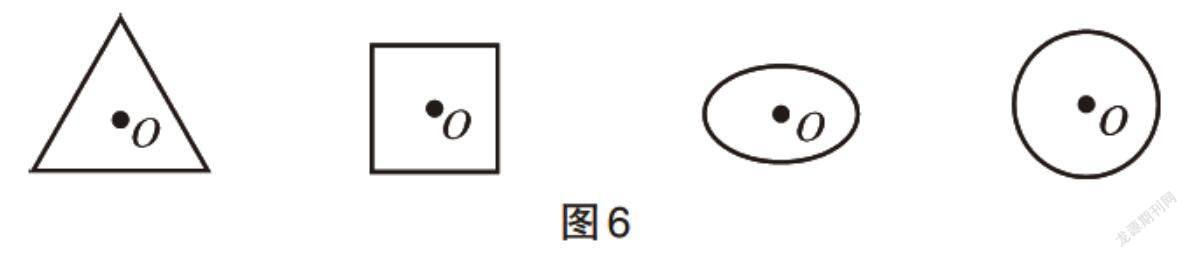
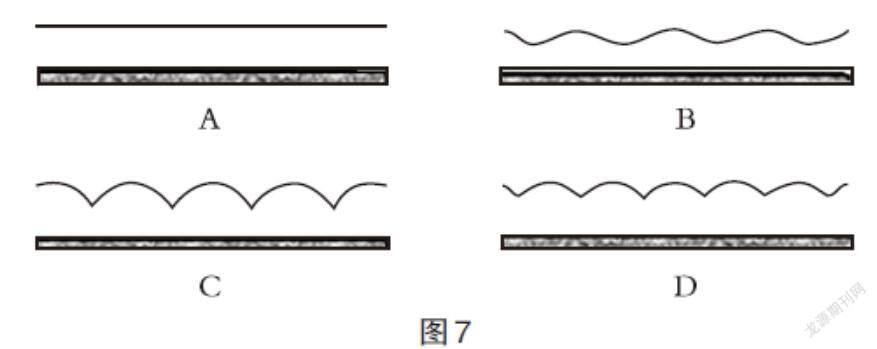
再如，为了让学生对圆的“各点均匀性”及“一中同长”特性有深刻的再认识，笔者设计了这样的题目：有以下形状不同的硬纸板（如图6），将这些硬纸板沿着一条直线滚一滚，并描出滚动过程中O点留下的痕迹。请找出下面哪一个痕迹是圆形纸板经滚动留下的。（如图7，见下页）

这道题目主要是引导学生认识和理解圆心的运动痕迹。学生通过想象不同的图形中心，在运动中出现高低变化，认识到圆心的运动痕迹是直线，圆心到滚动面的距离是与圆的半径相等，从而理解“车轮是圆的”这个现实生活中常见的数学现象。在此基础上，笔者还让学生用纸板描出一个中心点O，做出不同形状的卡片，然后固定直尺将图形进行滚动，体会各个平面图形的不同特征，从而对圆和其他平面图形之间的本质区别有了深刻的再认识。

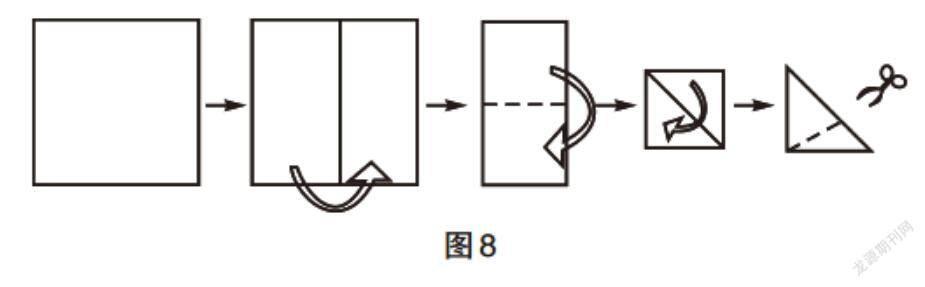
另外，为了让学生进一步理解圆的曲线研究方法，笔者设计了进阶题目：用一张正方形折叠3次，沿虚线剪出一个等腰三角形（如图8）;用一张同样大的正方形折叠4次，沿虚线剪出一个等腰三角形（如图9）。

上述两种方法，哪一种剪出来的图形更接近圆呢？借助这道题目，学生能够从中感受正多边形的边的条数越多，图形就越接近圆。由此，学生也对正多边形逼近圆的极限思想有了深刻的理解。

综上所述，教师在教学实践中通过把握圆的本质特征、设计题目，引导学生对圆展开过程性思考及深入探究，让学生对圆的本质知识学习，从“学过”真正向“学会”过渡。

【参考文献】

[1]李新.如何培育小学生“数学发现”素养[J].人民教育，2018（23）.

【作者简介】沙 欣（1989— ），女，广西玉林人，大学本科学历，二级教师，现就职于玉林市玉州区东成小学，研究方向为小学数学教学。

（责编 杨 春）