深度信念网络在建筑能耗预测领域的应用研究

侯博文，吴俊峰，陈焕新*，徐成良

（1-华中科技大学能源与动力工程学院，湖北武汉 430074；2-压缩机技术国家重点实验室（压缩机技术安徽省实验室），安徽合肥 230031）

0 引言

近年来，随着我国经济的快速发展，人民生活水平的进一步提高，全球能源消耗量逐年提升，能源短缺，资源供需不匹配等问题引起社会各界的关注，从2008—2018年，中国能源消耗总量一直呈现出上升趋势，且10年间能源消耗总量增长了44.7%。作为中国三大“耗能大户”的建筑能耗[1]，占中国社会总能源消耗量的30%～35%，能源与发展的矛盾日益突出，智慧楼宇的节能需求迫切。从能耗预测技术[2-4]在行业内的发展情况来看，基于数据驱动的能耗预测模型也是当前的主流选择。

近年来，基于数据驱动的建筑能耗预测研究越来越广泛。ZHAO等[5]从模型的复杂性、易用性和运行速度，所需投入和准确性等方面进行了比较分析。周峰等[6]采用支持向量机算法对建筑进行能耗预测和故障诊断，为建筑节能提供参考。FAN等[7]提出了一种基于数据驱动方法的通用的数据挖掘框架，阐述了数据挖掘技术在海量建筑数据中的应用前景。代德宇等[8-9]针对铜管生产过程中存在能源浪费的现象，提出了一种基于遗传算法-反向传播神经网络预测模型。曾宇柯等[10]提出了一种基于局部异常因子结合神经网络的多联机故障诊断方案，有效提高故障检测能力。19世纪40年代，多层神经网络就因其具有良好的学习特征被人们研究，但由于多层神经网络训练时会出现局部最优或者不能收敛的问题，导致多层神经网络没能得到广泛应用。直到多层神经网络的逐层训练模式的出现，使得深度学习自此开始应用于各个领域。

LI等[11]利用深度信念网络算法消除温室变量之间的相关性，提取温室中气象参数的特征，提取的特征向量被用于训练和优化LSSVM模型。GUO等[12]提出了一种基于深度学习网络的深度诊断网络建筑节能故障诊断方法，优化后的模型故障诊断正确率为97.7%，与初始模型相比，正确率提高了5.05%。郑毅等[13]基于深度信念网络算法提出了一种区域PM2.5的预测方法，对训练数据的选择和模型参数的设置进行了优化。张籍等[14]采用灰色关联度分析法建立预测模型，定量分析各因素对不同行业的影响程度，对每一种预测类型建立基于深度信念网络的中长期负荷预测模型。

1 建筑数据来源

本文的研究对象为河南省新乡市某一办公建筑中的空调系统，该建筑为政府办公建筑，水源热泵系统是该办公建筑用来制冷和供暖的主要设施，可以给室内提供良好舒适的工作环境。夏季制冷时，水源热泵机组工作原理就是将建筑物中的热量转移到水源中。

本文采用夏季居民建筑的能耗数据进行分析，获得的数据包括室内运行数据和室外气象数据，采集时间从2016-07-01的00:00至2016-08-22的13:50，由于数据的采集样本间隔均为5 min，所获得的原始数据共计15 144个数据样本，参与建模的变量分布特征见表1所示，Pt为总功率，Tsup为回水温度，qv为瞬时流量，hins为瞬时热量，Tout为室外温度，φ为相对湿度，Vw为室外风速，Il为光照强度。

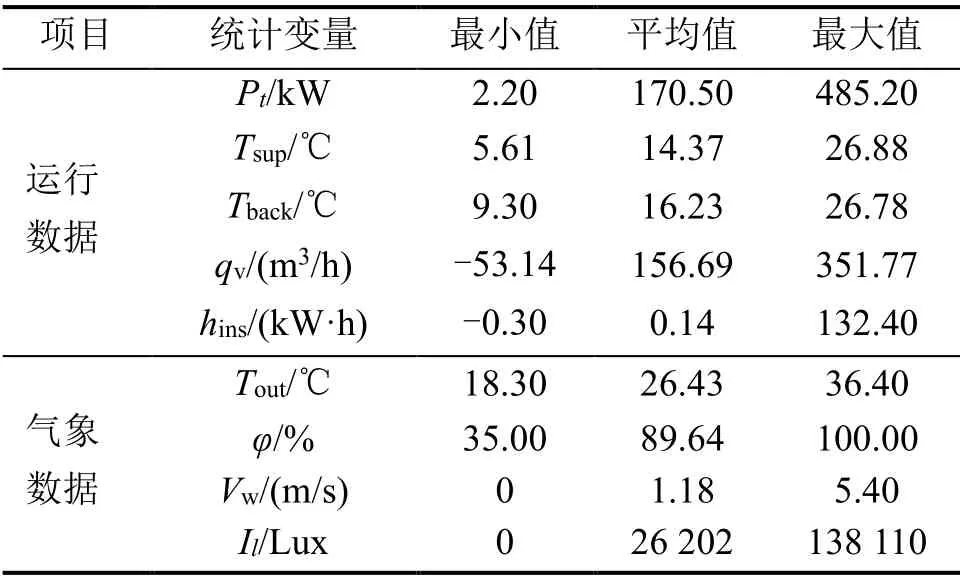
表1 参与建模变量的数据分布特征

2 深度信念网络原理及优化理论

2.1 深度信念网络

深度信念网络（Deep Belief Network，DBN）由Geoffrey Hinton提出，作为深度学习的主要算法之一，目前被广泛应用于回归预测与图像识别等领域。深度信念网络由多层受限玻尔兹曼机（Restricted Boltzmann Machines，RBM）组成，受限玻尔兹曼机采用无监督方法对模型参数进行训练，应用贪婪算法逐层优化每个隐藏层，最后结合反向微调算法对模型各层间的权值及模型阈值进行调节，使模型误差达到网络设置要求。RBM仅由两层神经元组成，一层为可视层，用于输入训练数据，另一层为隐藏层，用作特征检测器。

深度信念网络是建立在受限玻尔兹曼机的基础之上，由于单层的RBM结构只能学习到输入数据的浅层特征，将多层RBM结构叠加起来构成多层网络结构来学习数据的深层特征。深度信念网络的结构图如图1所示，由多个RBM和一个具有预测功能的顶层算法组成，顶层算法一般根据算法的实际用途来进行选择，本文选择支持向量回归（Support Vector Regression，SVR）作为预测器参与模型的构建。整个DBN的网络结构由多个RBM叠加，上一个RBM的输出作为下一个RBM的输入，相邻层与层之间采用全连接方式，层内神经单元各自独立，DBN的输入神经元个数由输入数据的变量个数决定。受限玻尔兹曼机的训练过程常采用对比散度（Contrastive Divergence，CD）算法[15]来节约模型的训练时间，其基本思想是在数据固定输入的条件下，通过调节网络参数来降低网络模型的能量值。对比散度算法采用无监督学习方法，能很好解决神经网络在模型训练陷入局部最优值的问题，有效缩短了模型的训练时间。

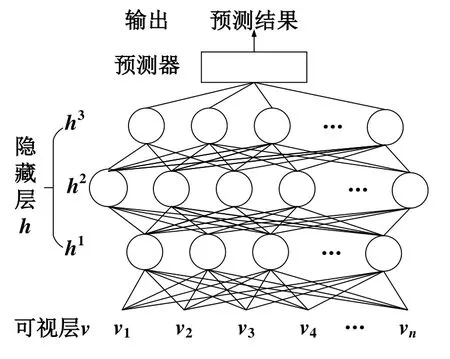
图1 DBN结构图

传统神经网络模型在层数增加过程中，存在梯度爆炸，陷入局部最优值以及训练时间过长等问题，DBN能较好解决这些问题，训练过程分为两个阶段：1）无监督的逐层预训练；2）有监督的反向微调。

2.2 布谷鸟搜索算法原理

布谷鸟搜索算法（Cuckoo Search，CS）也称杜鹃算法，是由剑桥大学的著名学者GANDOMI等[16]根据布谷鸟种群自身的寄生繁衍策略而提出的一种新型启发式算法，相比于其他优化算法，布谷鸟搜索算法具有收敛速度快、全局搜索能力强及通用性和鲁棒性好等优点。布谷鸟与其它鸟类的繁衍行为不同，布谷鸟从不哺育幼鸟，它们会特选择与自己卵形相似，产蛋和育雏的时间大致相同的鸟类作为寄主，靠巢寄生行为来繁衍后代。布谷鸟算法在模拟布谷鸟寻窝的过程中，规定以下三个理想假设：1）布谷鸟每次只下一个蛋，且根据自己的意愿选择鸟窝孵化；2）随机选择过程中，属于最优鸟窝且存有布谷鸟蛋的鸟窝会被保存；3）鸟窝总体数量不会变，布谷鸟被鸟窝主人发现的概率为Pa。

2.3 STL异常值检测法

STL（Seasonal and Trend Decomposition Using Loess）是一种经典的时间序列分解方法，由Cleveland提出，常用的数据分解模型有两种，分别是加法模型与乘法模型，如果对序列进行加法分解，其分解式[17]可以写成：

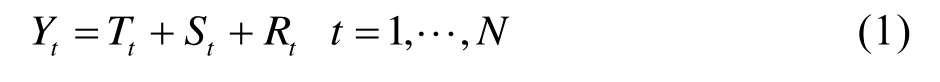
式中，Tt为趋势分量；St为周期分量；Rt为余项。

如果对序列进行乘法分解，其分解式为：

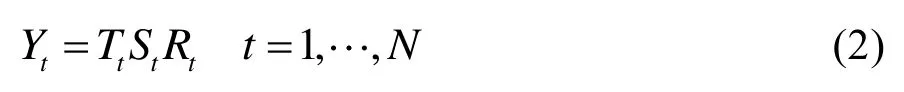
2.4 箱线图异常值检测法

箱线图又称盒须图，它既能显示数据实际分布情况，又能直观识别数据中的异常值，还可以将多组数据的分布特征显示在同一张箱线图上。箱线图中判断异常值是通过异常值截断点来判断，异常值截断点之外的数据视为异常值数据，最小值M1和最大值M2为两个截断点，计算方法见式(3)和式(4)：

上四分位数和下四分位数的差值定义为四分位距（Inter Quartile Range，IQR），计算公式为：

在水库上游设立水文站，及时提供准确、可靠的水文情报预报，为水库防洪提供切实可靠的水雨情即时资料，便于水库采取有效防洪措施。有供水任务时，可以随时了解水库水质情况。此外，还可以掌握泥沙淤积等情况。

2.5 建筑空调能耗预测模型的建立

建立基于深度信念网络的建筑空调能耗预测模型的本质是利用深度学习算法对检测到的原始数据进行分析处理，通过深度信念网络算法对输入模型的变量进行特征提取，采用支持向量回归算法作为模型的预测器，通过系统检测到的实时数据对预测模型进行训练，使得模型能通过输入检测到的数据来进行下一时刻的能耗预测。能耗预测模型的建立流程如图2所示，整个过程包括数据预处理、模型训练、模型测试以及模型评价4个部分。

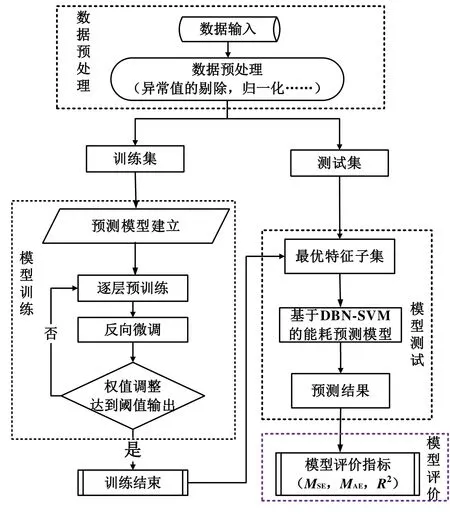
图2 能耗模型建立流程

模型评价指标有助于发现所选模型在应用过程中的实际效果，模型建立过程中，训练集中的数据用来建立模型，训练过程中未采用的测试集数据则用来判断模型的泛化性能，本文选择平均绝对误差MAE（Mean Absolute Error，MAE）、均方误差MSE（Mean Squared Error，MSE）和决定系数（R2）三个指标作为能耗预测模型的评价指标：

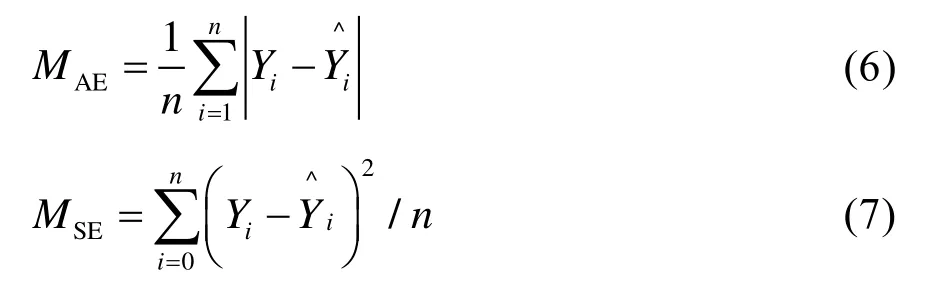
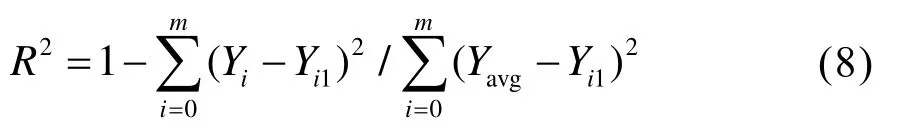
式中，n为样本数量；Yi为第i个样本的实际值；Yi1为第i个样本的预测值；Yavg为样本的平均值。

3 结果分析

3.1 异常值检测结果

对原始数据通过STL方法进行异常值检测，得到供水温度、回水温度、瞬时热量、室外温度、相对湿度、室外风速和光照强度均存在异常值，对应的异常值数量分别为409、325、155、382、259、235、317、19和1 016，由于STL分解是基于时间序列的单变量分析，所以异常值中可能存在一行数据在多个变量中均被检测为异常值。最终，通过对各个变量异常值的比较，基于STL的异常值检测共筛选出2 435个异常样本，占总体样本个数的16.1%。

同时使用箱线图方法对原始数据进行异常值检测，通过式(3)和式(4)计算可知，供水温度、回水温度、瞬时热量、室外温度、相对湿度、室外风速和光照强度均存在异常值，按照式(3)和式(4)可计算出对应异常值数量分别为682、730、48、2、386、376和149，考虑异常值中可能存在一行数据在多个变量中均被检测为异常值，通过对各样本异常值的比较，最终基于箱线图的异常值检测方法共检测出1 666个异常样本，占总样本个数的11%。

基于STL和基于箱线图的异常值检测方法分别检测出了2 435和1 666个变量，鉴于所采用的两种异常值检测方法均属于无监督学习算法，分别被STL方法和箱线图方法检测为异常值的样本也可能是正常样本[18]，因此，被STL和箱线图两种异常值检测方法同时检测为异常值的样本认定为异常样本，两种方法均认定为异常值的样本取交集，得到同时被STL和箱线图两种方法认定为异常值的样本个数为488个，占总体样本数量的3.3%。

为了不影响数据自身的统计特性，本节直接剔除数据的异常样本，共计488个异常样本被剔除，占总样本数量的3.3%。通过基于STL和箱线图两种异常值处理后，共获得14 656组数据。

3.2 建筑能耗预测模型结果

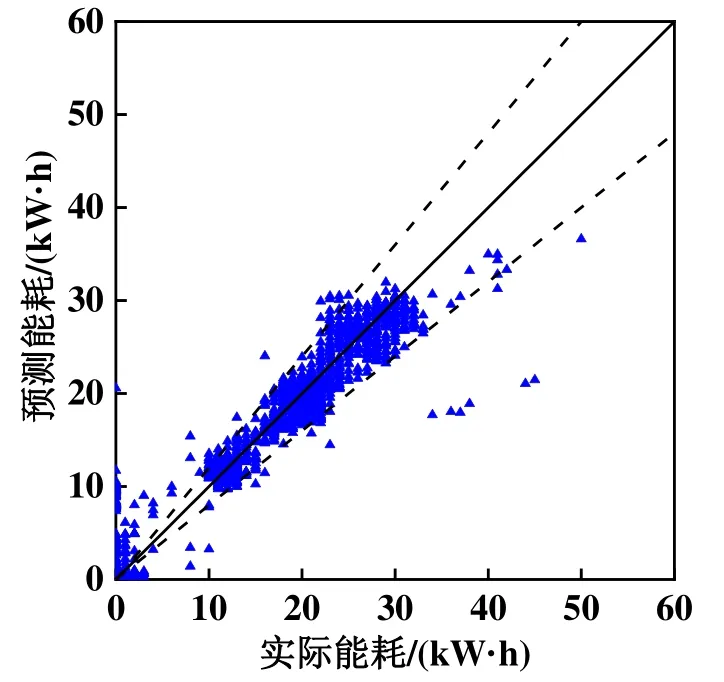
图3 基于DBN-A模型的能耗预测结果

3.3 深度信念网络模型参数的确定

为了确定隐藏层层数对模型预测结果的影响，本文设置不同的隐藏层层数来建立模型，除隐藏层层数外，隐藏层节点数均设为15个，迭代次数设置为200次，学习率设为0.01，其它网络参数均按照初始化设置，当隐藏层层数为1至5时分别计算了模型的评价指标MAE和MSE以及和初始化模型的变化情况，取5次计算结果的平均值作为最终输出，如表2所示，表中第一行为初始化隐藏层层数为2时的预测结果。

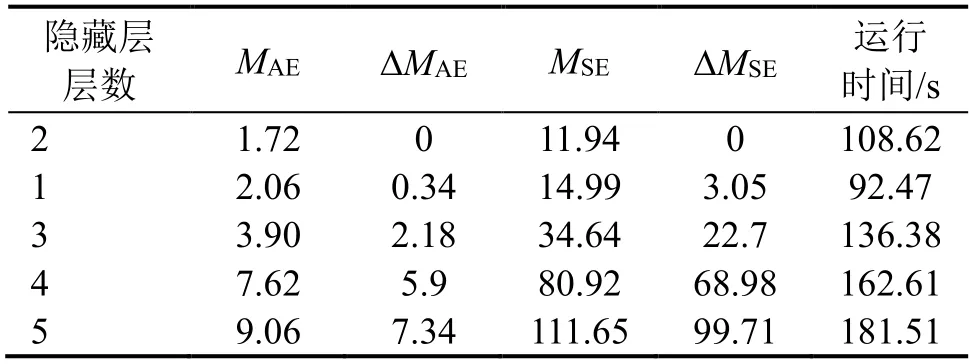
表2 基于不同隐藏层的DBN模型的误差对比

由表2可知，相对于初始化模型（隐藏层层数为2），当隐藏层层数取其它值时，ΔMAE和ΔMSE均为正值，表明此时模型误差增大，预测性能不佳，同时可以发现模型运行时间与隐藏层层数正比例相关，同时随着隐藏层层数的增加，模型训练所消耗的时间也随之增加，每增加一个隐藏层，模型训练的时间增加25 s左右。

隐藏层节点数的确定影响深度信念网络模型的预测性能，节点数选取过大或过小会导致过拟合或者欠拟合情况的发生，本文按照多种经验公式[19-21]计算隐藏层的节点数，求得各层隐藏层节点数的范围为[6, 20]，本文将隐藏层节点数设置成不同的组合来验证模型的预测性能，分别采用恒值型组合、升值型组合和降值型组合来进行隐藏层的组合，模型的迭代次数设置为200次，学习率设为0.01，分别计算模型评价指标以及模型运行时间，取5次计算结果的平均值作为最终输出，如表3所示。

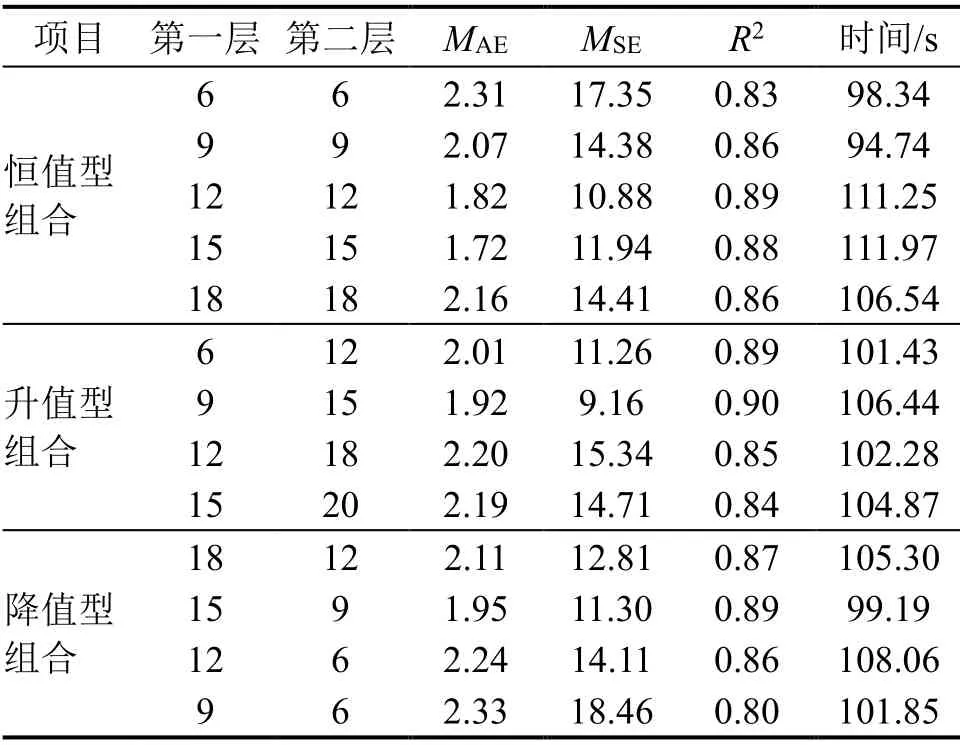
表3 不同隐藏层组合的预测结果

由表3可知，当模型隐藏层两层节点数为9和15时，获得具有最佳预测结果的建筑空调能耗预测模型，将此时模型记为DBN-B模型。

3.4 基于参数优化的建筑空调能耗预测模型优化

本文选用支持向量回归算法作为模型的预测器，核参数g和惩罚因子C对模型预测精度的影响起关键作用。本节选用布谷鸟搜索算法对模型参数进行优化。参数寻优在经过大约15次迭代后就取到了最优适应度函数值，在之后的迭代过程中，适应度函数值逐步稳定在1.059，此时深度信念网络模型的参数已得到了优化，模型中核参数g=4.59，惩罚因子C=6.61，将此时的能耗预测模型命名为CS-DBN模型。

图4所示为基于CS-DBN模型的能耗预测结果。由图4可知，预测能耗曲线较好反映了真实能耗的变化趋势，且预测值与真实值之间的误差程度减小，CS-DBN模型的MAE、MSE和R2分别为1.05，1.84和0.98，优化后的模型预测评价指标相对于未优化的DBN-B模型有较大程度提升，预测精度得到进一步的提高。

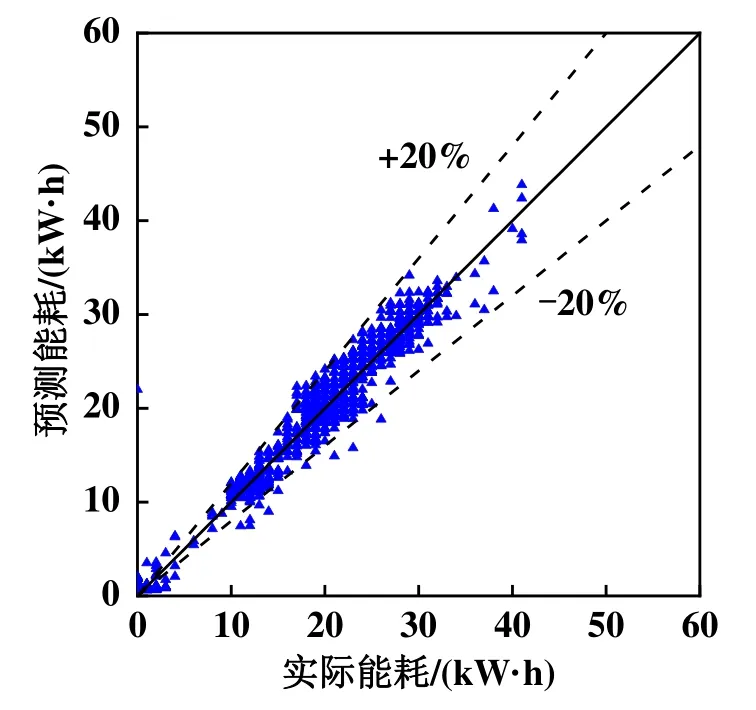
图4 基于CS-DBN模型的能耗预测结果

3.5 模型结果对比分析

本文为了获得一个最优的能耗预测模型，最大程度贴合建筑实际能耗，为建筑节能提供指导性意见。采用多种算法建立建筑空调能耗预测模型，分别建立了基于支持向量回归、极限学习机和未优化的深度信念网络建立建筑空调能耗预测模型，表4所示为各模型预测的预测结果。

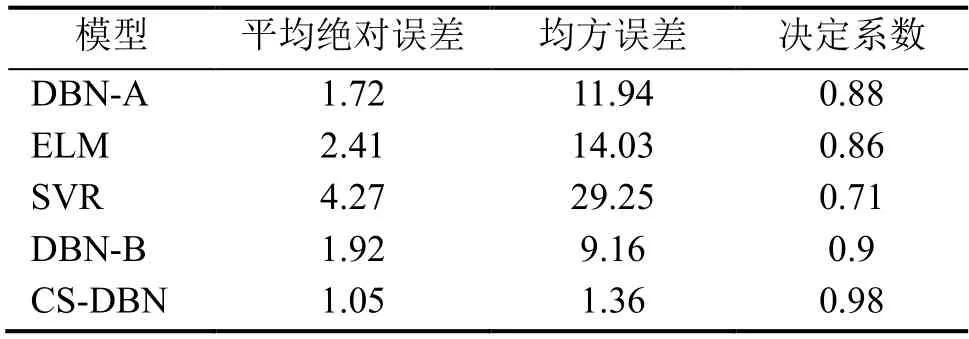
表4 各模型预测的预测结果

通过对5个模型预测性能评价指标的对比分析，在文中建立的所有能耗预测模型中，经过网络结构参数选择和布谷鸟搜索算法优化后的CS-DBN模型的MAE和MSE最小，R2最大，模型预测性能最好，相比于未进行优化的DBN-A模型，MAE由1.72减小为1.05，MSE由11.94减小为1.36，R2由0.88变为0.98，误差指标大幅度减小，拟合指标大幅度增加，能耗预测模型得到进一步的优化，可以认为经过网络结构参数选择和布谷鸟搜索算法优化后的CS-DBN模型是最佳建筑空调预测模型。

4 结论

本文通过构建基于深度信念网络算法对建筑进行能耗预测，对比了实际测量值与模型预测值，并对能耗模型进行了优化，计算了相应的模型评价指标，得到如下结论：

1）经过优化后的支模型预测性能得到改善，平均绝对误差由1.72降至1.05，均方误差由11.94降至1.36，决定系数由0.88增至0.98；

2）将预测结果与测量值进行了对比，发现用电量低于5 kW·h的数据预测能力不是很理想，分析认为是没有对开停机时的数据给予足够重视。