加工误差和形位误差对静压气浮主轴性能的影响
李瑞瑞,叶月亮,王鹏峰,李运堂
(1.中国计量大学 机电工程学院,浙江 杭州 310018;2.中国计量大学 现代科技学院,浙江 杭州 310018)
静压气浮主轴采用可压缩气体作为润滑介质实现非接触旋转运动,具有接近零摩擦、精度高、转速快、无磨损、寿命长等突出优点,广泛用于高速/超高速机床、大型镜面飞切、微电子制造等诸多领域。在静压气浮主轴制造过程中,加工刀具振动和装配精度等因素将导致转子和轴套表面存在加工误差,以及转子和轴套轴线交错产生形位误差,从而改变气膜厚度,进而影响静压气浮主轴性能。因此,研究加工误差和形位误差对静压气浮主轴性能的影响对于改善静压气浮主轴性能,设计新型静压气浮主轴结构等方面具有重要意义。近年来,许多学者研究了加工误差和形位误差对气浮主轴性能的影响[1-2]。
CUI等[3-4]利用计算流体动力学研究加工误差(轴套内波纹度、锥度、凹度和凸度)对气浮主轴静态性能的影响,采用动态网格技术定量分析加工误差与主轴运行精度之间的关系。RAJPUT等[5]认为形位误差显著影响静压气浮主轴的平均气膜厚度,导致主轴静态性能降低。YU等[6]认为部分转子表面加工误差可提升承载能力。李冰等[7]建立了轴套存在加工误差的动力学模型,研究结果表明周向加工误差对系统稳定性的影响更明显,而轴向加工误差对承载能力的提升作用更显著。WANG等[8-9]利用有限差分和线性小扰动法分析了轴向波纹、形位误差与静压气浮主轴动态性能之间的关系,结果表明动态刚度系数和动态阻尼系数随波纹幅值增大而增大,形位误差显著影响动态刚度系数,但对动态阻尼系数的影响可忽略。CAPPA等[10]分析认为主轴径向精度主要受转子加工精度的影响。ZHANG等[11]研究形位误差对静压、静压动压混合气浮主轴承载能力的影响,结果表明静压气浮主轴承载能力随形位误差的增大而减小,而混合气浮主轴则相反。SUN等[12]利用有限差分法分析了转子变形引起轴套和转子轴线交错对承载能力、高度角、气体流量和摩擦系数等参数的影响。DAL等[13]研究了主轴周向、径向形位误差与转子-轴承系统静态气膜压力分布和静态承载力之间的关系。SONG等[14]认为转子形状误差较轴套形状误差对主轴稳定影响更大。
现有文献只考虑轴承圆度、锥度和正弦波纹等加工误差对静压气浮主轴性能的影响,而对于其它周期性加工误差对气浮主轴性能的影响研究很少。本文采用有限差分法分析静压气浮主轴的静态性能。研究了加工误差(正弦波纹、矩形波纹、三角波纹)和形位误差对传统静压气浮主轴(节流孔直径相等且均匀分布)和新型气浮主轴(节流孔直径不等且非均匀分布)的承载能力的影响。给出了加工误差和形位误差的合理范围,可为静压气浮主轴的性能计算和结构优化提供参考。
1 有限差分法计算静压气浮主轴性能
1.1 静压气浮主轴结构
典型静压气浮主轴结构如图1,直径相等的两排节流孔均匀分布在轴套内。d、h、L、D、e、θ和c分别为节流孔直径、气膜厚度、轴承长度、轴承直径、偏心距、高度角和平均气膜厚度。x、y和z分别为转子周向、径向和轴向,L1为轴承边缘至节流孔间距离。外部压力气体通过节流孔进入轴承间隙形成气膜,在轴承边缘排入大气,偏心距引起气膜分布不均匀产生的气体压力差形成主轴承载能力。
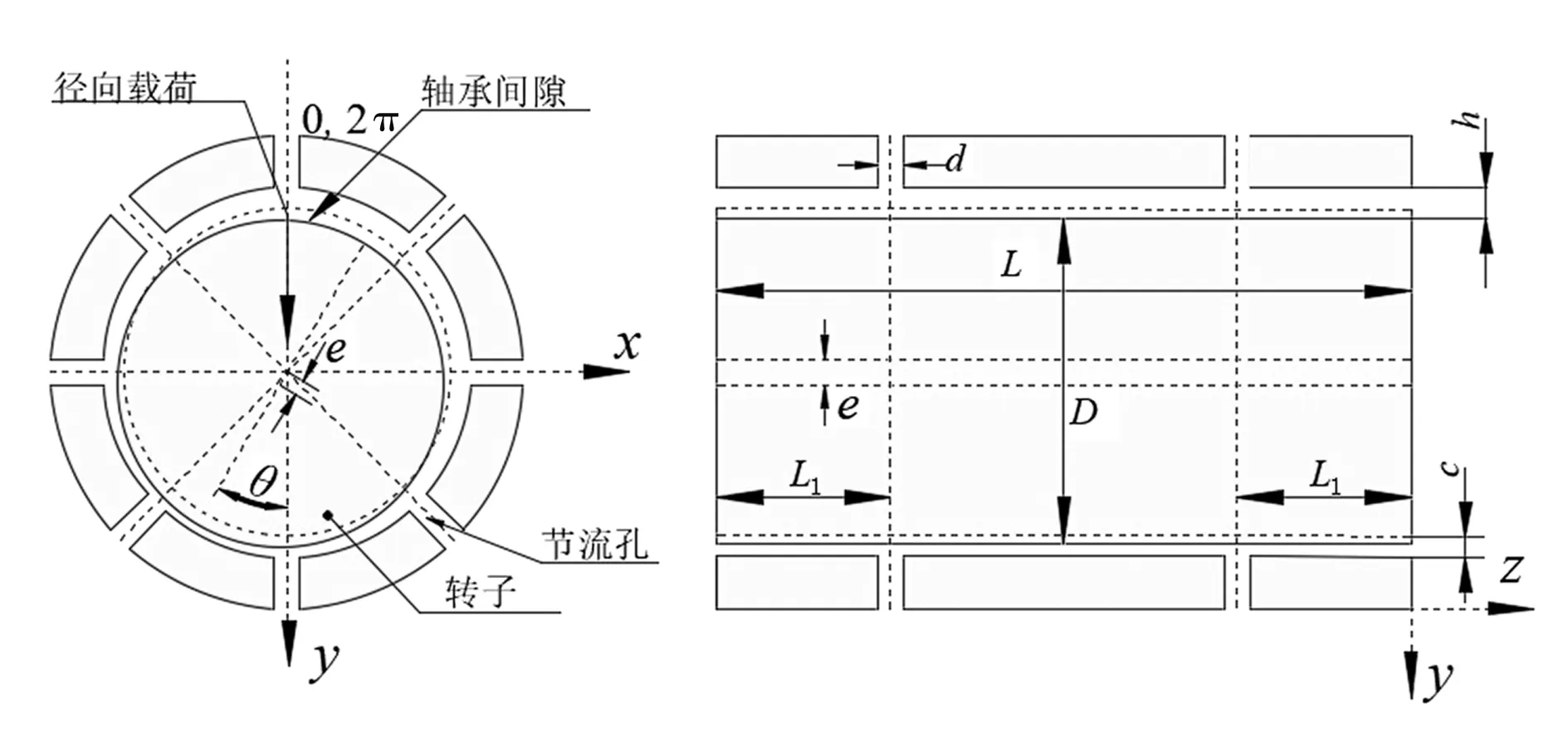
图1 典型静压气浮主轴结构Figure 1 Typically structure of aerostatic spindle
为提高性能,现提出新型静压气浮主轴结构,如图2。节流孔直径自d1至dn逐渐减小,di+1=di×γ,i=1,2,…,n-1。此外,下半部分节流孔间距减小,上半部分节流孔间距增大。节流孔i与i+1之间的夹角为αi,i=1,2,…,n-1。
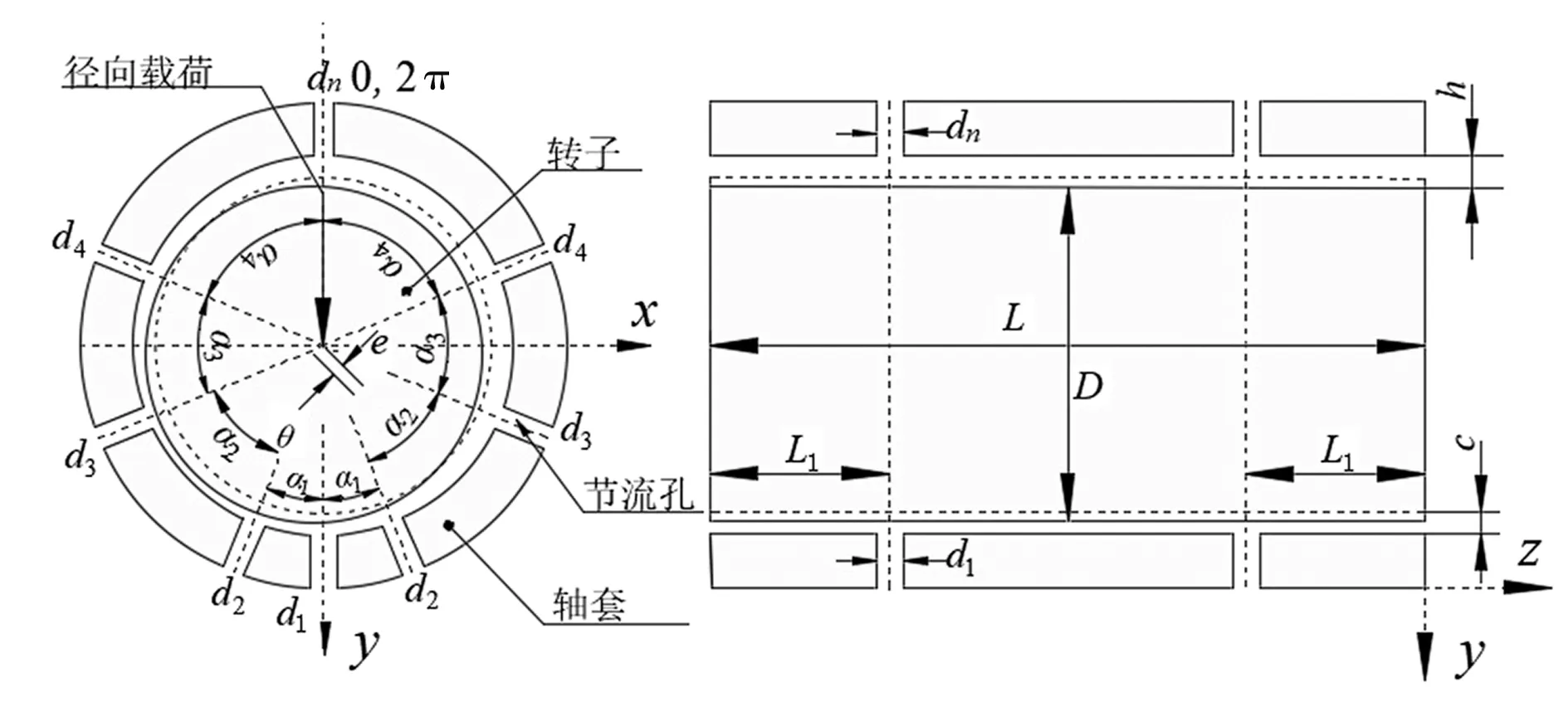
图2 新型静压气浮主轴结构Figure 2 New structure of aerostatic spindle
1.2 有限差分法计算静压气浮主轴性能
假设气体流动为等温层流,且气体黏度不变[15]。由于气膜厚度远小于转子半径,忽略转子表面曲率影响,将转子表面气膜展开成平面,在笛卡尔坐标系内建立气体运动方程、连续性方程和状态方程。得出气膜内气体流动的Reynolds方程[16-17]:
(1)
式(1)中:p为气体压力;η为气体粘性系数;u、v、w分别为气体沿x、y、z方向上的速度分量;h为气膜厚度。
h=c(1-εcos(2x/D-θ))。
(2)
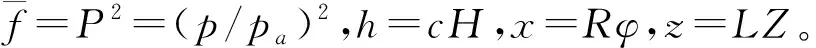
(3)
式(3)中:Λ为无量纲轴承数;Λ=(6ηωR2)/(pac2)。
假设流场达到稳定状态时气体压力为p0,气膜厚度为h0。主轴承载能力为
(4)
式(4)中:Fx和Fy分别为x和y方向上的承载能力。
(5)
(6)
采用有限差分法计算静压气浮主轴性能。忽略转子表面曲率影响,将转子表面展开成平面并划分64×20的网格。性能计算过程中的压力比、质量流量和高度角收敛条件均设置为相对误差小于10-5。网格独立性和收敛性测试表明:网格数增多,收敛精度加大,计算时间越长,而计算精度的提高可以忽略不计。
1.3 气膜厚度
加工误差和形位误差直接影响轴承间隙内的气膜厚度,进而影响气浮主轴性能,周向、轴向加工误差(正弦波纹、矩形波纹、三角波纹)和形位误差存在时气膜厚度表达式为。
正弦波纹:
hc_sin=h-Asin1sin(2πθ/Qsin1),
(7)
ha_sin=h-Asin2sin(Lz/Qsin2)。
(8)
式(7)~(8)中:Asin1、Asin2分别为周向、轴向正弦波纹幅值;Qsin1、Qsin2分别为周向、轴向正弦波纹周期。
矩形波纹:
(9)
(10)
式(9)~(10)中:Asqu1、Asqu2分别为周向、轴向矩形波纹幅值;Qsqu1、Qsqu2分别为周向、轴向矩形波纹周期。
θc=2πqs_squ1/Qsqu1,qs_squ1=0,1,…,Qsqu1-1;θa=Lqs_squ2/Qsqu2,qs_squ2=0,1,…,Qsqu2-1。
三角波纹:
(11)
(12)
式(11)~(12)中:Atri1、Atri2分别为周向、轴向矩形波纹幅值;Qtri1、Qtri2分别为周向、轴向矩形波纹周期。
θc=2πqs_tri1/Qtri1,qs_tri1=0,1,…,Qtri1-1;θa=Lqs_tri2/Qtri2,qs_tri2=0,1,…,Qtri2-1。
形位误差:
hx=h+(z-L/2)(-Ψxcosφ+Ψysinφ)。
(13)
式(13)中:Ψx、Ψy分别为转子x、y方向交错角。
图3为理想状态、存在加工误差(正弦波纹)和形位误差时的无量纲气膜厚度分布。周向正弦波纹:幅值=1 μm、周期=8,轴向正弦波纹:幅值=1 μm、周期=2,组合波纹:周向、轴向幅值=1 μm、周向周期=8、轴向周期=4;x、y方向交错角度=0.01°、x、y方向组合交错角度=0.01°。
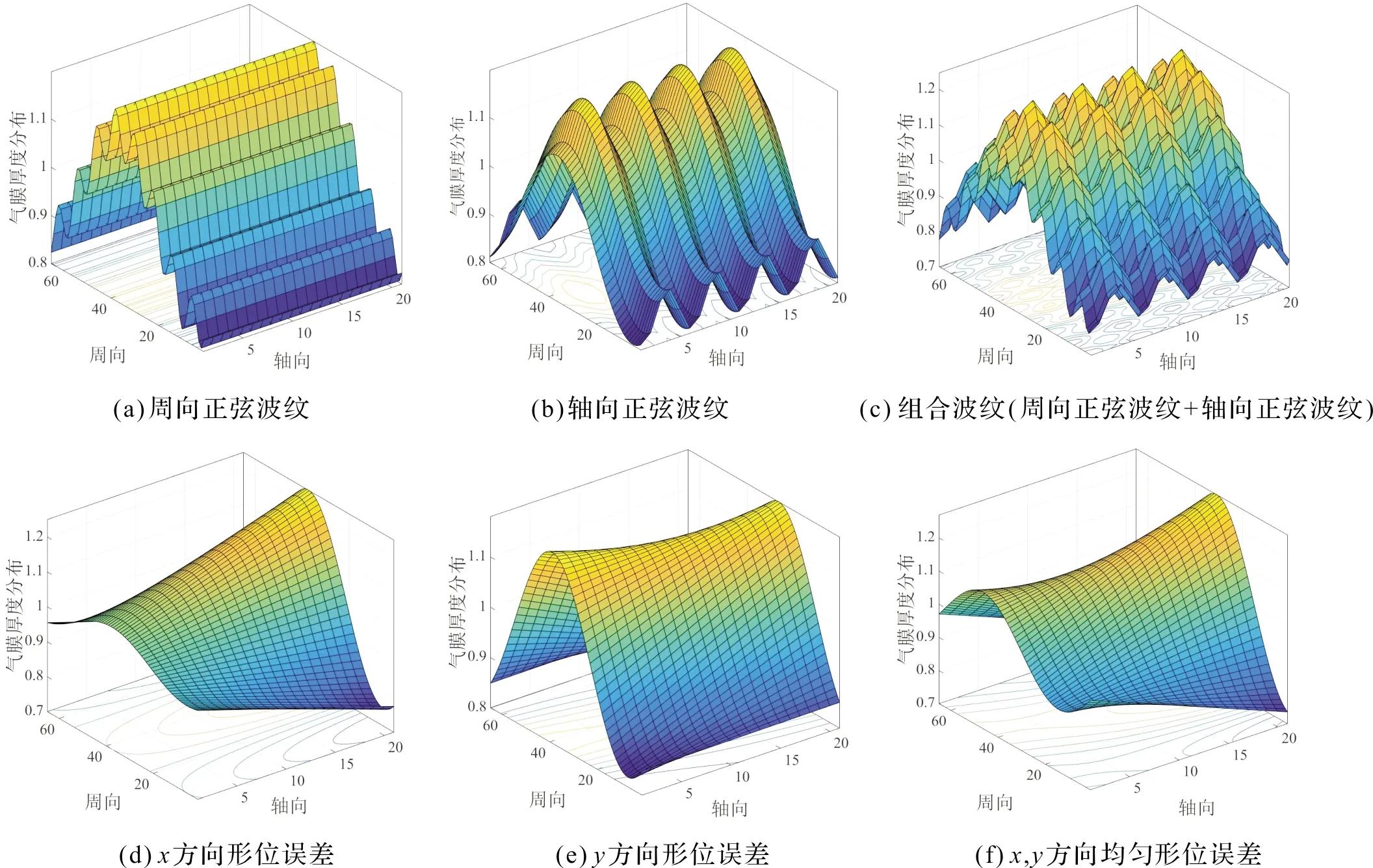
图3 主轴存在加工误差和形位误差的气膜厚度分布(ε=0.15)Figure 3 Gas film distribution of spindle with manufacturing errors and misalignment errors
2 结果和讨论
2.1 主轴参数
研究了两种静压气浮主轴结构的性能。结构Ⅰ为传统静压气浮主轴结构,节流孔直径相等且均匀分布。结构Ⅱ为新型静压气浮主轴结构,节流孔直径不相等且非均匀分布,γ取0.95,α1=π/8、α2=π/4、α3=π/8、α4=3π/8。主轴其它参数和气体特性如表1。

表1 轴承参数和气体特性Table 1 Bearing parameters and gas characteristics
2.2 有限差分法计算结果验证
为了验证本文有限差分法计算结果的准确性,采用与文献[18]相同的静压气浮主轴结构进行计算且对结果进行对比(轴承参数:ω=0 kr/m,D=100 mm,L=100 mm,c=20 μm,ps=0.5 MPa,ε=0.05),如图4。可以看出本文计算结果相对于文献18的计算结果相对误差很小。
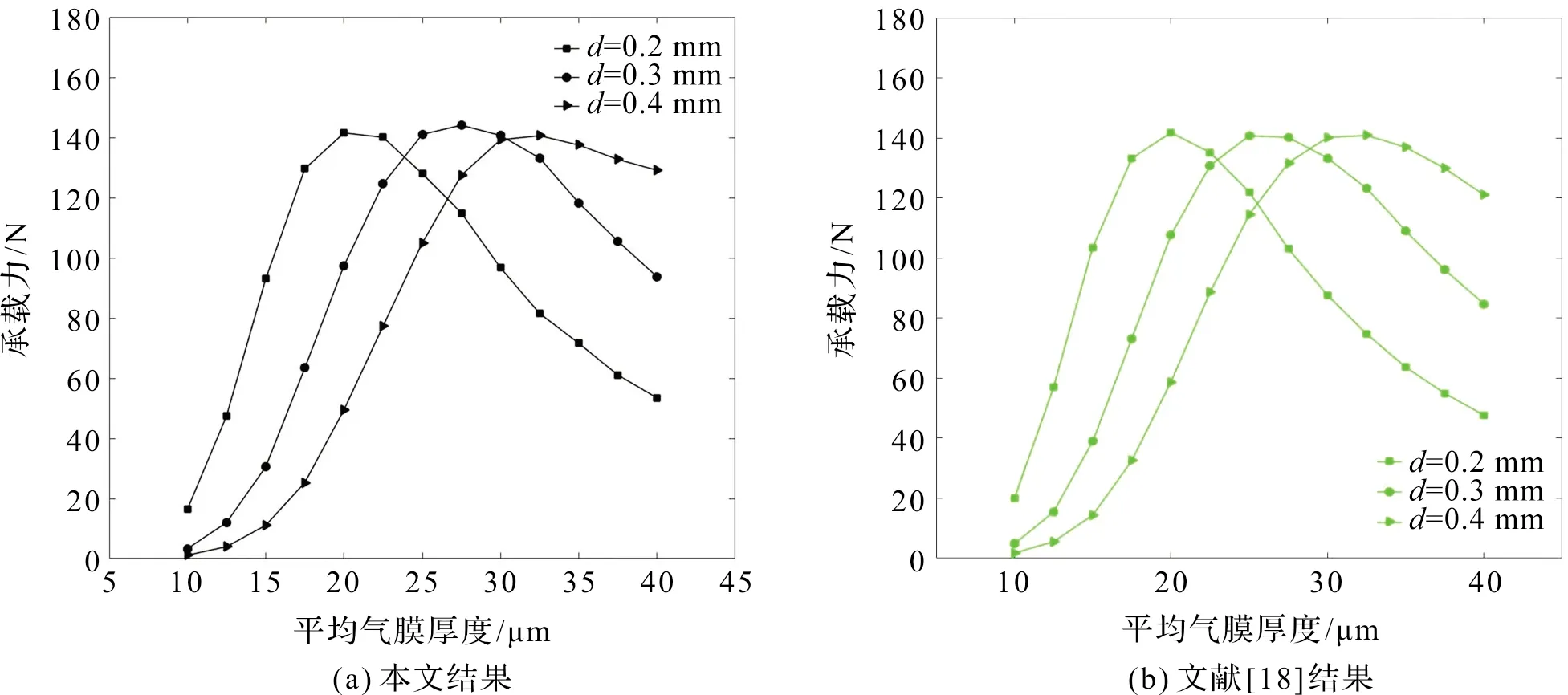
图4 计算结果与文献[18]结果对比Figure 4 Comparison of the results of present study and those of in reference [18]
2.3 加工误差对静态性能的影响
分析了轴承参数为ε=0.15、ω=10 kr/m、ps=0.5 MPa、d1=0.15 mm、c=20 μm,周向加工误差、轴向加工误差、组合加工误差的幅值、周期与承载能力的关系。加工误差幅值=幅值系数×平均气膜厚度(h)。幅值系数一般取值范围为0~0.3。本文幅值系数为0.05、0.075、0.1、0.125、0.15、0.75、0.2、0.225,对应的加工误差幅值为1 μm、1.5 μm、2 μm、2.5 μm、3 μm、3.5 μm、4 μm、4.5 μm。Q1为周向加工误差的周期,Q1=1、2、4、8。Q2为轴向加工误差的周期,Q2=1、2。
周向加工误差对两种气浮主轴承载能力的影响如图5。可以看出:加工误差周期不同,承载能力随幅值系数变化不同。加工误差周期为2、4、8时,承载能力随波纹幅值增大而增大。加工误差周期为1时,承载能力随波纹幅值增加而降低。加工误差为正弦波纹时,周期为4时承载能力最大。加工误差为矩形波纹时,周期为8时承载能力最大。
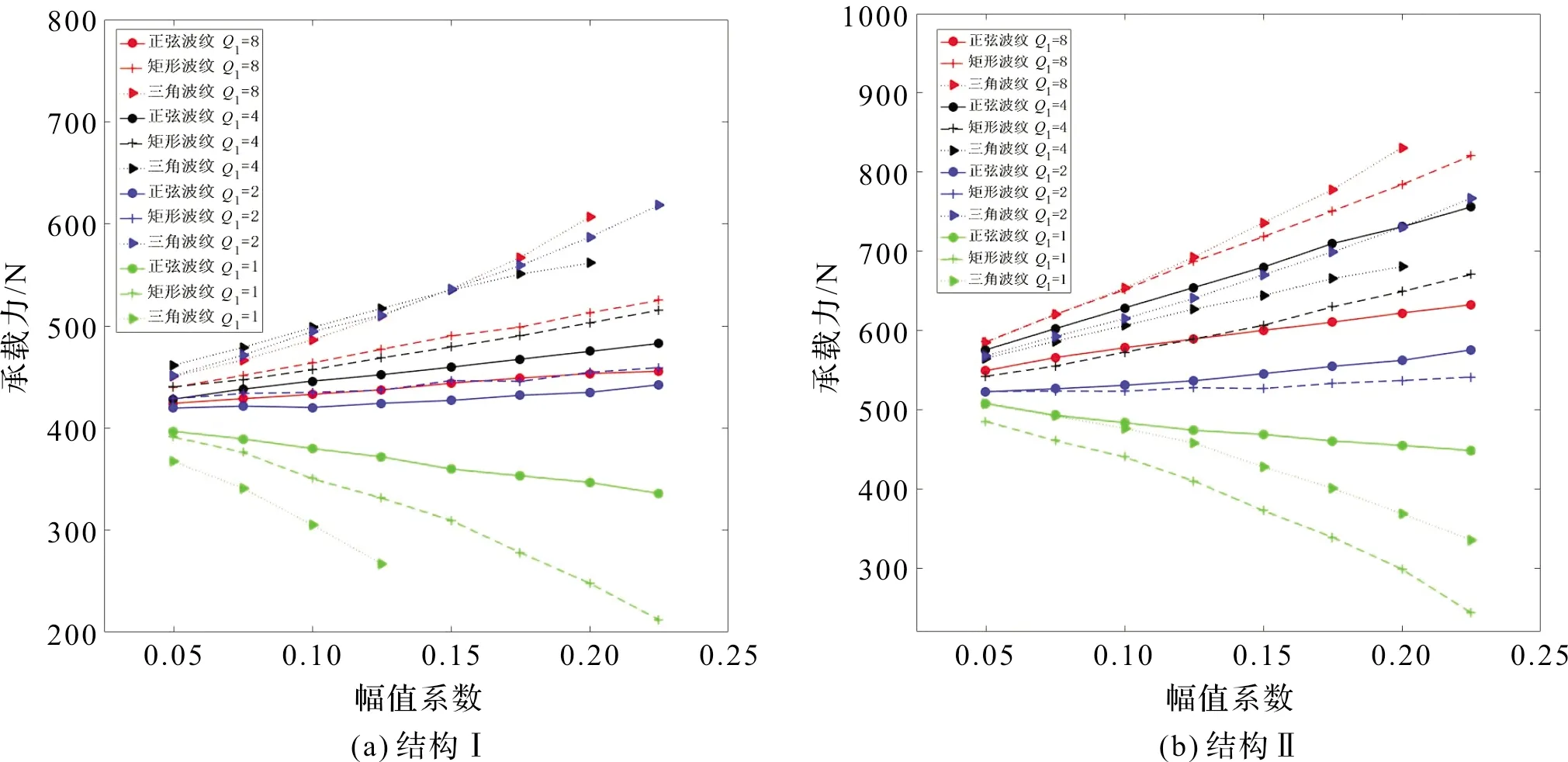
图5 周向波纹对承载能力的影响Figure 5 Effects of circumferential waviness on load capacity
图5(a)中,周期为2、4、8时,加工误差为三角波纹时承载能力最大,矩形波纹次之,正弦波纹最小。周期为1时,加工误差为正弦波纹时承载能力最大。图5(b)中,周期为8时,加工误差为三角波纹时承载能力最大,矩形波纹次之,正弦波纹最小。周期为1、2、4时,加工误差为矩形波纹时承载能力最小。
轴向加工误差对承载能力的影响如图6。可以看出:承载能力与加工误差的类型、周期、幅值密切相关。正弦波纹加工误差的周期对承载能力影响最大,三角波纹对承载能力的影响最小。周期为2时,承载能力与波纹幅值近似呈线性关系。加工误差为三角波纹时承载能力最大,矩形波纹次之,正弦波纹最小。周期为1时,承载能力随正弦波纹幅值增加而减小,矩形波纹时承载能力最大,三角波纹次之,正弦波纹最小。两种结构波纹周期与幅值相同时,结构Ⅱ的承载能力大于结构Ⅰ的承载能力。
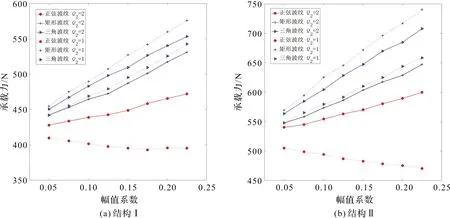
图6 轴向波纹对承载能力的影响Figure 6 Effects of axial waviness on load capacity
组合误差(周向和轴向均为正弦波纹,周向和轴向均为矩形波纹,周向和轴向均为三角波纹)对主轴静态性能的影响,如图7(周向加工误差Q1=4,轴向加工误差Q2=2)。
可以看出:承载能力与波纹幅值近似呈线性关系;波纹类型相同时,组合误差相较于周向、轴向单一差承载能力更大;波纹幅值越小,三角波纹相对于其它波纹承载能力增大越明显。三角波纹组合加工误差承载能力大于正弦波纹和矩形波纹。
2.4 形位误差对静态性能的影响
分析了轴承参数为ε=0.15、ω=10 kr/m、ps=0.5 MPa、d1=0.15 mm、c=20 μm形位误差对承载能力的影响,如图8。形位误差一般取值范围为0°~0.015°,本文取值0°~0.01°。由图8(a)可知:x、y方向形位误差增加均会导致承载能力下降。相对于x方向、y方向单独存在形位误差,x方向和y方向均存在形位误差承载能力下降幅度更大。由图8(b)可知:轴承结构的变化几乎没有改变承载能力随形位误差增大而下降的曲线斜率。在主轴存在形位误差的状态下,新型结构承载能力大于传统结构。
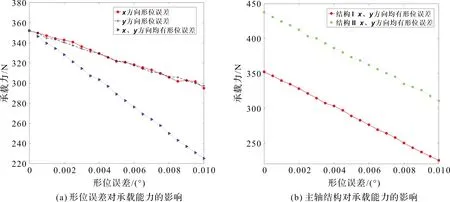
图8 形位误差和主轴结构对承载能力的影响Figure 8 Effects of misalignment errors and spindle structure on load capacity
3 结 论
本文提出了节流孔直径不同且非均匀分布的新型静压气浮主轴结构,采用有限差分法求解稳态Reynolds方程。研究了加工误差和形位误差对主轴承载能力的影响。结果表明:加工误差对气膜厚度影响显著,进而影响静压气浮主轴的静态性能。周向、轴向组合加工误差对主轴承载能力的影响大于周向、轴向单一加工误差。周向加工误差波纹周期为2、4、8,轴向加工误差波纹周期为2时对承载能力产生影响,波纹幅值越大,对承载能力的越显著。周向加工误差波纹周期为1时对承载能力产生消极影响。形位误差使主轴承载能力降低。x和y方向均存在形位误差比单方向形位误差对承载能力的影响更大。x方向的形位误差与y方向的形位误差相比,对主轴承载能力影响相差不大。与传统静压气浮主轴结构相比,新型气浮主轴可以提高承载能力。

