基于损伤力学的粉末高温合金FGH96疲劳寿命预测

徐元铭，常夏源，张书明，朱楠

（北京航空航天大学 航空科学与工程学院，北京 100191）

0 引言

涡轮盘是航空发动机的关键部件之一，承受着较高热载荷、气动载荷及振动载荷等作用，工作条件非常恶劣，直接关系到发动机的安全性、可靠性和耐久性[1]。航空发动机的发展历史显示，涡轮盘的材料运用是制约其性能和安全的关键因素[2-3]。在早期，发动机的转速较低、工作温度不高，低合金钢与铁基合金已能满足需要。随着航空发动机推重比的提高，材料强度需求增加，强化元素的大量添加以及材料合金化程度的提高成为一种发展趋势。但是，这也带来了铸锭严重偏析、压力加工成型困难等问题。随着新型粉末冶金工艺的出现及发展，制取的高温合金粉末细小，成分均匀，具有优异的力学性能和热加工性能，已成为各国制造高推重比航空发动机涡轮盘的首选材料[4]。

粉末高温合金虽然在材料性能方面有了较大提升，但是由于其特有的工艺特点，一些问题也暴露出来：原始颗粒边界碳化物沉淀（Primary particle boundary carbide precipitation，PPB）[5-7]、热诱导孔洞（Thermally induced pore，TIP）及外来非金属夹杂[8]成为粉末高温合金的三大缺陷。

目前，PPB和TIP问题已基本得到解决，粉末颗粒中的夹杂物成为影响粉末高温合金发展和应用的最主要问题。虽然通过一些制备工艺可以有效减少粉末高温合金中的夹杂物数量，降低夹杂物危害，但粉末高温合金中的非金属夹杂物不可完全去除[9]。因此，对于含夹杂物的粉末高温合金进行可靠有效的疲劳寿命预测，就显得十分重要[10-14]。

本研究基于损伤力学理论，系统地探究粉末高温合金涡轮盘寿命预测方法，并通过与实验对比，拟得出一种可靠有效的预测粉末高温合金FGH96疲劳寿命的方法和模型。本探究可以体现不同缺陷特性（含椭圆形亚表面夹杂、含椭圆形表面夹杂和含长条形亚表面夹杂）对裂纹萌生寿命影响的表征参量，通过深入分析其变化规律，建立可以直观表明粉末高温合金缺陷特性与裂纹萌生寿命之间联系的预测模型和方法。

1 模型疲劳寿命预测方法

本节介绍预测疲劳寿命的损伤力学方法、损伤演化方程与粉末高温合金裂纹萌生寿命预测方法。夹杂物周围材料裂纹萌生寿命的损伤度场D为：

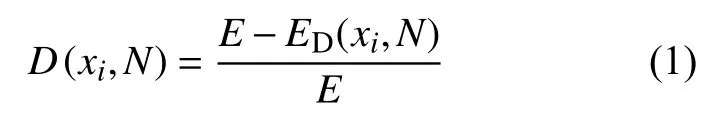
式中：E为粉末高温合金的弹性模量，ED为局部细观缺陷造成损伤后的宏观等效模量；损伤变量场D的取值范围为0~1；xi表示空间位置坐标；N为循环周次。

则材料含损伤的本构方程可以表示为：

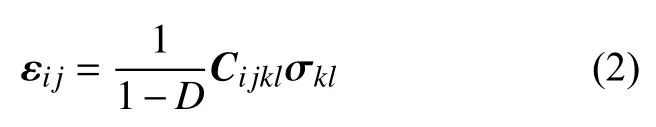
式中：εij为应变分量，σkl为应力分量，Cijkl为四阶柔度张量。

将粉末高温合金材料损伤过程视为不可逆的热力学过程，在此过程中，单位质量自由能g为：

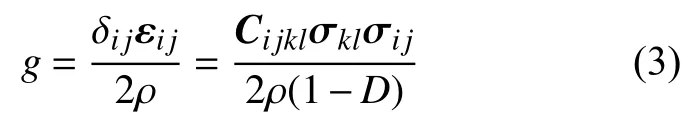
则损伤表征参量Y可表示为：

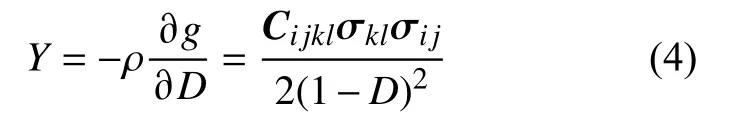
时间型的损伤演化方程可写为：

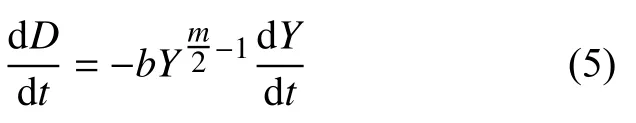
式中：m、b为损伤参数，它们是待定参数，具体数值需要根据疲劳实验数据拟合。该方程的含义是，单位时间损伤度的增量和损伤表征参量成指数函数关系，b为指数函数的系数，m是与指数相关的参数。

循环加载时有两种情况，第一种情况是在一个循环过程中表征参量只有一个峰值；第二种情况是在一个循环过程中，表征参量出现2个峰值。对于单轴拉压载荷下的疲劳问题来说，情况一对应的是拉−拉载荷，而情况二则对应的是拉−压载荷。

对于情况一，定义：

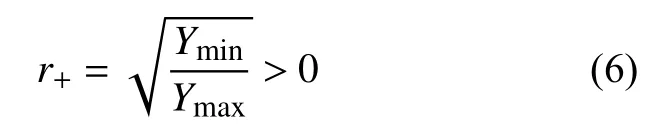
对于情况二，定义：

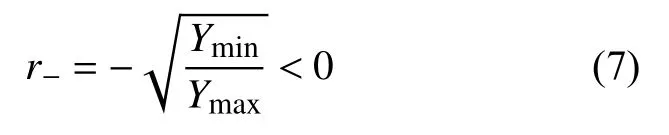
由于损伤表征参量Y和应力应变成二次关系，因此r+和r−对应单轴拉压疲劳载荷的应力比或应变比。对于以上两种情况，由式（5）可得循环型的损伤演化方程分别为：

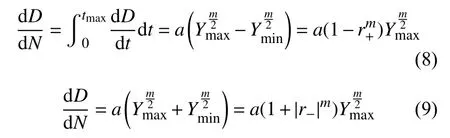
式中，a=2b/m。其含义为单位疲劳载荷循环周次造成的损伤度增量与损伤表征参量成指数函数关系，其中a为该指数关系的系数，m为指数的2倍。可见a、b和m这3个损伤参数仅有2个相互独立，在拟合参数时只需拟合其中任意2个即可。

为方便起见，将式（4）展开并写为：

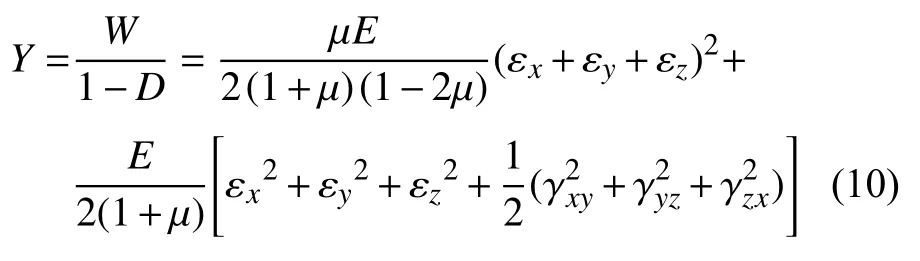
式中，W为应变能密度，μ为泊松比。

将式（10）代入式（8）、式（9）有：

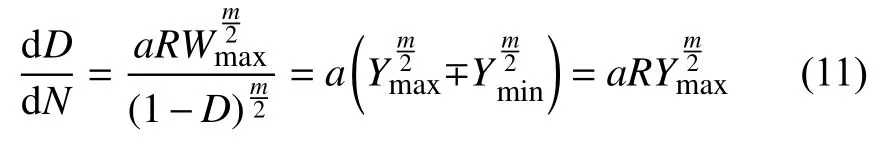
式中：“∓”在拉−拉载荷中取负号；循环特征参数R定义为：

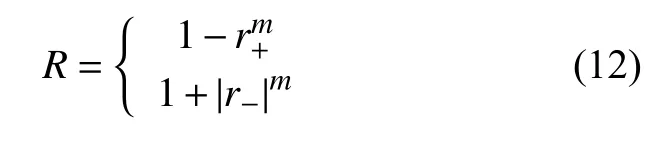
将上述损伤演化方程式（11）嵌入有限元软件进行二次开发。在有限元软件中安装实际试件的几何尺寸和材料参数建立相应的计算模型，并施加载荷边界条件。求解时逐单元计算损伤表征参量，可以得到表征参量场Y的云图，根据云图可以获得裂纹萌生位置信息。将危险点的损伤表征参量代入损伤演化方程可以计算出疲劳寿命。

下面介绍参数拟合方法和实验确定结果。

将式（10）代入式（11），简化并表达为最大循环应变的形式：

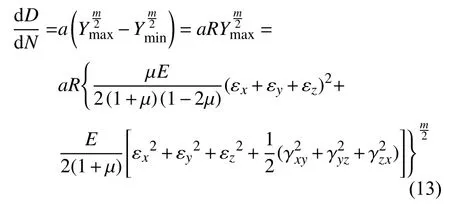
式（13）中的损伤参数a、m需要用标准光滑试件的疲劳实验数据拟合确定。各应变分量均取最大载荷时的应变分量，最小载荷的影响由循环特征因子R体现。对于无夹杂物标准光滑试件的单轴载荷疲劳试验，仅有一个应变分量，则式（13）简化为：

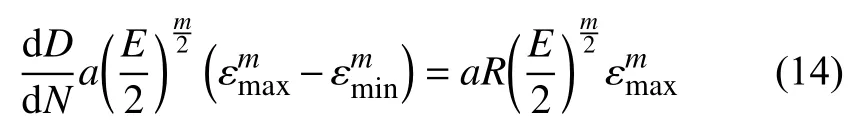
对式（14）在载荷历程上积分并取对数，可得：

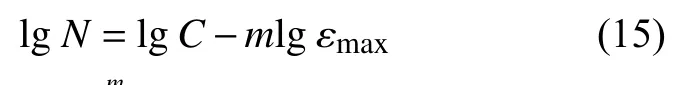
根据标准光滑试件的疲劳试验得到的不同应变水平下的疲劳寿命数据，通过线性回归就可以确定这两个参数，最小二乘法的误差函数定义为：

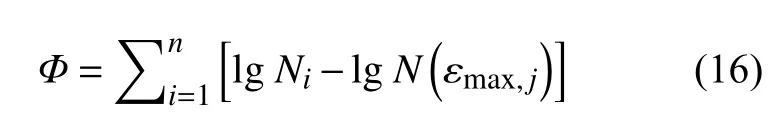
针对粉末高温合金FGH96，以530 ℃为例，使用3种应变范围下的疲劳实验数据拟合其损伤参数m、a。实验条件为单轴拉−拉载荷，控制应变加载，3种应变范围分别是0.750%、0.846%、0.950%，加载应变比r均为0.05。所有试件经过检测均为无细观缺陷的标准光滑疲劳棒件。将数据计算代入式（16）中取极小值，在对数坐标下的拟合曲线见图1。

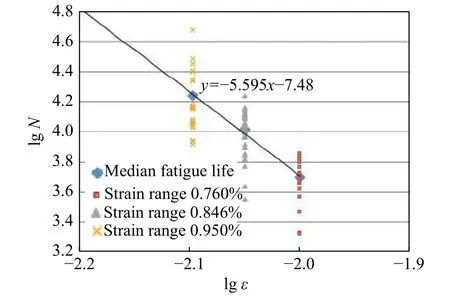
图1 530 ℃ 下 FGH96 材料损伤参数拟合曲线Fig.1 Fitting curve of FGH96 material damage parameters at 530 ℃

因此，530 ℃下FGH96合金的损伤参数由不含夹杂物的标准光滑疲劳试件的实验数据拟合确定为m=5.595，lgC=−7.48。

由式（15）可知：

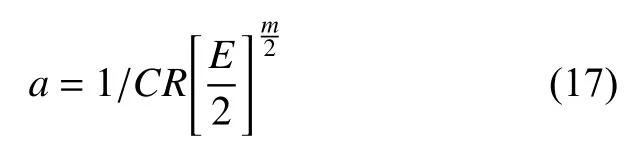
根据循环特征R的定义：

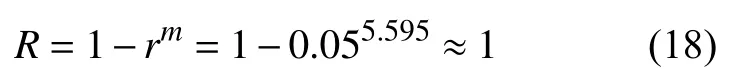
基于上述步骤，将构件在有限元软件中建立相应模型并计算其裂纹萌生寿命。具体过程包括：

1）折算载荷。根据实际疲劳载荷计算出循环中的最大名义应力或应变；简化夹杂物几何特征，按实际夹杂物几何特征简化为圆形、椭圆形或方块等形状。

2）几何建模。将待计算裂纹萌生寿命的含夹杂物构件按设计几何尺寸与材料性能在计算软件中建立相应的几何模型；划分网格，在上述方法建立的几何模型基础上划分网络。

3）边界条件施加。在上述方法划分网络的基础上将第一步折算出的最大名义应力或应变施加相应边界条件。对于一般控制位移的疲劳实验，边界条件为远场施加位移。

4）计算结果提取。在上述各方法实施后计算全场应力应变的结果，并在后处理程序中调取应变结果。

5）计算寿命结果。上述方法包括在每一计算步长内，提取全场应力应变数据并逐单元按式（10）计算表征参量Y的分布场，绘制云图判断裂纹萌生位置的危险点，再根据危险点处的表征参量值按式（11）计算疲劳寿命。

2 裂纹萌生寿命预测模型验证

对提出的预测粉末高温合金裂纹萌生寿命的损伤力学模型进行验证。在不同温度、不同载荷等实验条件下进行疲劳实验，将实验结果与本研究方法计算的裂纹萌生寿命进行对比，验证模型预测的准确性和有效性。

疲劳实验条件均为恒幅控制位移加载，使用牌号为FGH96的粉末高温合金标准光滑试件。损伤演化方程式为在寿命区间内（D=0~1）积分：

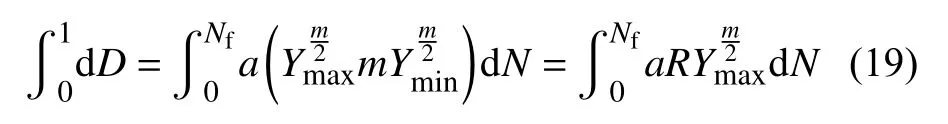
积分后把寿命Nf写在等号左侧可得：

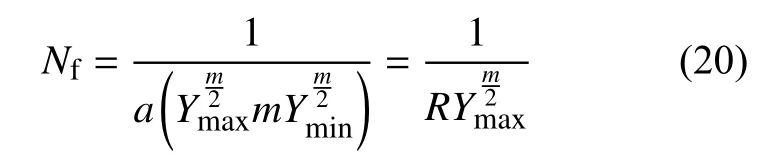
其中，循环特征因子R按式（12）计算，在应变比为0.05 时，R≈1。FGH96 在 530、600 ℃ 下的损伤参数已经由无缺陷试件实验数据拟合得到，即：530 ℃下，m=5.595，a=3.870×10−7；600 ℃ 下，m=6.282，a=9.144×10−8。一般地，载荷峰值或谷值时的表征参量Ymax、Ymin可以由有限元计算得到。因此，把具体损伤参数代入，530、600 ℃ 时，在脉动（R≈1）恒幅载荷谱下FGH96的寿命预测公式可以具体地写为位移载荷峰谷值对应的表征参量的函数形式：

对于含夹杂物情况，由于夹杂物的存在会造成局部应力应变集中，裂纹萌生危险点处的应力应变并不等于加载的名义应力应变，因此不可直接使用名义应力应变计算寿命，必须通过理论计算或数值方法得到局部应力应变场，再计算其表征参量Y的分布，最后将裂纹萌生危险点的表征参量Y最大值代入式（21）、式（22）计算其寿命。

在模型验证过程中，需根据实验使用的试件具体情况设置材料参数。若夹杂为多种成分混合型时，根据纳米压痕法测量结果，其弹性模量低于粉末高温合金基体的弹性模量，则该夹杂为软夹杂，计算时弹性模量取150 GPa，泊松比为0.3；若夹杂成分为纯金属氧化铝时，其弹性模量高于粉末高温合金基体的弹性模量，则该夹杂为硬夹杂，计算时弹性模量取400 GPa，泊松比为0.3。基体材料为FGH96，采用经典的弹塑性本构，其平均拉伸应力应变方程为：

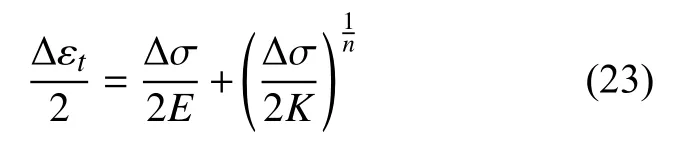
其中，弹性模量E=185.3 GPa，硬化系数K=2 702.7 MPa，硬化指数n=0.144。本构关系使用插值的方式输入10个应力应变数据点，其循环应力应变曲线如图2所示。

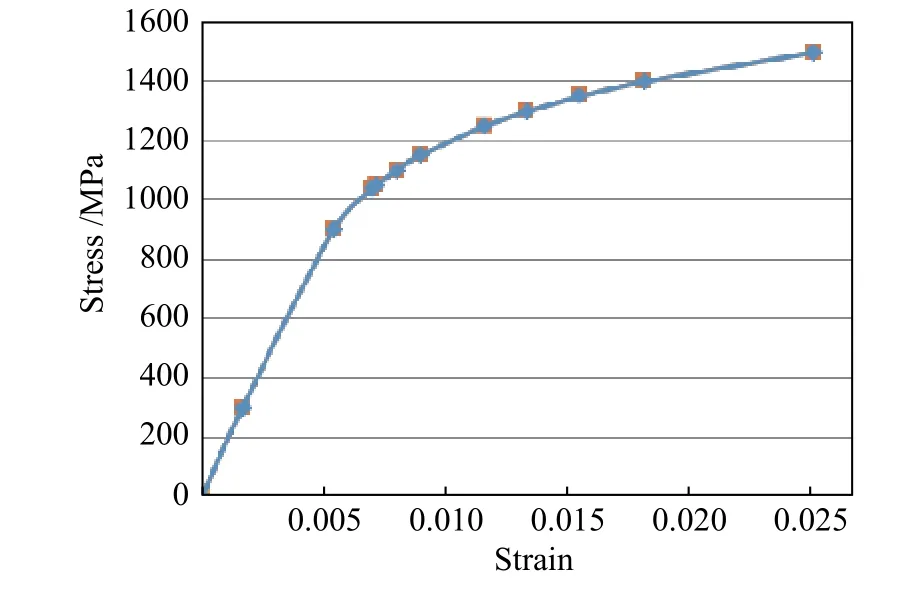
图2 FGH96 合金的循环应力−应变关系Fig.2 Cyclic stress-strain relationship of FGH96 alloy

本研究中的模型验证基于ANSYS有限元软件进行，采用PLANE82单元，具有较好的曲边几何适应性。在含夹杂物部分要对网格进行加密；施加载荷时应按照实际加载情况计算等效位移；模型的几何参数根据实际待预测试件和其夹杂物几何特征进行简化选取。大部分夹杂物可以简化为椭圆夹杂建模，其中暴露在试件表面的为表面夹杂，与表面有一定距离的为亚表面夹杂；对于表面存在较为尖锐角状轮廓的夹杂物，可以简化为长条形夹杂建模。本研究将分别说明含有椭圆形亚表面、表面夹杂的试件和长条形亚表面夹杂试件寿命预测方法和结果。

2.1 含椭圆形亚表面夹杂试件寿命预测

首先对该试件夹杂物形状和特性进行简化建模。该试件的扫描电镜图见图3，裂纹萌生处含有一个以氧化铝为主的混合夹杂物。经测量，它是一个长轴和短轴分别为63、61 μm的椭圆形夹杂。夹杂物为距离试件表面0.04 mm的亚表面夹杂。

图3 含椭圆亚表面夹杂的试件断口源区微观形貌Fig.3 Morphology of fracture source region of specimen with elliptical subsurface inclusion

有限元建模时，将夹杂物简化为一个半径为30 μm、距离试件表面0.04 mm的圆形夹杂。该夹杂成分为混合型夹杂，弹性模量为150 GPa，泊松比为0.3。试件取1/2对称模型，宽为6 mm，高为3 mm。其中，基体材料设为FGH96。模型和局部网格见图4。

图4 有限元模型网格划分Fig.4 Mesh generation of the finite element model

由于载荷为恒应变载荷，计算可知，应变范围为0.846%，应变比为0.05时，试件上下两端的最大位移为0.027 mm。在有限元模型中上表面施加位移边界条件沿y轴方向拉伸0.027 mm，在对称面上施加对称边界条件后求解。

求解后在有限元软件中进行后处理，提取每个单元的各应变分量后可按式（10）逐单元计算损伤表征参量Y值。计算出的表征参量分布见图5，其中裂纹萌生位置位于夹杂物两侧，最大表征参量为8.390。按式（21）计算其寿命为6738周次，实验结果表明该试件寿命为8125周次。

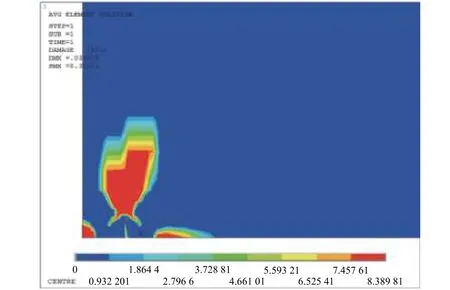
图5 试件表征参量分布Fig.5 Characteristic parameter distribution of the specimen

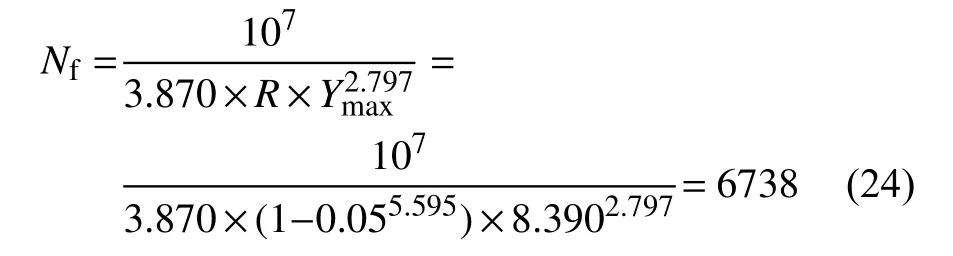
2.2 含椭圆形表面夹杂试件寿命预测

首先对该试件夹杂物形状和特性进行简化建模。该试件的扫描电镜图见图6，裂纹萌生处含有一个以Al2O3和SO2的混合夹杂物。经测量，它是一个长轴和短轴分别为102、54 μm的椭圆形表面夹杂。

图6 含椭圆形表面夹杂的试件断口源区微观形貌Fig.6 Morphology of fracture source region of specimen with elliptical surface inclusion

有限元建模时，将夹杂物简化为一个长轴和短轴分别为的102、54 μm的椭圆形表面夹杂。该夹杂成分为混合型夹杂，弹性模量为150 GPa，泊松比为0.3。试件取1/2对称模型，宽6 mm、高3 mm。其中，基体材料设为FGH96。模型和局部网格见图7。

图7 有限元模型网格划分Fig.7 Mesh generation of the finite element model

由于载荷为恒应变载荷，计算可知，应变范围为0.846%，应变比为0.05时，试件上下两端的最大位移为0.027 mm。在有限元模型中上表面施加位移边界条件沿y轴方向拉伸0.027 mm，在对称面上施加对称边界条件后求解。

求解后在有限元软件中进行后处理，提取每个单元的各应变分量后按式（10）逐单元计算损伤表征参量Y值。计算出的表征参量分布见图8，其中裂纹萌生位置位于夹杂物两侧，最大表征参量为8.686。按式（21）计算其寿命为6115周次，实验结果表明该试件寿命为6276周次。

图8 试件表征参量分布Fig.8 Characteristic parameter distribution of specimen

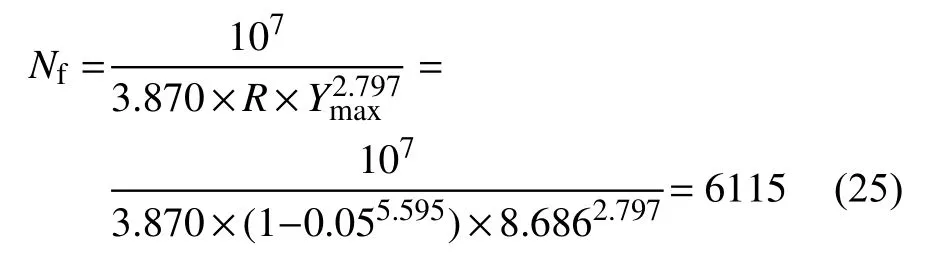
2.3 含长条形亚表面夹杂试件寿命预测

首先对该试件夹杂物形状和特性进行简化建模。该试件的扫描电镜图见图9，裂纹萌生处含有一个以Al2O3和SO2的混合夹杂物。经测量，它是一个长、宽分别为87、13 μm的长条形亚表面夹杂，距离表面深度为0.047 mm。

图9 含长条形亚表面夹杂的试件断口源区微观形貌Fig.9 Morphology of fracture source region of specimen with long strip subsurface inclusion

有限元建模时，将夹杂物简化为一个长、宽分别为87、13 μm的长条形亚表面夹杂，距离表面0.047 mm。该夹杂成分为混合型夹杂，弹性模量为150 GPa，泊松比为0.3。试件取1/2对称模型，宽 6 mm，高 3 mm。其中，基体材料设为 FGH96。模型和局部网格见图10。

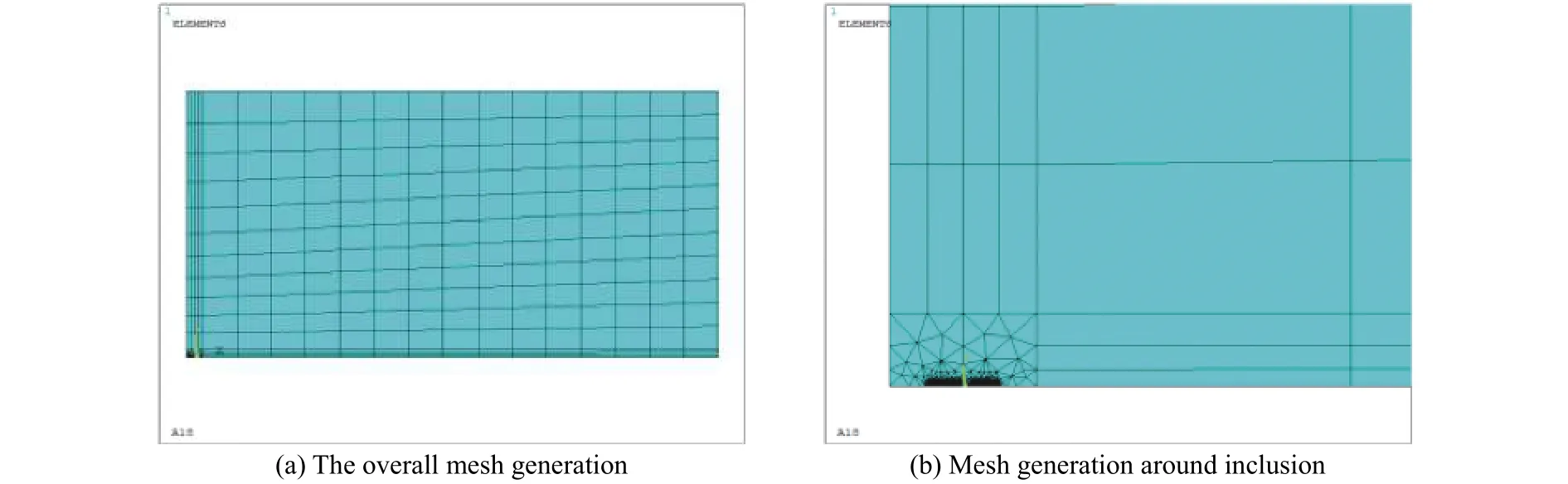
图10 有限元模型网格划分Fig.10 Mesh generation of the finite element model

由于载荷为恒应变载荷，计算可知，应变范围为0.846%，应变比为0.05时，试件上下两端的最大位移为0.027 mm。在有限元模型中上表面施加位移边界条件沿y轴方向拉伸0.027 mm，在对称面上施加对称边界条件后求解。

求解后在有限元软件中进行后处理，提取每个单元的各应变分量后可按式（10）逐单元计算损伤表征参量Y值。计算出的表征参量分布见图11，其中裂纹萌生位置位于夹杂物两侧，最大表征参量为7.810。按式（21）计算其寿命为8231周次，实验结果表明该试件寿命为11 116周次。

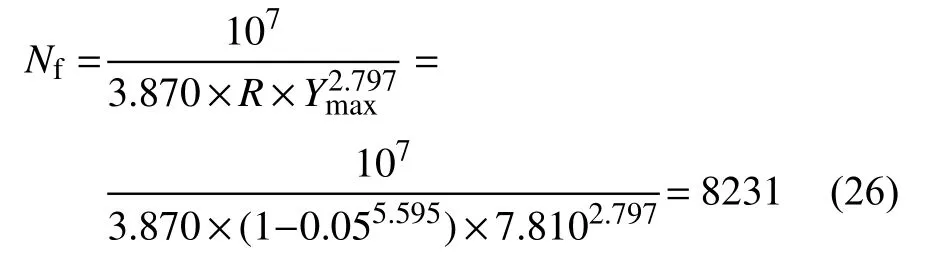
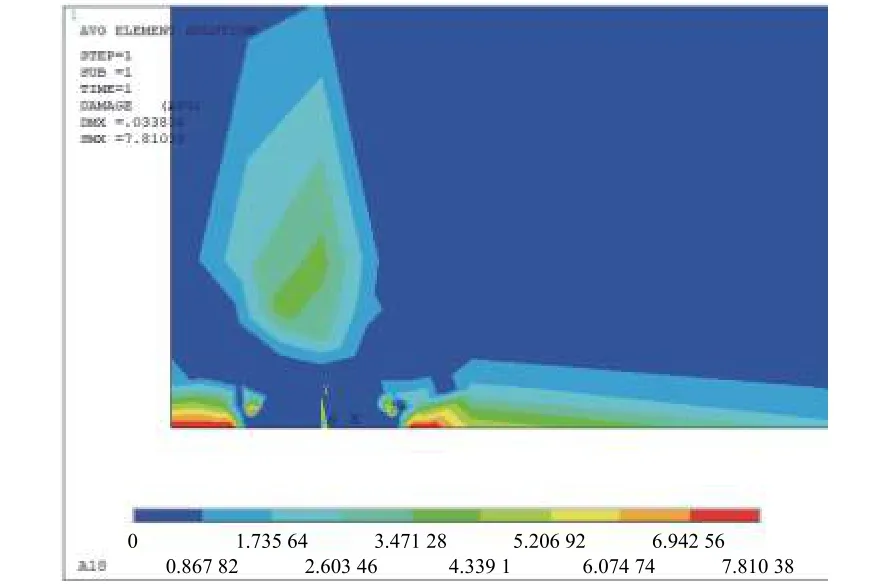
图11 试件表征参量分布Fig.11 Characteristic parameter distribution of specimen

2.4 寿命预测效果与模型评价

根据上述方法选取2组不同温度、不同应变范围（载荷）和不同应变比的含不同尺寸、位置、形状夹杂物的试件对寿命预测模型进行验证。

第1组选取5个含夹杂物试件进行寿命预测，实验条件为T=530 ℃、应变范围为0.846%、应变比r=0.05。利用寿命预测模型计算试件的理论寿命，预测结果和实验结果对比见表1。

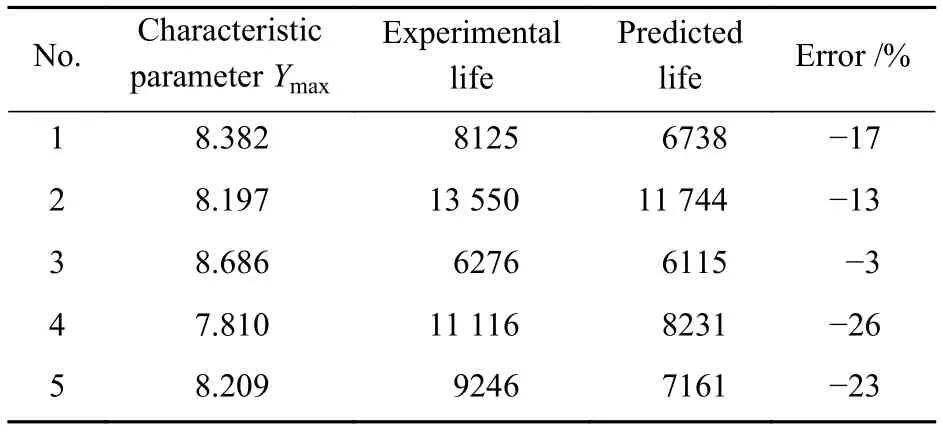
表1 第 1 组损伤力学模型预测寿命结果Table 1 Life prediction results of the first group of damage mechanics models

第2组同样选取5个含夹杂物试件进行寿命预测，实验条件为T=600 ℃、应变范围为0.752%、应变比r=0.2。利用寿命预测模型计算试件的理论寿命，预测结果和实验结果对比见表2。由于载荷为恒应变载荷，计算可知，应变范围为0.752%，应变比为0.2时，试件上下两端的最大位移为0.028 mm。该组试件直径变为5.5 mm，其余与第1组相同。

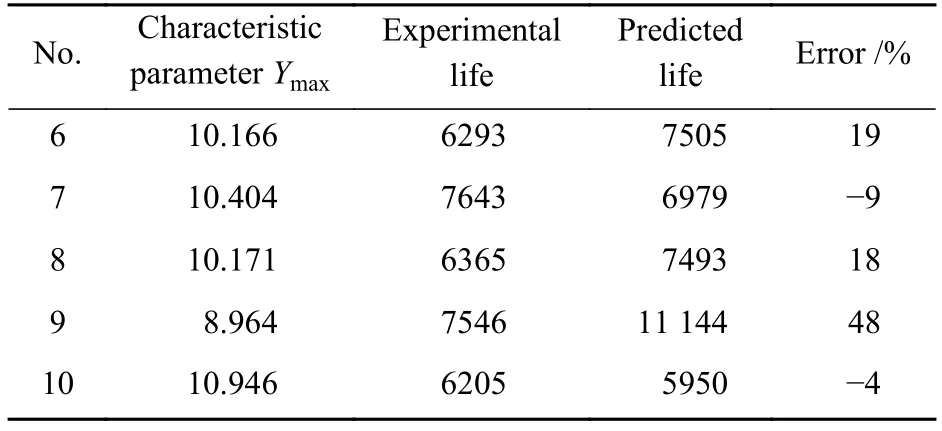
表2 第 2 组损伤力学模型预测寿命结果Table 2 Life prediction results of the second group of damage mechanics models

第3组实验条件为T=530 ℃、应变范围为0.95%、应变比r=0.05。利用寿命预测模型计算试件的理论寿命，预测结果和实验结果对比见表3。由于载荷为恒应变载荷，计算可知，应变范围为0.95%，应变比r=0.05时，试件上下两端的最大位移为 0.030 mm。

表3 第 3 组损伤力学模型预测寿命结果Table 3 Life prediction results of the third group of damage mechanics models

第4组实验条件为T=530 ℃、应变范围为0.76%、应变比r=0.05。利用寿命预测模型计算试件的理论寿命，预测结果和实验结果对比见表4。由于载荷为恒应变载荷，计算可知，应变范围为0.76%，应变比r=0.05时，试件上下两端的最大位移为 0.024 mm。

表4 第 4 组损伤力学模型预测寿命结果Table 4 Life prediction results of the fourth group of damage mechanics models

以上4组含夹杂物试件的理论模型预测结果较好地反映了夹杂物对粉末高温合金疲劳寿命的影响规律。预测结果与试验结果基本吻合。而且，模型参数适用于不同温度、应变比载荷的情况。模型的局限性在于，该模型是二维模型，不能完全反映三维构件特征。其中，对于2个特征长度差别较大的试件（若夹杂物为椭圆，则指离心率较大；若夹杂物为多边形或长条，则指长宽比较大）可能会造成一定误差。这是由于，夹杂物的两个方向特征长度均为断口测量结果，而对寿命影响大的因素是断口面内的夹杂物尺寸与试件轴向夹杂物长度之比，也就是长高比或宽高比，而非长宽比。建立有限元计算模型时，沿试件轴向（加载方向）的夹杂物尺寸是未知的，只能用断口面内的长宽比代替宽高比或长高比进行计算。当这个比值接近1时，对寿命预测的影响较小，而当这个比值较大时，对寿命预测影响较大。因此，建议在工程预测中，尽量用3D扫描得到夹杂物的三维尺寸模型；若无法得到轴向数据，建议用圆球型模型预测。

3 结构模拟件寿命计算

在寿命预测模型的实际应用中，需要对粉末高温合金FGH96结构件进行计算。通过对涡轮盘结构模拟件的计算，进一步说明粉末高温合金结构件的裂纹萌生寿命计算方法的可靠性。

3.1 模拟件几何尺寸

模拟件为一变厚度板件，长度为80 mm，宽度为 40 mm，加载区域厚度为 6 mm，断裂区域厚度为4 mm。断裂区域含有2个直径为10 mm的孔洞。断裂后的实验件如图12所示。

图12 模拟件实验断裂图Fig.12 Experimental fracture photo of simulated part

3.2 实验条件与载荷

实验温度为(600±10) ℃。采用控制载荷方式加载，实验载荷分为 A 组：“1400−25 000−1400 N”（实验段最大和最小名义应力为 781、43 MPa）；B 组：“800−29 960−800 N”（实验段最大和最小名义应力为936、25 MPa）。载荷循环至断裂，记录循环周次。16个模拟件疲劳实验参数和寿命统计见表5。

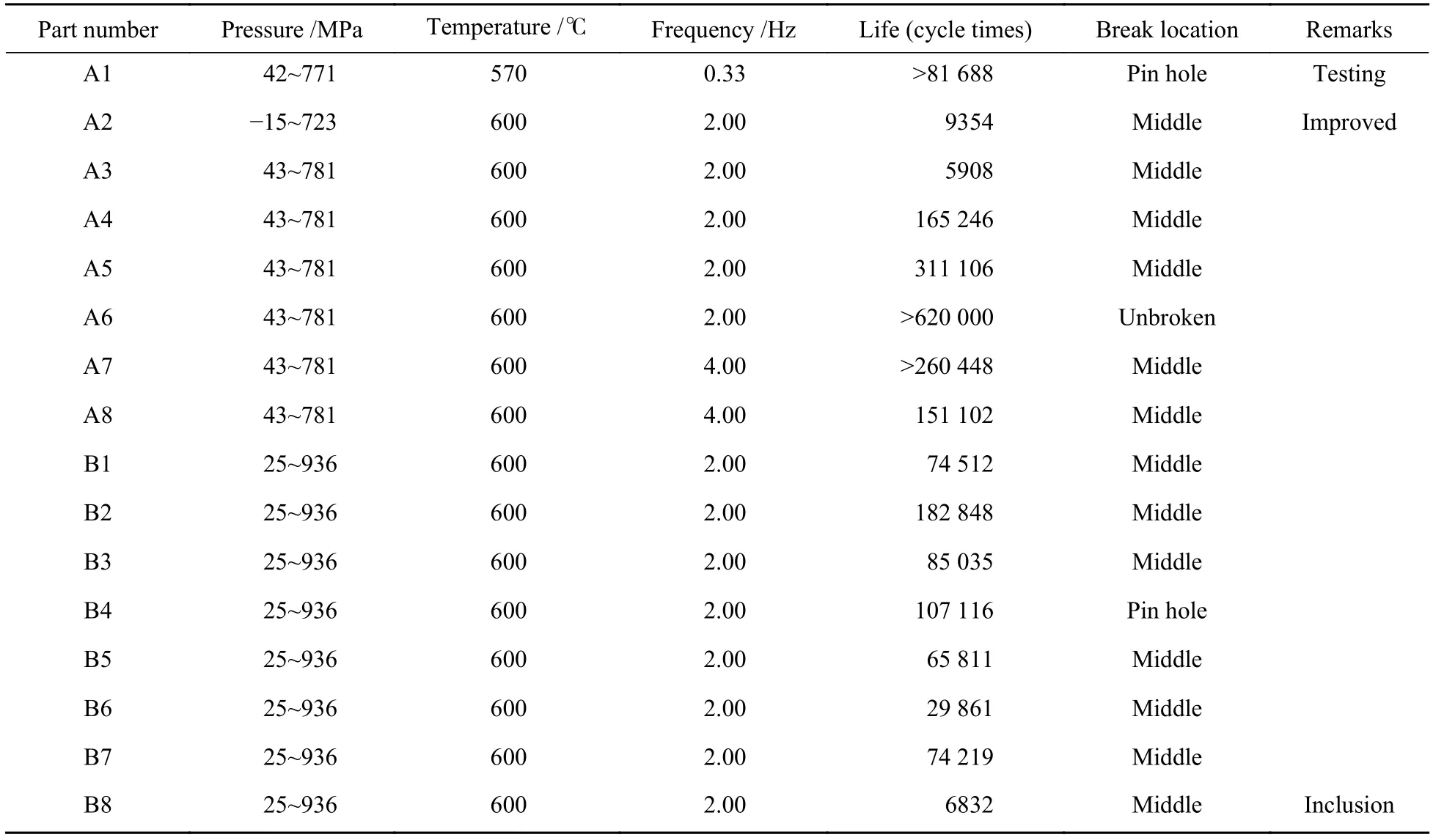
表5 模拟件疲劳实验参数及寿命统计Table 5 Fatigue test parameters and life statistics of simulated parts

3.3 寿命计算

由于实验加载方式为控制载荷方式，在600 ℃时，宜采用式（22）进行裂纹萌生寿命计算。

此时，需要分别计算载荷峰值和谷值时对应的表征参量Ymax和Ymin，然后将其代入式（22）计算裂纹萌生寿命。由于加载方式为控制力法，表征参量计算宜采用应力方式：

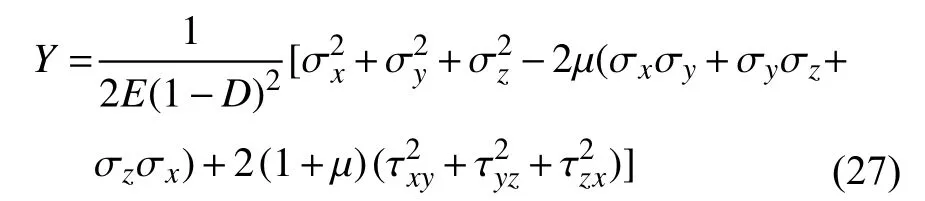
3.4 平均寿命计算

为得到载荷峰谷值时对应的损伤表征参量，利用有限元进行计算。根据试件的对称性，可选取1/8模型建立计算模型。材料参数均采用FGH96的循环应力应变关系进行弹塑性分析。计算单元采用三维实体单元SOLID186。网格划分在试验段孔边加密，网格划分形式见图13。对于此1/8模型有3个对称面，加载时应在此3个面设置对称边界条件。A组在远场分别施加峰谷载荷25 000、1400 N；B 组在远场分别施加峰谷载荷29 960、800 N。

图13 模拟件的有限元网格Fig.13 Finite element mesh of the simulated part

计算完后，分别提取载荷峰谷值时各单元应变分量计算表征参量Y并绘制云图（图14、图15）。由图可见，在宏观尺度上裂纹萌生危险位置位于中间试验段孔边应力集中位置，表明有限元计算结果与实验观测结果一致，证明计算方法的准确性。

图14 A 组载荷表征参量分布Fig.14 Characteristic parameter distribution of load of group A

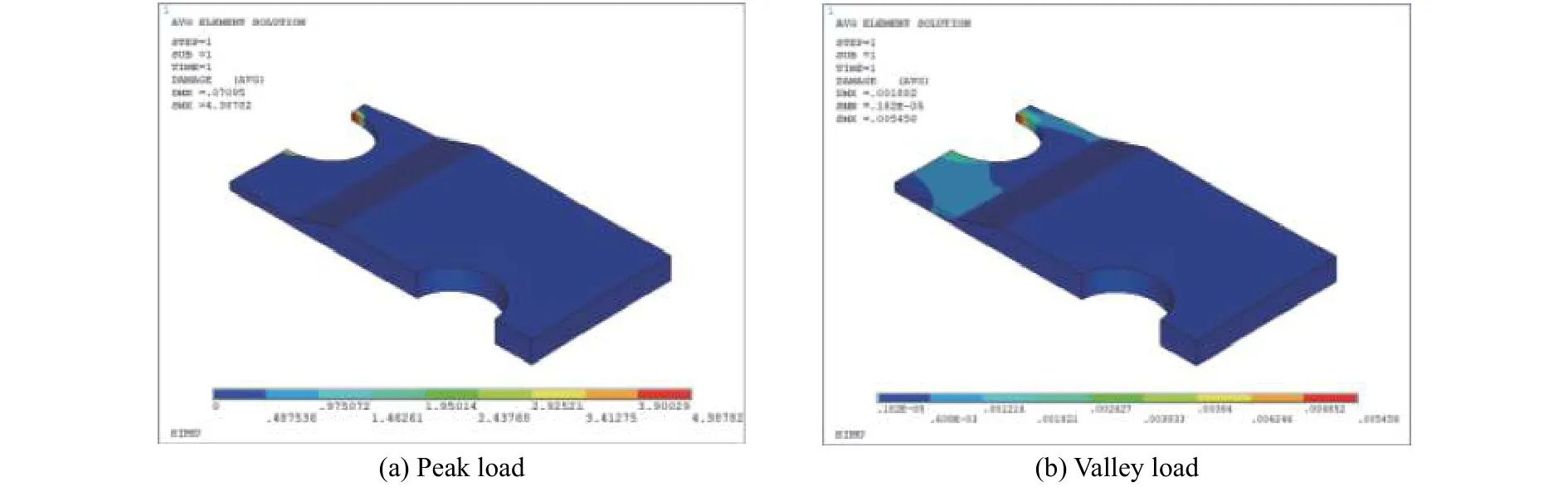
图15 B 组载荷表征参量分布Fig.15 Characteristic parameter distribution of load of group B

A组峰值载荷对应的危险点表征参量为Ymax=3.645，谷值载荷对应的危险点表征参量为Ymin=0.017，将它们代入式（22），得到模拟件的平均裂纹萌生寿命为188 239周次；B组峰值载荷对应的危险点表征参量为Ymax=4.388，谷值载荷对应的危险点表征参量为Ymin=0.006，将它们代入式（22），得到模拟件的平均裂纹萌生寿命为105 089周次。

通过与表5中的疲劳寿命实验数据对比可得，采用本研究所建立的疲劳寿命预测模型所计算出来的疲劳寿命相比较于实验数据更低，寿命值偏于保守，这证明所建立的疲劳寿命预测模型是可靠的。

4 结论

1）基于损伤力学的热力学理论，定义表征材料疲劳失效的损伤参量Y，并给出其计算方法。计算结果表明，损伤参量Y能较好地表征材料的低周疲劳损伤，同时它既适用于无夹杂物试件，也适用于含有夹杂物的试件。

2）建立的粉末合金FGH96疲劳寿命预测模型，适用于不同的温度、不同应变范围及不同的应变比实验条件。对于无夹杂的试件，疲劳寿命误差在12%以内。表明温度、应变范围和应变比对粉末合金FGH96的疲劳寿命预测影响不大。

3）该模型是二维模型，对于特征长度差别较大的试件可能会造成一定误差。建立有限元计算模型时，沿试件轴向（加载方向）的夹杂物尺寸是未知的，只能用断口面内的长宽比代替宽高比或长高比进行计算。当这个比值接近1时，对寿命预测的影响较小，而当这个比值较大时，对寿命预测影响较大。