动态连续下降进近路径生成与优化研究

宫峰勋，高松松

（中国民航大学电子信息与自动化学院，天津 300300）

连续下降进近（CDA，continuous descending approach）能够改善民航运输效益低、环保差的不利形势[1-3]。由于管制员无法精确地预测飞机的下降位置，难以很好地控制安全间隔，目前CDA 运行只能在低流量空域中实现，限制了CDA 技术的广泛应用[4-5]。Stell[6]采用多项式逼近算法快速估算CDA 路径中下降顶点（TOD，top of descent）的位置，经验证求得误差不超过5 n mile。Alam 等[7]在CDA 基础上提出动态CDA 概念进行路径的横向和纵向优化。文献[8-9]提出航迹分段优化方法，用微积分思想完成子航段的最优控制优化，从而实现CDA 路径规划。Tian 等[10]设计了CDA 影响参数的性能分析软件，成功获取飞机性能参数。苑克剑[11]采用Gauss 伪谱算法实现CDA 飞行航迹的分段优化，建立基于融合点的CDA 运行程序，用时间决策算法优化CDA 飞行方式。结合CDA 运行原理与四维航迹预测技术，文献[12-13]提出最优时间CDA 算法，与传统阶梯式下降路径相比，优化的CDA 路径在下降的水平距离和运行时间方面都具有明显优势。

综上所述，CDA 运行方式在减少噪声、降低燃油量、缩短下降时间等方面都具有一定优势，但目前并未实现既高效又安全的CDA 运行路径规划。针对以上问题，基于CDA 受力平衡状态分析，结合飞机下降数据和下降速度剖面构建动态CDA 路径生成模型。在划分水平、垂直安全间隔的基础上，完成CDA 路径的空间呈现与分析，构建基于某一高度层的路径范围筛选模型，通过筛选路径点方式完成CDA 的路径筛选，并进行下降转弯角度限制、飞机受力平衡状态约束和最短航段距离规定，求得最优CDA 路径，实现安全、高效的CDA 运行路径规划。

1 动态CDA 建模分析

1.1 动态CDA 路径生成模型

动态CDA 是根据不同巡航高度，按照CDA 进近方式选择不同TOD 对应的下降路径实施下降。将飞机巡航高度、可行加速度作为实时变量，在牛顿第二定律和CDA 受力平衡分析的基础上，结合飞机速度下降剖面构建动态CDA 路径生成模型。文献[14]规定，飞机到达起始进近定位（IAF，initial approach fix）点时的速度不超过250 kt（1 kt=1.852 km/h），IAF 点的高度为3 000 m，将飞机下降过程分为从TOD 点到IAF 点及IAF 点到最后进近定位（FAF，final approach fix）点的匀减速下降运动，飞机下降速度剖面如图1所示。

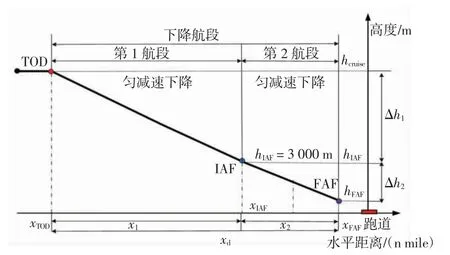
图1 飞机下降速度剖面Fig.1 Profile of the aircraft descent velocity

图1中：hcruise、hIAF、hFAF分别为巡航高度、IAF 点高度和FAF 点高度；xTOD、xIAF、xFAF分别为TOD 点、IAF 点和FAF 点与机场跑道的水平距离；x1、x2、xd分别为第1、第2 及整个下降航段对应的水平距离；Δh1，Δh2分别为第1 航段和第2 航段对应的下降高度。

第1 航段与第2 航段的下降时间分别表示为

式中vIAF、vFAF分别为IAF 点、FAF 点的下降速度。第1航段与第2 航段下降的航段长度分别表示为

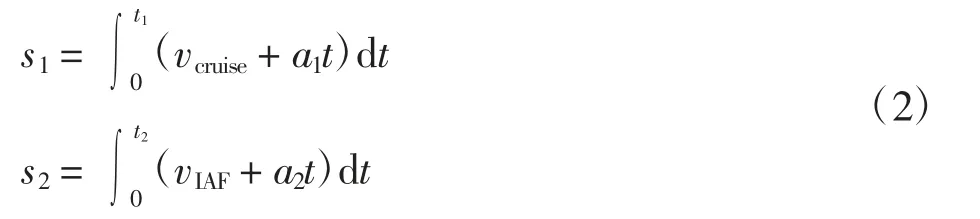
第1 航段与第2 航段下降的水平距离分别表示为

综上所述，CDA 路径生成模型表示为

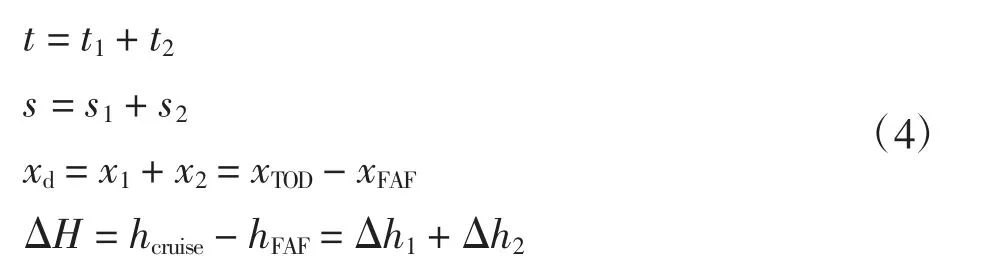
式中：t 为下降时间；s 为下降航段长度；xd为下降空域中下降的最大水平距离；ΔH 为下降高度；Δh1+Δh2为下降空域的最大下降高度。

CDA 路径的生成过程如下：

步骤1 确定飞机巡航高度hcruise，选取第1、第2下降航段加速度a1、a2，结合牛顿第二定律与CDA 受力平衡状态分析，求得飞机对应下降阶段的下降航迹角γα1、γα2；

步骤2确定初始下降速度vcruise，根据式（1）求得生成路径的下降时间t1、t2；

步骤3结合式（2）求得生成路径的下降航段长度s1、s2；

步骤4在步骤1 和步骤3 基础上，由式（3）可得下降的水平距离x1、x2。

1.2 动态CDA 路径实现与分析

用同心圆环结构表示某一高度层的下降空域，将下降空域在垂直方向上划分为N 层，同时按照水平安全间隔进行圆环半径划分，则下降空域高度h 和圆环半径r 分别表示为

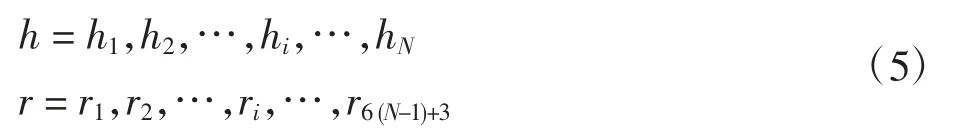
式中：h1为与标准地平面相差一个垂直间隔Δh 的高度；hN为最大下降高度（即最大巡航高度）；r1为FAF点与机场跑道的水平距离（r1=xFAF）。当i≥1 时，下降空域的垂直间隔Δh 和水平间隔Δr 的关系表示为

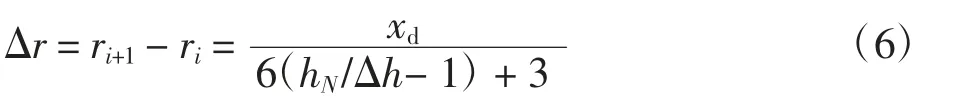
下降梯度ηα（百分比表示）与飞机下降航迹角γα的关系表示为

基于下降空域中划分的垂直、水平间隔，由飞机的下降梯度进行对应高度层的圆环选择，用多组圆环结构表示CDA 路径生成结构。设最大下降高度hN=14 000 m，与机场跑道的最大水平距离xd=248 n mile，FAF 点高度hFAF=500 m，与机场跑道的水平距离xFAF=5 n mile，机场跑道坐标为（0，0）。根据式（1）～式（7）和表1中CDA 路径生成模型数据，得到基于下降空域的CDA 路径生成模型，如图2所示。

表1 CDA 路径生成模型数据Tab.1 Data of CDA path generation model

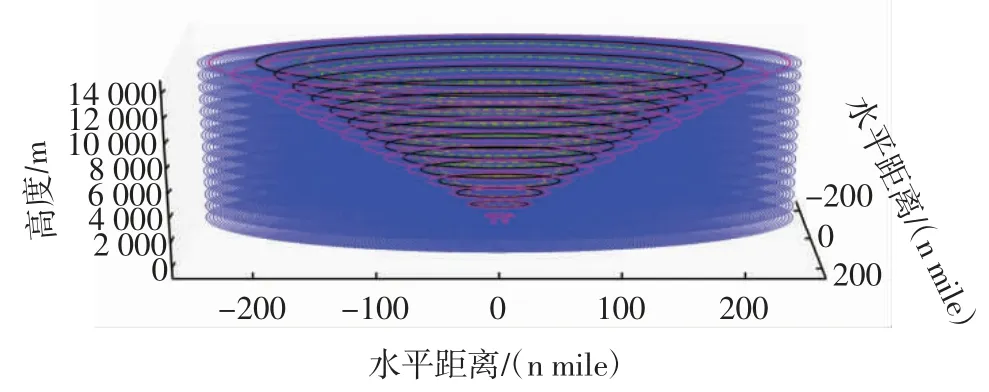
图2 基于下降空域的CDA 路径生成模型Fig.2 CDA path generation model based on descending airspace

图2中：所有圆环之间的区域为下降空域，垂直间隔Δh=1 000 m，水平间隔Δr=3 n mile，最底层中心星形图标位置为机场跑道位置（下同），底层圆环上的2 个方形图标位置为FAF 点位置（下同）；CDA 路径生成模型结构为具有相同线型、不同高度的圆环构成的中空倒立圆锥体，生成的CDA 路径点落在倒立圆锥体结构的圆环上。由表1数据得到的5 种CDA 路径生成结构都包含于下降空域结构内。

当飞机在同一下降航段选用不同加速度时，结合牛顿第二定律和CDA 的总受力平衡分析，求得的下降航迹角不同，下降梯度也会不同，则飞机在某一高度层时选取的圆环半径也将不同，即CDA 路径生成结构存在差异。CDA 路径对应的二维仿真图如图3所示。

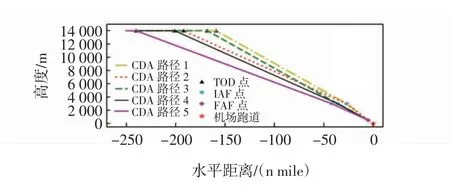
图3 CDA 路径二维图Fig.3 2D diagram of CDA path

图3中，CDA 路径1～5 分别与以上5 种CDA 路径生成模型相对应，5 种CDA 路径的对应参数如表2所示。

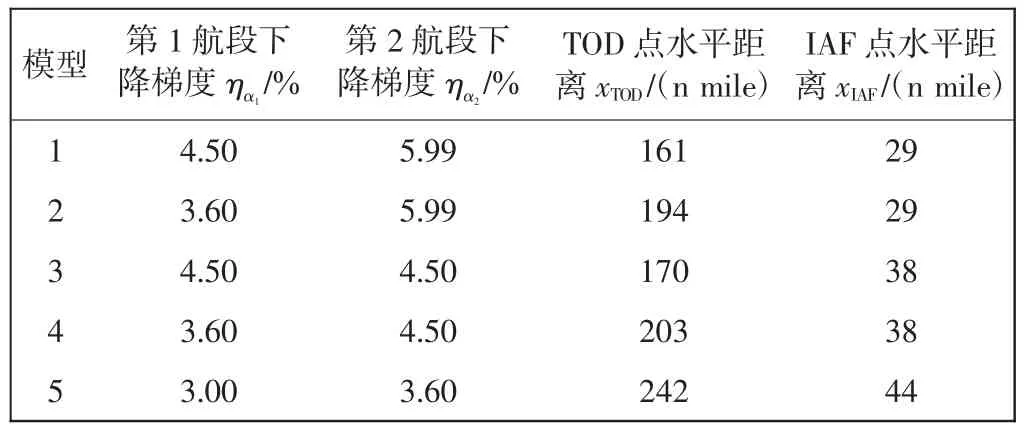
表2 不同CDA 路径的对应参数Tab.2 Comparison parameters of CDA path

结合表1和表2的数据，分析不同CDA 路径的参数特点。由牛顿第二定律可知，当选用的下降加速度越大，飞机总受力越大，对应飞机迎角越大，具有相同下降高度时，求得下降的水平距离越小，下降梯度越大。

2 CDA 路径筛选

2.1 基于空域范围差异的路径筛选

由牛顿第二定律研究CDA 过程中飞机受力的平衡状态方程，通过对最长下降航段和最短下降航段的分析得到基于下降进近受力平衡状态的终端区空域。在之前研究工作中已验证，相较于国际民航组织（ICAO）给出的标准下降空域范围，终端区下降空域范围缩小19.27%。根据标准下降空域和终端区下降空域的区域差异，构建基于某一高度层的路径范围筛选模型，实现CDA 的路径范围筛选。

在终端区下降空域中，第i 高度层上距机场跑道最近和最远下降路径点的水平坐标分别表示为

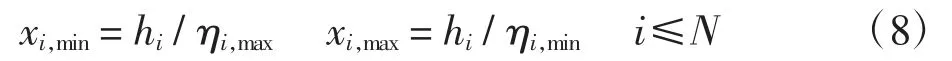
式中：hi为第i 层高度；ηi，max和ηi，min分别为终端区下降空域中第i 高度层的最大下降梯度和最小下降梯度。

由于标准下降空域范围大于终端区下降空域范围，则基于两者空域差异的路径范围筛选模型为

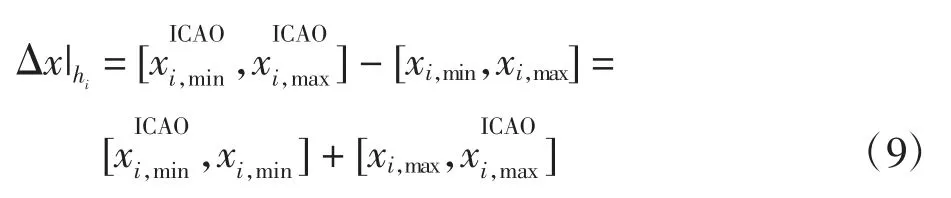
式中：Δx|hi为在hi高度上筛选模型的水平距离范围；和分别为标准下降空域中，在第i 高度层上距机场跑道最近和最远的TOD 位置。

已知标准下降空域和终端区下降空域的参数及多个特殊定位点的位置参数如表3所示。

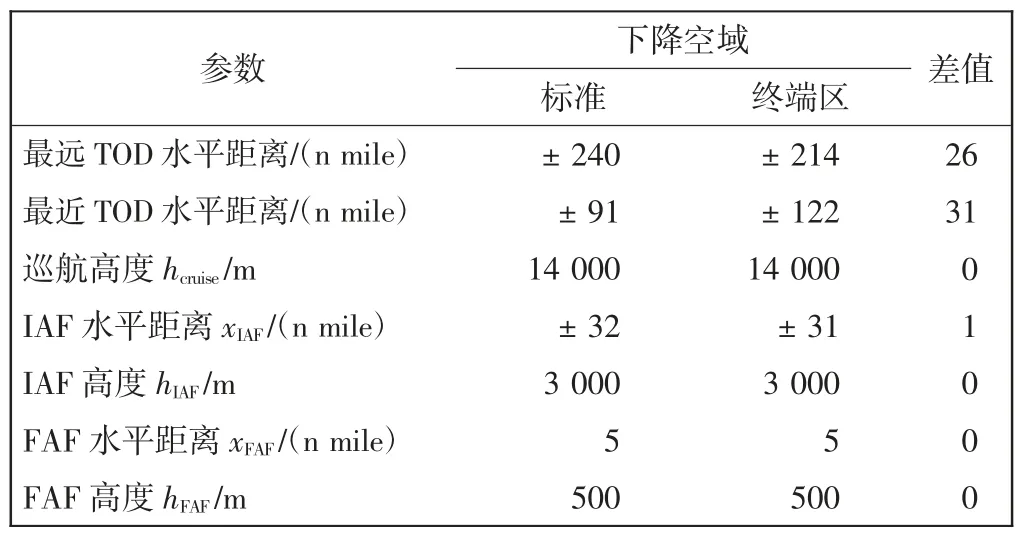
表3 标准下降空域和终端区下降空域参数Tab.3 Parameters of standard descent airspace and terminal area descent airspace

根据式（5）～式（7）和表3中的下降空域参数，在下降空域的水平、垂直间隔划分基础上完成2 种下降空域结构的三维空间呈现，如图4所示。

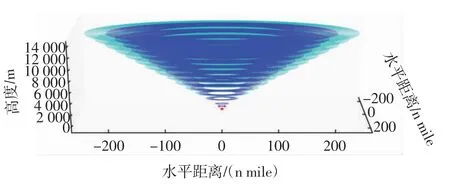
图4 标准下降空域和终端区下降空域结合图Fig.4 Combination diagram of standard descent airspace and terminal area descent airspace

图4中：圆环之间的区域为下降空域，下降空域结构实质是一个部分中空的倒立圆锥体；内部粗线条的倒立圆锥体结构为终端区下降空域结构，外部细线条的倒立圆锥体结构为标准下降空域结构。同一高度层中，标准下降空域结构的圆环数量大于等于终端区下降空域结构的圆环数量，说明了前者的下降空域范围比后者大。

默认CDA 路径在标准下降空域内生成，若CDA路径中不存在路径点落在筛选空域结构内，则该CDA路径为筛选路径。判断模拟CDA 路径的路径点位置是否落在筛选空域结构内来验证路径筛选模型的可行性。根据式（1）～式（4）、式（7）、表1中CDA 路径生成模型数据和表3中下降空域参数，结合下降空域划分的水平间隔和垂直间隔，完成筛选空域模型的路径验证，如图5所示。

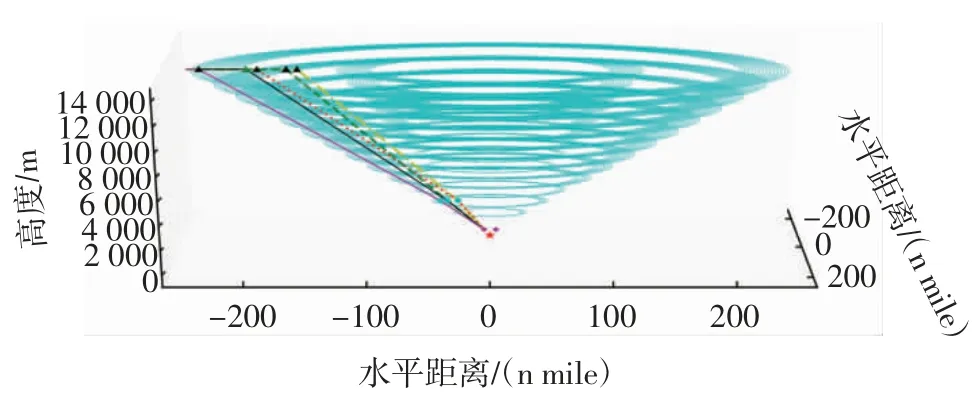
图5 筛选空域模型的路径验证图Fig.5 Path verification diagram of screening airspace model

图5中，圆环区域为筛选空域，由内到外的5 条CDA 路径对应图3中的路径1、3、2、4、5。由于路径5中的部分路径点落在筛选空域结构外，则只有路径1～4 为筛选CDA 路径。由随机模拟路径1～5 的路径筛选验证了路径筛选模型的可行性。

根据设定的下降空域数据求得CDA 路径筛选模型的范围，同时求得在垂直间隔为1 000 m 的划分基础上，即下降空域的高度h=1 000，2 000，…，14 000 m时，筛选模型区域与标准下降空域的比例为0%、0%、11.00%、12.10%、14.28%、11.11%、18.18%、19.23%、20.00%、20.58%、21.05%、23.80%、28.26%、32.00%。

2.2 基于路径点规划的路径筛选

为保证同一高度层中相邻飞机的下降安全，需要对下降空域中的圆环结构划分水平安全间隔，即完成每一高度层圆环的路径点规划。CDA 路径生成的实质是完成TOD 点高度层圆环到FAF 点高度层圆环上的路径点连接，通过筛选下降路径点的方式完成CDA 路径筛选。

具体高度层对应圆环上的路径点数目和相邻路径点之间圆心角的计算方程表示为

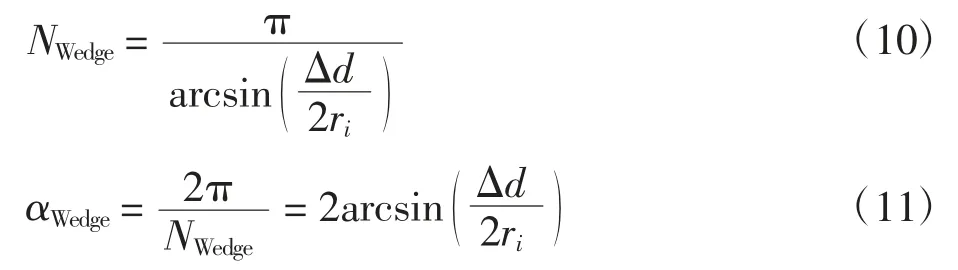
式中：Δd 为水平安全间隔；ri为第i 高度层对应的圆环半径。

在规划水平安全间隔的研究基础上，分析基于下降空域范围差异的路径筛选数目。设最大巡航高度为9 000 m，根据式（10）～式（11）和表3中标准下降空域与终端区下降空域参数，完成9 000 m 到500 m 对应高度层上的路径点规划，标准下降空域结构的路径点个数分别对应为1 869、1 502、1 101、791、488、268、156、72、11，终端区空域结构的路径点个数分别对应为1 195、941、719、524、362、229、126、54、11。从理论上计算：标准下降空域范围内，可生成的路径数目为1 869×1 502×1 101×791×488×268×156×72×11=3.95×1022条；终端区下降空域范围内，可生成的路径数目是1 195×941×719×524×362×229×126×54×11=2.63×1021条，则基于下降空域范围差异共筛选掉3.69×1022条CDA 路径。

选用表2中模型3 的下降数据，根据式（1）～式（6）和式（10）～式（11）完成CDA 的路径生成及不同高度层的路径点规划，得到基于路径点规划的CDA 路径结构（图6）及不同高度层对应的路径点参数。

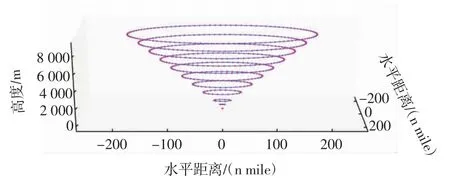
图6 基于CDA 路径生成模型的路径点规划图Fig.6 Path point planning diagram based on CDA path generation model

图6中，由不同高度层的圆环构成CDA 路径生成结构，最上层圆环的路径点为TOD 点，高度层越高，该高度层规划得到的CDA 路径点数目越多。在TOD 点高度层至FAF 点高度层上，完成相邻高度层上的路径点连接即生成CDA 路径。在CDA 路径生成结构中，从理论上计算，共有94×82×71×60×48×36×26×16×7×1=1.65×1014条CDA 路径。

3 CDA 路径优化

下降飞机在进行路径点转移时，需要满足规定的转弯角度要求。通过下降转弯角度限制、飞机受力平衡状态约束和最短航段距离规定，最终得到最优CDA路径。如果只研究从TOD 点到FAF 点的下降航段，只需考虑飞机在进场阶段和初始进近阶段的限制要求。文献[14]规定飞机在进场阶段和初始进近阶段的转弯角度应当小于等于110°。

文献[15]提出2 条航段之间的转弯角度可由相邻航向角之差表示。如果是相对于机场地面导航台，这个角就是飞机前进的方向和飞机的实际位置到机场地面导航台之间的连线夹角，转弯角度的计算示意如图7所示。

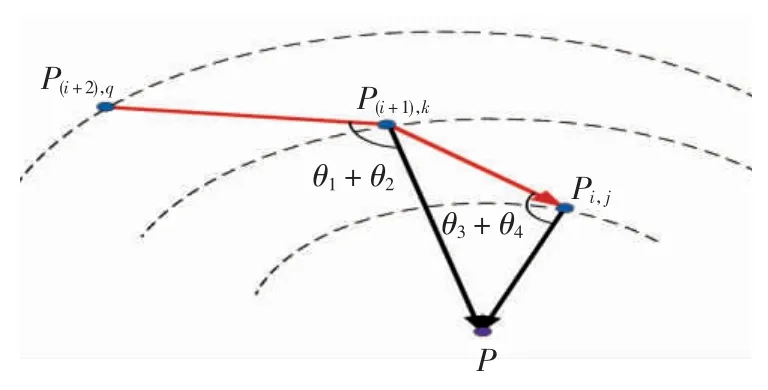
图7 转弯角度计算示意图Fig.7 Illustration of turning angle calculation

图7中：P(i+2)，q、P(i+1)，k、Pi，j分别为相邻高度层圆环上的路径点位置；P 为机场地面导航台位置。根据余弦定理的推导定理及航向角定义得知，θ1+θ2为飞机从P(i+2)，q位置飞向P(i+1)，k位置的航向角，θ3+θ4为飞机从P(i+1)，k位置飞向Pi，j位置的航向角。在笛卡尔坐标系中，航向角的计算方程表示为

CDA 下降转弯角度限制方程表示为

在CDA 路径点规划基础上，根据式（12）～式（14），进行下降转弯角度限制完成CDA 路径优化。设置下降转弯角度分别为50°和30°，得到下降转弯角度限制为50°和30°时的CDA 路径，如图8所示，同时计算可得2 种下降转弯角度限制条件下的CDA 路径数目。

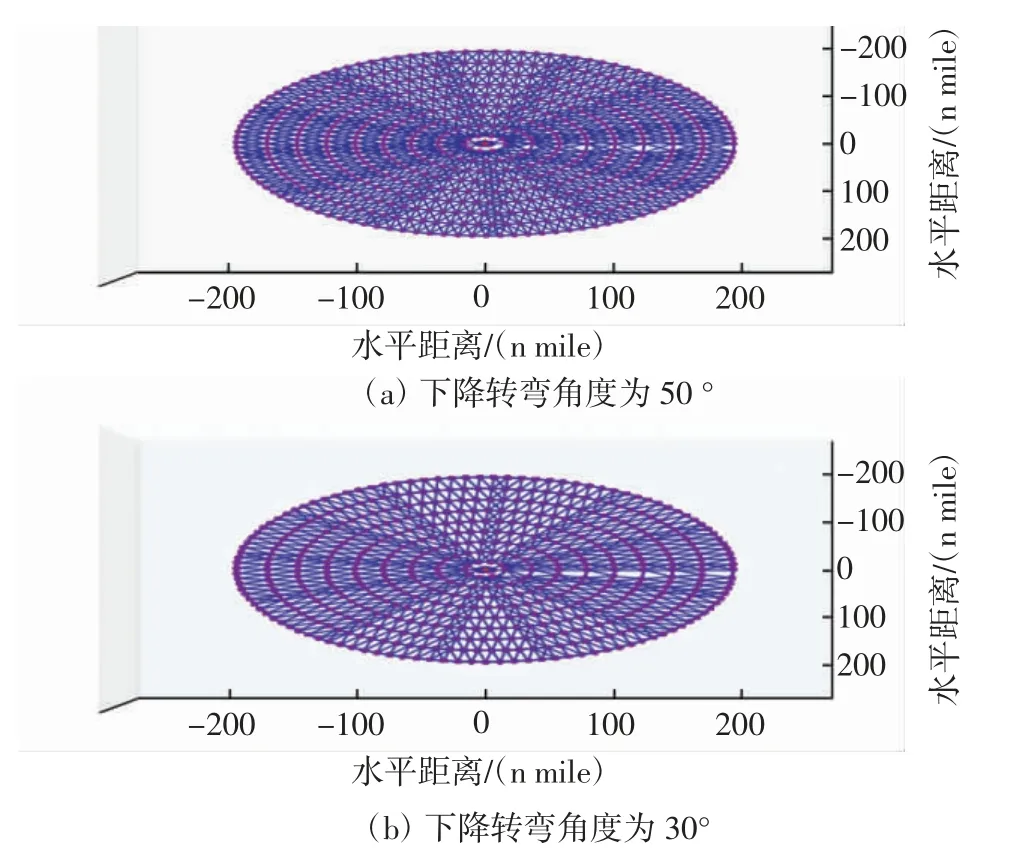
图8 不同下降转弯角度限制的CDA 路径点连接图Fig.8 CDA path point connection diagram restricted by different descent turning angles

图8中，最外层圆环上的点位置为TOD 点，圆环之间线段为由不同高度层路径点进行连接得到的CDA路径。对比图8（a）和图8（b）：下降转弯角度限制为30°时的路径数目更少，则下降转弯角度限制越小，生成的路径数目越少。下降转弯角度限制为50°时，生成的路径有1 478 条，当确定TOD 点后，路径减少为162条；下降转弯角度限制为30°时，生成的路径共有786 条，当确定TOD 点后，路径减少为32 条。

飞机达到受力平衡状态时的迎角区间为[0°，5°]，根据式（7）求得对应下降梯度范围为[0，8.99%]。根据该下降梯度范围限制，结合垂直安全间隔1 000 m和水平安全间隔3 n mile，下降转弯角度限制为30°时，确定TOD 点对应的路径点坐标为（-2.85，-175.98，9 000），得到9 条CDA 优化路径如图9所示。

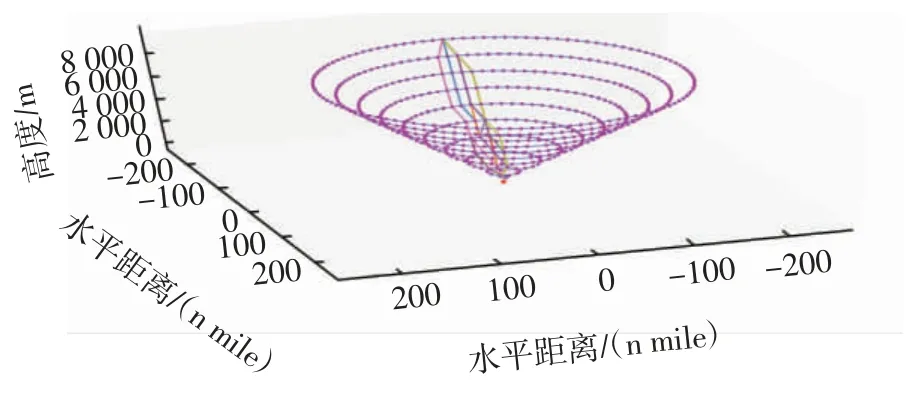
图9 优化CDA 路径图Fig.9 Diagram of optimal CDA path

经由相邻高度层路径点之间的距离求和，得到CDA 优化路径的航段距离，即

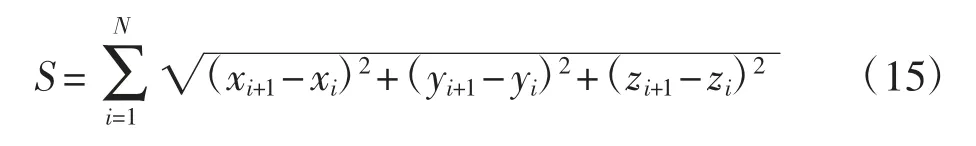
式中（xi，yi，zi），（xi+1，yi+1，zi+1）分别为第i 高度层对应路径点和第i+1 高度层对应路径点的坐标。根据式（15）求取CDA 优化路径的下降航段距离，如表4所示。

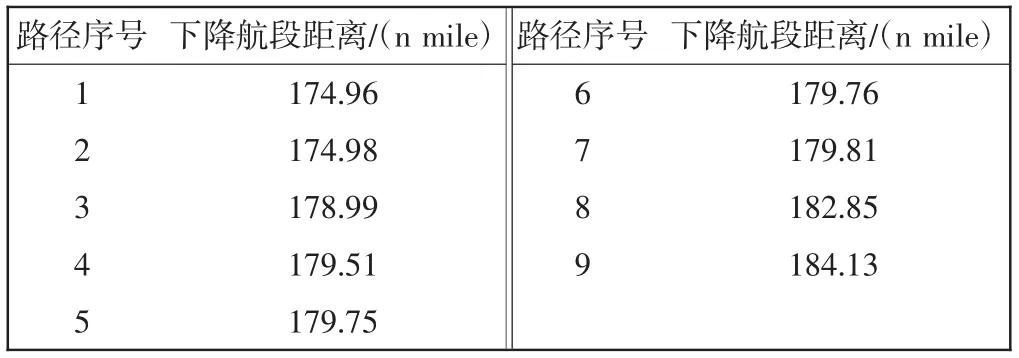
表4 CDA 优化路径的下降航段距离Tab.4 Descent segment distance data of the CDA optimization path

从表4可看出，路径1、2 的下降航段距离相近且最短，选定路径1、2 为最优CDA 路径。最优CDA 路径如图10所示，其中，不同线型的线段为最优CDA 路径，确定TOD 点位置的2 条最优CDA 路径在高度4 000～9 000 m 范围内选择不同路径点连接，在进近阶段的下降路径点相同。

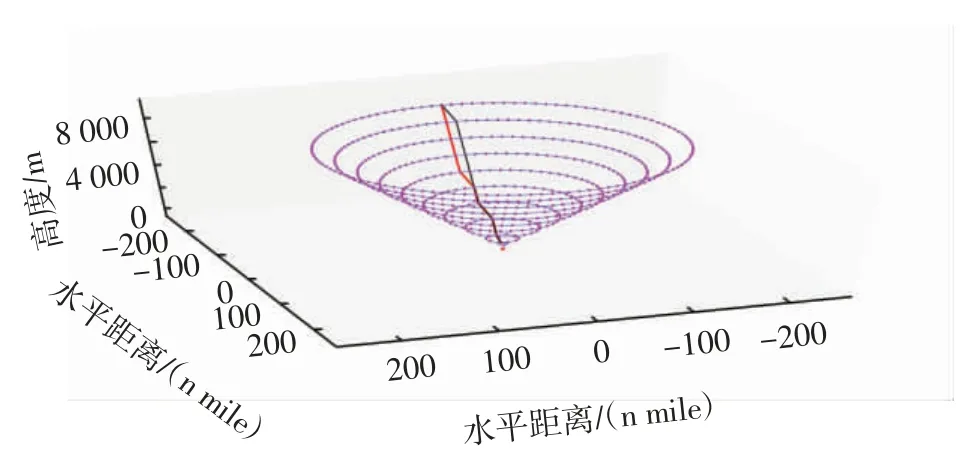
图10 最优CDA 路径图Fig.10 Diagram of the best optimized CDA path

4 结语

基于水平安全间隔和垂直安全间隔构建动态CDA 路径生成模型，CDA 路径生成模型呈现为圆环组成的中空倒立圆锥体。基于2 种下降空域的区域差异建立了路径范围筛选模型，随机模拟CDA 路径的验证结果证明了该模型的可行性。通过下降路径点规划进行路径筛选，最终得到1.65×1014条CDA 路径。当下降转弯角度限制为30°，在满足飞机达到受力平衡状态条件下进行最优航段距离选择，得到确定TOD 点的2 条最优CDA 路径。不同TOD 点对应多条最优CDA路径，能够实现多架飞机在同一终端区空域内的安全下降，可有效提高民航运输效益。