Gerhards模型在针叶木材长期寿命预测中的适用性分析*

王忠铖 杨 娜

( 北京交通大学土木建筑工程学院 结构风工程与城市风环境北京市重点实验室 北京 100044)

木材的长期承载能力远低于暂时承载能力，在长期荷载作用下，木材会发生纤维等速蠕滑,累积后产生较大变形，强度降低，且施加荷载越大，木材从受荷开始至破坏的时间越短(龙卫国， 2005)。20世纪50—80年代，国外学者对木材长期强度进行了大量试验研究(Brokawetal.， 1952； Youngsetal.， 1963； James， 1968； Mcnatt， 1975； Strickleretal.， 1976)，基于金属疲劳破坏的Miners准则(Schijve， 2014)提出一种线性累积损伤理论，用以解释木材长期受荷作用下强度降低的现象(Gerhards， 1979)，即Gerhards模型：

(1)

式中：σ(t)为外应力；fs为木材静力强度；α为损伤累积量，其变化范围为[0，1]，α=0表示木材无损伤，α=1表示木材失效；A、B为待拟合参数。

Gerhards模型形式简单，以往众多木材长期受荷性能研究均以该模型为基础(Fridleyetal.， 1989； 1990； 1991； Kuilen， 2007； 李瑜， 2008； Srensenetal.， 2005； 瞿伟廉等， 2008； Qinetal.， 2017； Wangetal.， 2019)； 然而，所有基于Gerhards模型的木材寿命预测研究，均普遍存在模型参数选取问题，Gerhards模型是一个指数形式的函数，参数的微小差异会导致寿命预测结果的巨大差别(Wangetal.， 2019)。

鉴于此，本研究分析木材长期寿命预测中常用Gerhards模型的适用性，探讨参数选取对不同加载工况下模型预测结果的影响，同时针对木材寿命预测中预测值大于真实值的问题，提出一种基于Gerhards模型的区间预测模型分析方法，以期为进一步提高木材长期寿命预测精度提供理论依据。

1 Gerhards模型的适用性分析

1.1 Gerhards模型与Gerhards试验对比

Gerhards模型的数学表达式最早由Gerhards(1979)提出，随后其开展了包含6种工况的北美花旗松(Pseudotsugamenziesii)四点弯曲线性加载和恒定加载试验(Gerhards试验)(Gerhardsetal.， 1987)，木材试样横截面尺寸约50 mm×100 mm(宽×高)，跨度约2 100 mm，试验期间环境温度24 ℃，相对湿度55%，各试验加载工况见表1。

表1 Gerhards试验的加载工况①Tab.1 Loading conditions of Gerhards’s experiment

Gerhards试验获得了不同线性加载速率和恒定加载量级下的木材破坏时间，对不同加载工况进行组合，共拟合得到8组Gerhards模型参数A和B，见表2。

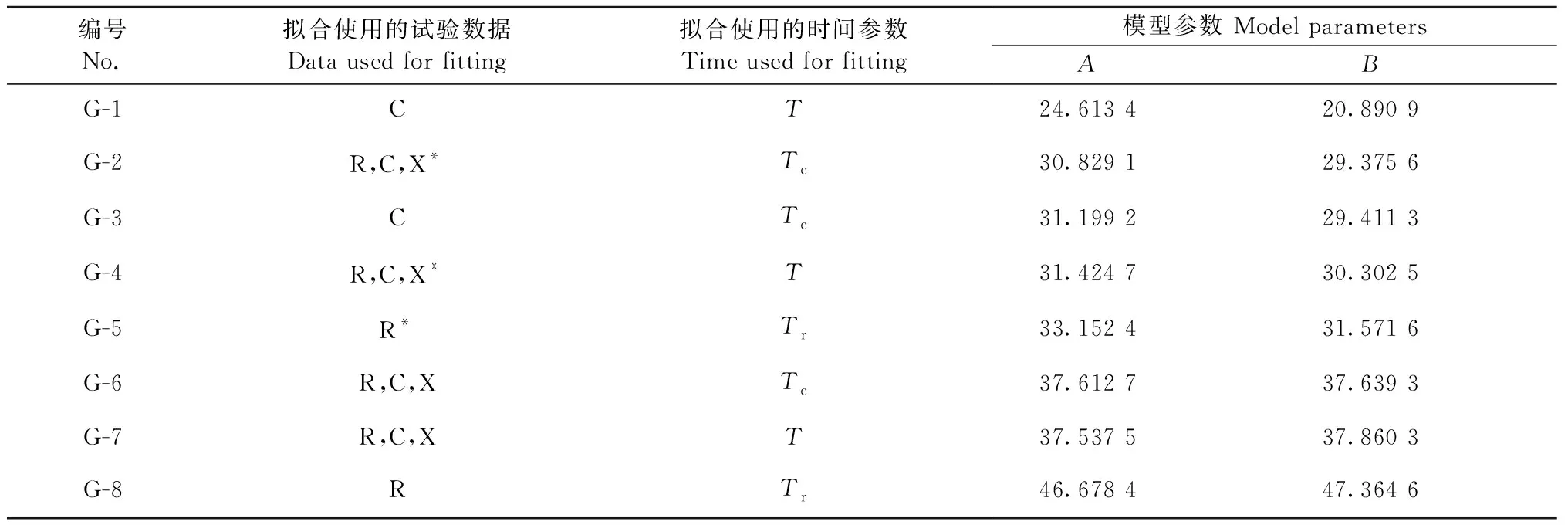
表2 Gerhards模型的8组模型参数①Tab.2 8 sets of model parameters of Gerhards model

Gerhards模型参数拟合自Gerhards试验数据，由于各模型参数源于不同加载工况组合，因此本研究首先分析Gerhards模型在预测Gerhards试验6种工况时的适用性。

对式(1)积分，可推导出木材破坏时间FD(failure duration)(min)与线性加载速度k(N·min-1)或恒定应力水平SL(stress level)的关系：

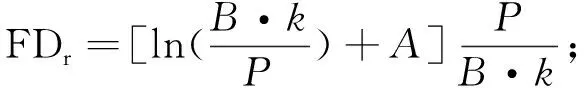
(2)

FDc=exp(A-B·SL)。

(3)

式中：P为单位换算系数，P=3 168.89； FDr、FDc分别为线性加载和恒定加载木材破坏时间。

将8组Gerhards模型参数代入式(2)和(3)，计算出各模型对各工况试样破坏时间的预测值见表3，其中各工况下试样破坏时间的中位数参考Gerhards等(1987)。

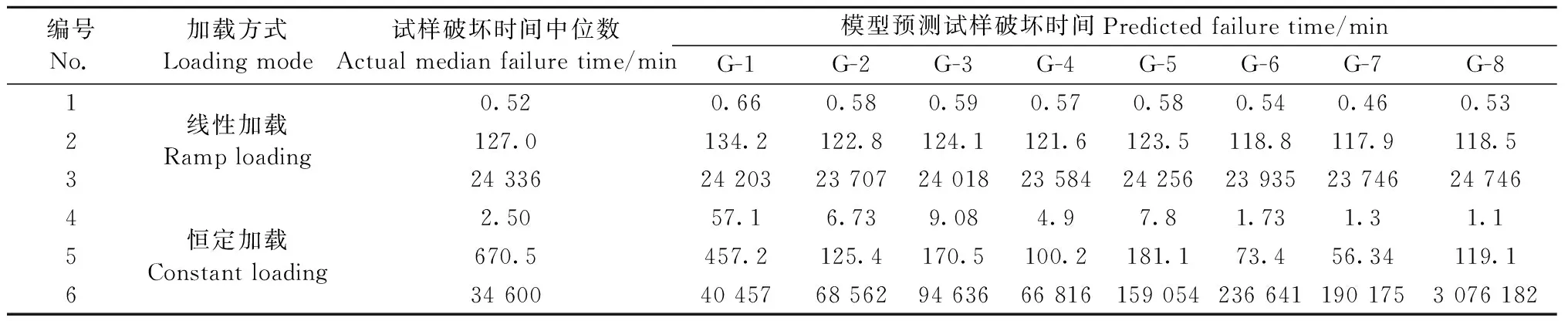
表3 Gerhards试验中试样破坏时间中位数与各模型预测值对比Tab.3 Comparison between actual median failure time of Gerhards’s experiment and predicted failure time

由表3可知，8组Gerhards模型在预测线性加载的3种工况时，各模型预测值接近，且与试验值偏差较小。对于工况1，模型预测误差的最小值和最大值分别为1.92%(G-8)和27.92%(G-1)； 对于工况2，模型预测误差的最小值和最大值分别为2.28%(G-3)和7.17%(G-7)； 对于工况3，模型预测误差的最小值和最大值分别为0.33%(G-5)和3.09%(G-4)。8组Gerhards模型在预测恒定加载的3种工况时，各模型预测精度普遍低于线性加载工况。对于工况4，模型预测误差的最小值和最大值分别为30.80%(G-6)和2 184.00%(G-1)； 对于工况5，模型预测误差的最小值和最大值分别为31.81%(G-1)和91.60%(G-7)； 对于工况6，模型预测误差的最小值和最大值分别为16.93%(G-1)和8 790.70%(G-8)。由此可见，与线性加载工况相比，恒定加载工况下各模型预测值间差别较大，且个别模型预测值与试验值差异极大。这是因为Gerhards模型在预测线性加载工况时，FD与k为乘积关系(式2)，而在预测恒定荷载工况时，FD与SL为指数关系(式3)，参数的微小差异会导致预测结果的巨大差别。实际服役过程中，木结构主要承受恒定荷载，因此基于Gerhards模型预测木材寿命前，必须明确各模型的适用范围，否则会使木材寿命预测值远大于真实值，预测结果偏于危险。

1.2 Gerhards模型与恒定荷载试验对比

木结构构件所受SL普遍较小，构件寿命往往相对较长。本研究选取同样为长期恒定荷载的2类针叶材试验，即Wood和Hoffmeyer试验数据进行对比(Wood， 1951； Hoffmeyeretal.， 2007)，以分析Gerhards模型在木材长期寿命预测中的适用性。

Wood试验为抗弯试验，用材为北美花旗松，试样横截面尺寸约50 mm×50 mm(宽×高)，含水率为6%和12%，SL介于60%～95%之间； Hoffmeyer试验同样为抗弯试样，用材为欧洲云杉(Piceaabies)，试样尺寸约1 800 mm×44 mm×95 mm(长×宽×高)，含水率为11%和20%，SL介于55%～105%之间。2类木材的基本物理力学性质见表4(龙卫国， 2005)。

表4 长期受荷试验用2类针叶材的物理力学性质参考值Tab.4 Reference value of the physical and mechanical properties of the softwood used in the long-term load test

将8组Gerhards模型与Wood和Hoffmeyer试验数据在“SL-lgFD”坐标系下对比，以反映预测曲线与试验数据之间的关系(Wangetal.， 2019)，见图1。

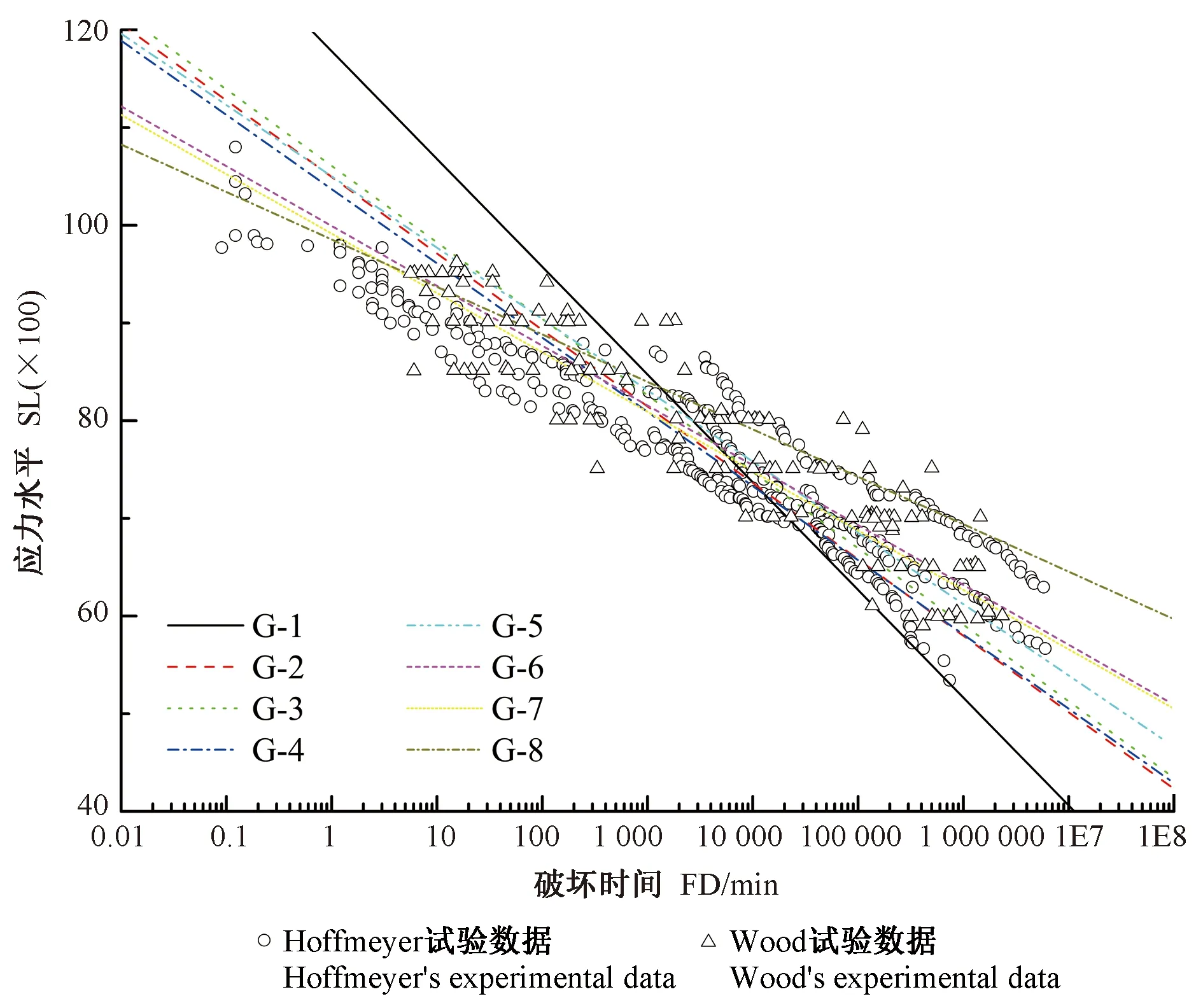
图1 Gerhards模型与恒定载荷试验数据对比Fig. 1 Comparison between Gerhards model and constant experimental data

由图1可知，除G-1模型外，其余模型均能较好穿过试验数据点，模型对试验值预测较好。对于G-1模型，当SL大于80%时，模型预测的破坏时间普遍大于试验值； 当SL小于80%时，模型预测的破坏时间普遍小于试验值。

为了量化各模型预测效果优劣，计算各模型对SL预测值与试验值的均方误差(mean square error，MSE)：

(4)

式中：xi为预测值；μ为试验值；n为试验数据总样本量。

各模型预测效果的均方误差见表5，其中Wood试验数据与模型预测值之间的均方误差参考Wang等(2019)。

表5 各模型对SL预测值与试验值的均方误差Tab.5 MSEs between predicted and experimental SLs

由表5可知，对于Wood长期恒定载荷试验，G-5—G-8模型预测效果较好，G-2—G-4模型预测效果较差，G-1模型预测效果最差； 对于Hoffmeyer长期恒定载荷试验，G-6—G-7模型预测效果较好，G-2—G-5和G-8模型预测效果较差，G-1模型预测效果最差。出现这种差异的原因在于各模型加载工况与被预测对象加载工况的相似程度。以Wood试验为例，表6对比了Gerhards与Wood试验中相似SL下试样破坏时间。

表6 Gerhards与Wood试验中相似SL下试样破坏时间对比Tab.6 Comparison of median failure time under similar SL between Gerhards’s and Wood’s experiments

由表6可知，对于Gerhards试验工况6，试样破坏时间中位数与Wood试验中相似SL下试样破坏时间中位数差异极大； 而对于工况4、5，差异则相对较小。由此可见，在预测Wood试验数据时，Gerhards模型中工况6数据占比越大，模型预测精度越低，因此G-1—G-4模型的预测效果劣于G-5—G-8模型。同理可分析Gerhards模型对Hoffmeyer试验数据预测效果优劣的原因。

综上所述，当木材试样为承受SL介于60%～95%的北美花旗松时，建议采用G-6模型进行寿命预测； 当木材试样为承受SL介于55%～105%的欧洲云杉时，建议采用G-7模型进行寿命预测； 当木材试样承受SL小于50%时，建议采用G-1模型进行寿命预测。有研究曾对比8类木材【花旗松及其胶合木、台湾柏(Juniperusformosana)、日本柳杉(Cryptomeriajaponica)、北美云杉(Piceasitchensis)、桦木(Betulaspp.)、枫木(Acerspp.)、圆果桉(Eucalyptuspilularis)，前5类属于针叶材，后3类属于阔叶材】试样持续受荷试验结果发现，尽管树种、截面尺寸和含水率不同，但木材寿命与SL有很好的一致性(Pearson， 1972； 樊承谋等， 2008)。因此，当被预测木材树种、尺寸和含水率与本研究分析使用的北美花旗松和欧洲云杉木试样不同时，Gerhards模型预测值仍可作为参考。

2 基于Gerhards模型的SLC区间预测模型分析方法

由上述分析可知，当预测模型所用数据的加载工况与被预测对象的受荷工况相似时，模型具有较好预测效果，本研究称这类基于相似工况试验数据拟合的模型为SLC(similar loading condition)模型。由图1可知，虽然Gerhards模型曲线穿过Wood和Hoffmeyer试验数据点围成的区域，但仍有相当一部分数据位于曲线左下方，即模型预测的试样破坏时间极有可能大于试样实际破坏时间，这对于木材寿命预测是偏危险的。鉴于此，本研究提出一种基于Gerhards模型的SLC区间预测模型分析方法，以改进木材长期寿命预测精度。

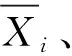
(5)

上述统计量汇总于表7。

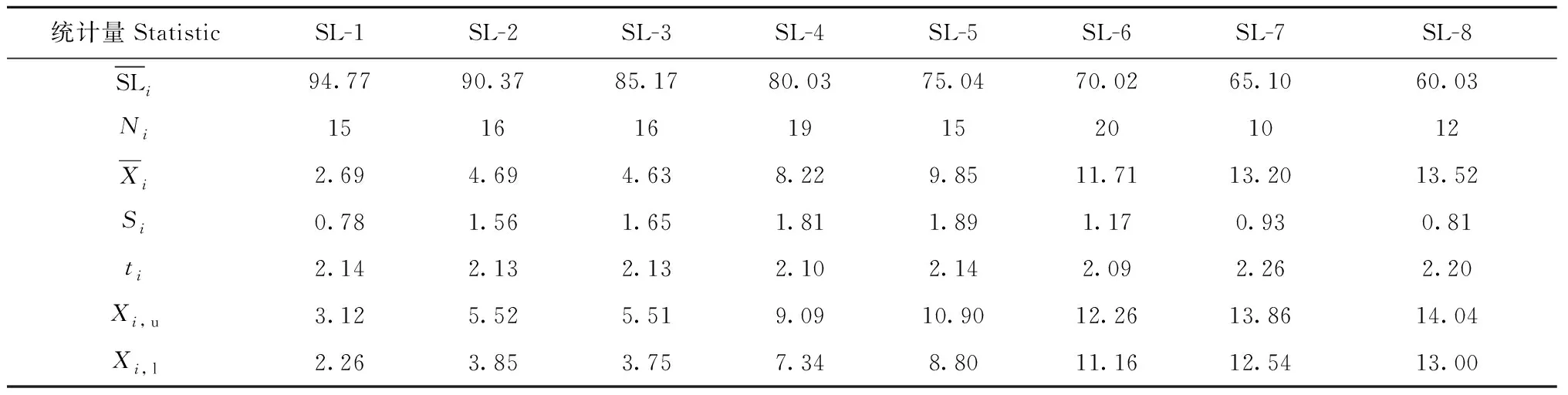
表7 Wood恒定载荷试验数据的统计量Tab.7 Statistics of Wood’s experimental data

由式(3)可知，木材受恒定载荷时SL与FD存在以下关系：

SL=m-n·lnFD。

(6)

式中：m和n为待拟合参数。

由图2可知，蓝色虚线包络区域为采用上、下限模型得到的寿命预测区间，因经过一次由lnFD到FD的计算，区间过度向均值模型曲线靠拢，导致仍有大量试验点落在区间外。

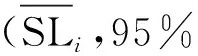
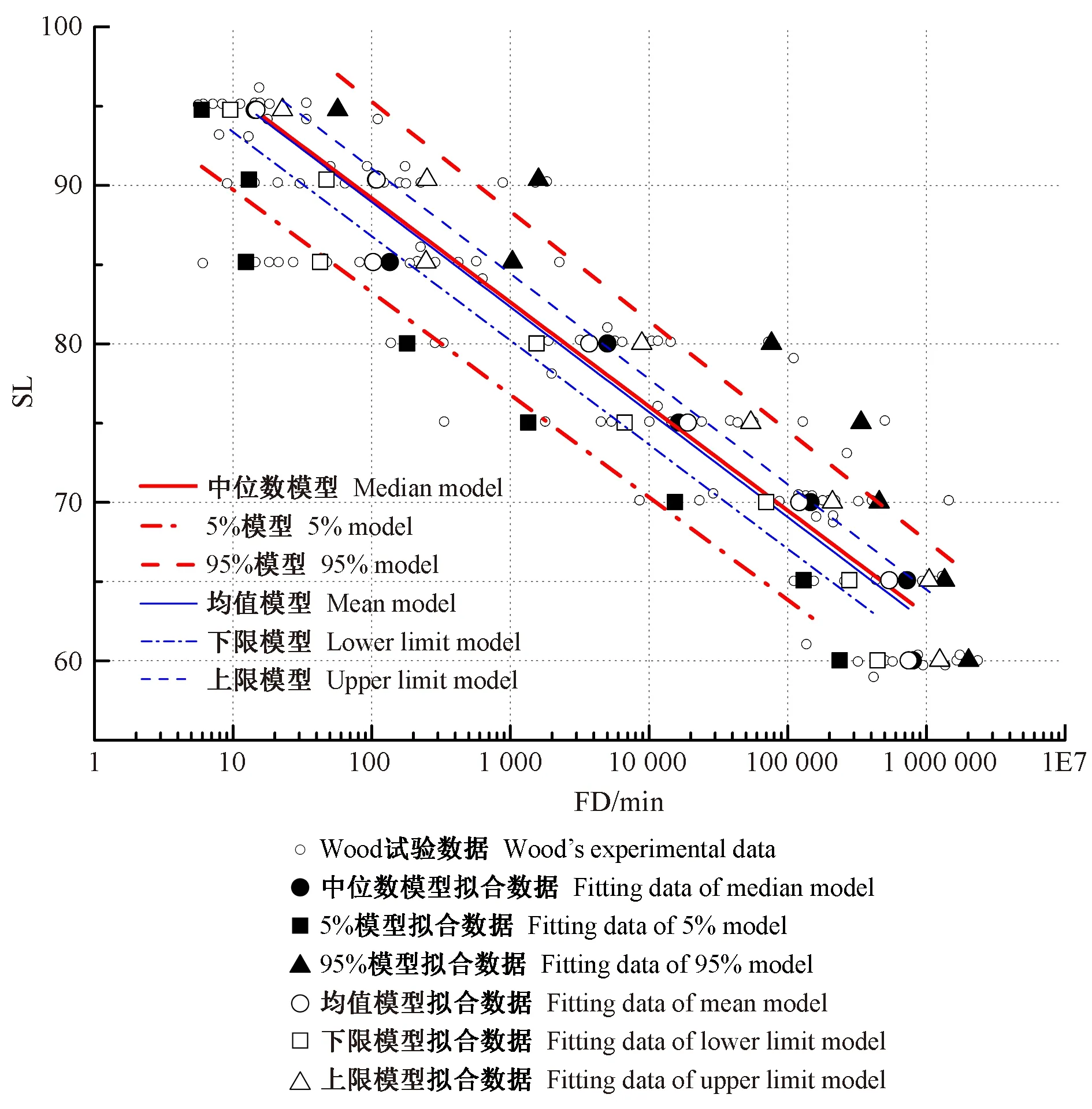
图2 基于Wood试验数据的区间预测模型Fig. 2 Interval prediction model based on Wood’s experimental data

以上2类区间模型表达式中的m、n统计于表8。

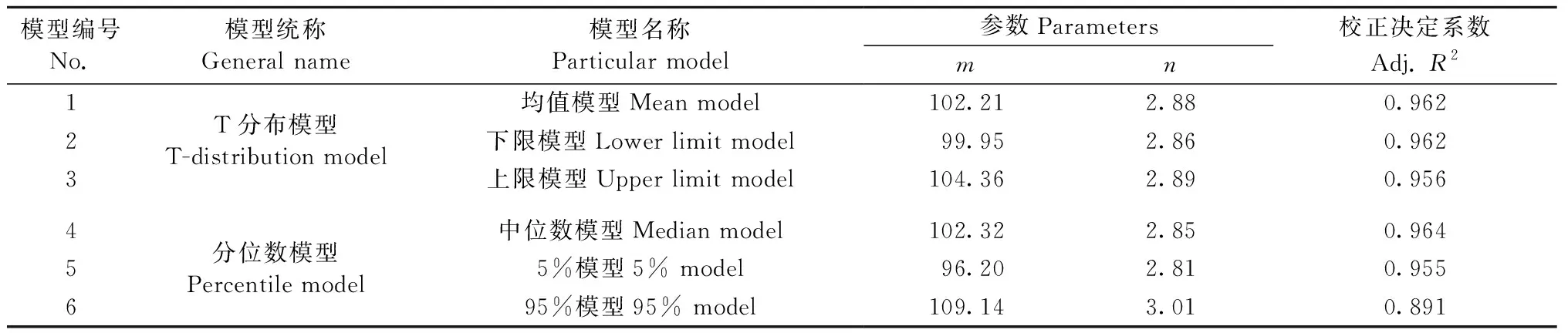
表8 基于Wood试验数据的2类区间预测模型参数对比Tab.8 Comparison of parameters of two interval prediction model based on Wood’s experimental data

由图2和表8可知，均值模型与中位数模型十分接近，说明T分布模型与分位数模型相对于试验数据点的位置近乎同心，只是包络宽度不同，使用分位数模型可使绝大部分试验数据点落在区间模型内，从而避免寿命预测值大于真实值。因此，对于相似受荷试验数据的情况，在木材寿命预测时建议参考本研究提出的基于Gerhards模型的SLC区间预测模型分析方法，以提高木材寿命预测精度。

3 结论

1) 不同工况组合拟合得到的模型具有不同适用范围，不加区分地应用模型会使木材寿命预测精度大幅降低。以对Gerhards试验数据的预测结果为例，各Gerhards模型对线性加载工况下木材寿命预测值较为接近，预测结果较为精确，预测误差介于0.33%～27.92%之间； 各Gerhards模型对恒定荷载工况下木材寿命预测值差异较大，预测精度较差，预测误差介于16.93%～8 790.70%之间。

2) G-6模型适用于SL介于60%～95%的北美花旗松寿命预测，G-7模型适用于SL介于55%～105%的欧洲云杉寿命预测，SL小于50%建议采用G-1模型进行寿命预测。当被预测木材树种、尺寸和含水率与本研究分析使用试样不同时，Gerhards模型预测值仍可作为参考。

3) 当预测模型所用数据加载工况与被预测对象受荷工况相似时，模型具有较好预测效果。SLC区间预测模型可有效避免模型预测寿命大于木材实际寿命的问题，基于试验数据分位数拟合的预测模型较基于T分布假设拟合的预测模型涵盖更多试验数据点。

需要注意的是，木材是一种生物建材，与其他常用建筑材料相比，木材力学性能的离散性相对较大，因此，木材力学性能本身差异同样可能导致Gerhards模型预测值与试验值之间的差异。此外，本研究采用的试验数据均为隔离环境因素影响的北美花旗松和欧洲云杉实验室数据，模型预测值较真实环境中的木材寿命可能存在一定偏差，但对受环境影响较小的室内木结构木材寿命预测仍具有一定参考价值。更进一步地精确预测木材寿命，可在本研究分析Gerhards模型的基础上考虑各种环境因素的影响，或直接采用SLC区间模型分析方法对包含环境因素影响的试验数据进行拟合，进而得到更为精确预测真实环境中木材寿命的模型。