基于调节阀流量特性曲线的前馈控制系统设计①
陈 晨 尚群立 陈艳宇
(浙江工业大学信息工程学院 杭州310023)
0 引言
液位调节系统是一个典型的过程控制系统,广泛应用于各领域。其中对液位的控制是至关重要的。深入研究液位控制策略以及液位波动问题,能够为工业生产以及过程控制提供重要的理论指导。
在液位控制系统中,已知干扰大小与各环节的传递函数,通常使用前馈加反馈的控制策略能有效消除干扰对于液位的影响[1-2]。针对单输入单输出线性系统,文献[3]提出用常规极点配置控制器来保证闭环系统的稳定性。文献[4]用高阶干扰观测器来补偿外部干扰对于闭环系统的影响。为了克服噪声与干扰,文献[5-8]使用上一时刻的干扰来估计当前时刻的干扰,并使用Smith 预估计补偿与基于无轨迹卡尔曼滤波和快速预测控制相结合的控制器设计方法来抗干扰。液位控制系统不仅仅可以使用传统的比例积分微分控制(proportion integration differentiation,PID),还可以使用PID 中的3 个参数作为3 个维度,采用目标函数自适应的惯性权重系数调整策略,对PID 控制进行优化[9];同样可以利用内模控制去控制液位,使调参简便,更有效地改善系统性能[10]。针对延时过程,文献[11]通过预测函数控制(predictive functional control,PFC)优化PI 控制器,使其性能优于PI 控制器。针对非线性行为,文献[12]利用模型去捕获过程控制站的非线性行为,并通过调整控制器来适应系统动态变化。在液位控制系统中至关重要的控制元件是调节阀,文献[13,14]利用流体动力学(computational fluid dynamics,CFD)仿真软件去模拟阀芯形状对于流量特性曲线的影响。为了稳定调节阀出口流量,文献[15]利用调节阀的开度以补偿压降。
上述研究从零极点配置、预测控制、内模控制、先进PID 控制等角度去分析前馈控制策略或者消除干扰的影响。调节阀的流量特性曲线是固有特征,反映在压差固定的情况下,阀位与流量的关系。但是由于调节阀安装在管路工艺系统中,与管路系统中其他节流部件共同参与阻力分配,使阀的固有流量特性曲线发生畸变,故调节阀的流量特性选型要结合整个工艺流程与控制目标。文献[16]使用海底静力触探所采集的锥尖阻力和侧壁摩檫力作为前馈控制的输入量。而本文以实验研究为主,在大量实验中发现与总结规律,利用实际工况参数并从调节阀工作流量特性曲线的角度去解释和研究如何确定前馈补偿系数。阀位与流量间存在非线性,使所求前馈补偿器不具有通用性。针对调节阀阀位与流量呈非线性的现象,本文提出一种阀位补偿算法,使阀位与流量呈线性关系,前馈补偿系数更具有通用性。
1 前馈补偿系数的设计
1.1 经典前馈-反馈复合控制
经典反馈系统的本质是“基于偏差来消除偏差”,是一种“不及时”的控制,无论扰动发生在哪里,总要等被控量发生偏差后,调节器才开始调节,调节器的动作总要落后于扰动。前馈控制的特点是“基于扰动来消除扰动对被控量的影响”,又称为“扰动补偿”。扰动发生后,前馈控制“及时”动作,只适合于可测(扰动量可以通过测量变送器,在线地将其转换为前馈补偿器所能接受的信号)不可控的扰动,控制规律取决于被控对象的特性。前馈控制是使前馈环节与闭环系统的传递函数之积为1[17-18],从而实现输出完全复现输入。前馈-反馈复合控制方框图如图1 所示。

图1 前馈-反馈复合控制方框图
在F(s) 作用下,系统输出为

前馈补偿器的设计为
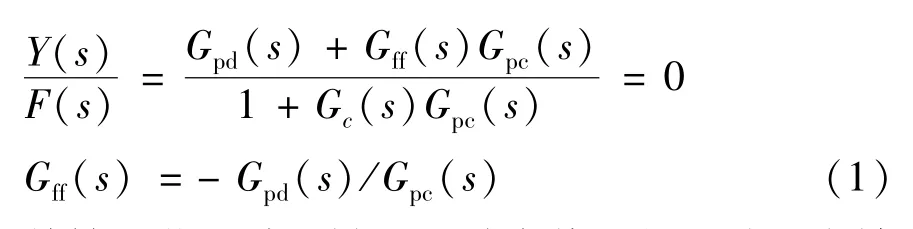
前馈调节是减少被调量动态偏差的一种最有效的调节策略,但是在工业生产中前馈调节系统实际上是无法采用的,主要原因如下。
(1) 实际工业生产中,使被调量变化的原因(扰动)较多,对每一种扰动都需要一个独立的前馈调节,导致调节系统变得复杂。
(2) 对于某一个可测量的扰动,由于式(1)传递函数Gpd(s)、Gpc(s) 求解困难,并且求解后精度不高,所要求的理想前馈控制器在物理上较难实现。在工业生产中,大量使用调节阀,调节阀虽能近似等效成一阶加惯性环节,但调节阀中存在定位器,定位器内同样存在闭环控制系统,并且具有特殊的控制算法以确保阀位能快速并准确达到设定值,故想得到精确的调节阀传递函数模型基本不可能。
(3) 传递函数Gpd(s) 和Gpc(s) 都存在较强的非线性,Gpd(s) 和Gpc(s) 随着工况的不同而变化,即不同工况、不同干扰下的前馈补偿器存在差异,不具有通用性。
1.2 基于流量特性曲线设计前馈补偿系数
常见的单闭环液位控制系统如图2 所示。调节阀用来控制管路中流量的大小,调节阀调节流量的能力是根据其流量特性曲线所决定的。阀的流量特性曲线定义为被控介质流过阀门的相对流量与阀门的相对开度间的关系。常见的流量特性曲线如图3所示。三条流量特性曲线能提供相同的最大流量。但选择不同的流量特性曲线会使控制效果产生差异。

图2 液位控制系统

图3 常见的流量特性曲线[19]
由1.1 节可知,传统的前馈-反馈控制策略应用于所有工况较为困难。针对该问题,本文提出一种根据实际工况参数与调节阀工作流量特性曲线来确定前馈补偿系数的方法。确定前馈静态补偿系数的原理如下,已知液位控制系统的开环实验数据,如阀位、流量、液位、阀前阀后压力等,根据各个物理量间的函数关系,便可近似获得已知所有工况下系统中的工艺参数。例如在某个液位,通过工艺参数间的函数关系,便能计算出液位稳定时的阀位pv和管路中的流量Q。加入扰动流量R后,为了保持液位稳定,管路中所需要提供的流量应减小至Q -R,并通过流量与阀位的函数关系求取此时的阀位pv1。若没有前馈补偿器,那么液位反馈控制系统会调节阀位,使阀位从pv调节至pv1。调节需要一定的时间,故在调节过程中液位会发生波动。加入前馈补偿器,在扰动加入后,使阀位直接调整为pv1,让液位系统保持稳定。
前馈系数确定步骤如下。
(1)根据液位控制系统的开环实验数据获取液位信号h与管路中的流量信号Q,获得两者间函数关系f(x):Q=f(h)。
(2)根据开环数据获取管路中流量信号Q与阀位信号pv,获得两者间函数关系g(x):pv=g(Q)。
(3)当设定液位为h1 时,根据函数f(x),可得该液位h1 下,管路中的流量信号Q1。
(4)已知流量信号Q1,根据函数g(x),可得该流量下的调节阀门开度信号pv1。
(5)加入大小为R的干扰流量,管路中所需流量Q2 为Q1-R,得到新的流量值Q2,再次放入函数g(x) 中,得流量Q2 下的阀位pv2。
(6)前馈补偿系数为(pv1-pv2)/扰动流量大小。
1.3 阀位补偿函数设计
实验工况的改变会引起对象非线性参数的变化。在液位控制系统中,非线性参数通常存在于调节阀开度与管路流量、水箱液位与管路流量之中,即f(x)与g(x)都存在非线性。g(x)的非线性会导致前馈补偿系数的不通用,对于不同的液位、不同大小的扰动,所对应的前馈补偿系数存在差异。液位控制系统中加入阀位补偿函数如图4 所示。pv′为加入补偿阀位函数后调节阀的“虚假阀位”。未加入阀位补偿函数前g(x):pv=g(Q),阀位与流量间存在非线性;加入阀位补偿函数后g(x)′:pv′=k·Q,其中k为调节阀全开时管路最大流量的倒数,“虚假阀位”与流量间呈线性关系。对于同一个流量Q,在未加入阀位补偿函数前,阀位为pv,加入阀位补偿函数后,阀位变换为pv′,并等效更改调节阀的流量特性曲线。只要已知干扰流量大小,对于不同工况下所对应的前馈补偿系数是定值。前馈补偿器的大小为干扰流量大小除以阀全开时最大流量。
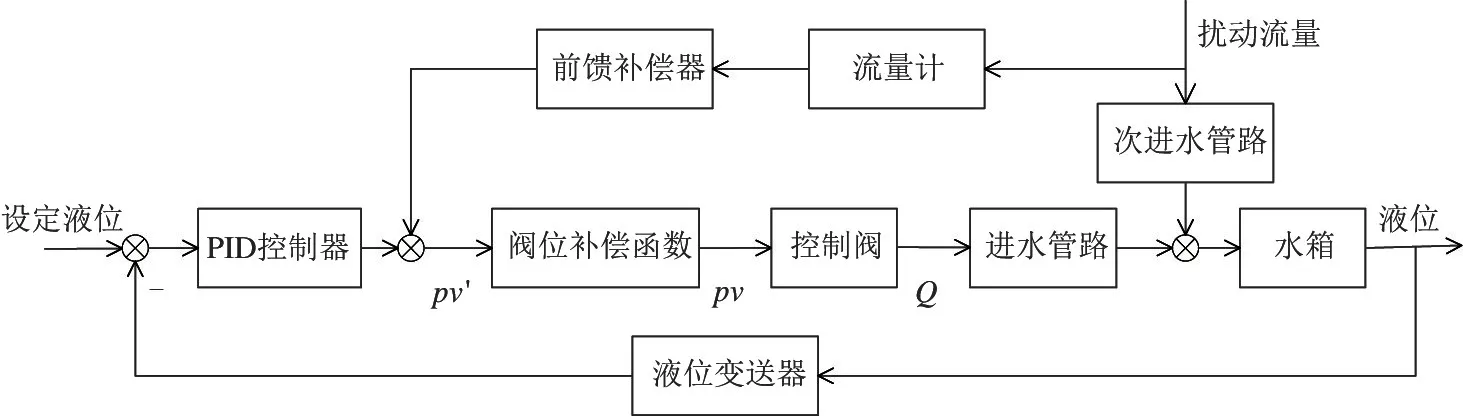
图4 液位控制系统(带阀位补偿)
2 基于Matlab 的仿真平台
2.1 硬件平台
本节对前文中所提出的液位控制系统的前馈补偿系数的确定与阀位补偿算法在液位控制实验台架上进行验证。实验装置包括主给水泵、干扰水泵、调节阀、阀前与阀后压力表、阀门定位器、阀位变送器、流量计、水箱、出水球阀以及相互连接的管道。本次数据采集设备为美国国家仪器仪表公司研发的cRIO-9030 采集机箱、信号输出板卡为NI9265、信号输入板卡为NI9203、继电器输出板卡为NI9482。采集过程的电压-电流信号,采样频率为50 Hz。液位控制系统如图2 所示,液位台架系统结构简化如图5所示。

图5 台架结构图
2.2 开环实验数据获取
为了获取各个液位(工况)稳定时的工艺参数,以便进行建模与设计前馈补偿器和阀位补偿函数,进行了开环实验。
实验步骤为:直接给阀位控制信号0~100%,待液位稳定后,记录管路中的流量Q(m3/h),水箱中的液位h(cm),阀前压力p1(kPa),阀后压力p2(kPa)。实验数据见表1。

表1 开环实验数据
根据开环实验数据求得管路和水箱的近似传递函数[20],当液位为6 cm 时近似传递函数为1.4156/76.03s+1,液位为12 cm 时近似传递函数为0.91526/98.30s+1,液位为18 cm 时近似传递函数为0.732/121.16s+1,液位为24 cm 时近似传递函数为0.47672/135.59s+1。即在不同的液位(工况)下,传递函数的增益与时间常数都存在非线性,不利于传统前馈-反馈系统中前馈补偿系数的确定。
2.3 台架建模
液位控制系统存在较强的非线性,故不采用物理建模的方式,使用工艺参数得到实验台架的仿真模型。
设定液位与实际液位进行差值计算后,送入增量式PID 控制器中。由于阀的物理特性,阀最大限度只能全开,故对PID 输出的阀位控制信号进行限幅,输出0~100%的阀位控制信号提供给调节阀的执行机构,执行机构将阀位控制信号转换成真实的阀位。阀前压力p1与阀后压力p2都与管路中的流量Q有关。由表1 可知,p1=-12.16Q2-8.278Q+57.64;p2=111Q2-4.682Q +10.14。根据流量公式Q=计算出此时管路中的流量,也就是水箱的入水口流量。出水口是一个固定开度的球阀,出水口流量大小与水箱液位有关。入水口流量与出水口流量相减后进行积分,进而得到水箱液位,完成模型的建立。Simulink 仿真如图6所示。

图6 液位台架Simulink 模型
3 仿真验证及分析
3.1 仿真实验1
根据表1 开环实验数据,得f(x),如图7 所示。
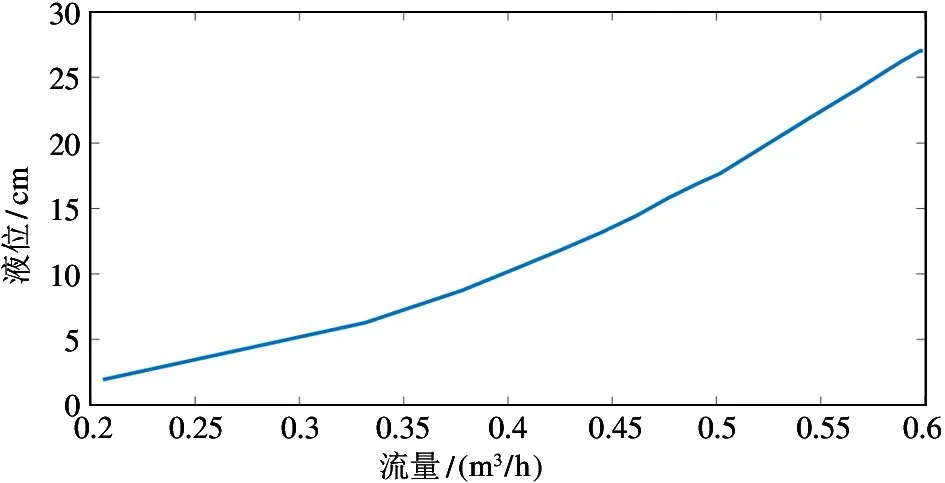
图7 流量与液位
根据表1 开环实验数据,得g(x),如图8 所示。
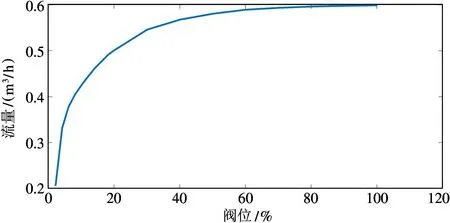
图8 阀位与流量
在阀位与流量非线性的前提下,确定前馈补偿系数。液位设定信号为12 cm 与19.5 cm,每个液位持续1000 s,干扰在600 s 加入、1000 s 消失及1600 s加入、2000 s 消失。干扰大小设定为0.085 m3/h。
当液位稳定在12 cm 时,根据f(x)与g(x)可得管路中的流量为0.428 m3/h,此时的阀位为10.3%。当干扰为0.085 m3/h 时,管路中还应提供0.343 m3/h的流量,此时的阀位为5%,阀位差为5.3%。前馈补偿系数为0.053/0.085。
当液位稳定在19.5 cm 时,根据f(x)与g(x)可得管路中的流量为0.522 m3/h,此时的阀位为20%,当干扰为0.085 m3/h 时,管路中还应提供0.437 m3/h的流量,此时的阀位为10%,阀位差为10%。前馈补偿系数为0.1/0.085。
仿真实验1 中,对于不同的液位使用相同的前馈补偿系数0.1/0.085,仿真实验1 结果如图9 所示。
仿真实验1 结论为:从图9 可知,液位为19.5 cm时,加入干扰流量后,液位没有随着扰动的加入而产生波动,前馈补偿效果良好。液位为12 cm 时,加入扰动流量后,液位发生波动,确定的前馈补偿系数为0.053/0.085,而不是0.1/0.085。前馈补偿系数过大,阀位减少过多,管路中流量减少,导致液位先下降,经过调节后达到稳定。由于开度与流量存在非线性,在某个工况下确定的前馈补偿系数并不能适用于所有的液位。
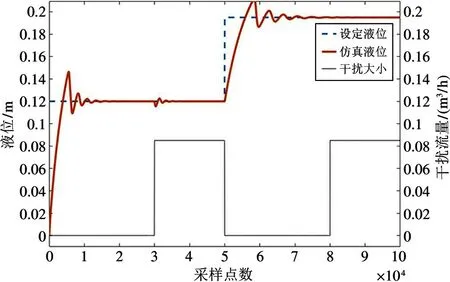
图9 仿真实验1 液位与干扰
3.2 仿真实验2
根据表1 开环实验数据,并通过流量公式Q=(Q为管路中的流量,Kv(x) 是流量特性曲线,x是阀门开度,ΔP是阀前后压差)计算该阀的流量特性曲线。结果见表2。从表1 开环实验数据中得到管路中的最大流量为0.599 m3/h。“虚假阀位”pv′与流量Q呈线性关系,故Q=0.599pv′。根据表1 可得原台架pv与流量见图10 中虚线所示,“虚假阀位”pv′与流量见图10 中实线所示。
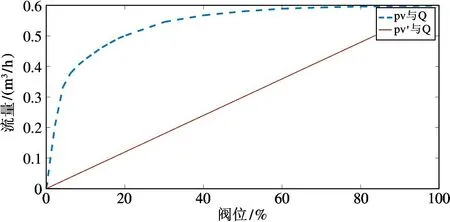
图10 阀位与流量
加入阀位补偿器后,阀位补偿器加原台架的流量特性曲线等效成新的流量特性曲线。新的流量特性曲线为pv′与Kv,如图11 所示,虚线为原流量特性曲线,实线为新流量特性曲线。具体数据见表2。
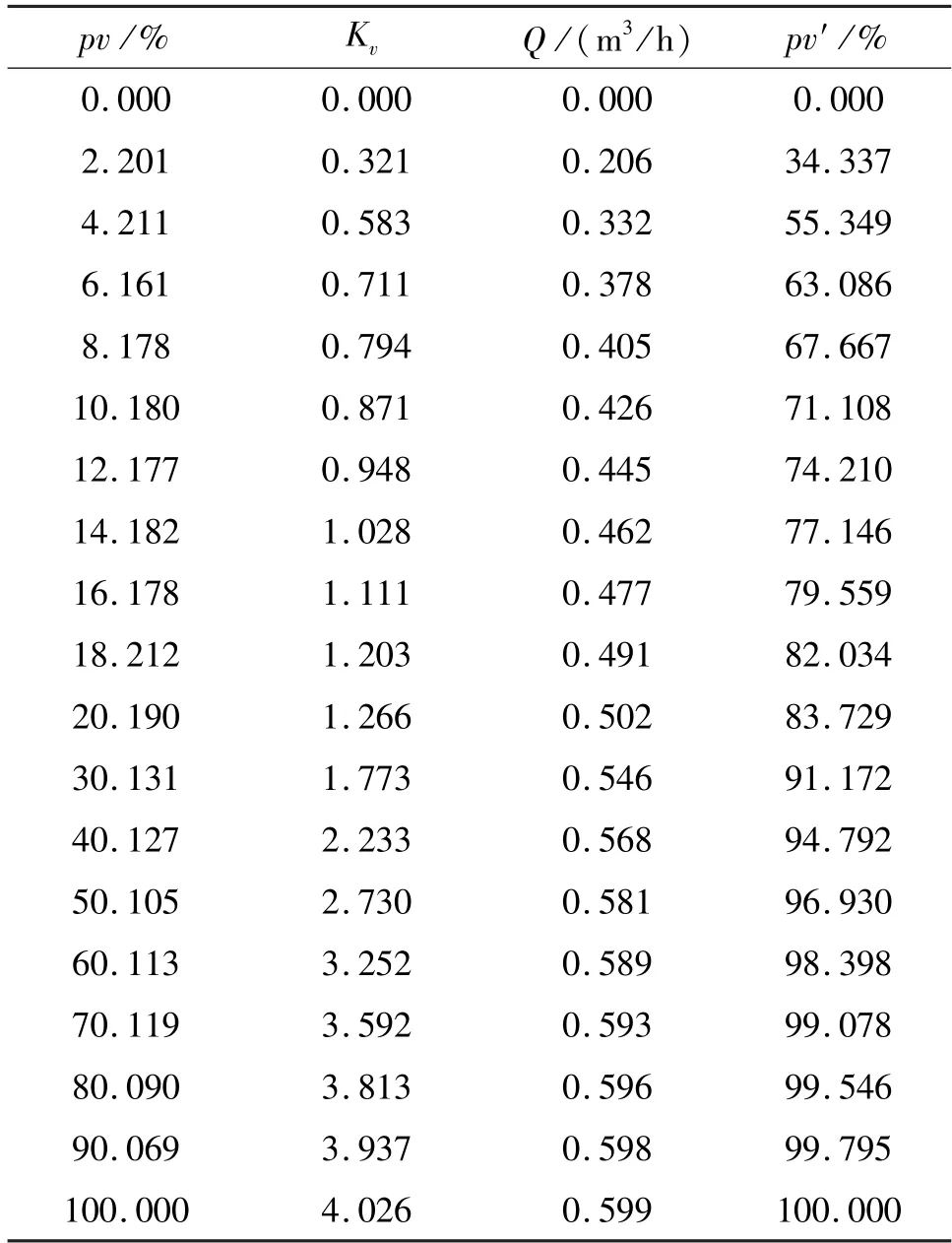
表2 阀位与流量参数值

图11 流量特性曲线
阀位与流量的补偿曲线的设计为:加入阀位补偿曲线后,pv′与流量呈线性。液位设定为10 cm 与15 cm,每个液位持续2000 s,干扰流量是可以测量的随机值。前馈补偿系数为扰动流量大小除以调节阀全开时流量。仿真实验2 结果如图12 所示。其中点划线是干扰流量大小,虚线是液位设定信号,实线是仿真液位信号。
仿真实验2 结论为:从图12 可知,加入阀位补偿曲线与前馈补偿器后,对应不同液位、不同大小的扰动,液位均能保持稳定。
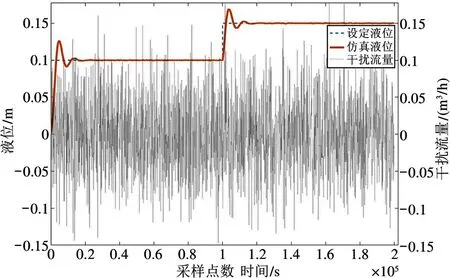
图12 仿真实验2 液位与干扰
4 现场实验及分析
4.1 现场实验1
现场实验1 实验条件为:没有加入阀位补偿函数,阀位与流量呈非线性关系。
现场实验1 的液位、干扰流量及前馈补偿系数的设定同仿真实验1。现场实验1 结果如图13所示。其中实线为实验液位,点划线为干扰流量。
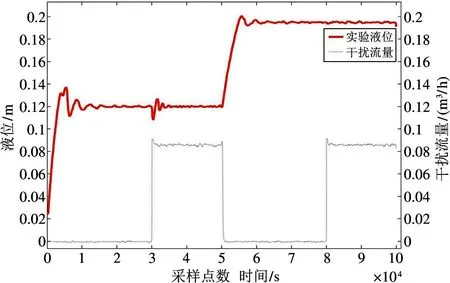
图13 现场实验1 液位与干扰
从图中可知,实验液位趋势与仿真实验1 相同,实验现象和结论与仿真实验1 相同。
4.2 现场实验2
现场实验2 实验条件为:加入阀位补偿函数,阀位与流量呈线性关系。由于实验条件的限制,只能手动调节扰动流量大小。
现场实验2-A:液位设定为15.5 cm 与22 cm,每个液位持续1500 s,干扰在1000 s 加入、1500 s 消失及2500 s 加入、3000 s 消失。前馈补偿系数为干扰流量大小除以阀门全开的流量(R/0.599)。现场实验2-A 结果如图14 所示。
现场实验2-B:液位设定为22 cm,液位持续1200 s,干扰在600 s 加入、1200 s 消失,并且干扰大小发生改变。前馈补偿系数为干扰流量大小除以阀门全开的流量(R/0.599)。现场实验2-B 结果如图15所示。
图14 与图15 中,虚线代表没有前馈补偿器有阀位补偿器的实验液位信号,实线代表加入阀位补偿与前馈补偿器的实验液位信号,点划线代表扰动流量大小。
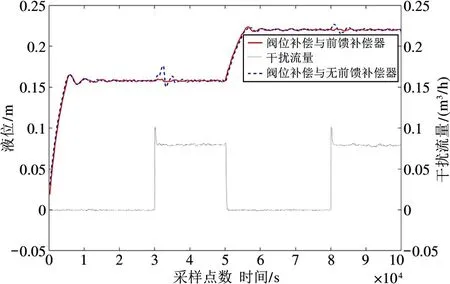
图14 现场实验2-A

图15 现场实验2-B
现场实验2 结论:从图14 和图15 可知,加入阀位补偿曲线后,使用同一个前馈补偿系数,在不同的液位,液位不随着扰动的加入而发生波动。与现场实验1 不同。并且对于同一个液位,干扰流量的大小发生改变,液位也没有发生波动。实验结论和现象与仿真实验2 相同。
5 结论
本文研究了基于调节阀流量特性曲线的前馈控制系统,利用实际工况参数与调节阀流量特性曲线来确定前馈补偿系数,而不是通过零极点配置、预测控制、内模控制及先进PID 控制等角度去分析前馈或者消除干扰的影响。并且通过大量的实验与仿真验证其有效性。由于阀位与流量间存在非线性,导致所求前馈补偿系数不具有通用性。进而提出阀位补偿算法,等效更改调节阀的流量特性曲线使阀位与流量呈线性。在所有工况下,前馈补偿系数为干扰流量大小除以阀全开时流量。阀位补偿曲线的作用不应仅局限于使调节阀阀位与流量呈线性关系,而应根据实际控制效果的需求,通过软件改变调节阀的流量特性曲线,而不是通过更换阀芯或者套筒的形式。研究结果对于实际生活生产具有一定的参考价值。

