WSN 目标跟踪场景中基于能耗约束的传感器选择算法①

王会勤 付春玲 胡振涛 刘先省 金 勇

(*河南大学计算机与信息工程学院 开封475004)

(**河南大学物理与电子学院 开封475004)

(***黄淮学院 驻马店463000)

0 引言

无线传感器网络(wireless sensor networks,WSN)是由大量微传感器构成的自组织无线网络系统,具有传感器节点小型化、成本低、容错率高等优点,已在车辆导航、灾难恢复、航空和医疗保健等领域获得广泛应用[1-4]。目标跟踪是无线传感器网络最重要的应用之一,由于传感器节点传感、通信和计算资源有限,采用合理的传感器管理方法可在保证跟踪精度的同时降低WSN 能耗[5-6]。

为了减少通讯传输的能量消耗,文献[7,8]通过对传感器接收到的数据进行压缩量化,将条件后验克拉美罗界(conditional posterior Cramér-Rao lower bounds,CPCRLB)作为节点选择的优化准则,激活最优传感器节点进行目标跟踪任务。在监测概率约束的节点观测模型下,文献[9]将工作的传感器节点测量数据量化,提高目标观测精度。但是由于对原始监测数据进行了量化压缩,目标轨迹估计没有利用实际观测信息,因此该方法难以直观描述选择传感器的跟踪性能。文献[10]采用簇头随机选择方法,构建动态分簇结构,并适时调整分簇策略,降低WSN 总能耗,但该方法难以保证WSN 能量均衡。文献[11,12]以测量误差协方差矩阵迹为目标函数,将惩罚项描述为节点选择矩阵列数与节点选择次数的和,利用交替向量乘子法来解决此优化问题,但运算复杂度较高。文献[13,14]利用扩展卡尔曼滤波算法(extended Kalman filter,EKF)最小化估计误差,该方法以测量误差协方差矩阵的迹为目标函数,以卡尔曼增益矩阵的列为惩罚稀疏项,通过构造等式约束和增广拉格朗日函数,利用交替向量乘子法求解,但该方法未考虑WSN 能量均衡且运算复杂度较高。

针对上述问题本文提出一种基于估计精度和能耗约束的WSN 目标跟踪传感器选择算法,以估计协方差矩阵的迹和传感器量测能耗函数之和为目标函数,以传感器量测能量阈值为约束条件,将卡尔曼滤波增益矩阵及传感器量测能耗矩阵为待优化变量,解决WSN 目标跟踪过程中的传感器选择问题,平衡网络的估计精度和能量消耗。

本文对使用符号的定义如下:大写粗体字母如F表示矩阵,小写粗体字母如x表示向量,‖·‖2表示向量的2 范数,1 表示全1 向量或矩阵,[·]T、[·]-1分别表示矩阵或向量的转置和矩阵的逆,tr(·)表示矩阵的迹,▽为一阶导数算子运算,card(·)为集合势。

1 问题描述

考虑图1 场景模型,在大小为A×A的二维监测区域内,随机分布M个静止传感器节点,选择部分传感器节点在时间T内对沿区域对角线匀速直线运动的目标进行跟踪,假设每个传感器节点都能够选择开启测量目标位置。

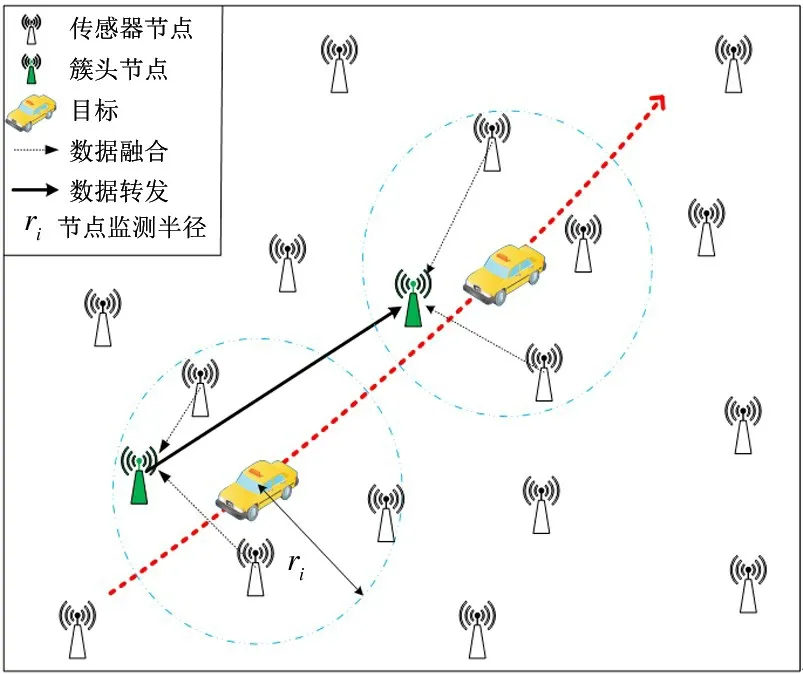
图1 场景模型图

在t=1,…,T时刻,目标状态可由四维状态向量xt=[x(t),y(t),vx(t),vy(t)]T表示,其中x(t)和y(t)分别表示t时刻目标在水平与垂直方向上的位置坐标,vx(t) 和vy(t) 分别表示t时刻目标在水平与垂直方向上的速度值。假设目标运动模型如下:

其中,F为运动状态转移矩阵,ωt为均值为零、协方差矩阵为Q的加性高斯噪声,且

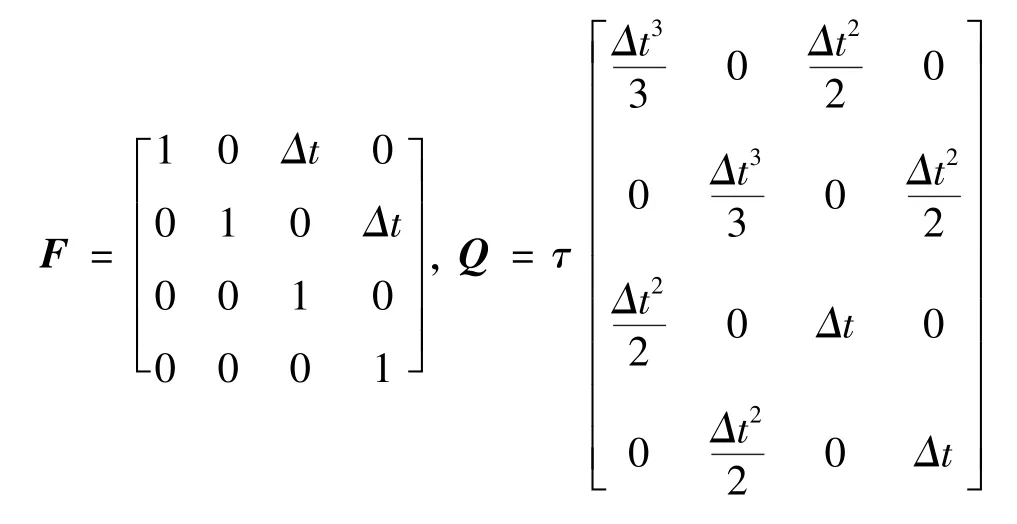
式中,Δt是测量时间间隔,τ为过程噪声参数。

假设节点i的位置坐标为mi=[xi yi]T,有效监测覆盖面积为以节点位置为圆心、半径为ri的圆形区域。当目标出现在节点的有效监测覆盖范围内时,就可以获得目标与监测节点的距离信息。假设目标在t时刻的位置坐标为Lt=[x(t),y(t)]T,则t时刻节点i和目标间的距离为

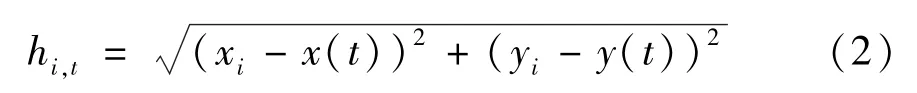
即当hi,t≤ri时,且传感器节点i剩余能量高于剩余能量阈值Esur时,传感器节点i作为候选节点,可选择开启进行目标测量。随着目标运动,目标移动出传感器节点感测范围,hi,t ＞ri时,传感器节点停止监测目标任务,进入休眠模式。不失一般性,本文假设所有传感器节点有效监测覆盖面积相等。

2 传感器管理优化算法

在传感器网络目标跟踪系统中,合理高效的传感器管理方法可在保证跟踪精度的同时降低WSN能耗。而采用多跳方式,利用簇头转发数据能有效降低网络内节点能耗,起到延长网络寿命的作用[15]。本文所提传感器选择流程如图2 所示。

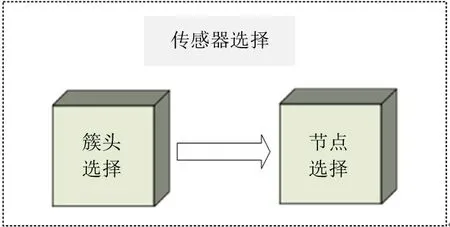
图2 传感器选择流程框图

2.1 簇头选择

为了提高目标的跟踪精度及节省网络能量消耗,本文采用动态选择簇头的方法。当目标开始进入监测区域内时,由于获取的目标信息较少,跟踪误差较大,因此此时选择簇头节点时优先考虑能耗因素,选择距离目标最近的传感器节点作为簇头节点,进行工作节点的测量数据收集和融合,减少传感器节点的数据转发能耗与簇头收集数据能耗。然后工作传感器节点利用EKF 滤波算法进行目标状态估计,簇头收集工作传感器节点对目标的估计状态,并将状态估计信息转发给下一簇头。随着目标运动,当此簇头节点移动出目标被监测范围时,选择下一簇头。定义预测簇头能量函数公式如下:

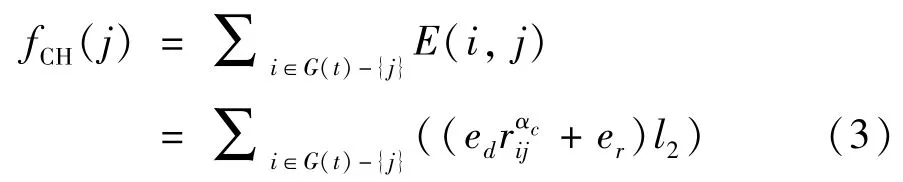
其中,G(t) 为t时刻的候选工作节点集合。若传感器节点j选为簇头,则其余传感器节点i(i=1,2,…)card(G(t)) -1 转发数据到簇头j的总能量为fCH(j),rij为传感器节点i到传感器节点j之间的距离,αc为已知路径衰减因子,l2为转发数据大小,er为接收1 位数据的能耗,ed为传感器节点j决定的已知路径能量特性。

因此为了节省网络能耗,应选择预测簇头能量最少的传感器节点作为簇头节点,以使传感器节点进行转发数据、簇头收集数据的能量最小,即选择t时刻的簇头节点为

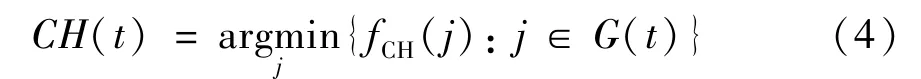
2.2 节点选择

假设传感器节点在测量过程中受到扰动噪声干扰,则t时刻的N个候选传感器节点对目标的测量可表示为

其中ψt是测量噪声,假设其为零均值的高斯噪声,协方差矩阵R=σ21N×N。

由于本文观测模型是非线性的,因此采用EKF进行目标状态估计。在EKF 预测阶段,计算状态一步预测值:

求解一步预测状态协方差阵:

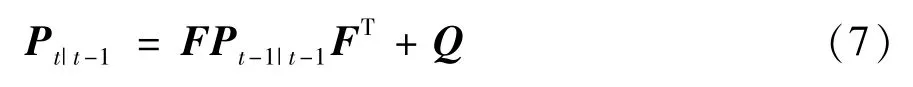
更新阶段,首先对非线性系统模型进行一阶泰勒展开,Ht=是测量函数h(·)在时间t上关于预测状态的联合雅可比矩阵。

更新协方差矩阵:

计算滤波增益:

为了节省网络能耗,应选择较少的工作传感器节点进行目标跟踪,且为了得到较高的跟踪精度,本文以后验估计协方差矩阵Pt|t的迹tr(Pt|t) 最小为目标函数,其中估计协方差矩阵Pt|t=(I-KtHt)Pt|t-1,以卡尔曼增益为优化问题的解,目标函数为

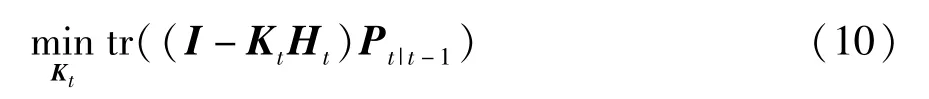
式(10) 仅在选择节点个数方面进行优化以节省能耗,而选择目标监测过程中使用能量较少的节点可以更有效地节省网络能量消耗。假设量测单位目标状态变化量需要量测能量‖e‖2,e=(ex,ey,evx,evy)T,其中ex、ey和evx、evy分别表示位置和速度的量测能量分量,且ex=ey=2evx=2evy。约束传感器节点i测量目标状态变化所用的能量不高于传感器节点用来量测目标的可用参考能量(E0)i,E0∈RN,超出参考能量的额外能量表示为Ei,Ei∈RN。因此将式(11)添加到式(10)的约束条件中:

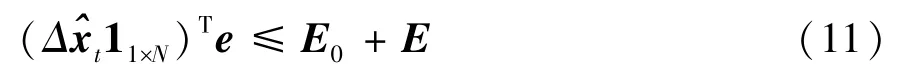
其中,

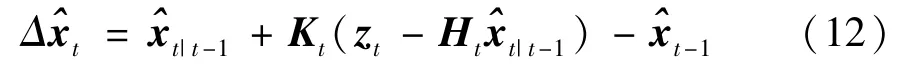
是t时刻与t-1 时刻的目标估计状态变化量,为t时刻目标状态预测向量。显然应该避免消耗传感器节点的额外能量,因此有必要在式(10)的目标函数中添加与额外能量相关的惩罚项,于是优化问题式(10)表示为如下形式。

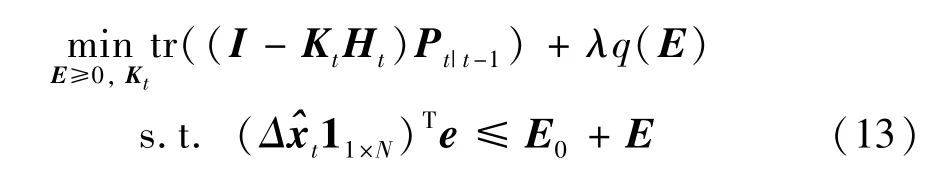
惩罚函数q(·)=‖·‖2,λ为正则化参数。当选择工作的传感器节点产生额外能量E时,消耗的E越多,则对目标函数的惩罚越大,即目标函数值越大,表示此选择的工作传感器节点不是所求最优选择方案。相反,具有最少能量消耗的最少选择传感器节点个数的方案,其目标函数最小,可平衡精度和能量消耗。

由于式(13)中目标函数和约束条件都为凸形式,因此本文问题式(13)为标准凸问题,可以利用凸优化工具包直接求解,其计算复杂度为O(N3)[16]。

3 仿真结果与分析

与仿真有关的场景和参数分别如图1 和表1 所示。本文算法在位置均方根误差(root mean square error,RMSE)和网络累积消耗能量方面与文献[4]、文献[9]、文献[14]中的算法进行了对比。簇头和节点的能耗模型和参数均与文献[17]一致。RMSE公式如下所示:

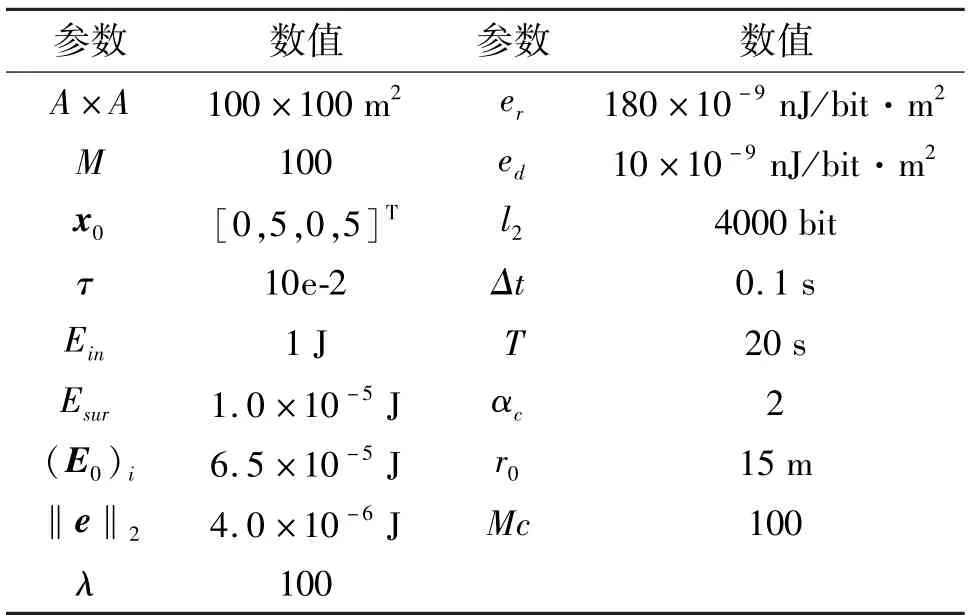
表1 仿真参数设定

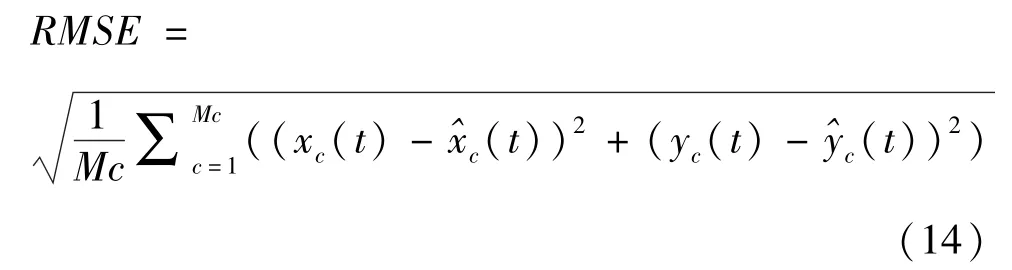
其中Mc为蒙特卡罗仿真次数。

RMSE 随时间变化对比图如图3 所示。从图3可以看出,当开始利用传感器节点进行监测时,所有算法的误差都较大,RMSE值较高,估计精度较差。随着目标运动,采样次数逐渐增加,所有算法的RMSE降低,估计精度增加。本文所提算法由于监测范围约束,选择传感器节点与其他算法相比距离目标显然较近,量测误差较小,在大多数监测时间内的RMSE值较其他算法低。

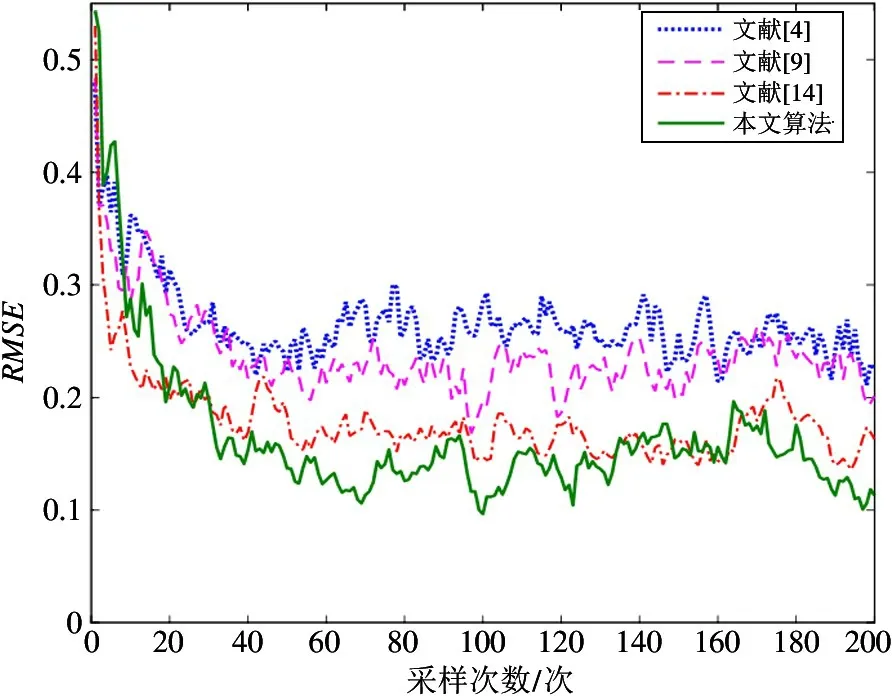
图3 RMSE 对比

为了验证所提算法节省能耗的有效性,本文在网络累积消耗能量方面与其他算法进行对比,结果如图4所示。

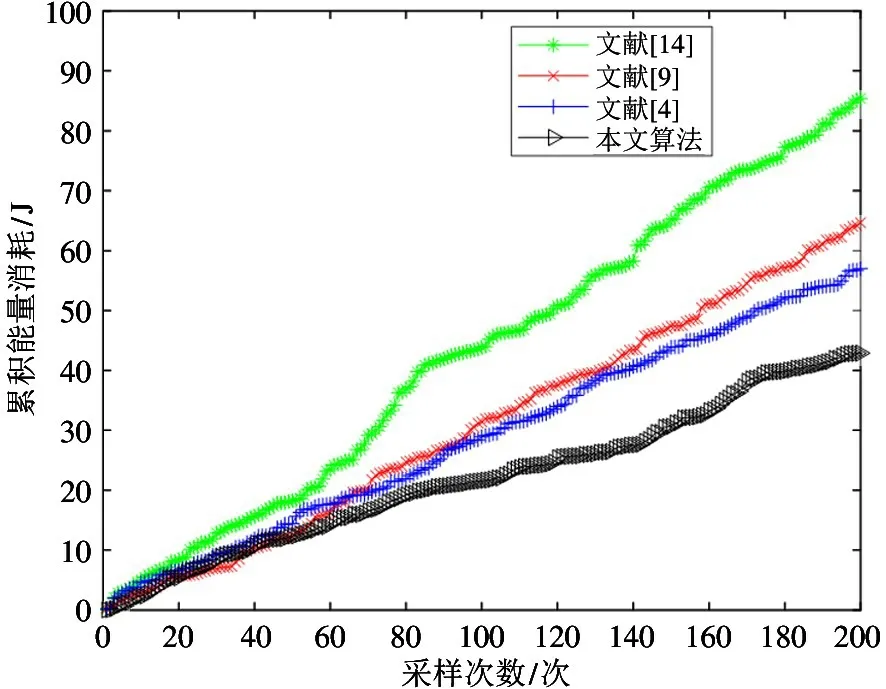
图4 累积能量消耗对比

所有算法初始网络总能量均为100 J。当运行时间相同时,本文所提算法的能量消耗低于其他3种算法,剩余能量高于其他算法。这是由于转发数据能耗是无线传感器网络的主要能量消耗,且转发能耗随距离呈正相关关系,而所提算法转发数据仅在监测范围内进行。随着运行时间增加,4 种算法的网络能耗都逐渐增加,对应的累积能量消耗曲线都在不断上升,剩余能量不断减少。当运行时间结束时,所提算法与其他3 种算法相比能量消耗最少,剩余能量最多,相比其他算法,本文算法有效地节省了网络能耗。

为了准确分析所提算法的传感器节点能量使用情况,本文在传感器节点剩余能量分布情况方面进行了分析。结果如图5 和图6 所示。

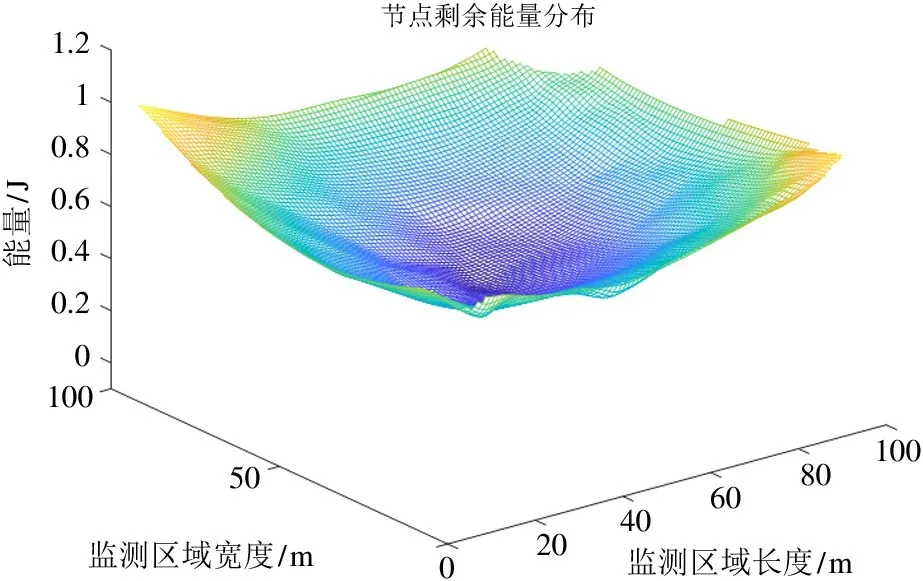
图5 剩余能量分布

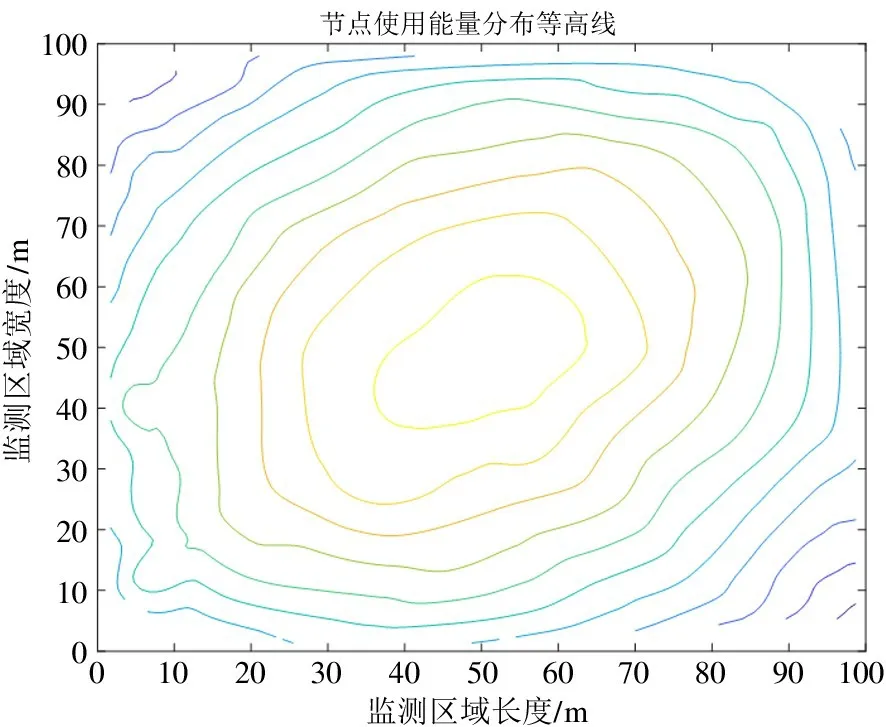
图6 能量分布等高线

从图5 可以看出,由于进行目标测量和数据转发,在目标运动轨迹附近的传感器节点剩余能量比距目标轨迹较远的传感器节点少,使用能量多,其使用能量分布等高线如图6 所示。由于监测范围约束,传感器节点进行数据转发时距离较短,因此整个网络运行中转发数据能量平均较小,实现了能量均衡。

4 结论

针对WSN 中利用传感器节点进行目标跟踪过程中的能量优化问题,本文提出了一种基于能耗约束的传感器选择算法,以估计协方差矩阵的迹与传感器量测能耗函数的和为目标函数,以节点量测能量阈值为约束条件,将卡尔曼滤波增益矩阵和能耗矩阵作为问题的解,解决了WSN 目标跟踪过程中的传感器选择问题。同以往的算法相比,本文所提算法能节省网络能量,实现网络能量均衡。未来的工作将致力于研究多个目标运动时传感器节点选择,以便提高无线传感器网络的节点利用率。