磨辊堆焊修复路径规划
周奥博,王微伟,王喜临,刘爱国
(1.沈阳理工大学, 沈阳110159;2.江苏瑞米克金属技术有限公司,江苏 常州 213172)
0 前言
20世纪60年代以来,为提高能源利用率,越来越多的火力发电厂采用中速磨煤机[1-2]作为制粉系统的磨煤工具。中国出产的煤种类繁多、杂质含量高、可磨性非常差,再加上工人经验不足,导致磨煤机磨辊、磨盘过快地磨损。为了降低生产成本,采用焊补的方式对磨损缺口进行修复。目前国内大多数发电厂主要依靠于人工焊补。但是人工焊补存在着许多问题例如效率低、焊接质量差、工作环境差以及弧光污染、粉尘污染对工人健康的影响等。采用智能焊接机器人进行焊补是解决该问题的有效方法。对于不规则的磨辊磨损缺口,焊道的路径规划是开发磨辊磨损缺口智能修复系统要面对的首要问题。现阶段,大型结构件的焊道路径规划[3-5]应用于规则的焊接坡口,如V形坡口、单边V形坡口或者在平面上进行焊道路径规划堆焊的增材制造技术。中厚深度的结构件焊缝填充策略一般有3种:①等高型焊缝填充策略[6-7],每一层高度相同,且遵循焊道数目与所在层数相等的原则,由于焊接面积不同,需要在焊接过程中频繁改变焊接工艺参数,导致精度上难以控制;②等面积焊道填充策略[8]在保证每一层所具有的焊道数与层数相等的前提下每一条焊道的截面积相同,此方法虽然焊接参数相同,但焊道的路径规划更加复杂;③自定义型填充策略[9-13],首先在离线规划系统中设置焊道的焊接工艺参数、焊接顺序、规划类型等,系统再利用这些信息自动规划焊接路径和姿态,从而进行焊道排布。由于磨辊堆焊修复缺口较大,而且是在不规则凹陷区域进行堆焊,所以无法遵从每一层焊道数与层数相等的原则,无法利用现有的填充策略实现焊道路径规划。
文中在等高型和等面积型焊缝填充策略的基础上自定义焊缝填充策略,进行磨辊堆焊修复路径规划研究。并且利用由三轴焊接机械臂和可自转、可绕转轴转动的磨辊所组成的堆焊系统,进行路径规划结果的运动控制。
1 焊缝填充策略
结合目前焊接路径规划资料及实际生产需要,文中在等高型(图1)和等面积型焊缝填充策略的基础上自定义焊缝填充策略:每一层焊接高度与焊道长度不变,即单条焊道的余高与路径规划中任意两焊接目标点的距离不变,在焊接工艺参数不变的前提下,每一层的焊道数目由填充焊道长度、截面积和缺口每层底边长度、每层面积确定。
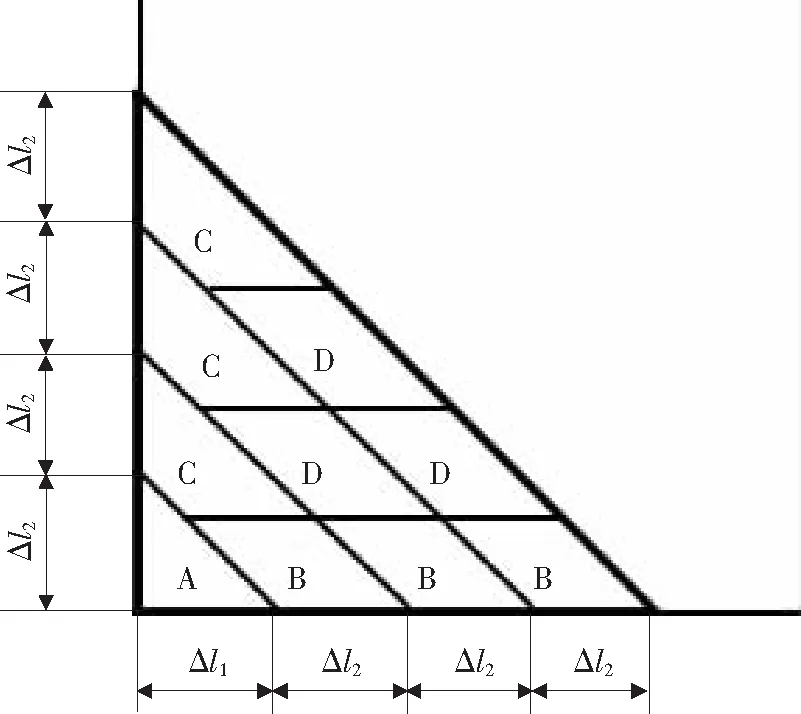
图1 等高型焊缝填充策略
采用激光扫描、图像处理或接触测量等方法得到磨损磨辊的外部轮廓,再将其尺寸与完整磨辊的尺寸进行对比,得到待焊区域如图2所示,实线线条为磨损磨辊的外部轮廓,虚线线条为完整磨辊外轮廓,填充部分为磨辊缺口待焊区域。
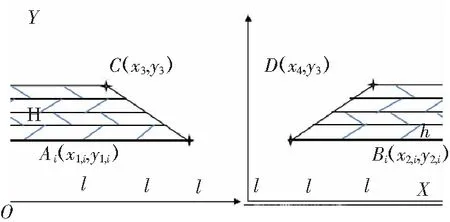
图2 磨损磨辊的尺寸采集示意图
采集待焊区域底部轮廓点进行数据分析。采集到的底部轮廓点转换为基坐标系下的坐标值,采用斜率分析法找出符合要求的拐点,方法如下:设任意点pi(xi,yi),pi点右边斜率为kr,pi点左边斜率为kl,则:
(1)
(2)
Δk=|kr-kl|
(3)
若Δk>Δki-1,且Δk>Δki+1,则pi为拐点。通过此方法可以除去一些表面不是很平整的假拐点,从而得到缺口形状,如图3所示。通过斜率分析法将缺口不规则截面化成简单梯形进行焊道规划,梯形可满足大多缺口形状近似的要求。
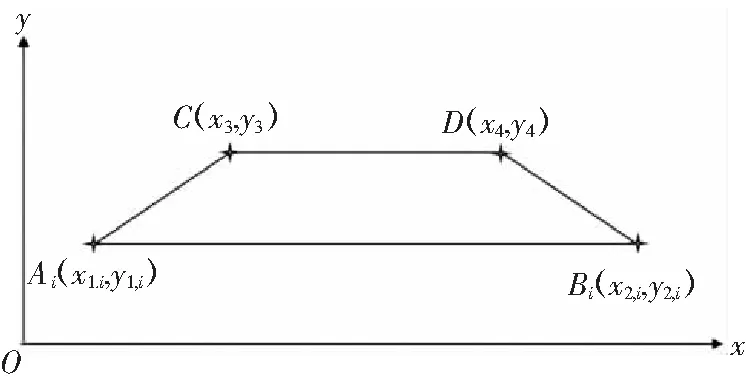
图3 斜率分析法得到的规则梯形
在等高型和等面积型焊缝填充策略的基础上找出了适合磨辊堆焊修复的焊缝填充策略。每一层焊道高度一致,焊脚增长量l不变,经计算得出的每层焊道数目作为堆焊一层结束的判断依据。为保证计算结果更加准确,从而更好地修复缺损口,每焊完一层便会重新测量数据。
焊道层数的确定:梯形的高度为H,每条填充焊道的长度为l,余高为h。
填满梯形总层数n,填充焊道高度h,n取大于n的最小整数nZ。
(4)
第i层道数的确定:设填充焊道层数的序号为i,Ai点与Bi点的距离为Li。
(5)
由第i层底边长度Li计算焊道数目:
(6)
将其整数部分记为Ni,小数部分记为Ci,焊道数目由小数Ci确定,即为保证每层最末焊道有适当的熔宽,现取0.4为临界值:
若Ci≥0.4则第i层焊道数目Ri=Ni+1;
若Ci<0.4则第i层长方形焊道数目Ri=Ni。
磨辊磨损缺口路径规划结果如图4所示。
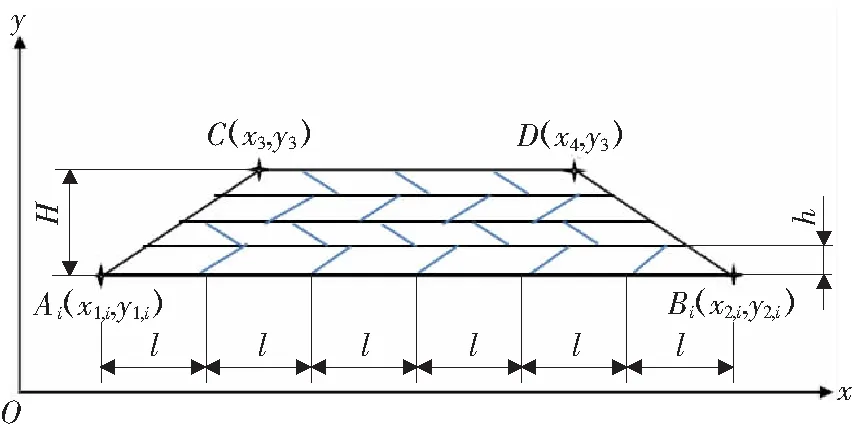
图4 磨辊焊接路径规划结果示意图
2 联动机构公式
如图5所示,磨辊堆焊智能修复采用的焊接机器人为三自由度焊接机器人,由三轴焊接机械臂和可自转、可绕第一轴O1转动的磨辊组成。磨辊自转方向如图6所示。磨辊堆焊智能修复的机械运动问题属于焊接机器人机构与磨辊机构的联动问题,磨辊的第一轴O1要与焊接机器人的第二轴O2和第三轴O3同时运动,共同完成堆焊轨迹运动。一旦目标点确定,需要同时计算三个轴所转角度,并转换成脉冲数,发送给控制转轴的两相进步电机。
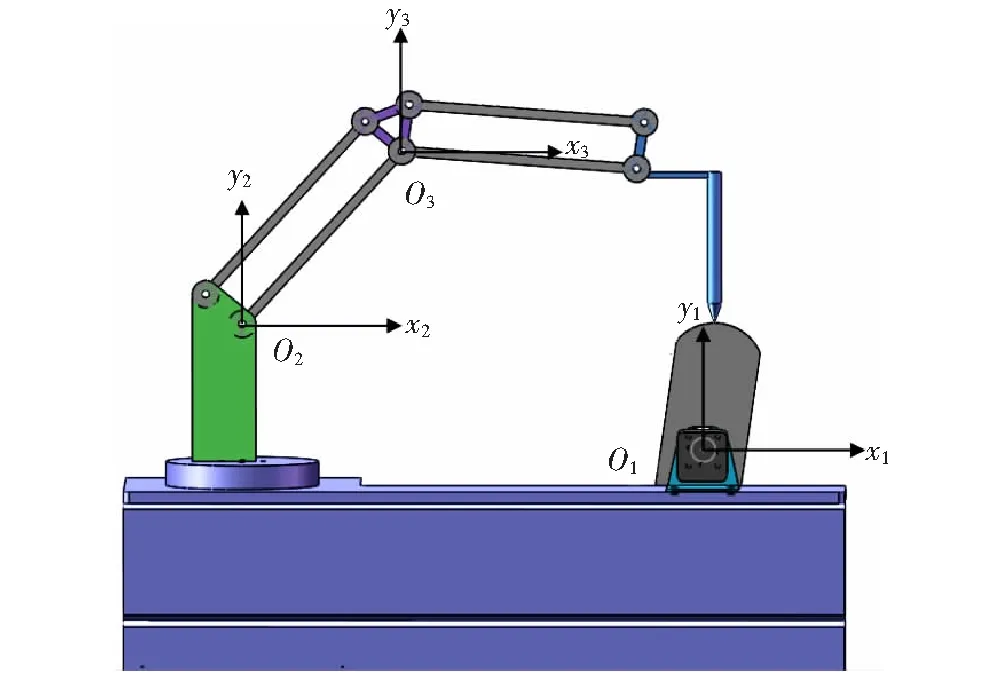
图5 磨辊堆焊系统示意图
图6 磨辊自转方向示意图
2.1 机械臂转轴公式推导
磨辊堆焊机器人[14]为三自由度焊接机器人小臂执行端(焊枪)垂直向下90°。采用D-H法建模,建立连杆坐标系,此方法可以将三维转换为二维,消除某一轴上的变量,达到简化坐标公式的目的。并且在此过程中加入齐次变换规则。具体方法如下所述。
坐标系0:取第一关节轴线与第二关节轴线的公垂线在一轴上的交点,且在第一轴中心为坐标系0的原点,关节轴线方向为y0轴的方向,如图3所示,x0轴方向为第一关节轴线与第二关节轴线的公垂线,由原点指向第二关节轴,z0轴由右手定则确定。
坐标系1到坐标系3遵循取关节轴线i与i+1的公垂线在i的交点为坐标系i的原点,zi轴方向为关节轴线方向,xi轴方向为第i关节轴线与第i+1关节轴线的公垂线,由原点指向第i+1关节轴,yi轴由右手定则确定。
根据上述模式用下列旋转和位移,可以建立相邻坐标系关系[15]:
(7)
式中:i-1Ai为描述坐标系i相对于坐标系i-1的变换;θi为描述连杆绕zi轴转动角度;αi为描述连杆绕xi轴转动角度;li为描述连杆长度;di为描述同一坐标原点移动的距离。
三自由度焊接机器人的连杆关系见表1。
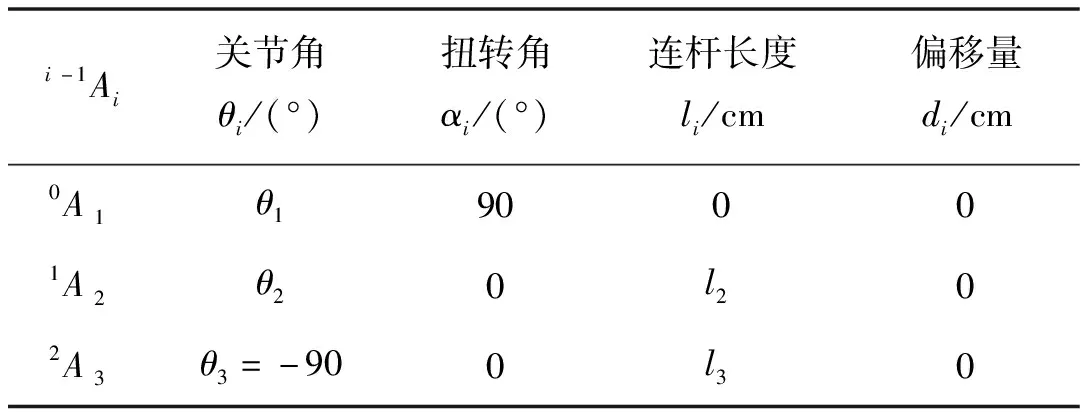
表1 连杆坐标系相关变量
将表1连杆坐标系的相关变量代入变换矩阵i-1Ai中,分别求得坐标系i相对于坐标系i-1的变换矩阵,再根据末端执行器T3矩阵与A矩阵的关系联立求解θ2,θ3,T3矩阵与A矩阵的关系如下:
(8)
(9)
(10)
由上述过程可以计算出到达任意目标点三自由度焊接机器人每轴所转角度,转换成脉冲数发送给两相步进电机。
2.2 目标点公式推导
焊接机器人机构给定目标点,求第二轴O2、第三轴O3转动角度的公式已推出,下面进行第一轴O1转动角度的推理和目标坐标点的确定。
堆焊系统机械结构简图如图7所示。由于磨辊很大,并且R2,R3对应的弧长很短,所以可以将R2,R3所对应的弧长都归为R1所对应的弧长,即弧面所对应的半径均是R1。为保证焊枪垂直于焊接点,焊枪中心线与R1的圆心共处于一条直线上,并且垂直于工作台。其中:LA=391.5 cm,LB=31 cm,LC=40 cm,LD=200 cm,LE=200 cm,LF=5.5 cm,LG=66 cm,LH=131 cm,H1=117 cm,H2=30 cm,α=39.19°,β=80.81°,R1=42.5 cm,R2=R3=10 cm,D=132 cm,B=72 cm。
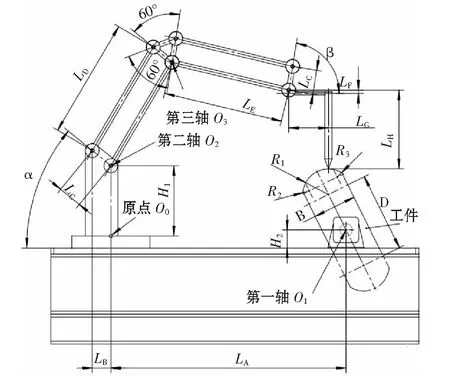
图7 堆焊系统机械结构简图
由图7可知,当焊枪位于磨辊连接点A时,第一轴O1转动角度为26°,位于连接点B时,转动角度为154°。设第i层除A点外有4个焊接点,如图8所示,第i层中心点到以R1为半径弧的距离为hi,0。
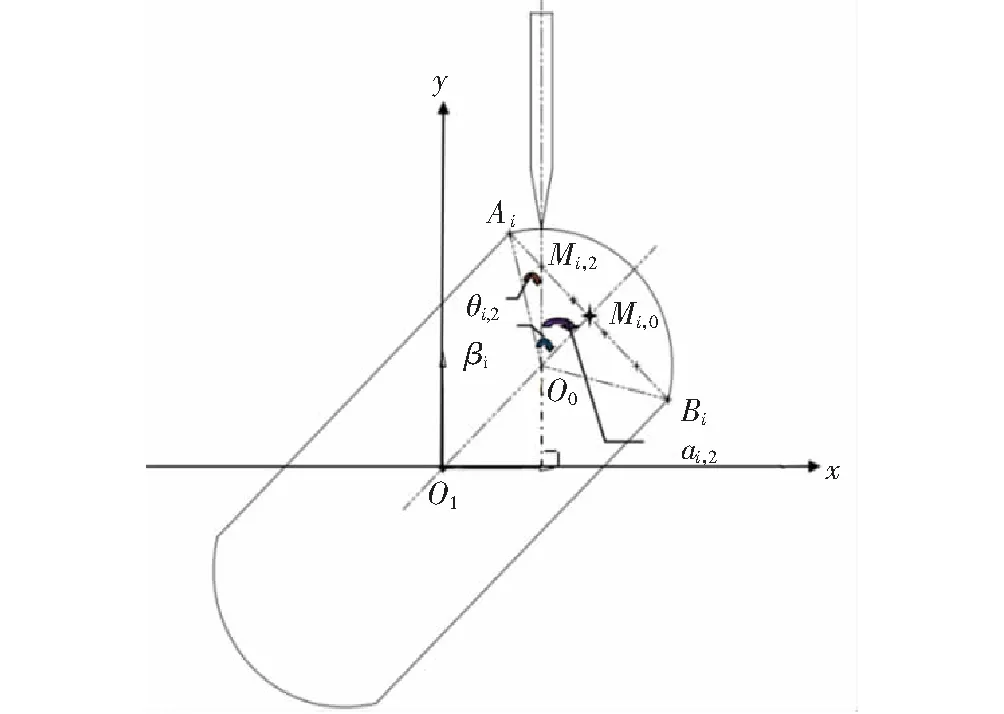
图8 第i层第二个焊接点
根据结构的几何关系有:
(11)
(12)
|O0Mi,0|=R1-hi,0
(13)
(14)
(15)
θi,2=βi-αi,2
(16)
式中:Mi,0为AiBi的中心点;Mi,2为第i层第二个焊接点;βi为第i层∠AiO0Mi,0的角度;αi,2为∠Mi,2O0Mi,0的角度;θi,2为∠AiO0Mi,2的角度。由相似三角形关系,可得第i层第二点的坐标Mi,2如式(17)所示;剩余3个焊接点重复式(10)~式(15),经分析推理得到任意点坐标Mi,j(i≥表示第i层;j>1表示第j个焊接起始点)如式(18)所示。
(17)
(18)
2.3 磨辊转轴公式推导
任意坐标点与第一轴转动角度的关系可由表2推出。

表2 第一轴O1的R1特殊点角度
设堆焊系统机械结构的焊枪初始位置左连接点到中点此时R1的圆所对的圆心角为57.89°,第i层最初起始点A到中点此时R1的圆所对的圆心角为βi,则左连接点到第i层最初起始点A此时的圆所对的圆心角为(57.89-βi)°。根据表2里对应的比例关系,从左连接点开始到目标点与R1圆心延长线在圆弧上的交点,焊枪轨迹所对应的弧长,其R1的圆心角每增加1°第一轴转动角度增加1.11°,如从左连接点到A点半径R1的圆所对的圆心角为(57.89-βi)°,则第一轴共转了[1.11*(57.89-βi)+26]°。
3 仿真模拟分析
为验证磨辊堆修复路径规划的可行性,基于MATLAB软件对规划好的路径进行仿真模拟[16-17],模拟出堆焊路径。首先,根据D-H法和辊套堆焊结构建模,设置关节角度、关节距离、连杆长度、连杆转角、关节类型等,建立三自由度焊接机器人的仿真模型,如图9所示。然后,输入测量变量A,B,C,D 4点及单条填充焊道长度和高度,画出预计修补范围,并计算限制条件焊接层数与每层焊接道数。接着输入第i层初始测量点和,即可得到焊接路径仿真规划轨迹及焊枪在任意两点之间的位移、速度、加速度变化曲线,如图10和图11所示。图10是焊枪仿真轨迹和由实际测量焊枪在磨辊磨损缺口位置数据绘制的轨迹对比图。由于磨辊尺寸、测量误差及计算时的精确度导致两轨迹图不能完全重合,但两图走势规律一致并且只有少数未重合点说明该路径规划推理是正确的。由图11可知,机械臂从任意中间点A到下一点的过程中,焊枪末端位移曲线平滑无奇异点说明机械臂可稳定地实现空间运动,并且A点处的速度、加速度从零开始,B点处的速度、加速度减至为零,说明机械臂可以稳定地启动和停止,进一步说明了文中路径规划推理的正确性。
图9 三自由度焊接机器人的仿真模型
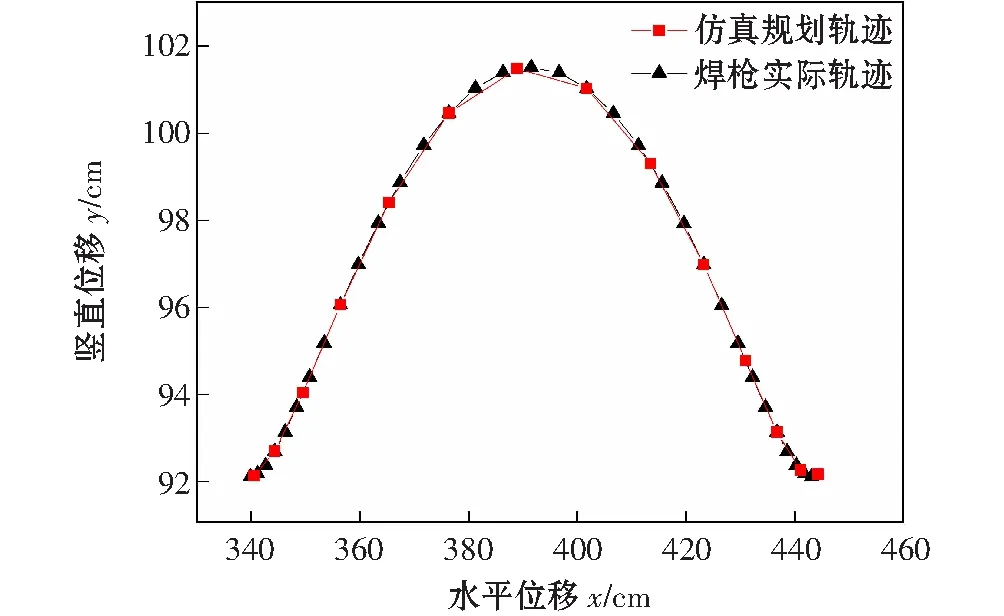
图10 焊枪路径轨迹图
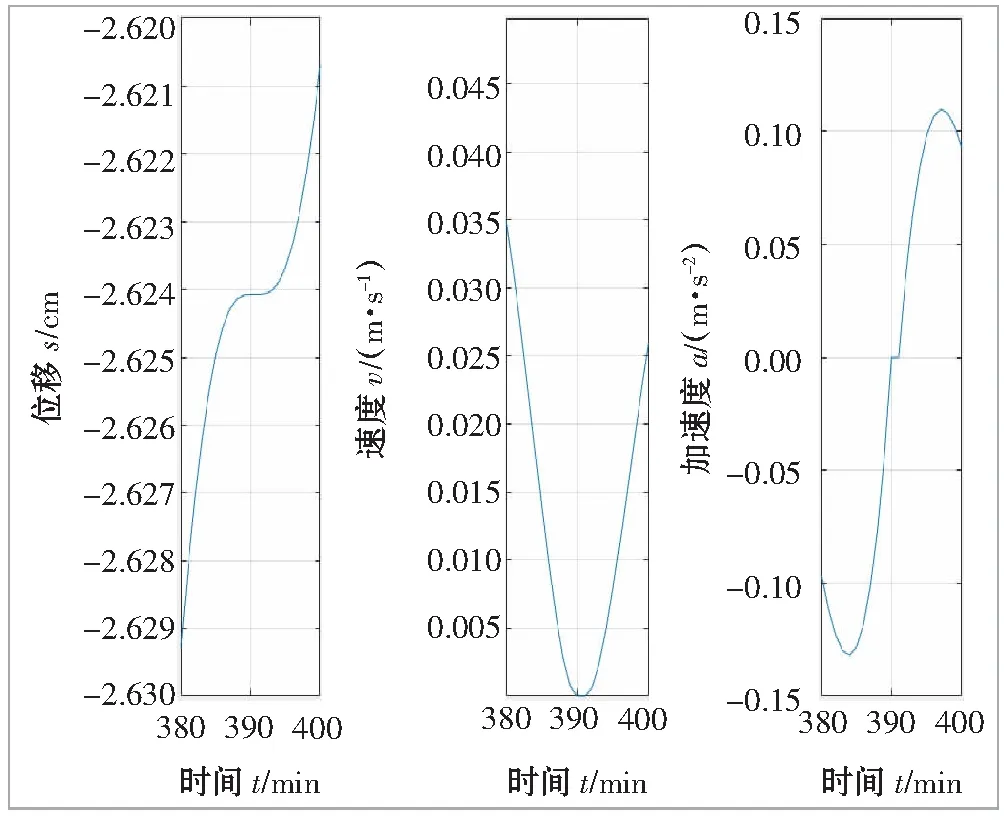
图11 焊枪末端位移、速度、加速度
为验证路径规划算法及仿真试验的合理性,基于堆焊系统机械结构搭建了三自由度模拟焊接机器人系统:硬件包括三自由度焊接机器人、控制器、上位机如图12所示,软件包括基于C#语言和上述推理得到的路径规划算法所开发的自动规划焊道路径软件如图13所示。在模拟焊接机器人系统中输入与仿真系统的相同坐标值和变量参数,利用上位机控制软件的暂停继续功能进行模拟的实际焊接轨迹的位置测量,得到的实际焊接轨迹如图10所示。

图12 三自由度模拟焊接机器人系统硬件

图13 路径规划软件控制界面
4 结论
在等高型和等面积型焊缝填充策略的基础上提出了改进的磨辊堆焊焊缝填充策略,进行了磨辊堆焊焊道路径规划,并进行了焊接机械臂末端的运动学仿真。仿真结果证实了焊道路径规划的合理性,机械臂可以平滑稳定地到达路径规划后的任意一点,机械臂可以稳定地启动和停止。

