弹体冲击下测量光束的偏摆修正研究

田森,段小艳,张大治,李新良,贾志婷,姜延欢

(航空工业北京长城计量测试技术研究所,北京 100095）

0 引言

激光干涉仪作为冲击校准装置的标准量值传递设备,在科研院所和高校广泛应用,其最大测量速度为30 m/s,可实现冲击速度、加速度等量值的可靠溯源和准确复现。但随着武器装备的升级和仪器的精密化发展,现有校准设备已不能满足100 m/s强冲击试验装置冲击速度校准的需求[1],这主要是因为系统的性能不足,如在高冲击速度情况下,衍射光栅的结构强度和粘附强度会受到一定削弱,且在实际测量过程中很难保证高速运动目标做直线运动,砧体受到碰撞将会发生偏摆,固定于砧体上的光栅则随之发生角度运动[2],会导致采集数据的丢失以及测量结果精度偏低。

光栅具有体积小、损耗低、耐腐蚀、易于组网等特点,被广泛应用于光束测量试验中。国外在80 m/s以上的冲击测量试验中发现,随着冲击速度的提升,发生光栅脱落或变形的概率会升高,不仅会浪费时间成本和经济成本,还会造成数据缺失甚至试验失败。为满足强冲击试验装置在100 m/s下的校准需求,需做到以下两方面:①需要深入优化衍射光栅的自身结构强度和粘接工艺,提高冲击测量试验的效率。特别是在高速冲击条件下,运动结构具有复杂的动态响应[5],碰撞过程中砧体姿态的变化和剧烈摆动也会降低光电信号的稳定性,影响数据解算准确度[3];②需要通过降低测量光束的偏摆角度[4],使其在一定范围内,从而使干涉光斑不会脱离光电接收器的敏感面,以达到测量光束偏摆修正的目的[8],并将试验结果的偏差降到最小,从而提高测量准确度,保证试验的准确性和稳定性。

本文采用LS-DYNA软件对光栅表面粘贴处的应力应变分布进行性能分析[6],确定出该表面变形微位移量与测量光束偏摆角度的关系,通过对入射镜组的合理选型与设计,达到对测量光束修正的目的,不仅提高了系统的测量精度,而且还可以满足强冲击的测量需求[7]。

1 基于LS-DYNA的仿真分析

本文的研究对象为砧体表面的光栅结构,光栅与砧体的连接方式默认采用胶接处理,但不同部分的接触方式设置又会影响到计算结果的精度与解算时间。因此下文主要从LS-DYNA的解算特点与接触处理两方面进行介绍[9]。

1.1 LS-DYNA特点

在有限元仿真计算中,针对多体动力学研究对象的振动、冲击等高速碰撞问题,一般选用LS-DYNA模块进行仿真分析。LS-DYNA的非线性动力学仿真模块可以求解二维、三维等非线性结构在高速碰撞、瞬时爆炸、高速冲击下的力学问题。特别是对于其中涉及到的大变形、大位移、大转速等情况,都可以构建相应的力学结构模型,完成对应的计算。

将n个时间步时刻划分成多个节点,平均每个节点处的加速度向量表示为[10]

式中:为外加力向量,包括在单元网格中每个节点处的值;tn为终止步骤时刻;为内力向量。其组成中分向量公式为[11]

式中:为质量矩阵;为内力向量,主要包括应力场等效节点力、沙漏阻力以及接触力。其中,应力场等效节点力可由单元节点位移和刚度矩阵相乘得到;Ω为等效结点数;Fhg为沙漏阻力,主要包括控制单元的体积、密度、瞬态移动速度等参数;Fcontact为两接触面直接存在的接触力大小。

对每个节点处的速度ˉ、位移向量ˉ进行明确表示,其计算公式为

针对速度和位移向量中涉及到的时间节点要求,对所有时间公式进行重新定义计算,则时间点公式分别为

改进后，低体温、并发症合计发生率低于改进前，改进后患者满意率与医师满意率高于改进前，差异有统计学意义（P＜0.05）。 见表 1。

对于一些非线性问题的求解,一般采用静态隐式算法,其中需要涉及到大量的矩阵运算以及反复的迭代。针对本文强冲击条件下的仿真分析,引用LS-DYNA中显示动力学模块,可以有效解决边界条件接触设置等问题。此算法的主要特点是对于复杂的矩阵不需要求逆,采用中心差分公式直接进行求解。内向量的计算可以不需要检查收敛的情况,通过设置小的时间步来保持稳定的状态。

中心差分公式是一种显示算法,其特点是稳定计算,为了准确求解强冲击条件下的砧体碰撞问题,必须要设置较小的时间步长,保证其小于一个特定的临界值,这样可以确保结果收敛,其临界时间步长要求为[13]

式中:ωmax为结构的固有频率。

求解具体问题时,时间步长必须小于该方程计算得出的某个临界值。由于显示算法具有时间步长小、计算过程方便、求解结果精度高的特点,因此LS-DYNA中的显示动力学法适用于瞬态问题的分析。

1.2 LS-DYNA中的接触处理

在高速碰撞冲击条件下,各部分相接触的材料类型、接触方式均存在差别,通常情况下采用罚函数法和约束法两种方法进行求解。两种方法的区别是在有限元分析中接触设置的特点不同,需要根据两接触面的结构尺寸参数与材料本身特性计算出具体的接触刚度大小,从而选择合适的方法。若两个接触面的材料刚度差别较小,可采用罚函数法进行处理;若两个接触面的材料刚度有较大差别,则采用约束法进行处理,即通过采用接触的节点质量和全局的时间步长计算线性接触弹簧的刚度,与材料本身的性能不发生关联。

本次的仿真对象是带有毛毡缓冲垫的砧体金属结构,端面的固定装置也采用金属材料制成,所以在子弹撞击毛毡时,毛毡与砧体尾部的接触设置采用约束法进行处理,通过将节点质量除以时间步长的平方与比例因子的乘积来确定稳定性,从而得到可靠的刚度值。通过引入罚函数因子明确罚函数的具体物理意义,完成对非线性接触刚度的处理。

2 冲击砧体的结构仿真

在高速冲击条件下,砧体上的光栅会由于外激励的影响发生偏摆,造成输出结果产生一定的误差。因此,本文通过有限元仿真软件ANSYS/LS-DYNA模块[13],模拟分析运动的砧体结构及合作目标在不同速度值下结构表面应变和应力分布趋势。由于光栅与砧体结构连接处采用镶嵌式连接,默认合作表面上的状态即为光栅的变形情况。通过对不同速度值下的模型进行计算,结合投影到各个平面上的位移尺寸,确定光栅发生偏移的距离和角度,为入射镜组的合理选型与设计提供重要参考。

2.1 几何模型

完整的冲击砧体结构由毛毡、砧体和保护盖三部分组成。尾部一侧为深度13 mm,直径26 mm的圆柱孔,其主要作用是放置不同厚度的毛毡结构,根据试验需求获得理想的脉宽参数。毛毡作为缓冲材料,采用天然动物纤维制成,其集聚粒子的效果好、单位面积集聚容量大、压力损失低并且具有较强的缓冲性能。毛毡的材料性能参数如表1所示。

表1 毛毡材料的力学性能参数Tab.1 Mechanical property parameters of felt material

砧体的侧面镶嵌光栅,光栅的粘贴层是宽度为5 mm,长度为21.5 mm的矩形凹槽结构,保证粘贴上的光栅两端不会因为强大的冲击力而造成损伤。砧体结构所采用的材料是钛合金,伸长率δ=25%,材料属性如表2所示。

表2 钛合金材料的力学性能参数Tab.2 Mechanical property parameters of titanium alloy materials

钛合金材料具有较强的韧性和强度,为了保证与实际测试的情况相符合,在冲击砧体的另一端面外加一个保护盖,保证光栅的端面不会出现磨损或者断裂。设计完成的砧体结构如图1所示。

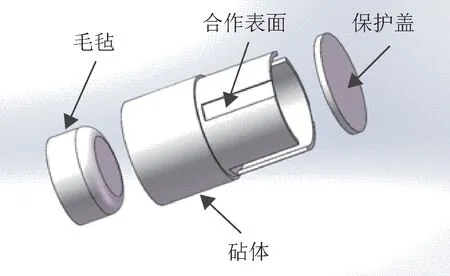
图1 结构模型Fig.1 Structure model

2.2 仿真模型计算

弹体的整体结构为圆柱形,砧体结构的前端位置尺寸较薄,在ANSYS/LS-DYNA中传统划分网格的功能比较弱,映射划分(Map)和扫琼划分(Sweep)对几何形状的要求都很高。四面体网格虽能与实际相配合,但是由四面体结构划分出的单元网格数目多余六面体,会给后期的解算造成一定的麻烦,又考虑到在计算过程中砧体的端面极易出现单元变形过大而导致的负体积,结合实际参数与测量位置需求,砧体结构采用壳单元划分网格[14],通常选择shell181为中等厚度的壳结构定义单元类型。该单元类型有四个节点,每个节点上又存在六个自由度,可以完全满足不同类型结构在X,Y,Z方向上的平动以及转动。退化的三角形选项用于网格生成的过渡单元[15-16],由于其具有非线性功能,特别适用于高速冲击仿真试验。在砧体与刚性材料冲击碰撞的仿真中,通过在端面设置一个刚性单元来模拟约束。划分网格后的模型和施加边界条件后的模型如图2和图3所示。

图2 网格划分模型Fig.2 Meshing model

图3 边界条件施加模型Fig.3 Boundary condition apply model

2.3 仿真分析计算结果

速度是影响砧体结构侵彻性能的重要因素,在高速冲击条件下,不同速度会造成砧体表面发生不同程度的变形,本文研究速度v=100 m/s时,砧体粘贴层表面变形与测量光束偏摆的对应关系,其不同时段的应变云图如图4所示。

图4 v=100 m/s时,不同时段变形云图Fig.4 Deformed cloud images in different periods wher v=100 m/s

从图中可以看出,当t=10μs时,弹体发生移动并与毛毡逐渐接触,弹体结构内部开始发生挤压变形,但由于其抗拉强度较高,足以抵抗冲击造成的影响。在t=30μs时,砧体侧壁有轻微变形,由于速度沿着弹体一直传递到砧体表面上,受到距离的限制,所以砧体变形量略小。当t=50μs时,砧体的变形开始从侧壁的两端向粘贴层位置扩散,砧体的整体结构出现挤压现象。因为边缘处的应力集中较大,接触面积小,应力会沿着所受抗力较小之处发生流动,所以变形量相对于粘贴层位置大很多。在t=70μs时,随着速度和冲击能量达到最大值,砧体结构的变形也较为明显,主要以挤压为主。砧体选用的材料是钛合金,强度较高、韧性较强,侧壁有向外扩张的趋势。粘贴层位置处的变形对测量光束偏摆影响最大,因此采用数值提取法,获取粘贴层处在X方向上的最大变形值为0.398 mm,Y轴与Z轴方向上的最大变形如图5所示,分别为0.004 mm和0.081 mm。

图5 Y轴与Z轴方向的变形云图Fig.5 Deformed cloud in Y-axis and Z-axis directions

3 光路偏摆修正

砧体与光栅的连接处发生不同方向的微位移量,导致光束测量产生相应的偏差。为了达到对光束测量修正的目的,需要借助光栅的衍射原理进行分析计算,光栅衍射满足公式[19]

式中:d为光栅常数;θ为衍射角;λ为入射光波波长,μs。

拟研制的激光测速仪的光路结构通过设计和计算,需要保证其入射光的+1级和-1级衍射光的衍射角θ垂直于光栅面。若砧体表面上的光栅发生偏摆,设偏摆角为α,则干涉光束将产生2α角度的偏转,如图6所示。偏摆角度的大小可以根据在光栅表面处投影的位移量计算得出。偏摆角度较大时,会导致干涉信号超出反射镜范围,引起信号中断,从而影响测量结果[17]。

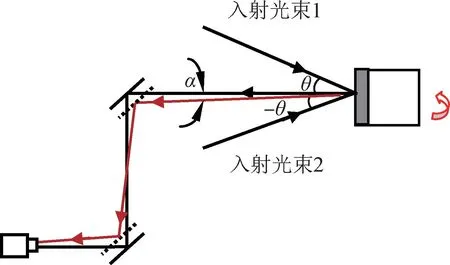
图6 光栅发生偏摆时对干涉光束角度影响示意图Fig.6 Schematic diagram of the influence of the angle of the interference beam when the grating is deflected

3.1 光路偏摆坐标搭建

为了确定测量面偏摆与平移时的具体情况,将与反射表面垂直,朝向镜组方向设为X轴正向,待测振动位移方向设为Z轴,同在反射面且与振动位移垂直的方向设为Y轴,等轴光线坐标系如图7所示。

考虑三个轴方向上的位移情况:沿Z轴、Y轴的运动分别为待测振动的方向和光栅纵向延伸的方向,对回光偏移均无影响。沿X轴的运动可以分为两种情况:一种是Z轴方向上的振动微动,位移不超过5 mm,这种近距离微动仍然处于平凸透镜的前焦面附近,后面的平行光束的角度波动在2 mrad(0.1146°)之内,也不会超出后续镜组的直径范围;另一种是Z轴的放置距离受实际情况限制,会产生十几毫米至几十毫米的偏差。距离偏大时,最大可接收偏角逐渐减小,且强度逐渐减弱,例如当远离10 mm时,在一定偏摆角度范围内,仍可接收到光,但光束已经开始不完整;当远离25 mm时,受限于平凸透镜与最后的第二级双凸镜的直径,可接收偏角变小,且光强度、质量大幅下降。距离偏小时,容许范围相对较大,最大可接收角减小得很少,光仍可进入镜组,但在不调整接收面距离的情况下,光线会过度偏折离开接收器,例如靠近10 mm时,5.5°仍可接收,接收光斑直径稍有扩大;靠近30 mm时,接收光斑直径扩大一倍,可容许接收偏摆角下降至3°。总的来说,若偏摆角较小,则距离控制十分宽松,若随机偏摆角较大,则距离控制就需要提升精度[19]。

考虑三个轴方向上的旋转情况:当围绕Z轴或Y轴旋转时,会造成偏摆角度的旋转,假设Z轴方向与出射光线确定的平面平行,则Y轴的容许角度会比Z轴稍大,原因是由于出射光口径的大小和装配结构损失带来的影响。又由于都采用的是圆反射镜,围绕以Z-Y平面上的方向为轴的在最大容许角内的偏摆都可以投射至接收面。围绕X轴的旋转,几乎没有影响,不会带来偏转,在接收面上记录的强度分布方向有所旋转,不影响测量。

3.2 光路镜组补偿设计

光束偏摆的基本路径是:从测量反射表面的偏摆衍射光先经过平凸透镜后减小了斜射程度,再经过近似于平行的斜向45°的圆平面反射镜反射到第二平面反射镜,待光线近似平行出射后进入旁路接收光路镜组,最后经过两级缩束减角透镜组投射在接收面上,偏摆镜组光路补偿路径示意图[18]如图8所示。

图8 光路补偿路径Fig.8 Optical path compensation path

各个极值路径的位移偏移量与光电元器件的参数具体如下:从待测表面射出的光,在无偏摆的情况下是直径为3 mm垂直入射的平行光束,若有偏摆,则为带有径向偏摆角度的3 mm斜入射平行光束。一般情况下,此偏摆角为小角度,最大不超过10°,由于最前方的平凸透镜的镜头口径为76.2 mm无法更改,且必须距离待测表面300 mm左右,则根据试验环境需求,可确定最大可接收偏摆角为7.2°,但受限于装配误差,且从平凸透镜出射的测量光束的口径减少了可利用的直径,结合上述动力学的仿真计算结果,通过提取投影在Y-Z平面上的变形倾斜量(即Y轴和Z轴方向上的位移量),并结合反正切函数的计算方法,可以计算出单侧偏摆角度α=arctan(0.004/0.081)=3.1°。实际会产生2α角度的偏转,则实际最大可接收偏摆角为6.2°,即超出此角度的光已经无法射入镜组中。为保证后续光线质量,遵循入射光的+1级和-1级偏摆衍射光的基本原理,建议将偏转角控制在±5.2°之间。

确定了偏转角的合理范围后,需要对镜组进行选型与设计。由入射光于是从透镜前焦面射入的,平凸透镜后的光近似为平行光,根据这束光的直径可以确定平面反射镜的直径为92.2 mm,两个反射镜只是起转向作用,直径相同。第二反射镜之后就是两级缩束镜组。第一级缩束镜组设计缩束倍数为2倍,为与转向后的光束口径匹配,第一个透镜也使用76.2 mm,焦距为300 mm的平凸透镜,第二个透镜为直径40 mm,焦距为150 mm的双凹透镜,此时的最大偏角的光束口径被缩减为30 mm左右。第二级缩束镜组设计缩束倍数为8倍,为与第一级光束口径匹配,同时减少前向的累积球差,第一个透镜使用直径40 mm,焦距为120 mm的双胶合透镜,第二个透镜为直径10 mm,焦距为15 mm的双凹透镜,此时的最大偏角以内的光束口径被缩减到小于4 mm的范围内,单角度光束的口径为3.5 mm左右,便于投射到接收器上。两级用来压缩光线偏角的镜组综合压缩倍数为16倍。最后透镜与接收面的距离可以根据实际的要求微调,但最终的偏摆角度控制在±5.2°之间,符合实测要求[20]。

4 总结

针对高速冲击情况下,光栅偏摆造成测量结果不准确的问题,利用动力学仿真,发现在v=100 m/s的情况下,粘贴位置的两侧变形最大,并呈现出由外向黏贴层内的扩展趋势,特别是在切线方向上变形较大。建议后期光栅结构在布置设计方面应确保砧体的固定端长度略大于光栅的切向长度。

入射镜组选型设计方面,为了保证入射光的强度达到最大,测量精度达到最高,偏摆角最大范围不超过±10°。结合动力学仿真位移偏移量的结果,计算出了投影在Y-Z平面上的单侧偏摆角为3.1°,双侧偏摆角为6.2°,按照遵循偏摆衍射光的基本原理,确定出最后的偏摆角为5.2°,通过选择合理的镜组类型,保证了入射光可以始终入射至探测器敏感部,最大程度上提高了激光的测量精度。