融入混沌的非均匀海洋捕食者算法

李守玉 何 庆＊

（贵州大学 大数据与信息工程学院 贵州贵阳 550025）

海洋捕食者算法(Marine Predators Algorithm, MPA)[1]是由Faramarzi等人于2020年提出的群智能算法。尽管MPA提出的时间短，但其与被囊群算法(Tunicate Swarm Algorithm, TSA)[2]，平衡优化算法(Equilibrium Optimizer, EO)[3]具有一定的可比性。

MPA将海洋中捕食者的觅食行为通过数学建模为一个优化过程，达到寻找最优食物源目的，其原理简单、参数少、易于实现，但也存在寻优精度低，收敛速度慢以及易陷入局部最优等问题。因此，为了进一步提高优化精度和加快算法收敛，本文提出融入混沌的非均匀海洋捕食者算法。

海洋捕食者算法

初始化

MPA利用随机方式初始化种群：

优化过程

MPA的优化过程是根据不同的速度比和生命周期进行划分为以下三个阶段：

位置更新

融入混沌的非均匀海洋捕食者算法(MPA-CN)

混沌初始化

群智能算法中常被用来初始化种群的方法包含混沌映射法、佳点集法、量子位Bloch球面初始化等。混沌映射具有遍历性、随机性和规律性等特点，常用来初始种群位置的混沌映射有Logistic映射和Tent映射，然而前者存在搜索盲区大，后者没有搜索盲区但存在不稳定周期导致陷入Tent映射的不动点。因此，本文采用Tent映射并对其改进，降低不稳定周期影响，使初始化个体更好的覆盖搜索空间，为算法寻优打下坚实基础。新的Tent映射的数学描述如下：

非均匀的优化过程

在优化过程中的第一阶段和第二阶段中捕食者移动速度慢于且等于猎物的情况，捕食者捕到猎物几率相对较低，从而影响算法的全局搜索能力，导致算法寻优精度不高。因此，为了进一步增强捕食者捕获猎物的成功率，本文提出非均匀的优化过程，主要让算法依据优化进行的阶段，采用随机非均匀算子调整捕食者与猎物之间的移动频率，进而增强算法的全局搜索和局部搜索能力，提高算法优化精度。非均匀算子(NUF)的数学描述如下：

实验结果分析与讨论

为了测试MPA-CN的鲁棒性和有效性，通过6个具有不同特征的基准测试函数，如表1示。同时，将MPA-CN与EO、TSA、MPA进行公平对比，种群大小为25，最大迭代次数为500，独立运行30次，实验结果记录在表2中。

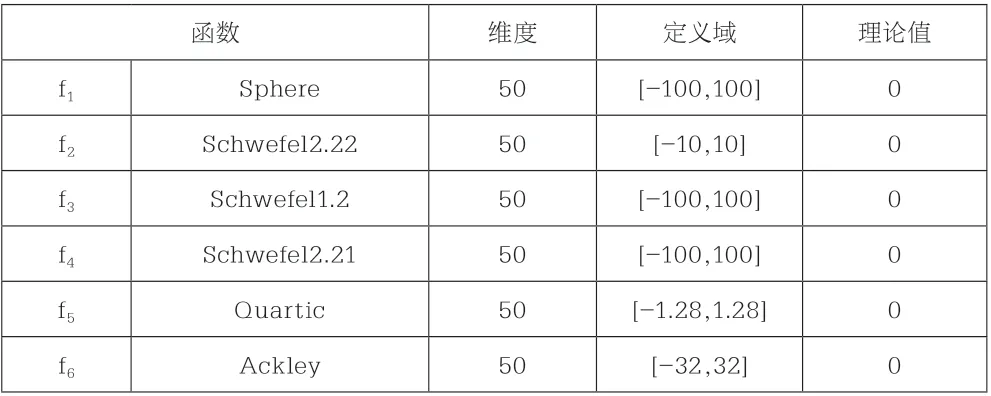
表1 基准测试函数

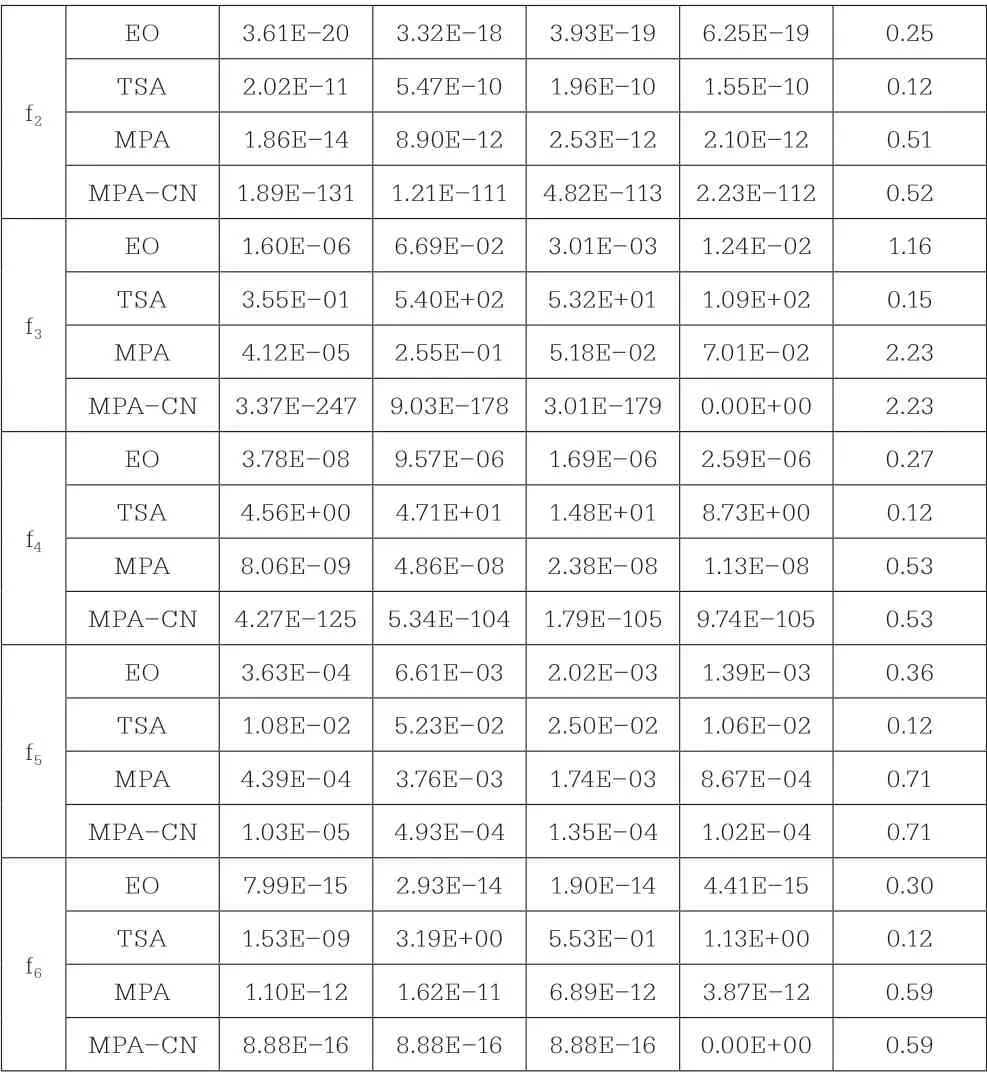
EO 3.61E-20 3.32E-18 3.93E-19 6.25E-19 0.25 TSA 2.02E-11 5.47E-10 1.96E-10 1.55E-10 0.12 MPA 1.86E-14 8.90E-12 2.53E-12 2.10E-12 0.51 MPA-CN 1.89E-131 1.21E-111 4.82E-113 2.23E-112 0.52 f2 EO 1.60E-06 6.69E-02 3.01E-03 1.24E-02 1.16 TSA 3.55E-01 5.40E+02 5.32E+01 1.09E+02 0.15 MPA 4.12E-05 2.55E-01 5.18E-02 7.01E-02 2.23 MPA-CN 3.37E-247 9.03E-178 3.01E-179 0.00E+00 2.23 f3 EO 3.78E-08 9.57E-06 1.69E-06 2.59E-06 0.27 TSA 4.56E+00 4.71E+01 1.48E+01 8.73E+00 0.12 MPA 8.06E-09 4.86E-08 2.38E-08 1.13E-08 0.53 MPA-CN 4.27E-125 5.34E-104 1.79E-105 9.74E-105 0.53 f4 EO 3.63E-04 6.61E-03 2.02E-03 1.39E-03 0.36 TSA 1.08E-02 5.23E-02 2.50E-02 1.06E-02 0.12 MPA 4.39E-04 3.76E-03 1.74E-03 8.67E-04 0.71 MPA-CN 1.03E-05 4.93E-04 1.35E-04 1.02E-04 0.71 f5 EO 7.99E-15 2.93E-14 1.90E-14 4.41E-15 0.30 TSA 1.53E-09 3.19E+00 5.53E-01 1.13E+00 0.12 MPA 1.10E-12 1.62E-11 6.89E-12 3.87E-12 0.59 MPA-CN 8.88E-16 8.88E-16 8.88E-16 0.00E+00 0.59 f6

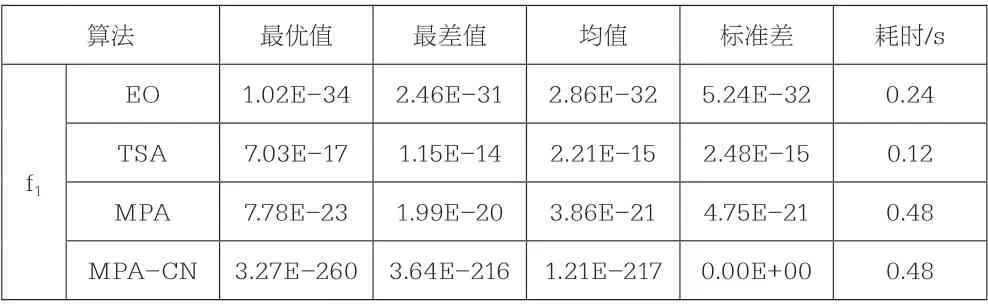
表2 实验对比结果

另外，本文的实验环境为Windows7，64位操作系统，CPU为Inter Core i5-6500H，主频3.2GHz，内存8GB，算法基于MATLAB2014b，使用M语言编写。

由表2的实验对比结果可知，MPA-CN对f1～f9函数进行求解时，MPA-CN的五个性能指标均获得最高的优化精度。从与MPA相比的角度看，MPA-CN通过新Tent映射初始化种群位置，使得种群在寻优开始阶段分布更加均布，有助于算法的后续寻优；利用非均匀优化提高捕食者的成功，增强算法的全局搜索和局部搜索能力，可以进一步的提高算法的优化精度。

从与其他先进的群智能算法相比的角度看，对f1～f4求解时，其他先进算法得到优化精度都远都离理论值，这说明其他群智能算法存在先陷入局部最优和收敛速度慢的问题，而这些问题在MPA也有体现；在求解f5～f6函数时，虽然所有求解的算法获得优化精度接近，但MPA-CN仍能获得最高的优化精度，这说明改进Tent映射和非均匀优化有效结合可以提高MPA的竞争力。

为了克服MPA存在寻优精度低和收敛速度慢的问题，提出融合混沌的非均匀海洋捕食者算法。混沌机制对种群进行初始化，使得初始种群分布更加均匀，帮助提高算法的优化精度。另外，非均匀优化增强全局搜索与局部搜索的能力，进而提高优化过程中捕食者的捕食成功率。文中使用经典测试函数并用五个性能指标对MPA-CN的性能。实验结果表明MPA-CN具有更高的寻优能力和出色的竞争力。在未来的研究中，考虑将算法应用到工程实践上，以进一步验证算法的性能。