《章末知识建构——小专题：手拉手模型》教学设计

李福芹

一、教学目标

（一）知识与技能

1、了解手拉手模型的基本构图

2、掌握手拉手模型的全等与七大结论

3、会利用手拉手模型解决实际问题

（二）过程与方法

在探讨过程中让学生体会从特殊到一般和类比的数学思想方法

（三）情感态度与价值观

在小组合作交流，探讨解决问题的过程中培养学生的集体荣誉感，提高学生的几何思维。

二、教学重难点

1、教学重点

能熟练的找出手拉手模型中的全等三角形及其七个结论，并能自己证明。

2、教学难点

会利用手拉手模型的基本结论，解决实际问题。

3、教学方法

教师讲练和启发引导，学生自主探究合作交流。

三、教学过程

1.手拉手模型的基本构图

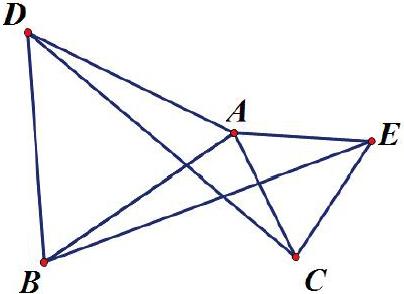
教师：展示教材原题

如图，△ABD，△AEC都是等边三角形。求证：BE=CD

学生答：分组合作交流，上台展示成果。

2.题目变式

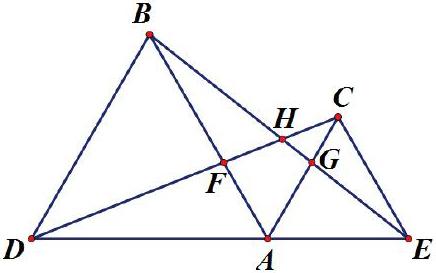
变式一：如图，A、D、E三点共线，△ABD，△AEC都是等边三角形。 探索结论：

教师引导学生，利用平时积累的数学经验，得出有关模型的几个结论。

学生：分组合作交流，得出几个结论。

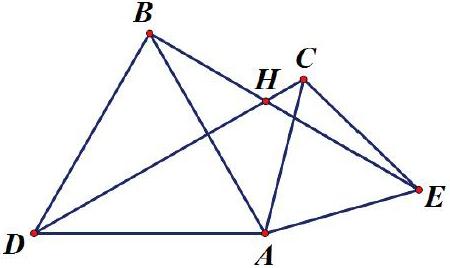
变式二：如图，当A、D、E三点不共线时， △ABD，△AEC仍是等边三角形。上题的七个结论还成立吗？

教师引导学生，利用平时积累的数学经验，得出有关模型的几个结论。

学生：分组合作交流，得出几个结论。

变式三：若△ABD，△AEC是等腰直角三角形，结论还成立吗？

教师引导学生，利用平时积累的数学经验，得出有关模型的几个结论。

学生：分组合作交流，得出几个结论。

变式四：若△ABD，△AEC为等腰三角形，且∠BAD=∠CAE=α，结论还成立吗？

教师引导学生，利用平时积累的数学经验，得出有关模型的几个结论。

学生：分组合作交流，得出几个结论。

设计意图：通过教材母题的变式，让学生熟悉模型，并且得到几个相关结论。 3. 总结提升

（1）手拉手模型的定义

（2）手拉手模型的三角形全等证明 （3）手拉手的七个结论证明

教师引导，学生展示。

4.学以致用

在平面直角坐标系中，△AOP为等边三角形，A（0，1），点B为y轴上一动点，以BP为作等边△PBC，CA的延长线交x轴于点E。 （1）求证：OB=AC. （2）求∠CAP的度数.

（3）当点B运动时，AE的长度是否发生改变？

5.课堂小结：

教师：本节课同学们有什么收获？ 同学：独立思考，合作交流，总结提升 教师：总结模型，提炼数学思想方法

四、课后反思

1. 对数学模型的反思--学会对模型的整理和反思

对于学生来说，学习数学的一个重要目的是要学会数学模型的整理与思考，用数学的眼光去看世界。而对于我们来说，要从“教”的角度去看数学，我们不仅要能“做”，还应当能够教會别人去“做”所以小专题就可以很好地将课进行整合。

2.对学数学的反思

当学生走进数学课堂时，他们的头脑并不是一张白纸--对数学有着自己的认识和感受。我们不能把他们看着“空的容器”，按照自己的意思往这些“空的容器”里“灌输数学”这样常常会进入误区，因为师生之间在数学知识、数学活动经验、兴趣爱好、社会生活阅历等方面存在很大的差异，这些差异使得我们对同一个教学活动的感觉通常是不一样的。要想多“制造”一些供课后反思的数学学习素材，一个比较有效的方式就是在教学过程中尽可能多的把学生头脑中问题“挤”出来，使他们解决问题的思维过程暴露出来。

总之，本节课，师生之间很好地进行了融合，但是对也数学思想的提炼和应用还是一个漫长的过程，需要我们不断地努力。