基于等效模型的铰制孔螺栓力学设计与优化*

周夕维，陈腾飞，向华平

（南京电子技术研究所，江苏南京210039）

引 言

螺栓连接形式广泛应用于工程结构中，特别是那些需要经常装拆的部件和部位，必须使用螺栓连接。在航空电子产品结构件中，螺栓类连接件的应用则更为普遍[1]。

螺栓连接结构存在的接触和预紧力等非线性因素对有限元计算结果影响较大。国内外专家学者对螺栓连接结构进行了大量的数值模拟计算和实验研究。对螺栓连接结构进行模拟计算时，普遍采用三维实体建模法，并对螺栓模型进行细致的网格划分，以确保数值计算的准确性[2-4]。但是，对于复杂机械结构如多轴伺服转台，装配时会使用大量螺栓进行连接。螺栓数量的增加导致数值模拟计算量显著增大，计算速度明显降低。因此，有必要对螺栓模型进行合理简化，从而提高多螺栓连接模型的计算效率。

本文以某两轴伺服转台为例，通过等效刚度模型对铰制孔螺栓进行简化处理，建立系统级有限元模型，仿真得到各处螺栓的三向载荷。根据载荷大小对螺栓布局进行优化，得到布局最优解。在此工况下，按照第四强度理论，对螺栓进行强度和寿命校核，验证其工程合理性。

1 工程背景介绍

伺服转台通过基座与载机平台连接，驱动负载在规定时间周期内到达指定位置，并保证相应的指向精度。伺服转台包括基座、下壳体、电机组件、万向支架和驱动支臂，其外形见图1。

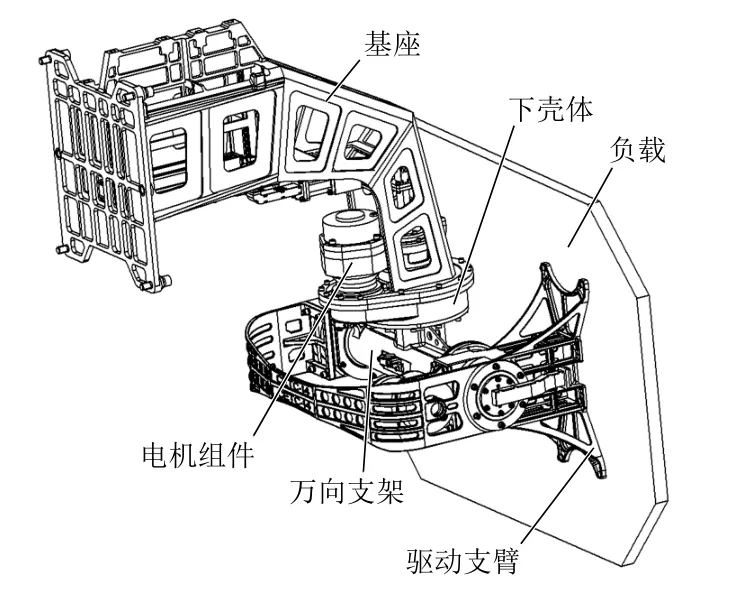
图1 伺服转台外形图

伺服转台与驱动的负载是一个串联结构，二者形成的组合载荷经由基座传递给载机平台，载机平台的振动与冲击载荷也反向通过基座传递给整个伺服转台。这样一来，基座和下壳体之间的连接就承担了系统近95%的载荷，因此其力学设计就显得尤为重要。同时为了保证良好的装配精度，基座与下壳体之间通过M6H5 的铰制孔螺栓进行连接。

基座与下壳体之间的螺栓布局按照连接件刚度匹配原则进行设计，如图2 所示。对于刚度连续的区域，螺栓对称密排布；对于刚度不连续的区域，螺栓仅仅起到辅助安装功能，采用稀疏排列策略[5]。

图2 基座与下壳体连接螺栓布局

2 有限元力学仿真

2.1 螺栓等效刚度计算

螺栓选择HB 1-103 型，材料为30CrMnSiA。螺栓连接的基座与下壳体的材料均为2A12（H112）铝合金，弹性模量E1[6]相同。

对于螺栓的轴向刚度，可以认为在任意垂直于螺栓轴线的截面上的压应力为均匀分布，将螺栓简化为空心圆柱体，螺栓的轴向刚度可以表示为：

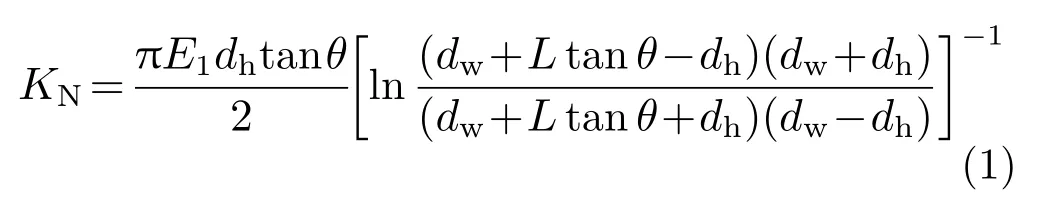
式中：dh为螺栓孔直径；dw为垫片直径；L 为连接处基座厚度ts加连接处下壳体厚度tx，即L=ts+tx；θ 为基座和下壳体连接部位压应力分布的半顶角。

对于螺栓的剪切刚度，基座和壳体之间的连接形式可以认定为搭接形式。螺栓的强度设计将螺栓的承载限定在弹性段内，基于此，螺栓的剪切柔度C 可以表示为：

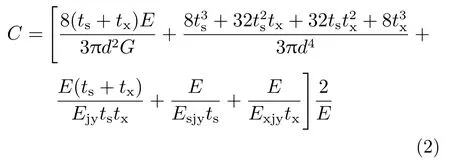
式中：d 为螺栓直径，由于是铰制孔，d = dh；E 为螺栓的弹性模量；G 为螺栓的剪切模量；Ejy为螺栓的挤压模量；Esjy为基座的挤压模量；Exjy为下壳体的挤压模量[7]。

螺栓的剪切刚度Kτ为柔度C 的倒数，表示为：

提取模型中基座的厚度ts= 8，下壳体的厚度tx= 10，带入基座、下壳体及螺栓的材料参数，得到螺栓简化模型的等效刚度为：

KN=140 000 N·m, Kτ=4 800 N·m

2.2 有限元模型建立

基座与下壳体之间的连接螺栓采用钉元进行模拟，每个钉元使用3 个一维弹簧元进行建模，弹簧的刚度来自螺栓简化模型的等效刚度。在基座与下壳体配合面的螺栓铰制孔中心各建立1 个独立节点，以独立节点为主节点分别与对应孔壁上所有的节点创建多点约束，约束3 个方向的平动自由度。然后在这两个独立节点之间建立弹簧单元，模拟螺栓的轴向拉压刚度和面内剪切刚度[8]。基座与下壳体连接螺栓简化情况如图3 所示，图中数字为螺栓编号。

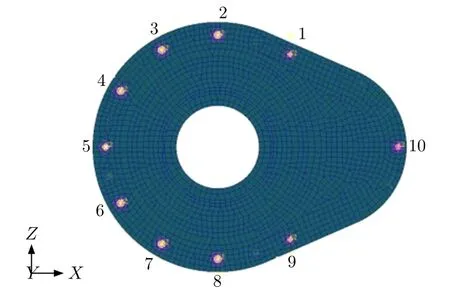
图3 基座与下壳体连接螺栓简化模型

按照上述原理及流程对伺服转台的其他连接进行同样处理，最终得到系统的仿真模型，如图4 所示。

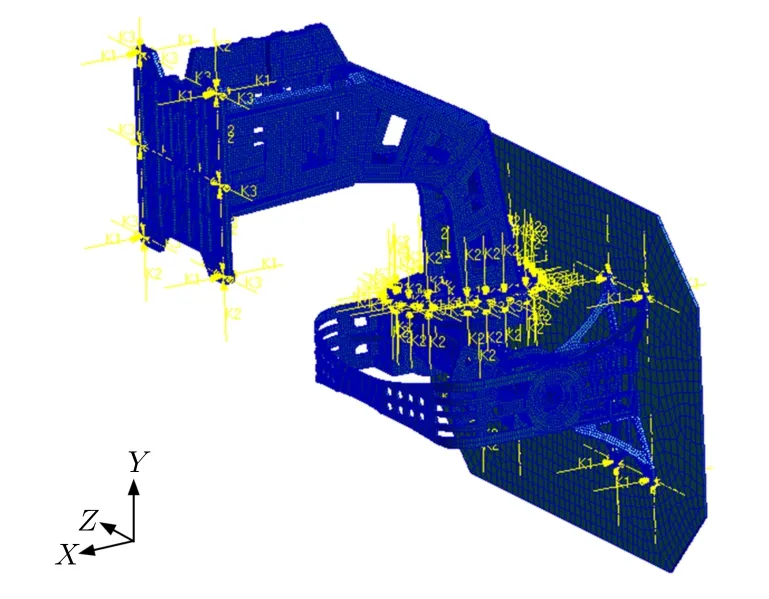
图4 伺服整体有限元仿真模型

2.3 螺栓应力提取

伺服转台工作时需要承受3 轴向后峰锯齿波冲击载荷，峰值加速度为20g，脉冲宽度为11 ms。

按照图4 坐标系定义，选取最为恶劣的Y 向冲击对伺服转台进行系统仿真，提取该方向下各编号螺栓的轴向拉应力与剪切应力，如图5 所示。

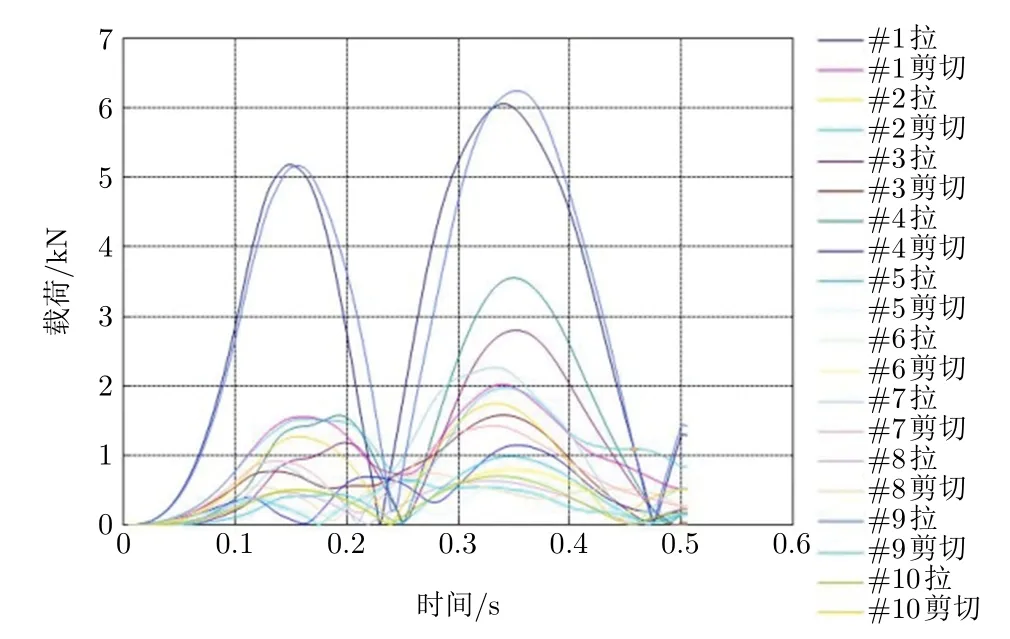
图5 各螺栓载荷曲线

由图5 可知，#1 和#9 螺栓相对于其他螺栓，应力水平偏高，这与#1 和#9 螺栓位于传力主通道边沿，存在较大的应力集中有关，因此有必要对螺栓分布进行优化。选择0.35 s 处的应力幅值开展均衡性优化。

3 螺栓布局优化

伺服转台的基座与下壳体的连接螺栓位于图6 所示的黑色中心线上。各螺栓之间的间距和为定值C，C 为本次优化的边界约束条件。另外，螺栓的间距还需满足最小扳手空间要求C1。

图6 螺栓布局边界曲线

以各螺栓的拉应力均衡性作为优化目标，通过方差函数进行数学表达。以各螺栓之间的间距作为设计变量，同时带入上述边界约束，得到本次优化的数学模型，其表达式为：

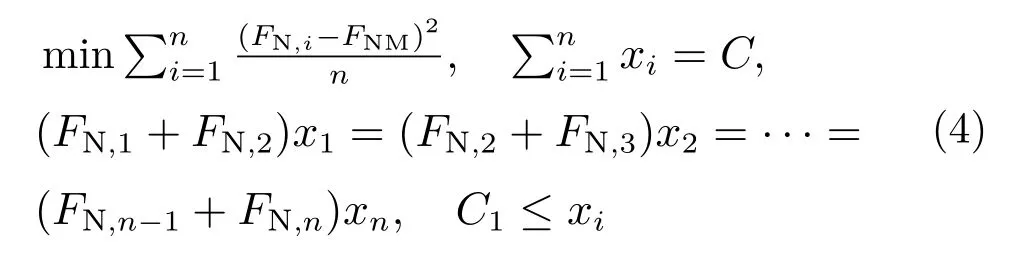
式中：n 为螺栓编号，n = 10；FN,i为编号为i 的螺栓的轴向拉应力；FNM为各螺栓轴向拉应力平均值；xi为i 号螺栓与i+1 号螺栓之间的距离[9]。

固定#10 螺栓位置，带入已知条件，获得各螺栓优化后的间距。修订螺栓孔间距参数，得到图7 所示的优化后螺栓布局。

图7 优化后螺栓布局

更新有限元模型后重新计算，得到优化后的螺栓轴向拉应力和剪切应力，如图8 所示。螺栓最大轴向载荷降低了29.5%，各螺栓的轴向拉应力幅值均衡性已经大幅提升。

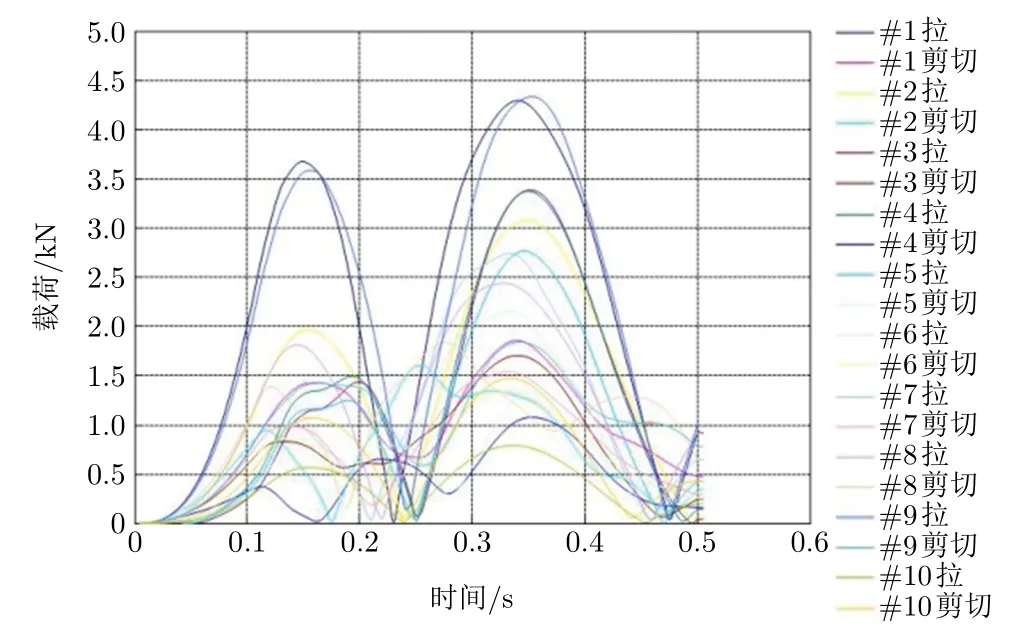
图8 优化后各螺栓载荷曲线

4 强度与寿命校核

4.1 强度校核

按照轴向拉应力与横向剪切应力核算螺栓在冲击载荷下的安全性，螺栓实际的轴向拉应力σ 和横向剪切应力τ 可以表示为：

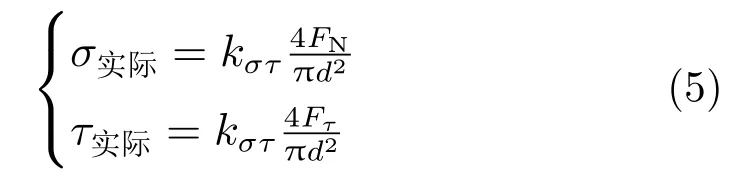
式中：kστ为仿真修正系数；FN为轴向载荷，本次核算取时间周期内的最大值；Fτ为剪切载荷，本次核算取时间周期内的最大值。

根据各螺栓载荷曲线，FN= 4 338 N，Fτ=1 862 N。取kστ=1.3，d=6 mm。带入式(5)得到：

σ实际=199.4 MPa, τ实际=85.6 MPa

螺钉材料为30CrMnSiA，材料的许用轴向拉应力[σ] = 0.7σs= 716 MPa，材料的许用剪切应力[τ] = 0.25σs= 256 MPa，σs为材料屈服强度。由于螺钉承受交变载荷，因而取许用安全系数[S] = 2.5对螺栓强度进行校核：

σ名义=[S]×σ实际=498.5 MPa ＜[σ]

τ名义=[S]×τ实际=214.0 MPa ＜[τ]

因此，优化后螺栓满足强度设计要求。

4.2 寿命校核

根据第四强度理论，螺栓组合应力可以表示为：

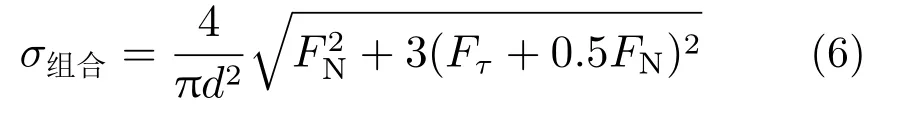
按照保守原则，FN和Fτ取4.1 节中的最大值。带入这些已知条件得到：

σ组合=290.6 MPa

根据螺栓的材料，螺栓的疲劳强度可以定义为：

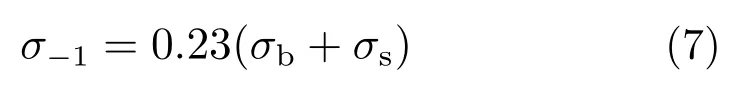
式中，σb为材料抗拉强度。带入材料数据，得到：

σ−1=529 MPa

考虑螺栓的加工因素及应力集中情况，螺栓可以承受的疲劳极限应力幅值为[10]：

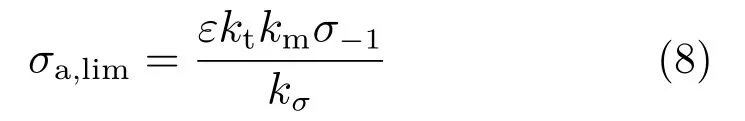
式中：ε 为尺寸系数，取1.1；kt为螺纹制造工艺系数，取1.4；km为螺纹材料系数，取1.4；kσ为螺纹应力集中系数，取1.3；取安全系数[S] = 2.5，得到螺栓的疲劳许用应力幅值为：

因此，优化后螺栓的疲劳寿命满足设计要求。

5 结束语

本文以某伺服转台为例，详细介绍了系统级产品内部螺栓的载荷获得、应力提取、布局优化、强度校核及寿命预测的设计全流程。相比传统有限元仿真，该方法具有以下突出优势：

1）相较于纯理论核算，可以有效体现螺栓的承载不均衡性，降低预测误差；

2）相较于详细模型核算，大大减少了有限元建模工作量，减少了计算资源消耗，从而大大提升了有限元仿真校核工作效率；

3）可以快速获得螺栓的优化布局，降低螺栓间承载的不均衡性，从而大大提升连接可靠性。

该方法对同类工程问题具有一定的应用价值。