基于精英保留策略遗传算法的生物电阻抗特征参数提取
徐逸帆,曹乐,黄经纬,阚秀
上海工程技术大学电子电气工程学院,上海201620
前言
生物阻抗频谱(BIS)是一种基于电路的生物组织阻抗测量和监测技术,通过分析BIS信号可以知道生物组织的生理和病理状态[1]。近年来,BIS 技术在在早期疾病诊断、生物组织液监测、生理状态评估等方面应用广泛[2-4]。2003年,Cox-Reijven[5]利用BIS技术对胃肠道疾病患者实际无脂肪质量进行评价,解决了传统方法评价困难的问题。2009年,Jaffein等[6]通过分析50 kHz下腕踝的BIS特性,对细胞外液进行水分测定,为人体成分分析奠定基础。2013年,Hornero 等[7]设计了一种用于评价肌肉及心血管活动的生物阻抗监控系统,通过对单个细胞进行BIS 分析,研究其他细胞的生理参数。2016年,何想等[8]基于所采集不同人手掌的BIS数据,通过提取特征参数对手掌所属身份进行识别。
Cole-Cole 生物电阻抗特征方程的建立,为生物阻抗参数提取和分析提供了有效理论工具,越来越多的学者关注Cole 参数提取方法。2013年,Yang[9]对经典最小二乘法(LS)和最小一乘法(LAD)的Cole参数提取效果进行实验对比,结果证明LAD 在处理受噪声扰动数据时具备更好的鲁棒性。2015年,Nejadghol 等[10]采用奇异值分解法对BIS 数据进行处理,降低了Cole 参数的提取误差和标准差,并通过手臂实验进行了证明。2016年,陈恒等[11]利用模拟退火(SA)算法和阻尼(LS)算法进行联合反演求解Cole参数,解决了经典LS 算法对于初始值依赖的问题。2018年,郭玥[12]将LAD 算法和SA 算 法 结合提取Cole参数,规避了LAD 迭代求导的问题,并对初值选择误差和易陷局部最优问题进行了分析。虽然现有方法在一定程度上解决了Cole 参数的提取问题,但是普遍存在对奇异点和随机噪声敏感度高、鲁棒性差和拟合时间长等缺点。本文采用精英保留策略和LAD 算法对传统的遗传算法(GA)进行改进,给出一种鲁棒性强、收敛速度快的Cole 参数提取新方法,并将仿真结果与现有方法进行对比,验证所得结果的实用性与有效性。
1 生物电阻抗特征参数提取
1.1 Cole-Cole模型
研究发现低频电流(低于1 MHz)只能流经细胞外液,而高频电流可以穿透细胞膜流经细胞内外液[13]。根据生物细胞组织的这种阻抗特性,通常采用如图1所示的等效电路分析生物电性质及其变化规律,Re是细胞外液电阻,Ri是细胞内液电阻,C是细胞膜电容。

图1 生物体等效电路模型Fig.1 Biological equivalent circuit model
1940~1941年,美国研究学者Cole等[14]基于生物组织等效电路提出Cole-Cole理论,即生物电阻抗实际测量值的轨迹是复平面第4象限中的一段圆弧且圆心在第1象限内(图2)。
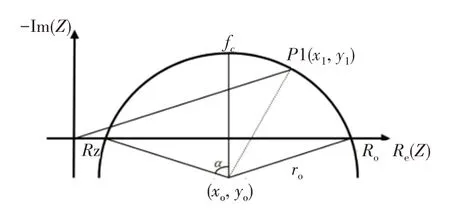
图2 生物组织Cole圆弧曲线Fig.2 Biological tissue Cole arc curve
建立如下生物电阻抗特征方程:

其中,Z(ω)为生物复阻抗,ω为角频率,R∞为频率无穷大时的电阻,R0为直流(频率为0)时的电阻,α为散射系数(0<a<1),τ为弛豫时间,τ对应特征频率fc:

1.2 生物电阻抗特征参数提取方法
为深入分析生物电阻抗性质及生物组织变化规律,需要基于测量数据求得生物电阻抗等效电路的模型参数。然而,由于受到测量仪器精度和内外界噪声等因素的影响,实际测量到的BIS数据大多分布在标准圆弧轨迹的两侧[15],这种情况下需要对采集到的BIS 数据进行拟合,求取Cole-Cole 曲线对应的圆心(x0,y0)和半径r0,再由几何关系进一步确定生物电阻抗模型的特征参数,如下所示:

从式(6)可以看出,测量误差直接导致弛豫时间τ不确定。实际中通常采用如下式表示的多数据点对应求均值的方式确定弛豫时间τ:

综合以上分析,Cole-Cole 模型特征参数提取的关键是对实测BIS 数据的有效拟合。现有的拟合结果大多通过LS、LAD 和SA 等方法得到,这些方法存在迭代过程中陷入局部最优、前期设置参数较多和人机交互依赖性强等缺点。本文提出精英保留策略遗传算法(EGA)-LAD 弥补现有拟合算法的不足,提取更为精准的Cole-Cole模型特征参数。
2 EGA
2.1 EGA概念
GA模拟了自然界中生物“优胜劣汰”的进化过程[16],利用适应度函数对种群中个体进行评价,淘汰适应度低的个体,经过随机选择、交叉和变异等遗传操作,实现生物种群的优化。但这一过程中,种群中适应度最高的个体可能会遭到破坏,这在一定程度上降低了GA全局搜索能力。本文采用精英保留策略对GA进行优化,将当前代适应度最高的个体作为精英个体保留,其余个体进行随机选择、交叉和变异等遗传操作,将精英个体插入到经过遗传操作后的个体集合形成新的种群。EGA-LAD提高了传统GA的全局收敛性和鲁棒性,该算法的步骤包括:种群初始化,设置适应度函数,选择、交叉和变异,精英保留策略。
2.1.1 种群初始化初始化种群通常以某一分布概率密度函数随机生成,为提高算法的反应速度和工作效率,本文使用经典LS[9]拟合值(x0,y0,r0)作为基础值,根据多次实验数据统计计算出合适阈值(hx,hy,hr),确定初始化种群的取值范围,在取值范围内随机生成种群。LS 提取Cole 参数的基本原理是:使得各离散点与拟合圆上对应点的径向误差的平方和达到最小,对应Cole参数拟合的LS表达式为:

其中,M为实际测量数据数目,xi为激励频率fi下所测生物电阻抗的实部,yi为激励频率fi下所测生物电阻抗的虚部,(x0,y0)为拟合圆的圆心,r0表示拟合圆的半径,ei表示径向误差即实际测量数据点在径向方向与拟合圆心之间距离。根据迭代法计算出的LS拟合Cole-Cole 圆的圆心坐标和半径(x0,y0,r0),经过多次实验统计出合适的阈值(hx,hy,hr),确定初始化种群取值范围hr,y0+hr],再利用均匀分布概率密度函数在所确定取值范围内随机生成初始化种群,具体操作如下:
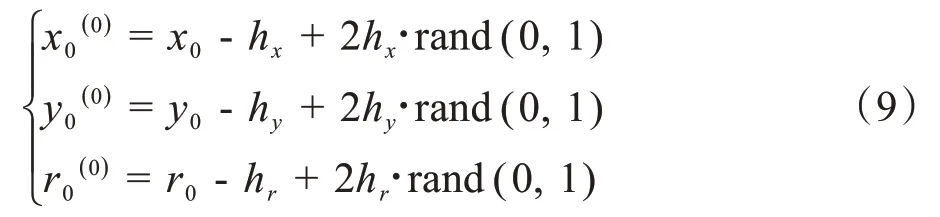
2.1.2 适应度函数在GA 中,通过适应度函数对种群中个体进行评估,选取适应度高的优秀个体遗传给下一代,适应度函数的选择直接影响算法的收敛性能和输出结果。下面引入引理1,以便理解下文中适应度函数的定义。
引理1[17]:若存在θ=θ*∈Rn,使目标函数


成立,称这n个零偏点是“0”点,反之若上式构成的方程组不成立,则Q的极小化也不成立。
定义如下适应度函数f(x0,y0,r0):
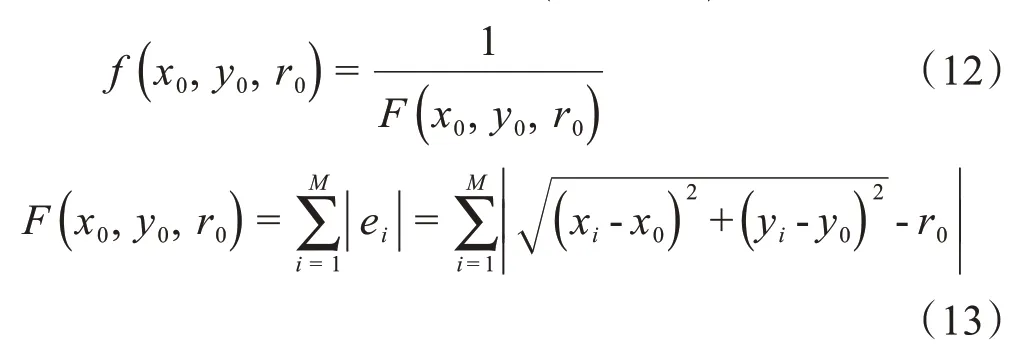
由引理1,参数(x0,y0,r0)可由最小化F(x0,y0,r0)求得。
2.1.3 选择算子本文采用锦标赛选择法对遗传基因进行选择。这种选择策略在一定程度上可以避免过早收敛和停滞现象的产生[15]。锦标赛选择法的具体策略为:从种群中随机选择k个个体(每个个体被选择的概率相同),选择适应度最好的个体作为生成下一代的父体,重复操作直到新的种群规模达到原来的种群规模。
2.1.4 交叉算子本文采用两点交叉对选出的两个个体进行交叉操作。两点交叉是指在两个配对个体基因串中随机设置两个交叉位,然后再进行交叉位之间基因块的交换。交叉发生概率记为Pc,一般Pc范围设置为0.7~0.9。对于染色体长度为l的两个配对个体x1=λ11λ12…λ1l和x2=λ21λ22…λ2l,设随机设置的两个交叉位为c1、c2,且1 ≤c1<c2≤l- 1,满足下列公式:
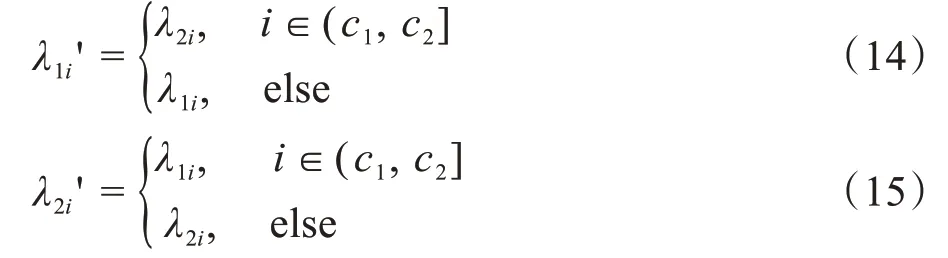
则,生成的新个体为x1' =λ11'λ12'…λ1l' 和x2' =λ21'λ22'…λ2l'。
2.1.5 变异算子生物在遗传和进化过程中会出现变异,即父代种群中某些基因按一定概率进行改变生成新的个体[18]。这里的一定概率指的是变异概率Pm,由于实际中变异的可能性非常小,一般将Pm范围设置为0.01~0.20。本文选用二进制编码符号串表示个体,利用基本位变异法对个体进行变异操作,即按照概率Pm指定变异位并将该位对应的二进制字符取反。对于个体x=λ1λ2…λl,变异运算公式如下:
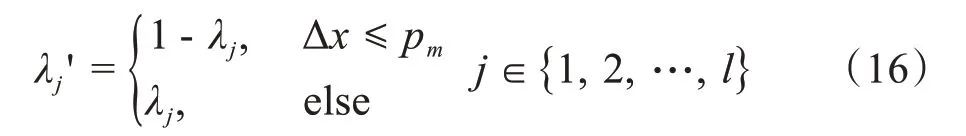
其中,Δx∈[0, 1]为任意随机数。则,变异后生成新的个体为x' =λ1'λ2'…λl'。
2.1.6 精英保留策略将每代种群进化中搜索到的最优适应度值的个体best保存为精英个体,再对剩下的N-1个个体进行遗传操作,以此避免目前种群中最好的基因受到丢失和破坏。采用EGA拟合Cole-Cole模型参数具有如下优点:(1)保留传统GA的可并行性,算法效率高,节省阻抗参数提取时间。(2)精英保留策略的引入,提高了传统GA的搜索速度,全局收敛性更快。
2.2 EGA步骤
EGA的具体步骤如图3所示。
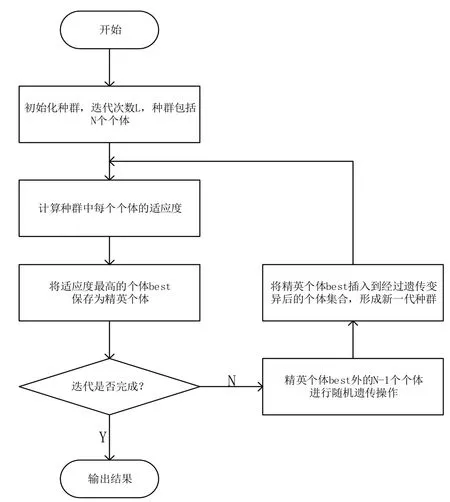
图3 精英保留算法流程图Fig.3 Elitist preservation algorithm flow chart
Step1,设置最大迭代次数L,生成包含N个个体的初始种群P(t)。
Step2,设置适应度函数,计算每一个个体的适应度,将适应度最高的个体best保存为精英个体。
Step3,判断迭代次数t是否达到L次,若满足执行Step7,否则执行Step4。
Step4,使用锦标赛法对剩下的N-1 个个体进行选择操作,重新生成规模为N-1的种群Q(t)。
Step5,对Q(t)进行交叉、变异操作,得到规模为N-1的种群Q(t)'。
Step6,将精英个体best随机插入到Q(t)'中,形成得到新一代规模为N的种群P(t)',令t=t+1,并执行Step2。
Step7,输出计算结果。
3 仿真实验方法
3.1 仿真数据集
1995年,Rigaud和Hamzaoui等[19]通过实验得到的一组肌肉阻抗特征参数R0=150 Ω,R∞=50 Ω,α=0.8,τ=3.0×10-6,从频率1 kHz~1 MHz 中选取等相角间隔的32 个频率点( )f1,f2, …,f32,32 个频率对应的即为标准BIS 数据点,且标准BIS 数据点呈均匀的对数分布,标准数据点如表1 所示。由公式(2)得到特征频率fc=53.051 6 kHz,选取的BIS数据点均匀分布在圆心为(100,-16.246 0)、半径为r0=52.573 1的Cole圆上。

表1 32个频率点对应的BIS数据点Tab.1 BIS data points corresponding to 32 frequency points
在标准BIS数据集的基础上,通过在标准数据集中添加奇异值和不同的噪声生成3组仿真数据集。
(1)存在奇异点的仿真数据集D1。
在BIS 标准数据集频率f6和f22对应的数据点处按以下公式增加30%的径向误差,其余30 个频率点的数据保持不变:

其中,Psi(xsi,ysi)表示当频率为fi时的标准数据,表示当频率为fi时的添加噪声和奇异点的仿真数据,θi表示频率fi下横轴与径向间夹角,计算公式如下:

(2)存在随机噪声的仿真数据集D2。
将标准BIS 数据中奇数频率点处数据按下式随机添加0 至±10%满足正态分布的径向误差,其余16个偶数频率点处数据保持不变:
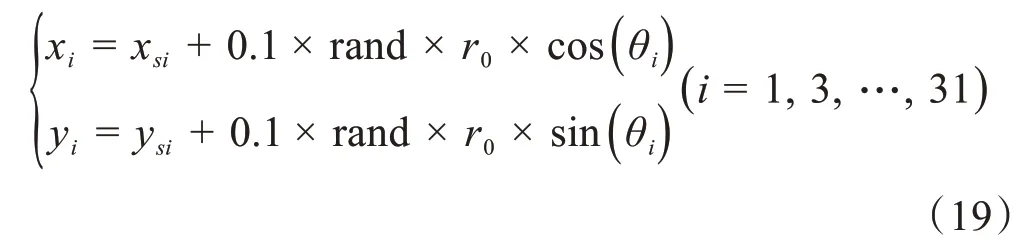
(3)奇异点和随机噪声同时存在的仿真数据集D3。
将标准数据的两个频率点f6和f22增加30%的径向误差,同时在所有的奇数频率点处数据随机添加0至±10%满足正态分布的径向误差,构成仿真数据集D3。
3.2 仿真实验结果与分析
为验证本文方法EGA-LAD 对Cole 参数提取的有效性和精确性,实验中选用经典LS、SA-LS、SALAD 和EGA-LS 4 种算法分别对D1、D2 和D3 中的BIS 数据进行拟合,并与EGA-LAD 的对应拟合结果进行比较。在实验结果中,实线代表拟合圆,虚线代表标准圆,eR0、eR∞、eα和efc分别表示Cole参数R0、R∞、α和fc的拟合误差。
3.2.1 基于数据集D1 的仿真实验结果对于仿真数据集D1,将两个偶数频率点处标准BIS 数据增加30%的径向误差。LS、SA-LS、SA-LAD 和EGA-LAD的拟合实验结果如图4 所示,表2 给出BIS 标准数据集和4种算法提取的Cole参数和拟合误差的对比值。从实验结果可以看出,LS算法的拟合效果最差,使用SA-LS 算法的拟合效果明显改善,但由于LS 算法对数据中奇异点敏感度高,使得SA-LS 算法拟合精度低于SA-LAD 算法。本文EGA-LAD 算法对Cole 圆拟合效果最好,Cole 参数提取精度最高,4 个特征参数R0、R∞、α和fc拟合误差分别为0.024 5%、0.118 6%、0.106 3%、0.036 9%。
3.2.2 基于数据集D2 的仿真实验结果对于仿真数据集D2,将标准BIS 奇数频率点处随机添加0至±10%满足正态分布的径向误差。由于添加径向误差的随机性导致每一次的拟合结果会有波动,为了更好地评价4种算法对随机噪声的鲁棒性,本文进行50 次的拟合实验,最终在表3 中分别列出50 次实验结果的平均值进行对比,LS、SA-LS、SA-LAD 和EGA-LAD的拟合实验结果如图5所示。从实验结果可以看出,LS算法的拟合效果最差,本文EGA-LAD 算法比两种改进的SA-LS 和SA-LAD 算法拟合效果好,Cole 参数提取精度最高,4 个特征参数R0、R∞、α和fc拟合误差分别为0.000 7%、0.001 8%、0、0,其中拟合的α和fc参数与标准值一致,拟合曲线与标准曲线基本重合,实验结果说明EGA-LAD 对随机噪声的鲁棒性最好。

图4 数据集D1实验结果Fig.4 Data set D1 experiment results
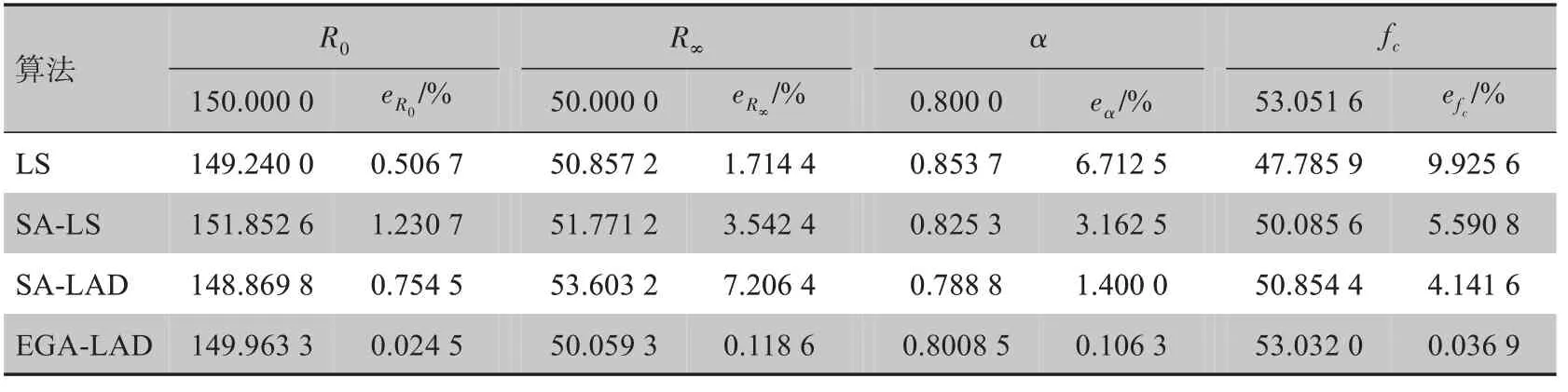
表2 D1数据集下实验结果对比Tab.2 Comparison of experimental results on D1 data set

表3 D2数据集下实验结果对比Tab.3 Comparison of experimental results on D2 data set
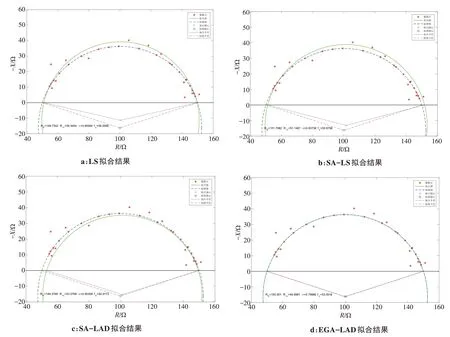
图5 数据集D2实验结果Fig.5 Data set D2 experiment results
3.2.3 基于数据集D3的仿真实验结果对于仿真数据集D3,将两个偶数频率点处标准BIS数据增加30%的径向误差,并将奇数频率点处随机添加0至±10%满足正态分布的径向误差。同样进行50次的拟合实验,最终在表4中分别列出50次实验结果的平均值进行对比,LS、SA-LS、SA-LAD和EGA-LAD的拟合实验结果如图6所示。从实验结果可以看出,相比于与仿真数据集D2的拟合结果,4种算法的拟合精度均有下降,说明奇异点对拟合结果的影响很大,本文EGA-LAD算法对Cole圆拟合效果依然最好,4个特征参数R0、R∞、α和fc拟合误差分别为0.001 6%、0.002 2%、0、0.002 1%,但在数据点出现大量偏差时EGA-LAD算法的鲁棒性会降低。

表4 D3数据集下实验结果对比Tab.4 Comparison of experimental results on D3 data set
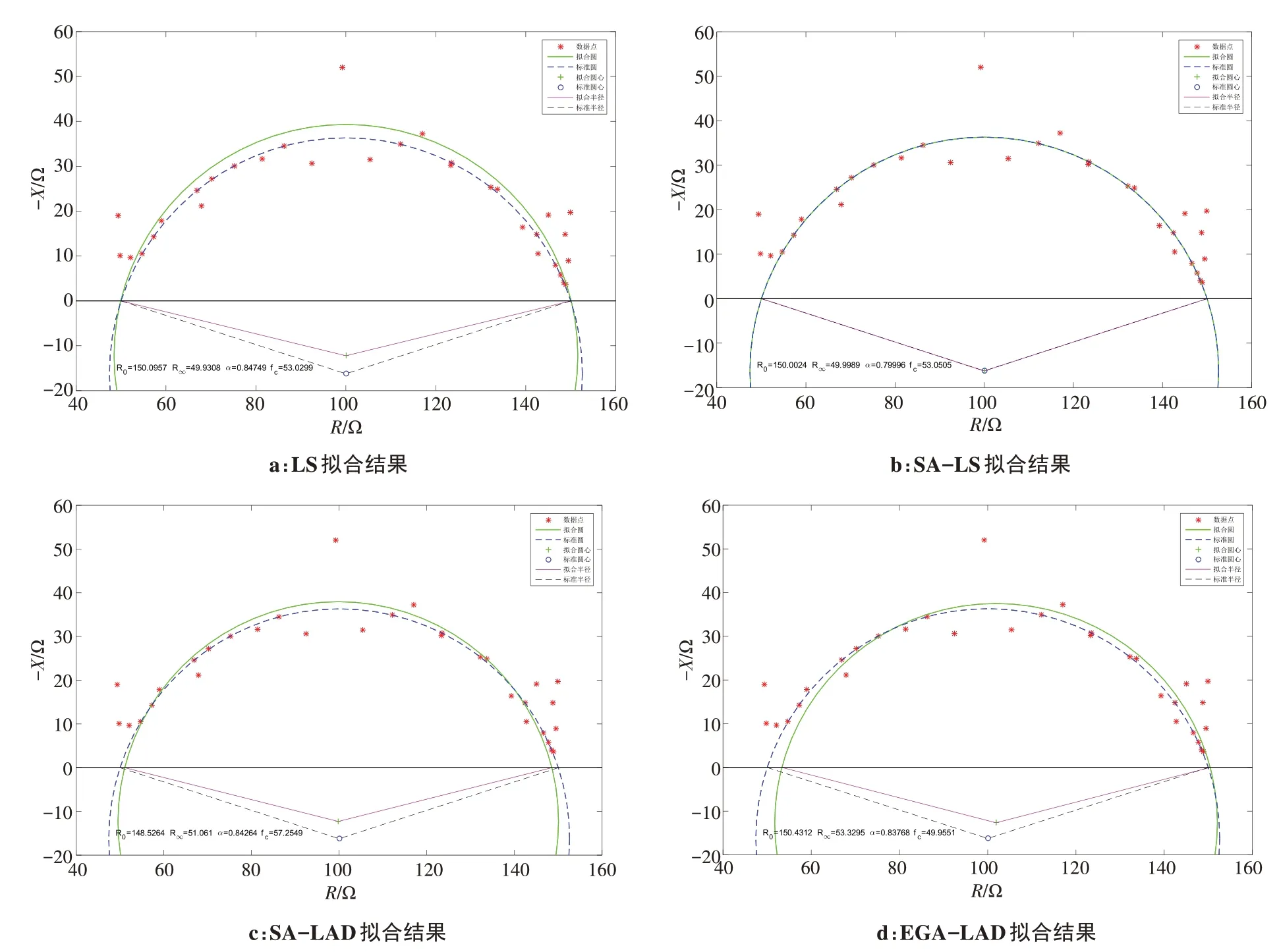
图6 数据集D3实验结果Fig.6 Data set D3 experiment results
3.3 仿真结果分析
表5 给出4种算法对于3组数据集的平均拟合时间。综合对应仿真实验结论,可知作为经典拟合方法的LS 算法用时最短速度最快,但由于其对奇异点的敏感度较高,在奇异点存在的条件下拟合精度会受到严重影响,而在BIS 应用中,对提取参数的精度要求优先于时间复杂度要求。改进的SA 改善了鲁棒性差的问题,但由于其在每一温度下均需充分搜索最优解,使得拟合时间变长,并在一定程度上影响拟合精度。本文EGA-LAD 算法具有隐式并行性,在保证拟合精度的情况下,缩短了拟合时间,提高了计算效率。

表5 不同算法拟合平均仿真时间Tab.5 Average simulation time of different fitting algorithms
4 结论
本文综合考虑精英保留策略和LAD,改进传统的GA 算法,在生物电阻抗Cole-Cole 特征模型基础上给出Cole 参数提取的新方法。通过添加奇异点和随机噪声,在标准BIS 数据集的基础上生成3 组仿真实验数据集,利用LS、SA-LS、SA-LAD 和EGA-LAD 4 种算法分别对3 组仿真数据集进行仿真拟合,比较了4 种算法的拟合精度和时间复杂度。实验结果表明,本文EGA-LAD 算法具有拟合效果好、对奇异点和随机噪声的鲁棒性强、Cole 参数提取精度高的优点,验证了EGA-LAD 算法对生物电阻抗Cole参数提取的有效性和实用性。

