复合连杆机构输出运动与动力学分析*

陆鹏飞，胡昌军

（宿迁学院机电工程学院，江苏 宿迁 223800）

随着科学技术的进步，机械设备的小型化以及机械产品的微型化对机械零件的加工方法提出了更高的要求，各种机构在这些设备中起到了关键作用。为了获得更好加工性能，对构成这些设备的机构进行运动学和动力学分析，是设计过程中极其重要的环节。 近年来，不少学者对机器人中用到的机构进行了运动及动力学分析[1-4]，这些工作提升了机器人在工业中的应用范围和性能。 Dongkyu Lee 等人[5]、王军等人[6]、Saurav Agarwal 等人[7]分别从路径生成、参数化设计以及二阶结构误差等不同方面讨论了机构设计的方法，这些方法对于机构在新型设备中的应用设计具有很好的借鉴价值。文献[8-16]从机构的运动学建模、优化分析、控制学、神经网络等角度分析研究了机构在不同设备领域的应用，有一定的价值，但都或多或少存在不同程度的不足，比如其中有些模型过于复杂，不利于应用推广等。基于此，本文分析了一种基于平面六杆机构的复合机构输出运动和动力，讨论了该机构的输出行程，建立了两种不同情况时输出行程的计算模型。

1 六杆机构的基本架构设计

笔者所设计六杆机构的运动简图如图1 所示，该机构相当于由铰链四杆机构ABCE 和一个单移副四杆机构组成，动力由曲柄 AB 输入，经过中间杆件 BC、CE、CD 将运动和动力输出，输出构件D 在杆件CD 的驱动下产生运动实现对工件的挤压成形。

图1 六杆机构的运动简图

2 六杆机构中输出构件的输出行程

如图1 所示，AB、BC、CE 与机架组成的铰链四杆机构为双曲柄机构时，CE 杆与CD 杆位于同一条直线且C 点在E 点下方，输出构件D 处于最低端D1，而 CE 杆与CD杆位于同一条直线且C 点在E 点上方，输出构件D 处于最顶端D2，D1D2的距离即这种情况下输出构件D 的最大输出位移，大小为：

AB、BC、CE 与机架组成的铰链四杆机构为曲柄摇杆机构时，CE 不能绕机架转整周，AB、BC 处于一条直线时为 D 点的可能最顶端，如图 2（a）（b）所示，很明显，图 2（a）应该是D 点处于最顶端的机构位置。

图2 D 点可能最顶端的六杆机构位置简图

在图 2（a）的⊿ACE 中：

由图2 很容易得到：

D 点处于最底端时：

输出构件D 的输出位移D1D2可通过联立式 （2）～式（5）得到的方程组解得结果。

3 六杆机构的输出力分析

该机构中BC 杆和CD 杆均为二力杆，因此，C 点的受力情况如图1 所示，杆BC 和杆CD 在C 点的作用力分别为F和Q，以杆CE 为研究对象，F 和Q 对E 点的合力矩为0 得：

以输出构件D 为研究对象得：

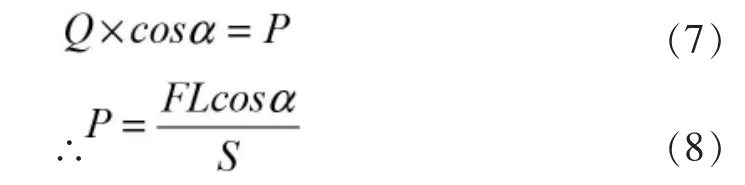
从式（8）可以看出，输出构件 D 的输出力与 S、L、α 相关，要想获得所需的挤压力可以通过改变这些参数的大小来实现。

4 六杆机构的运动及动力学仿真

4.1 机构仿真模型的建立

取图1 各杆件的长度分别为AB=50mm、AE=235mm、BC=255mm、CE=120mm、CD=135mm、β = 60°，将这些数据分别代入式（2）～式（5），并进行求解，结果为：

打开ADAMS 软件，依据上述各杆件的长度以及运动副的位置创建MARK 点，再创建组成机构的各杆件，为各杆件之间以及部分杆件与地面之间创建约束，则为图1 所示压力机主传动机构创建的仿真模型如图3 所示。

图3 六杆动机构的仿真模型

4.2 机构仿真分析

在AB 杆上施加驱动，设置仿真时间为55，仿真步数为100，对机构进行仿真。 得到输出构件D 的位移曲线如图4 所示。

对图4 的位移曲线进行测量所得结果如表1 所示。

表1 测量位移曲线所得结果

由表1 可知，输出构件D 位移最大值为72.139 9，最小值为－19.982 6，因此，仿真得到的最大输出位移D1D2=72.1399－（－19.982 6）= 92.122 5，该结果与前面计算所得式（9）的结果92.181 853 350 57 基本一致。

输出构件D 的速度曲线和加速度曲线分别如图5、图6 所示，从图示仿真得到的输出构件D 速度、加速度随时间变化的曲线可以看出，该六杆机构不存在冲击载荷，运行情况稳定。使用该机构进行工件的塑性挤压成形具有非常理想的工作环境，有利于提高被加工工件的精度等级。

图5 输出构件D 速度随时间的变化曲线

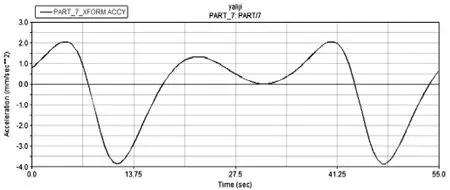
图6 输出构件D 加速度随时间的变化曲线

5 结论

文章分析了一种平面六杆机构的运动和动力，讨论了输出构件的输出行程，建立了输出行程的计算模型。 第一种情况AB、BC、CE 与机架组成的铰链四杆机构为双曲柄机构时的输出行程比较简单，直接就是CE 杆与CD 杆的长度和。 第二种情况的输出行程可以通过所建立的模型求得，文章对该情况下的机构输出行程进行了模型的仿真分析，仿真的结果与模型的结果完全相符。 机构的速度和加速度仿真结果表明该六连杆机构运动平稳性好，为该机构在机械设备中的应用前景提供了有力的证据。