基于多级网络编码的多副本云数据存储

徐光伟 史春红 冯向阳 罗 辛 石秀金 韩松桦 李 玮

(东华大学计算机科学与技术学院 上海 201620)(gwxu@dhu.edu.cn)

互联网发展带来的数据爆炸性增长，对数据存储提出了巨大挑战.企业和个人采用云存储提供的在线外包存储以获取价格低廉的海量数据存储空间.这种外包存储的最基本要求是要保证数据的可用性.目前常用的方法是通过数据备份来保证数据可用性，如多副本[1](multiple-replica)存储，通过对原始数据进行备份，一旦数据发生损坏或丢失时，可利用备份数据进行恢复.

为提高云存储的利用率和数据可用性，常采用擦除码(erasure codes)技术[2]，其中纠删码reed-solomon是一种应用广泛的擦除码[3].利用纠删码计算编码块进行冗余存储，可在相同的存储空间下获得高的数据可用性.与多副本复制相比，纠删码在相同的存储开销下提高了数据存储的可靠性[4].目前有许多改进的纠删码方法，如纠双错的极大距离可分码(maximum distance separable, MDS)[5]、EVENODD(efficient encoding on double disk failures)[6]、X-code[7]、RDP(row-diagonal parity) 码[8]、自由码(liberation code)[9]等.然而，基于纠删码的方法尽管节省了数据存储空间，但损坏数据恢复时，常因文件解码需要下载与原文件大小相同的编码块，造成大量的通信和计算开销.基于网络编码(network coding)技术[10]应用到数据备份时，通过对数据块之间的线性编码来生成数据块.损坏数据恢复时，无需解码原文件，只需下载一定量的数据块即可通过线性计算恢复原数据，从而降低了计算和通信开销.但这种方法在数据译码时，一旦数据块的编码系数存在线性相关性会导致译码失败，只能重新下载数据块，反而增加了计算和通信开销.

为降低数据存储和损坏数据恢复时的开销，本文提出一种基于多级网络编码的多副本数据(hier-archical network coding multiple replica, HC-MR)生成方法.采用多级网络编码生成多副本数据并进行分布式存储和损坏数据的恢复，本文主要贡献有3个方面：

1) 分析生成副本数据之间的关联性，建立生成副本数据块的多级编码矩阵.在生成副本数据块时，通过保证编码矩阵的满秩性来避免所生成的各编码数据块之间存在线性相关性.

2) 基于多级网络编码生成级联的多副本数据.在多级编码矩阵基础上，使得计算获得的多副本数据中的编码数据块具有唯一性.此外，采用数据副本前后级联方式计算多副本数据，使得各副本数据块之间存在特定关联性的编码关系.

3) 损坏数据恢复时，利用编码矩阵和具有级联关系的多副本数据对损坏数据进行安全恢复.对副本中的损坏数据，选择最佳的恢复副本，利用编码矩阵和具有级联关系的多副本数据进行编码计算恢复损坏数据，因无需远程下载原始数据就可恢复损坏数据，降低了计算和通信开销.

1 相关工作

为了保护数据的可用性，数据冗余技术是解决这个问题的关键技术.

1) 多副本

在分布式存储系统[11-12]中，多副本技术由于其简单、读写效率高而被广泛采用.为避免云服务商伪造副本数据，Li等人[13]和Barsoum等人[14]分别提出了利用副本及数据块编号生成随机密钥流加入到数据块计算副本文件的方法.Hou等人[15]根据副本编号对每个数据块进行加密生成副本文件，使得只有拥有密钥的数据所有者才能得到副本数据.随后，Yi等人[16]利用全同态加密计算副本数据，降低计算开销.

但多副本技术存储效率和数据容错性低且需要消耗大量的磁盘存储空间.

2) 纠删码

纠删码是对副本数据进行编码后，再存储冗余数据块，以达到容错目的.当数据损坏时，通过读取剩余的完整数据块，使用译码算法对损坏数据进行恢复.Blaum等人[6]在Raid存储体系结构中提出一种有效的双磁盘容错方案EVENODD.随后，又在EVENODD基础上提出可纠多列错的MDS阵列码G-EVENODD[17].随后，Huang等人[18]在EVENODD码基础上，提出能纠正任意3个节点故障的STAR码.然而，基于纠删码的方法，需要先恢复出原文件后才能进行数据更新或损坏数据恢复，耗费了大量的通信和计算开销.为提高数据恢复的有效性，Dimakis等人[19-20]提出一种基于网络编码的再生码(regenerating coding)用于恢复数据，它利用网络编码对纠删码进行改进来降低数据的恢复带宽.Acedanski等人[21]通过比较无编码的随机存储、传统删除码和随机线性网络编码的有效性，建立译码概率和存储、带宽之间的函数关系以减少存储开销.随后，Zakerinasab等人[22-23]提出一种减小更新带宽的网络编码方法，仅需在旧码上加个简单的码差函数即可实现更新，极大地降低了更新带宽.王龙江等人[24]也提出一种基于网络编码的云存储的差分数据更新方案，结合游程码和霍夫曼码等压缩码对差分编码块进行压缩以减少更新带宽.为适应存储和冗余需求的变化，Zhang等人[25]提出一种基于网络编码的数据存储模型，使各存储节点互相发送线性编码数据块来降低数据更新时的通信开销.为进一步降低损坏数据恢复时的通信开销，Zhou等人[26]提出了局部扩散的延迟编码算法和基于区域的重构算法，降低了部分损坏数据块恢复时的通信开销.为提高编码效率，Liu等人[27]提出一种基于图形处理单元(GPU)的纠删码实现方案，将位矩阵存储在GPU中并实现并行译码来提高编码效率.

基于纠删码和网络编码的方法，主要解决了数据容错和损坏数据恢复方面的一些问题.如何在不增加数据存储冗余的条件下，尽可能地降低开销并保证数据的可用性和安全性，还需结合副本生成和损坏数据恢复来研究其编码技术.

Fig. 1 Model ofmulti-replica data storage图1 多副本数据存储的模型

2 云多副本数据存储模型与问题

2.1 存储模型与安全威胁

云存储数据的可用性常采用多副本技术，由数据所有者在本地生成多副本数据后存储到云数据中心.典型的云多副本数据存储模型主要由数据所有者(data owner)、云服务商(cloud server)和数据使用者(data user)组成[14,16]，如图1所示.其中数据所有者生成多个副本并远程存储到云服务商的存储空间.云服务商为外包数据提供数据存储服务并保证其可用性.获得访问权限的数据使用者，通过云服务商的管理访问这些外包存储数据.

然而，外包存储并非绝对安全，因为云服务商是半不可信的[28]，即它可以“诚实的”按照协议来存储数据，也可能为了获得更高的存储效益而不按约定存够副本数.因此，云服务商会对多副本数据进行伪造攻击和隐私攻击.

1) 伪造攻击.云服务商为获取尽可能大的数据存储收益，会试图保存尽量少的数据副本.当数据使用者发起随机副本数据请求时，云服务商通过临时复制副本数据来欺骗数据使用者.

2) 隐私攻击.为实现伪造攻击或隐藏损坏数据，云服务商会在其参与数据恢复计算的过程中，收集和记录敏感的编码信息，然后通过分析，推断出副本数据之间的关联以实现伪造攻击.

2.2 问题提出

正如在相关工作和安全威胁中所分析的，半不可信的外包数据存储面临如下的一些问题.

1) 数据可用性的要求增加了数据存储和损坏数据恢复的开销.采用纠删码技术对存储数据的容错性和损坏数据恢复后的数据可用性提供保障，当损坏数据恢复时需下载并解码原文件，会增加数据所有者的计算和通信开销方面的负担.

2) 抵御云服务商伪造数据所有者的副本数据以保障数据的可用性.数据所有者存储多副本数据的目的是为了保障数据可用性，但会因云服务商的伪造副本而降低了数据的可用性.

3) 抵御损坏数据恢复时的数据编码信息泄露.损坏数据恢复时，数据所有者需向云服务商提供与损坏数据相关的编码信息.恶意云服务商会通过收集这些编码信息，分析出各副本之间编码关系，从而伪造副本数据.

多副本数据存储与恢复算法的设计目标如下：

1) 降低多副本数据存储和损坏数据恢复时的开销.

2) 数据存储和损坏数据恢复过程中抵御安全攻击的威胁.

3 基于多级网络编码的多副本存储和损坏数据恢复

本文在纠删码技术基础上，结合多级网络编码设计了基于多级网络编码的多副本数据，用于副本数据存储和损坏数据的恢复.

多级网络编码(hierarchical network coding)由Nguyen等人[29]提出，其原理是，若一个数据流被划分为多个数据块，每个数据块属于A，B，C分类中的一类.其中，A类数据块最重要，B类次之，C类最不重要，记为A>B>C.假设该数据流共有6个数据块，分别记为a1,a2,b1,b2,c1,c2，其中a1,a2属于A类，b1,b2属于B类，c1,c2属于C类，则多级网络编码的构造方案为

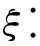
3.1 多副本数据的生成

3.1.1 数据加密及分割

数据所有者对原文件进行加密并分割成数据块.加密使用密钥采用对称加密方式.设原文件为F*，加密后的文件为F.然后，对加密文件F进行分割得到n个数据块b1,b2,…,bn.

3.1.2 利用多级编码矩阵建立数据块的编码

纠删码(n,m)在计算m个冗余码时，将n个原数据块按列排成向量，构成一个(n+m)×n的分布矩阵B.对于矩阵B，它的任意n个行向量都是相互独立的，即这n个行向量组成n×n矩阵是可逆的.矩阵B的前n行是单位矩阵，后m行基于范德蒙矩阵构造.

本文在继承纠删码的线性编码的优点基础上，采用多级网络编码对矩阵B的后m行进行改进，提出一种多级编码矩阵.

定义1.矩阵的线性无关性.矩阵中任一向量，都不能由矩阵中其他向量进行线性表示.矩阵的行初等变换不改变列向量之间的线性关系.

定义2.多级编码矩阵(hierarchical coding matric).对于一个a×b的矩阵L，从第一行开始，以b为单位组成一个小方阵，使得每一个方阵的行向量中不为0的数依次递增，且每个方阵都由前一个方阵通过矩阵初等变换得到，并且所有小方阵都具有满秩性，其中a为大于0的正整数，b为大于3的正整数且为奇数.

假设有n个数据块，需计算m-n个冗余码，则构建一个m×n的编码矩阵.让正整数k≤n-1，其中n≥3，且m=s×n.为降低编码矩阵的计算量，让矩阵前n行即第1个矩阵对角线上的值全部为1.多级编码矩阵L由s个n阶方阵Lk(k∈[1,s])组成，如式(1)所示：

(1)

式(1)的具体构造方式如下：当k=1时，矩阵L1中的各元素为

(2)

当k>1时，其余s-1个n阶方阵Lk的各元素为

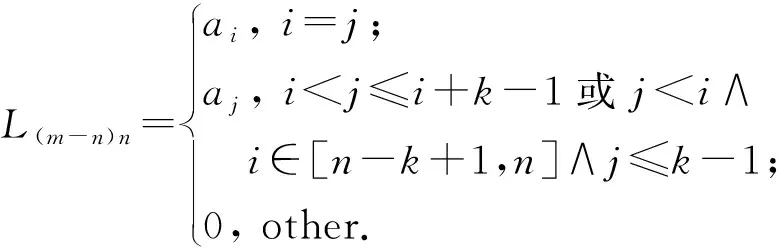
(3)

其中，i∈[1,n]，j∈[1,n]，k∈[2,s].当s取最大值n-1时，可得式(1)中的

(4)

(5)

(6)

其中ai由数据所有者利用矩阵密钥t和随机函数生成.通过多级编码矩阵计算的编码被称为多级编码(hierarchical coding, HC).

3.1.3 副本数据的多级编码

利用所建立的多级编码矩阵L，通过多级编码生成副本数据.假设文件F需要生成s个副本，每个副本包含n个数据块，且n为不小于3的非偶数.编码后得到s×n个数据块，其中每个副本的多级编码矩阵为n行n列的方阵.具体编码过程为：

1) 数据所有者从有限域中选取矩阵密钥t，通过随机函数得到n个元素ai，其中每个元素ai互不相等且不为0.然后构造成一个(n×s)×n的多级编码矩阵L.

2) 为计算s个副本，应用式(1)～(4)分解多级编码矩阵L，用lki表示矩阵Lk中的每个行向量，可得s个副本对应的n行n列的多级编码矩阵Lk为

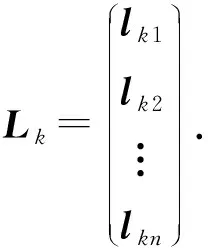
(7)

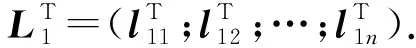
多级编码矩阵具有以下特性：①极大距离可分码性，即多级编码矩阵的线性无关性，使得任选n个编码数据块都可有效参与编码数据块的解码计算；②独特性，即各副本的多级编码矩阵都是满秩矩阵，每个副本中编码数据块彼此都不相同；③关联性，即每个编码数据块都由其他编码数据块通过编码计算得到，也就与其他编码数据块之间存在一定的计算关系.

3) 利用Lk计算基于多级网络编码的多副本文件.对于副本Fk，当副本编号k=1时，可由副本F1的数据块向量Z1=(b1,b2,…,bn)与编码矩阵L1计算来生成数据块编码，即

(8)

以此类推，可由副本文件Fk-1与Lk计算得到副本Fk的数据块编码为

(9)

Fig. 2 Multi-replicas are generated based on hierarchical network coding图2 基于多级网络编码生成多副本文件

3.1.4 数据存储

数据所有者计算出所有副本文件后，将其上传到云服务商的数据中心(多个存储节点)进行分布式存储，编码矩阵由数据所有者秘密保存.

参考目前普遍采用的3副本存储模式[14]，让s=3，F=(b1,b2,b3,b4,b5)，利用编码矩阵计算15个数据块b11,b12,b13,b14,b15,b21,b22,b23,b24,b25,b31,b32,b33,b34,b35.可得3个副本文件F1=(b11,b12,…,b15)，F2=(b21,b22,…,b25)，F3=(b31,b32,…,b35).

基于多级网络编码的多副本文件生成算法(HC-MR)如算法1所示：

算法1.HC-MR算法.

输入：原文件F，原文件加密密钥x，矩阵生成密钥t，副本数s；

输出：s个副本文件Fk(k=1,2,…,s).

① 初始化密钥参数(x，t)；

② (x,t)←Genkey(·);*生成密钥*

③F←encrypt(F*,x);*对文件加密*

④ (b1,b2,…,bn)←devide(F);

⑤ fork=1;k≤s;k++ do

⑥Lk←createMatric(t);

⑦Fk←Genreplica(Fk-1,Lk);

⑧ end for

⑨ returnFk(k=1,2,…,s).

3.2 损坏数据的恢复

损坏数据的恢复需要利用其编码系数与特定的副本数据进行编码计算来恢复.此外，为避免编码信息泄露而导致副本文件被伪造，需对编码信息进行隐藏.具体过程如下:

1) 损坏数据块的编码信息计算

Fig. 3 Recovery of corrupted data图3 损坏数据的恢复

首先，检测损坏数据的副本编号.通过数据完整性验证[30]发现数据bki损坏后，获得其所在的副本编号k.然后，选择恢复损坏数据的最佳副本文件.通过选择最佳副本，以最小的计算开销恢复损坏的副本.

假设副本Fk中的数据块bki损坏.若k≠1时，应用式(9)可知Fk=LkFk-1.因此，选择Fk-1为最佳副本，并计算第k个副本的多级编码矩阵Lk，再根据副本Fk中的损坏数据bki选择Lk中第i个行向量lki.

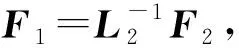
2) 数据恢复编码信息的加密

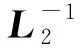
3) 损坏数据的恢复

云服务商收到损坏数据恢复请求Q后，读取本地副本文件与其计算即可恢复损坏的数据：

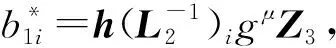
最后，利用文献[31]的方法对云服务商延迟或不恢复损坏数据进行检测，此处不再赘述.

基于多级网络编码的损坏数据恢复算法(DR)描述算法2所示：

算法2.DR算法.

输入：矩阵生成密钥t、编码信息密钥μ、损坏数据的副本编号k、损坏数据块的序号i；

①sk=μ←genkey(μ);

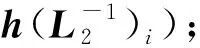
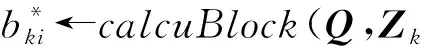
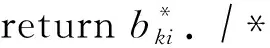
4 算法安全性及计算复杂性分析

4.1 安全性分析

1) 正确性分析

2) 抵御编码信息的泄露

HC-MR可抵御云服务商收集数据恢复编码信息Q以获得数据块的编码信息lki，并还原出Lk.

3) 抵御伪造攻击

HC-MR可抵御云服务商的伪造攻击，即保存较少数量的副本，当数据所有者发起随机副本数据请求时，临时复制副本来响应.

4.2 计算复杂性分析

本节主要分析基于多级网络编码的多副本存储和损坏数据恢复的时间开销.

设生成多级编码矩阵的计算开销为THCM，需要计算s个副本.采用纠删码时，只需要确定编码块数，就可确定编码矩阵的大小，其编码矩阵的计算开销为THCM.此外，利用纠删码计算副本的编码数据块时，直接利用编码矩阵，选取随机数对数据块进行线性计算即可得到编码块，因此，计算3个副本的时间复杂度为TMul=O(n3).而HC-MR中多级编码矩阵数量与副本数成正比，多级编码矩阵的计算开销为s×THCM.此外，HC-MR在数据编码计算前需要生成副本的编码矩阵，即输入密钥，生成多级编码矩阵，再基于多级网络编码进行多副本数据的计算，时间复杂度为THC-MR=O(n3).

若n个数据块中num个发生损坏.利用纠删码进行损坏数据恢复时，需要先从云存储空间中下载n个编码数据块，通过解码得到原始数据块，再利用矩阵生成算法计算编码块的编码矩阵，最后对损坏的数据块再重新进行编码计算，其时间复杂度为TRS=num×O(n3).采用网络编码方法，为避免恢复用的编码数据块与其他数据块间存在线性相关性，需要进行多次的多个完整编码数据块的线性计算，其时间复杂度为TNC=num×O(n3).而HC-MR方法，首先判断每个损坏数据块所在的副本位置，其时间复杂度为O(n).然后计算副本的多级编码矩阵Lk，其时间复杂度为O(n).最后再利用编码信息与相应副本计算进行损坏数据恢复.因此，其时间复杂度为THC-MR=num×O(n3)，3种方法的时间复杂度相同.

4.3 容错能力及数据可用性分析

1) 容错能力

容错能力指所存储的编码块可恢复出原始文件的最大容忍出错的块数[32].设e为原始数据块数，p为数据冗余度.基于纠删码方法和本文的HC-MR，共存储编码块为p×e.由于只需e个编码块就可恢复原文件，所以其容错能力是(p-1)×e.基于网络编码的方法，因其编码块间可能存在线性相关性,设γ为相关系数，则其容错能力为(p-1)e(1-γ).其数据容错能力随着γ的增大而降低.当γ=0时，3种方法的容错能力相等.

2) 数据可用性

数据可用性指存储数据可正常使用的概率，用β表示.在数据冗余度p下，系统中有p×e个数据块，其中冗余数据块为(p-1)×e.根据文献[32]，基于纠删码方法和本文HC-MR的数据可用性为

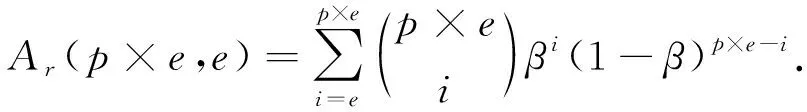
(10)

基于网络编码方法的数据可用性为

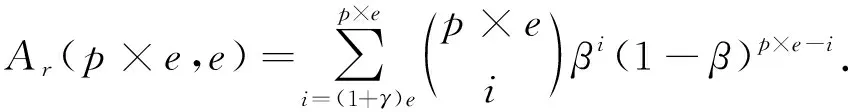
(11)

参考容错能力的分析可知，当γ=0时，基于网络编码方法中编码块间不具有线性关系，此时3种存储策略的容错能力相等，但随着γ的增大，基于网络编码方法的数据可用性逐渐降低.

5 实验及性能分析

为了测试算法的性能，使用一台Intel Core i7处理器1.99 GHz，8 GB内存的笔记本电脑作为数据所有者.租用阿里云服务器的8核CPU，16 GB内存，40 GB存储系统来模拟云服务商.实验中各算法采用Java编写，实验代码在Reed-Solomon-error-correction-1.2基础上修改.数据编码在有限域GF(216)中进行，将文件数据拆成字长16位后进行编码计算.本文方案HC-MR与文献[25]的NCScale和文献[27]的G-CRS方案进行对比，并分别从副本生成的存储、计算和损坏数据恢复的计算、通信开销等方面进行性能分析.

5.1 副本生成的计算和存储开销

选取文件大小为1 MB，10 MB，20 MB，30 MB，40 MB，50 MB，60 MB，70 MB，80 MB，90 MB，100 MB，3种方案生成副本的计算开销如图4所示.可以看出HC-MR与G-CRS，NCScale的计算开销相近，且3种方案生成副本的计算开销随着副本数的增加也相应的增加.其中HC-MR略微偏高，其原因是，在进行副本生成时，需先生成多级编码矩阵，再进行副本计算，而NCScale和G-CRS方案则无需计算每个副本的编码矩阵，因此，它们的计算开销略小.此外，考虑到G-CRS采用了GPU计算，在有限域GF(24)中取线程数为128时，也测试了其开销.可以看出，G-CRS(GPU)相对于HC-MR显著减少了计算时间.这是因为G-CRS(GPU)将矩阵存储在GPU的存储器中实现同一编码矩阵的并行编译码.

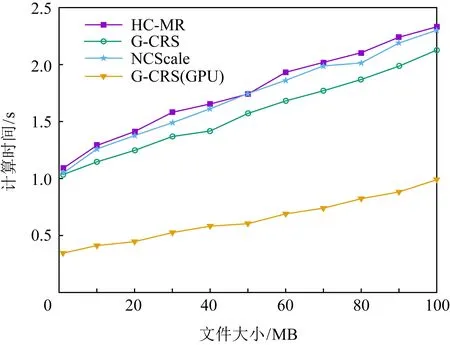
Fig. 4 Computation time for replicas generation图4 副本生成的计算时间

选取文件大小为1 MB，10 MB，20 MB，30 MB，40 MB，50 MB，3种方案存储3个副本的存储开销如图5所示，可以看出他们的存储开销是相同的.这是因为3种方案在编码计算前，为避免编码计算后的数据块增大而出现溢出，副本分块时按照文献[33]的方法选择数据块进行编码.

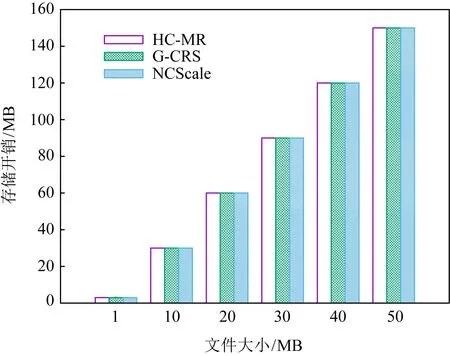
Fig. 5 Replicas generated storage overhead图5 副本生成的存储开销

5.2 损坏数据恢复的计算和通信开销

损坏数据恢复时，3种方案的计算开销如图6所示，其中图6(a)和图6(b)分别为数据所有者和云服务商的计算时间.由于G-CRS和NCScale只涉及数据所有者的计算，所以图6(b)的值都为0.综合来看，HC-MR的计算开销比G-CRS和NCScale略大.这是因为G-CRS只对编码数据块解码后，计算损坏数据的编码.NCSale需下载尽可能多的编码块通过线性计算来恢复，而无需解码计算.HC-MR需要提供与损坏数据相关的数据编码向量，以及与损坏数据相关的副本，然后进行编码计算进行恢复.此外，HC-MR在矩阵求逆前，还要生成多级编码矩阵，所以计算开销略大.

Fig. 6 Corrupted data recovery time图6 损坏数据恢复的时间

取文件大小为10 MB，30 MB，50 MB，90 MB，100 MB，让副本数为3，这3种方案的损坏数据恢复的通信开销如图7所示，其中G-CRS的通信开销最大，NCScale次之，HC-MR最小.其原因是，G-CRS需要先恢复出完整的副本文件后，才能恢复损坏的数据块，而无论有多少损坏数据，都需要下载完整的副本.NCScale若下载的数据块具有线性关系而不可用，又因编码块间线性关系的不确定性，而需下载尽可能多的编码块.HC-MR的编码矩阵具有满秩性和编码块间的线性无关性，数据恢复时只传输编码向量即可.

Fig. 7 Communication overhead when recovering data图7 恢复数据时通信开销

5.3 数据可用性和容错能力

选取副本数为2，3，4，5，6，7，8，HC-MR，G-CRS，NCScale(γ分别取0%，30%，100%)比较如图8所示.当副本数较少即数据冗余度较小时，HC-MR，G-CRS，NCScale(γ=0%)三种算法的曲线重合且数据可用性较高，NCScale(γ=30%)次之，NCScale(γ=100%)最低.随着数据冗余度增加，3种方案的数据可用性都增加.当副本数为7时，3种方案的数据可用性趋于一致.其原因是，数据冗余度较小时，HC-MR，G-CRS，NCScale(γ=0%)允许任意数据块发生损坏并恢复，而NCScale(γ=100%)因冗余的编码块间具有线性相关性，只能恢复特定的数据块，即每个副本中相同编号的数据块，导致可用性最低.

Fig. 8 Data availability图8 数据可用性

选取原文件大小为1 MB，3种方案的数据容错能力如图9所示.在相同副本数下，HC-MR，G-CRS，NCScale(γ=0%)三种算法的曲线重合且有较高的容错能力，NCScale(γ=30%)次之，NCScale(γ=100%)最低.其原因是副本数增加时，HC-MR，G-CRS，NCScale(γ=0%)可有效恢复任意损坏编码块，而NCScale(γ=30%)只能恢复部分不存在线性相关的损坏数据.NCScale(γ=100%)因编码块间的线性相关性，无法恢复损坏数据.

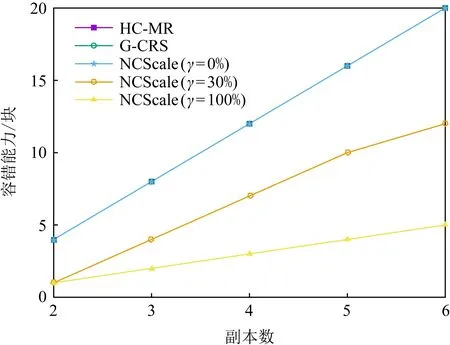
Fig. 9 Data fault tolerance图9 数据的容错能力

通过上述实验，可以看出，HC-MR的副本生成的计算和存储开销与G-CRS(不采用GPU)和NCScale相近；损坏数据恢复时的计算开销比G-CRS和NCScale略大，而通信开销最小；当副本数较少时，HC-MR与G-CRS的数据可用性较高；当副本数相同时，HC-MR和G-CRS的容错能力较高.因此，HC-MR在提高数据可用性的同时，也减少了损坏数据恢复时的通信开销.

6 总 结

云存储数据备份应以尽量少的存储空间来满足最大的数据可用性，本文提出了一种基于多级网络编码的多副本数据备份方案.利用多级编码矩阵生成副本数据块，然后基于多级编码生成级联的多副本数据，最后利用数据所有者提供的损坏数据的编码向量，与存储节点上保存的副本数据进行计算从而恢复损坏数据.与现有方案相比，提高了数据的可用性，并减少了损坏数据恢复时的通信开销.未来，将进一步优化数据的编码和解码，以及编解码计算的效率.