一种基于区块链的泛用型数据隐私保护的安全多方计算协议

刘 峰 杨 杰 李志斌 齐佳音

1(华东师范大学计算机科学与技术学院 上海 200062)2(上海对外经贸大学人工智能与变革管理研究院 上海 200336)3(华东师范大学数据科学与工程学院 上海 200062)(lsttoy@163.com)

自中本聪2008年提出比特币以来，区块链作为一种跨行业应用的突破性底层技术，得到了飞速的发展.与大数据、云计算、人工智能等当前流行的信息技术相比，区块链去中心化、难篡改、可追溯、公开透明等特性更能满足人们日益增长的需求[1].然而，随着学界研究的不断深入，越来越多学者发现，在基于区块链技术的去中心化账本中用户的信息是很容易被追踪的.陈伟利等人[2]就通过研究发现，用户隐私信息的窃取与其用户地址信息的泄露多少是有很大关联的.基于环签名的数字货币门罗币，也曾被Möser等人[3]通过追踪用户签名私钥的方式攻破了隐藏交易，从而对交易发起人的隐私信息造成了很大的威胁.除此之外，大多数区块链交易所也都集成了中心化身份验证机制，用户的个人信息和区块链的地址之间映射关系会理所当然地被交易所记录下来.在大数据技术运用下，用户的交易信息和行为被破解的风险也就会激增.2017年Ermilov等人就利用自动聚类法分析出用户与其比特币地址间的关联关系，提出了用户不安全的比特币使用模式[4].

因此，区块链技术的安全问题也越来越受到重视.如何合理高效地做到用户身份信息及交易数据的隐私保护是当前区块链技术领域在安全方面的一个关键问题.如在医疗健康服务行业，如何安全高效地解决个人医疗健康数据共享问题同时保证个人数据的隐私；再如在货运物流行业，如何与多方货物供应商快速建立信任关系，保证优质长尾资源同时确保交易信息不被窃取篡改等.随着技术的不断更新与迭代，安全多方计算的出现为解决此类问题提供了可能途径.

在当前区块链安全多方计算的研究中，区块链科技服务商Defi利用区块链以及可信计算搭建了帮助企业能够实现联合风控的系统架构，但效率、透明度上还存在一些问题；宋俊典等人[5]提出了一种基于区块链的数据治理协同方法，并给出多方协作的构建标准以实现区块链协同治理，但是隐私安全上却并没有给出较为具体的分析策略.结合上述文献并从当前技术发展趋势来看，要提升效率的同时做到有效的隐私保护，设计一种匿名条件下对多方消息进行合并签署并高效验签的安全多方计算协议势在必行.其实早在2001年就出现了可对不同消息进行合并签署并验证的BLS方案[6]，并且近些年该方案主要提出者Boneh教授仍在更新这种签名方案[7]以适配当前安全多方计算的研究发展.不过由于BLS签名自身独有的运算逻辑导致其过于依赖有限域中椭圆曲线上的双线性对(bilinear pairing)运算且运算次数较多[8-9]，这导致在相同签名条件下，BLS签名甚至要比当前以太坊(Ethereum)广泛使用的ECDSA签名验签花费的时间成本多上3倍.

本文在已有的研究基础上，为了对不同消息进行合并签署并验证，在现有聚合签名基础上提升签名验签的效率，同时加强敏感数据的隐私性和匿名性，参照了Yu的Pedersen承诺加Schnorr签名方案[10]，设计出了BPLSM协议，一种区块链上融合Pedersen承诺与Schnorr协议的安全多方计算协议.通过对该协议进行形式化验证，证明了BPLSM协议能确保信息在不被泄露情况下证实签名的合法有效.在此之后，利用此协议设计相关实验构建了一个半诚实者模型下的签名验签程序.实验主体逻辑是通过对验签不通过的签名进行舍弃，验签通过的抽离出相关签名信息交由链上合约使用承诺时的盲因子和宣告进行解析，得出统和意见后处理事务并公布结果，保证签署消息的合理性、匿名验签的高效可行性.实验结果证明，在相同验签条件下基于BPLSM协议构建的签名比BLS签名在验签上能节省约83.5%的时间成本.

1 基础知识

本节主要介绍协议所涉及的基础知识，包括Pedersen承诺、Schnorr协议以及安全多方计算.

1.1 Pedersen承诺

目前隐私保护方案中使用较为广泛的密码学承诺之一便是Pedersen承诺[11].与常见的Hash承诺相比，Pedersen承诺具备同态特性，可直接对密文消息进行操作，即无需破坏敏感数据源就能实现隐匿计算.

在区块链中，椭圆曲线加密(Elliptic Curve Cryptography, ECC)是基础技术之一.而基于椭圆曲线的Pedersen承诺[12]则是一种构造范围证明的重要手段.对于一次Pedersen承诺，示证者A向验证者B发出关于隐私消息m的承诺后，再由B验证承诺合法性的过程如图1所示.从图1中可以看出，该承诺实现方式为：承诺的准备阶段在椭圆曲线上选取2个以某个大素数p为阶的基点G,H，作为承诺生成时的公共参数.然后在承诺的产生阶段，由A产生一个随机数seed，通过seed按照如下公式计算承诺Commitment并将其发送给B：

Commitment=m*G+seed*H,

(1)

其中，*表示有限域上离散对数运算的二元关系.

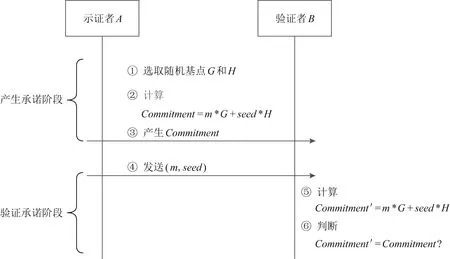
Fig. 1 Pedersen commitment interaction process based on elliptic curve图1 基于椭圆曲线的Pedersen承诺交互过程

在验证阶段，B将会再次接受A从匿名信道发送过来的验证参数对(m，seed)并按照式(1)计算承诺Commitment′.通过比较Commitment与Commitment′是否相等即可判断承诺是否正确合法.在此过程中，对于验证者B，表征在区块链上就是一个验证承诺的智能合约，也就是由合约获取验证参数进行承诺验证，在一定程度上保证公示结果正确不被篡改.

至于应用方面，Pedersen承诺在当前的基于Mimblewimble协议的交易输出中包含了约33 B的Pedersen承诺内容以实现保密交易，并结合Bullet-Proofs的零知识证明体系消除对地址和私钥依赖以实现轻量级的隐私保护[13-14].Pedersen承诺已在数值隐藏、恒等关系验证以及审计验证等方面发挥着不可或缺的作用.

1.2 Schnorr协议

作为Sigma协议(Σ-protocol)的一种，非交互式的Schnorr协议[15]是一个非常优秀、简洁且具备零知识性的安全协议.虽然Schnorr协议于1989年就被提出，但数十年来学界对其探索、研究的热情丝毫未减，近年来在区块链领域更是大展身手.如零知识数据交换协议zkPoD中，为了另辟蹊径实现公平交互(fair exchange)，就利用了一个扩展的Schnorr协议结合Pedersen承诺去实现高效性和可扩展性[16].在Schnorr协议研究发展中，各种Schnorr聚合签名扩展了密码学椭圆曲线数字签名的方案，推动了数字签名的发展.Maxwell等人在2019年的文献中，也提出基于Schnorr协议的多重签名方式，并应用到比特币网络中[17].

Schnorr聚合签名可以分为密钥生成、密钥集聚和、交互随机数、生成单一签名、聚合签名以及验证签名6个步骤.交互过程如图2所示.

以3个签名者聚合签名为例，首先需要彼此之间交换各自的随机数，然后利用各自的签名私钥分别对同一消息进行单一签名，接着就是对单一签名进行聚合，生成一个新签名，最后交由验证者利用验证密钥进行验证.在此过程中，对于验证者，表征在区块链上就是一个验证签名的智能合约，由合约利用预定义的验证密钥对组合签名进行验证，保证签名的合法性.

根据先行研究结合上图签名逻辑，不难看出对单一消息的单一签名或者聚合签名，Schnorr协议在签名方案上已经非常成熟.

Fig. 2 Schnorr aggregate signature interaction process图2 Schnorr聚合签名的交互过程

1.3 安全多方计算

安全多方计算主要目的是解决互不信任的参与方在保护隐私的前提下协同计算的难题[18].相比传统的数据保密，安全多方计算的优势如表1所示：

Table 1 Comparison of Traditional Data Confidentiality and Secure Multi-Party Computation表1 传统数据保密与安全多方计算的比较

在信息飞速发展的今天，协作情境的出现已经屡见不鲜.安全多方计算输入隐私性、计算正确性以及去中心化性的技术特点正好满足了在这样的场景下参与方希望得到合作利益却又不希望泄露自己数据的客观需求.所以，近年来安全多方计算的研究也在不断深入.Zhu等人[19]在2018年采用动态规划的方法改进了常数轮的多方计算协议，提升了运算效率.周俊等人[20]也曾在边缘计算中分析过电子医疗系统中运用安全多方计算时进行隐私保护，并权衡计算开销.Hastings等人[21]更是在安全顶级会议Security and Privacy 2019上详尽分析了多个安全多方计算通用框架，并在docker中将构建环境进行了打包，从各个维度评估了这些框架的优劣.

当然，随着数据隐私问题日益明显，区块链与安全多方计算的结合也开始被纳入加强隐私保护的范畴内.区块链因区块数据难被篡改的特征往往更加强调计算的可验证性而不考虑输入信息的保密性.而安全多方计算则强调的是多方计算过程中对消息的保密性但不能确保数据的可验证性.故二者可进行优势互补，一方面区块链利用安全多方计算提升隐私能力，以便于实施到更多的应用场景中；另一方面，安全多方计算可借助区块链技术进行公开透明不被篡改的交易验证.如智慧医疗、舆情存证、拍卖清算等应用场景上的隐私保护与高效事务处理问题，2种技术的正交为加快分布式网络中的数据隐私保护提供了可能.

2 安全多方计算协议BPLSM

本节先提出安全多方计算签名的现状引出BPLSM协议，然后从BPLSM的架构设计入手，阐释该协议主要的3个性质并分析其安全性.

2.1 安全多方计算单一签名现状

一个简单的基于区块链的安全多方计算的单一签名实现如图3所示：

Fig. 3 Single signature based on secure multi-party computation图3 基于安全多方计算的单一签名

从图3中可以看出签名参与方在链下进行协作签名且只产生一个统一签名交由链上合约对其验证，判断合法性.而在一些多方计算场景中，参与方的选择可能是多向的，比如投票选举中参与方投同意票或者否决票、交易仲裁中参与方同意返还资金给买家或者释放资金给卖家等.面对这样的多方参与的情形，单一消息的统一签名往往并不能满足需求.

因此在保证安全的前提下提升一定的效率是能够应用的关键.本文考虑使用具有同态加法特性的Pedersen承诺对Schnorr协议进行改进，提出了能够实现对多种不同消息进行聚合签名并具备在区块链上进行高效验签能力的BPLSM协议.

2.2 BPLSM协议架构

本协议的架构设计图如图4所示.从图4中可以看出，首先第一步各签名参与方进行隐匿消息承诺，公式如下所示：

MCommitmenti=mi*G+seedi*H,

(2)

其中:G和H为有限域椭圆曲线上2个位置不同的固定点;mi为各方签署的互异消息;seedi为随机数种子，i∈{1,2,3}.在作出敏感消息的承诺MCommitmenti后，需要将参与三方的消息承诺进行聚合，以便生成一个统一的签名，交由合约验证.

Fig. 4 BPLSM protocol architecture图4 BPLSM协议架构

有关签名相应的步骤以及计算如下：

1) 参与三方按式(2)生成各自的承诺MCommitment1,MCommitment2和MCommitment3；

2) 各方分别私下生成盲因子r1，r2，r3，并互相公开r1*H，r2*H，r3*H，作为基于盲因子ri的公钥Ri，i∈{1,2,3}；

3) 根据各自公开的公钥Ri，定义组合的消息承诺:

(3)

各方将计算得出的组合交易承诺进行Schnorr签名，即SigMi=ri+SumCom*prkeyi，其中prkeyi为各方的私钥.并把各自交易宣告declarei，以及使用的seedi通过一个匿名信道分别传给合约，i∈{1,2,3}；

4) 各方将各自交易的签名交给最后签名的一方进行聚合签名

SigM=SigM1+SigM2+SigM3,

(4)

5) 聚合完成之后，由最后签名的一方将单一签名对(R,SigM,MCommitment)提交到合约，其中R=R1+R2+R3.

上述协议签名步骤，通过利用Pedersen加法同态的特性，在不解密各方交易承诺的条件下，直接对密文形式的交易承诺进行组合运算，使得参与三方消息承诺都加入到隐私计算之中，保证了各方在匿名条件下的发言权.此外，因为最后提交到合约的是一个单一签名，所以也减少了合约签名验算的时间，避免了不必要的计算开销.

值得一提的是，具体方案设计中，相关签名参与方是在链下完成业务交互后，将对应的数值变化表达成Pedersen承诺，再对承诺数据进行Schnorr签名进行上链操作，这个过程中无需披露任何隐私数据明文.而上链之后，虽然区块链分布式网络中第三方难以通过Pedersen承诺的密文形式反推出隐私数据明文，但是可验证承诺间的约束关系、签名的有效性以及核实业务交互的合法性.

2.3 BPLSM协议的3个性质

为了证实研究方法中隐私计算的三大交互性质，本节从完备性、可靠性以及零知识性上进行分析.

2.3.1 完备性

诚实的参与方会按照链下签名逻辑，先生成自己的消息承诺；然后接受其他参与方的消息承诺，计算组合的承诺并进行签名；最后向合约宣告自己的消息，整个过程并不会向其他参与方泄露自己签名的承诺，确保了方案流程的完备性.

2.3.2 可靠性

从整个协议隐私加密过程中链上承诺验证和签名验证这2个方面的安全性进行分析.关于承诺的验证是否可靠，可以根据式(1)推导验证：

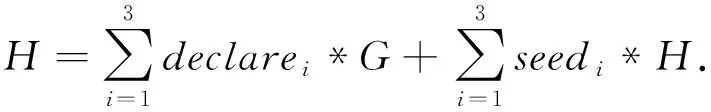
(5)

如果式(5)能够成立，则说明最后提交承诺合法，承诺是可靠的.而关于签名的验证是否可靠，可根据式(6)进行推导验证：

(6)

如果式(6)能够成立，则表明签名可靠.各参与方在各方互相公开公钥Ri前，对需要进行Hash的组合承诺MCommitment是没有办法预测的，即使这个组合承诺最终是参与方自己计算的，但参与方并没有能力通过挑选SumCom实现作弊，因为只要Ri公示之后组合承诺就被固定下来了.

最后，为防止参与方的真实地址会在验签结束后被使用的匿名地址所追溯，在每次验签结束之后，匿名地址就会被销毁.

2.3.3 零知识性

链上基于Pedersen承诺的隐藏性，在合约未验证前任何人都无法从承诺中获取任何有关的敏感数据信息.此外，合约进行验证时，除了最终的聚合签名和参与方的共同公钥，并没有传输大量的数据，验证简洁.

对于多方计算进行组合承诺时，各参与方并未暴露自己用于承诺的随机数seedi，且一方无法通过作弊手段获取另一方私钥，即无法学习到有关单个Pedersen承诺内的任何知识，该协议对每个参与方来说是零知识的.

2.4 安全性分析

链下实现多重签名相比链上实现多重签名而言安全性会更高，主要是前者更依赖于密码学算法，后者更依赖于智能合约，而智能合约在设计上可能会存在漏洞，也就容易存在安全隐患.另外，由于不是每个参与方都需要与合约进行频繁交互，且用户地址均已匿名，因而也就降低了用户被攻击的风险.安全多方计算中还需要考虑以下3种攻击者模型.

1) 在诚实者模型中，诚实的参与方总是能够按照设计准则提供正确交易承诺和签名，且不窃取其他参与方输入.

2) 在半诚实者模型中，半诚实参与方按规则提供正确交易承诺，但试图窃取其他参与方交易承诺的内容.因为单个交易的消息是按Pedersen承诺进行处理的，所以半诚实的参与方要想窃取其他参与方的交易承诺，需要拿到其他参与方生成的随机数种子seed.但是seed是由各参与方秘密保管的，且每次签名验签时只使用一次，所以只要参与方不串谋就不可能被轻易获取.另外，对于各参与方的交易签名，半诚实参与方因为无法获取交易签名中的盲因子ri以及用户私钥prkeyi，所以交易签名的具体内容也是很难被窃取的.

3) 对于恶意攻击模型，恶意参与方可能会提供虚假隐私消息承诺的签名，并试图窃取、更改其他参与方隐私交易承诺和结果.比如在存在一个恶意参与方的多方计算中，恶意参与方会提交虚假的承诺，然后使得参与三方组合承诺的计算值不一致，从而破坏签名验签的合法流程.本研究方法并不适用于恶意攻击模型.

此外，借助Pedersen承诺对签名的承诺内容进行加密保证，使得任何参与方在合约宣布验签结果前都不会知晓组合承诺内容，以应对攻击者可能的提前终止行为.所以总的来说，对于需要在数据密文形式上直接进行运算和交叉验证的业务，只要不涉及互不透露数据明文的多方协同计算，相比现有的同态加密算法，以Pedersen承诺为代表的密码学承诺往往可以提供更好的性能.

3 验证与模拟实验

为证实BPLSM协议的可行性，本研究以Go语言和Solidity语言为主，设计了BPLSM协议实验.为了在签名验签流程上体现出BPLSM协议高效的客观性，本研究在同等硬件环境下对当前可签署不同消息的主流聚合签名之一的BLS签名进行计算开销对比实验.相关实现代码以及测试代码参照本页注脚(1)实验测试代码地址：https://github.com/york-yang-me/BPLSM-Protocol.实验运行的硬件环境如下：

内存：8核8 GB;CPU：intel i7 2.60 GHz;硬盘：448 GB;系统运行环境：windows10家庭版.

补充说明一点，之所以选择Go语言进行仿真实验编码的首选语言是因为Go语言开发效率高、执行性能好且支持并发，所以利用Go语言来编写链下测试代码模拟多方协同签名消息是非常方便的.此外Go语言自带的单体测试和压力测试功能，也省去了编写测试签名的繁琐代码的时间.实验中以3个参与方为基准，构建的BPLSM协议实验的聚合签名效率与基于BLS12-381曲线构建的BLS签名效率的比较信息如图5所示：

Fig. 5 BPLSM protocol and BLS signature stress test information图5 BPLSM协议签名与BLS签名压力测试信息

从图5中不难看出，相同硬件环境下，利用Go语言对BPLSM协议签名进压力测试平均消耗的时间比(组合承诺生成时间加上聚合签名时间)BLS签名的平均消耗时间要少.

为了更加清晰地查看结果，将图5上终端测试信息归总为如表2所示:

Table 2 BPLSM Protocol and BLS Signature Stress Test表2 BPLSM协议签名与BLS签名压力测试

因为BPLSM协议的签名过程分为组合承诺的生成和聚合签名的生成，所以需要在压力测试过程中分成2块进行分析，而BLS签名需要多方参与聚合过程只有一次，所以压力测试的时候只需要对聚合签名进行测压.从表2中可以看出同等测压情况下，BPLSM协议签名时间开销成本比BLS签名低，但是如果撇开效率问题，BPLSM协议牵扯到了2次多方交互的过程，所以签名的比较还存在一些局限性.因为存在不可控的环境因素，详细分析请参照4.1节.

验签过程需要通过智能合约在区块链上执行，所以本实验中用Solidity语言在Ganache私有链上实现与Go语言中签名内容相适配的验签逻辑.并通过使用truffle框架结合Javascript脚本语言进行验签效率的分析.仍然以3个参与方为基准，给出利用truffle框架结合Javascript脚本语言构建BPLSM协议验签部分与基于BLS12-381曲线的BLS验签部分.单次实验验签测试的信息比较如图6所示：

Fig. 6 BPLSM protocol verification and BLS signature verification test information图6 BPLSM协议验签与BLS签名验签测试信息

从图6中不难看出，在测试过程中BPLSM协议验签时间为186 ms，而BLS协议验签时间却为2 880 ms.二者验签测试结果差异很大.

为了能更加准确地对两者在以太坊智能合约验签上进行效率比对，从而证实设计的BPLSM协议的优势.我们再次对BPLSM协议验签部分和基于BLS12-381曲线的BLS验签部分分别进行20次单体测试，以便加强实验的说服力.如表3所示:

Table 3 BPLSM Protocol and BLS Signature Verification Test表3 BPLSM协议与BLS验签测试 ms

从表3中可以看出，本研究设计的BPLSM协议在参与三方中的平均验签时间约为几百毫秒，而BLS签名的平均验签时间约几千毫秒，也就是说同等实验环境中BPLSM协议在验签效率上要比BLS签名花费的时间成本少，且无需进行多次单公钥签名消息比较即可验算结果.

为客观详实展现实验现象，图7以两者的平均验签时间损耗相比较.可以看出，对于该实验中参与三方的多方计算中，BPLSM的平均验签时间为260.8 ms，而BLS的平均验签时间为2 908.8 ms.BPLSM协议验签时间成本损耗比BLS签名验签节省了约83.5%.

Fig. 7 The average verification efficiency between BPLSM protocol and BLS signature图7 BPLSM协议与BLS签名平均验签效率

4 讨 论

4.1 算力开销

多方协作的签名组合放在链下执行相比在以太坊合约中设计多重签名的逻辑而言，利用安全多方计算来提交单一的签名会节省算力开销.因为链上验签是需要消耗节点算力的，而多重签名的验证机制就等同于一次签多个单签名，也就增加了算力成本的开销.

另外从第3节的实验中可以看出，BPLSM协议中多方签名、验签的时间普遍比BLS签名、验签时间快.但实验中只进行了验签部分开销的分析，并没有对链下签名部分展开比较，这是因为实验代码模拟的是参与三方同时在线的状态进行的测试.由于BPLSM协议中包含Pedersen承诺与Schnorr签名2部分，在签名同时往往需要进行2次交互，这就给签名时间的损耗带来了不可控因素，因此并没有在签名部分与BLS签名进行详细的比较.

4.2 存储开销

通过Schnorr协议进行签名，使用到了公共密钥的merkle树来进行存储.虽然在签名计算的参与方少且固定的情形里存储开销并不是很大，但是如果推广到参与方多且不固定人数的情形里，存储空间的开销就会随着参与人数增多而不断地增大.

4.3 隐私承诺

对隐私数据机密性要求高的场景中，Hash承诺不具备随机性，从而导致提供的数据隐匿性有限.对于单一隐私数据d，H(d)值是恒定的，所以利用Hash彩虹表即可推出H(d)中实际承诺的d.而Pedersen承诺具有便于业务系统在密文形式下对其处理的附加特性，在多个关联的承诺值间实行加密运算和交叉验证便会发挥很大的作用.但Pedersen承诺由于不直接提供解密功能，在互不透露的数据明文的多方协同计算中还需要结合其他功能性的密码学算法进行扩展.

5 总结与展望

本研究从多方计算的场景出发，结合区块链技术提出了一种泛用型数据隐私保护的安全多方计算协议BPLSM.该协议实现了在链上验签并做到了承诺的保证、加密值的正确性和地址的隐藏，并在链下利用Pedersen加法同态的特性实现了组合的交易承诺，结合Schnorr协议构造了可以签署不同消息的安全多方计算的方案，保证了该链下计算方案中参与方身份鉴别的零知识性和交易签名的正确性.同时，对设计的协议进行了实验仿真.证实了该隐私计算的解决方案在小范围人数固定的多方交易中，验签的时间成本会比当前的BLS签名降低约83.5%.

考虑到协议仅在实验仿真阶段，并没有将设计的BPLSM协议放入更贴近实际的多方应用场景中进行分析.在现实场景中链下签名存在诸多不可控因素，如签名方不同时在线、漏签等，因此本研究的下一步工作将会是把协议应用到具体的场景中，如跨境贸易场景，通过BPLSM协议来融合当前主流的零知识证明算法来进一步优化.

此外，BPLSM协议虽然引入随机数实现了信息论安全的最强隐蔽性，但是随着Shor算法、Grover算法等量子密码学算法的出现，在多项式时间内求解离散对数的困难问题开始变得容易[22]，协议中基于椭圆曲线的生成元G和H便不能有效抵抗量子计算的攻击.如何融入量子同态加密[23]、引入量子比特承诺[24]来设计一个后量子安全的新型多方安全计算协议应用至网络舆情治理、区块链舆情存证等方面也是接下来的研究发展方向.

贡献说明:刘峰在创意提出、区块链技术实现及论文撰写上做出了贡献，杨杰在形式化推导，核心协议的辅助实现及论文撰写上做出了贡献，李志斌(通信作者)在本文的数学推导符号及框架设计上进行了建议和指导，齐佳音(共同通信作者)从文章场景设计角度上进行了建议和指导.