软岩隧道塌方事故致灾因素耦合分析*

安亚雄，郑君长，张 翾

(1.中国路桥工程有限责任公司，北京 100008； 2.交通部公路科学研究院，北京 100073)

0 引言

在软岩隧道修建时，软岩隧道复杂的围岩条件、不准确的岩体力学参数以及随机分布的节理裂隙等原因，经常导致塌方事故发生，塌方成为建设过程中1个常见的工程灾害[1-2]。2007年5月，重庆市巫山县桃树娅隧道发生塌方事故[3]，塌方量5 000 m3；2005年3月，山西省太谷县范家岭1号隧道发生塌方事故[4]，塌方量为3 700 m3；2014年12月，福建省龙岩市新罗区厦蓉高速公路后祠隧道出口段发生塌方事故[5]，塌方量约5 000 m3。软岩隧道塌方事故不仅造成隧道结构破坏、拖延工期和经济损失，而且可能会对现场作业人员的生命安全构成威胁[6]。

在软岩隧道塌方研究中，不同学者从塌方原因、塌方预测分析等多方面开展大量研究。在塌方原因分析方面，李珏池[7]针对浅埋软岩隧道，运用离散元法分析节理角度对塌方形式的影响，得出竖向节理走向的塌方范围最大，横向节理走向最有利于围岩的稳定；Zuo等[8]分析地质构造和地下水的协同作用引起跨越断层富水软岩隧道的塌方机理；Wang等[9]认为围岩强度低和地下水的软化作用是导致强震区软岩隧道塌方的主要原因。在塌方预测分析方面，徐海清等[10]建立尖点突变理论的软岩隧道的突变失稳预测模型；Yang等[11]提出1种基于Hoek-Brown破坏准则的不同围岩遇水软化程度下软岩隧道塌陷面积估算方法。上述研究大都从单一塌方案例着手分析，鲜有学者收集不同软岩塌方案例综合分析软岩隧道塌方的致灾因素。

目前在交通管理、生态系统、机械工程、经济管理、计算机科学等多个研究领域已广泛应用耦合的概念来研究风险耦合相关性问题。Pan等[12]基于模糊熵理论和耦合度模型，建立盾构隧道施工安全风险体系的综合指标体系；张津嘉等[13]利用N-K耦合模型分析瓦斯爆炸事故各风险因素之间的耦合关系；王慧[14]运用N-K耦合模型对地铁施工过程中的“人、机、环、管”4因素对施工风险进行耦合分析。在软岩隧道塌方事故分析方面，还未引进耦合分析概念与模型，故研究致灾因素耦合作用对软岩隧道塌方事故影响具有重要的科学与工程意义。

传统方法均从识别风险源出发，通过计算风险源发生概率与损失度来评估风险危害程度。而较少从事故案例的分析与统计出发，也较少从确定性的事故致灾因素的统计中寻找多工程因素共同耦合致灾机制，从而分析事故灾害的产生机制。本文基于整理的142个软岩隧道塌方事故案例，分别对洞身段和洞口段塌方的事故原因进行分析，确定2种塌方类型下的最主要致灾因素。同时基于系统动力学和N-K耦合模型分别对多个致灾因素的耦合致灾作用进行定性和定量的分析计算，确定最主要的耦合致灾关联组合和主要影响因素。

1 软岩隧道塌方事故统计

本文统计了94个洞身段和48个洞口段塌方事故案例。根据事故案例说明，将塌方事故的致灾因素划分为地质因素、设计因素、施工因素和自然灾害因素4大类与13个小类。统计塌方事故案例的致灾原因，并且根据每个事故的特征划分诱发其事故发生的致灾因素及统计每个小类致灾因素出现频率，其结果见表1。

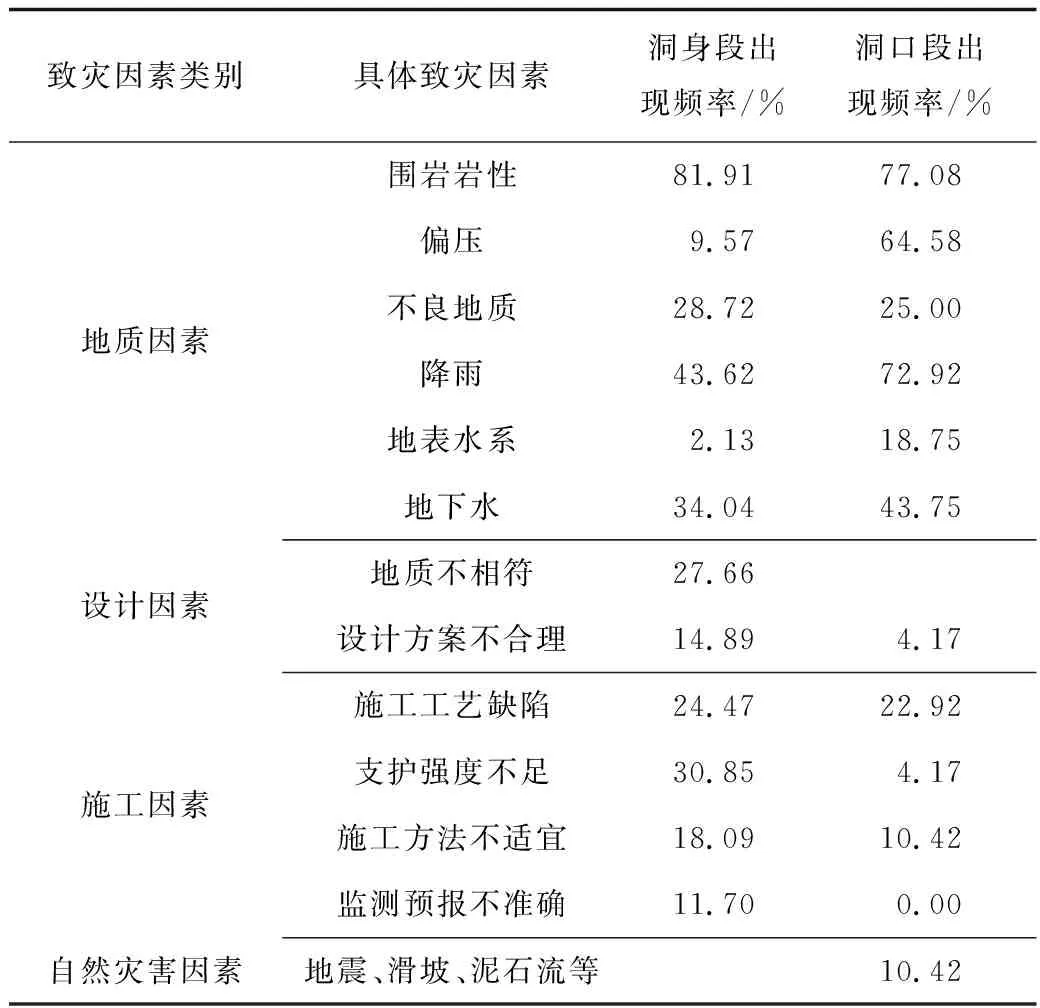
表1 隧道塌方致灾因素的出现频率Table 1 Occurrence frequencies of tunnel collapse accident-causing factors

在隧道洞身段塌方事故中，致灾因素的出现频率排序前4位的是：围岩岩性(81.91%)、降雨(43.62%)、地下水(34.04%)、支护强度不足(30.85%)。在隧道洞口段塌方事故中，致灾因素的出现频率排序前4位的是：围岩岩性(77.08%)、降雨(72.92%)、偏压(64.58%)、地下水(43.75%)。

通过比较洞身段和洞口段塌方致灾因素的出现频率可知，洞口段中致灾因素排名第4的地下水出现频率为43.75%，基本与洞身段中致灾因素出现频率排名的第2的降雨因素的43.62%持平。说明在洞口段塌方中，受降雨、地下水等致灾因素的影响远比洞身段塌方时出现频率高，在洞口段施工时更易发生塌方事故。

2 耦合过程和耦合路径

2.1 耦合类型分析

在进行耦合分析的过程中，可在出现频率较大的致灾因素基础上进行隧道塌方的耦合分析，最终确定致灾因素的耦合路径。

在洞身段和洞口段塌方的耦合分析中，分别对4个主要致灾因素进行排列组合，确定其之间的耦合关系，计算可知软岩隧道洞身段和洞口段塌方的2因素耦合情况共为6种，3因素和4因素耦合情况共为5种。

2.2 耦合路径分析

工程事故的发生是致灾因素的耦合诱发所导致的，需要通过致灾因素之间的耦合路径来实现，因此本文利用系统动力学分析因素之间的耦合路径。在因果与相互关系图中，因果关系链包括正因果链和负因果链，可以描述因素间的作用原理。当因素A对B有促进作用时用正因果链来表示，本文耦合路径的因果关系均为正因果关系。

洞身段耦合分析中3因素和4因素的耦合路径为5种，耦合路径如图1所示。

1)围岩岩性-降雨-地下水3因素耦合

易塌方地层的围岩整体强度较低，完整性较差，在隧道开挖过程中极易发生塌方事故。地下水的渗水压力、软化作用伴随降雨对节理的冲刷致使岩体中节理的黏聚力降低，围岩的强度将进一步下降，围岩的岩性出现劣化，在实际工程中极易发生塌方事故。

2)围岩岩性-降雨-支护强度不足3因素耦合

在隧道洞身段塌方的过程中，围岩的岩性相对较差，在隧道修建过程中拱顶极易发生塌方事故。而且在持续性的强降雨过程中，降雨在拱顶部位的裂隙发生汇集，对拱顶部位的围岩造成软化膨胀作用，进一步降低围岩自身的承载能力，支护强度形成的及时性得不到保证。降雨对围岩和支护的影响范围进一步增加，最终导致隧道的塌方。

3)围岩岩性-地下水-支护强度不足3因素耦合

在隧道开挖过程中，对围岩扰动会导致围岩出现松动圈，围岩完整性大幅降低，围岩的自身承载能力也会下降，同时在地下水作用下会出现支护强度不足的现象，继而发生隧道的塌方事故。

4)降雨-地下水-支护强度不足3因素耦合

由于地下水和降雨均能降低支护结构混凝土的强度，在支护强度不能按期形成、支护的及时性得不到保证的情况下，隧道出现塌方时塌方范围将逐步增大，最终导致大范围的塌方。

5)围岩岩性-降雨-地下水-支护强度不足4因素耦合

地层围岩岩性较差，围岩强度相对较低时，易受水环境的影响，在该地层开挖隧道极易出现塌方事故。此外，降雨容易导致支护强度不足，围岩与支护的共同承载能力并不能达到初始设计要求，围岩压力与水压力的共同作用使得隧道所处的应力环境难以形成稳定的隧道结构。在隧道荷载增加且隧道与支护共同承载能力下降的不利因素叠加过程中，塌方范围进一步增大直至隧道形成稳定拱为止。

同理，洞口段耦合分析中3因素和4因素的耦合路径为5种，耦合路径如图2所示。

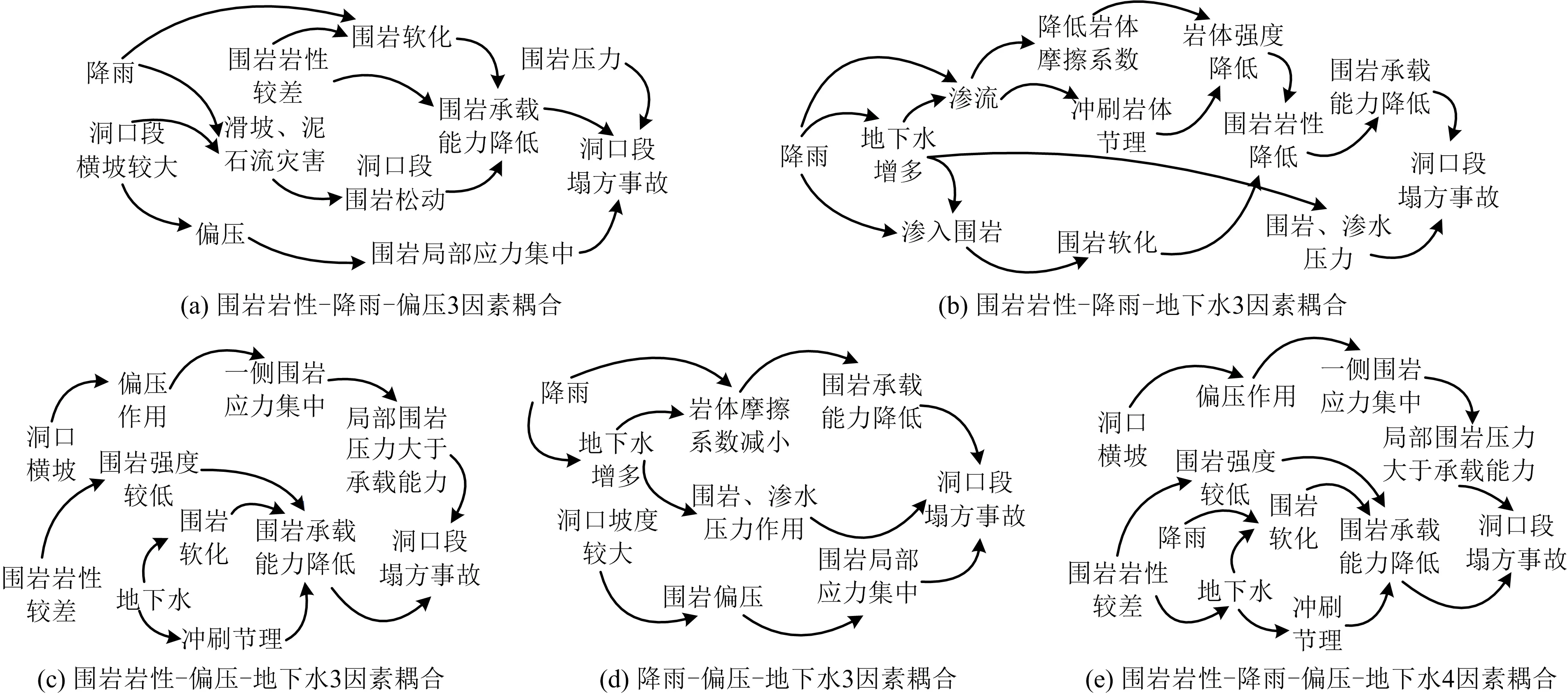
图2 洞口段塌方事故的3因素和4因素耦合路径Fig.2 Three-factor and four-factor coupling path diagrams of collapse accident at entrance section

3 基于N-K模型的耦合模型

N-K模型由Kaufman于1995年提出的，适用于解决复杂系统网络的问题。N-K模型包括组成系统的元件数目(N)和网络中相互关联的元件数目(K)，K值的大小决定系统的适应度。对于1个复杂网络，如果网络中含有N个元素，每个元素有n个状态，则所有可能的组合方式就有nN种。K值最小为0，最大为N-1。本文采用N-K模型作为描述与测度致灾因素之间耦合关系的数学模型。

塌方隧道耦合分析过程需要对塌方事故的4个致灾因素分别计算2,3,4致灾因素耦合关联值，以耦合关联值T来代表这种耦合后新状态的危险程度，当T值越大，则证明该耦合组合导致事故出现的可能性越大，该耦合组合越危险。

3.1 2致灾因素耦合值计算

2致灾因素耦合有6种模式。围岩岩性、地下水、降雨、支护强度不足4个致灾因素分别用1,2,3,4表示，2致灾因素的耦合关联值T表示见表2。公式(1)～(6)为2致灾因素耦合值计算公式。

表2 2致灾因素的耦合关联值表示Table 2 Representation of coupling value for two accident-causing factors

(1)

(2)

(3)

(4)

(5)

(6)

式中:p为各种组合的耦合概率;h，i，j，k分别为围岩岩性、地下水、降水、支护强度因素状态值；H,I,J,K分别表示h,i,j,k的取值范围。此处h,i,j,k的状态值由0和1来表示，“1”代表某一致灾因素出现，“0”代表某一致灾因素未出现，“.”表示某一致灾因素发生状态不确定，统计时计算未发生和已发生的概率总和。

3.2 3致灾因素耦合值计算

用T123表示围岩岩性、地下水、降雨因素耦合值；T124表示围岩岩性、地下水、支护强度不足因素耦合值；T134表示围岩岩性、降雨、支护强度不足因素耦合风险值；T234表示地下水、降雨、支护强度不足因素耦合值，3因素耦合值的计算如式(7)～(10)所示：

(7)

(8)

(9)

(10)

3.3 4致灾因素耦合值计算

设围岩岩性、地下水、降雨、支护强度不足耦合值为T1234，4因素耦合值的计算如式(11)所示：

(11)

4 致灾因素耦合计算

4.1 洞身段致灾因素耦合关联值计算

根据94个塌方事故案例的统计结果，采用N-K模型的耦合模型计算隧道塌方事故的耦合关系。设I1，I2，I3分别表示单致灾因素、2致灾因素、3致灾因素的风险耦合形式，塌方事故致灾因素耦合发生频率见表3。表3中1代表某一致灾因素出现，0代表某一致灾因素未出现，如P1100表示只有因素1和2同时发生的事故占总事故的概率，共94个案例。

表3 隧道洞身段塌方事故风险耦合发生频率Table 3 Occurrence frequencies of risk coupling for collapse accident at tunnel body section

4.1.1 交互信息概率计算

1)单因素确定的交互信息概率(“.”表示风险发生状态不确定，计算未发生和发生的概率总和)

P0...=P0000+P0001+P0100+P0010+P0101+P0011+P0110+P0111=0.181,同理可得其他的单因素确定的交互信息概率见表4。

表4 单因素确定的交互信息概率Table 4 Probabilities of interactive information determined by single factor

2)2因素确定的交互信息概率

P00..=P0000+P0001+P0010+P0011=0.138,同理可得其他的2因素确定的交互信息概率见表5。

表5 2因素确定的交互信息概率Table 5 Probabilities of interactive information determined by two factors

3)3因素确定的交互信息概率

P000.=P0001+P0000=0.085,同理可得其他的3因素确定的交互信息概率见表6。

表6 3因素确定的交互信息概率Table 6 Probabilities of interactive information determined by three factors

4.1.2 耦合关联值计算

由公式(1)～(6)计算隧道洞身段塌方事故的2因素耦合关联值大小分别为：T12=10.00%,T13=1.28%,T14=0.06%,T23=4.74%,T24=6.30%,T34=0.78%。

由公式(7)～(10)计算，隧道洞身段塌方事故的3因素耦合关联值大小分别为：T123=17.79%,T124=2.45%,T134=16.97%,T234=12.61%。

根据公式(11)计算，隧道洞身段塌方事故的4因素耦合关联值大小为T1234=27.02%。

4.1.3 风险排序

根据洞身段耦合风险的计算结果，洞身段塌方各耦合风险值大小如图3所示，即T1234≥T123≥T134≥T234≥T12≥T24≥T23≥T124≥T13≥T34≥T14。由排序可知，耦合关联值的大小并不完全取决于单一致灾因素出现频率大小，统计概率较小的3因素的耦合关联值可能比概率较大的3因素耦合关联值更大。而且在耦合关联值排序中，2因素组合的耦合关联值(T12,T24,T23)甚至大于部分3因素组合的耦合关联值(T124)，说明耦合过程中会出现随机性，耦合作用并非单一因素的叠加。

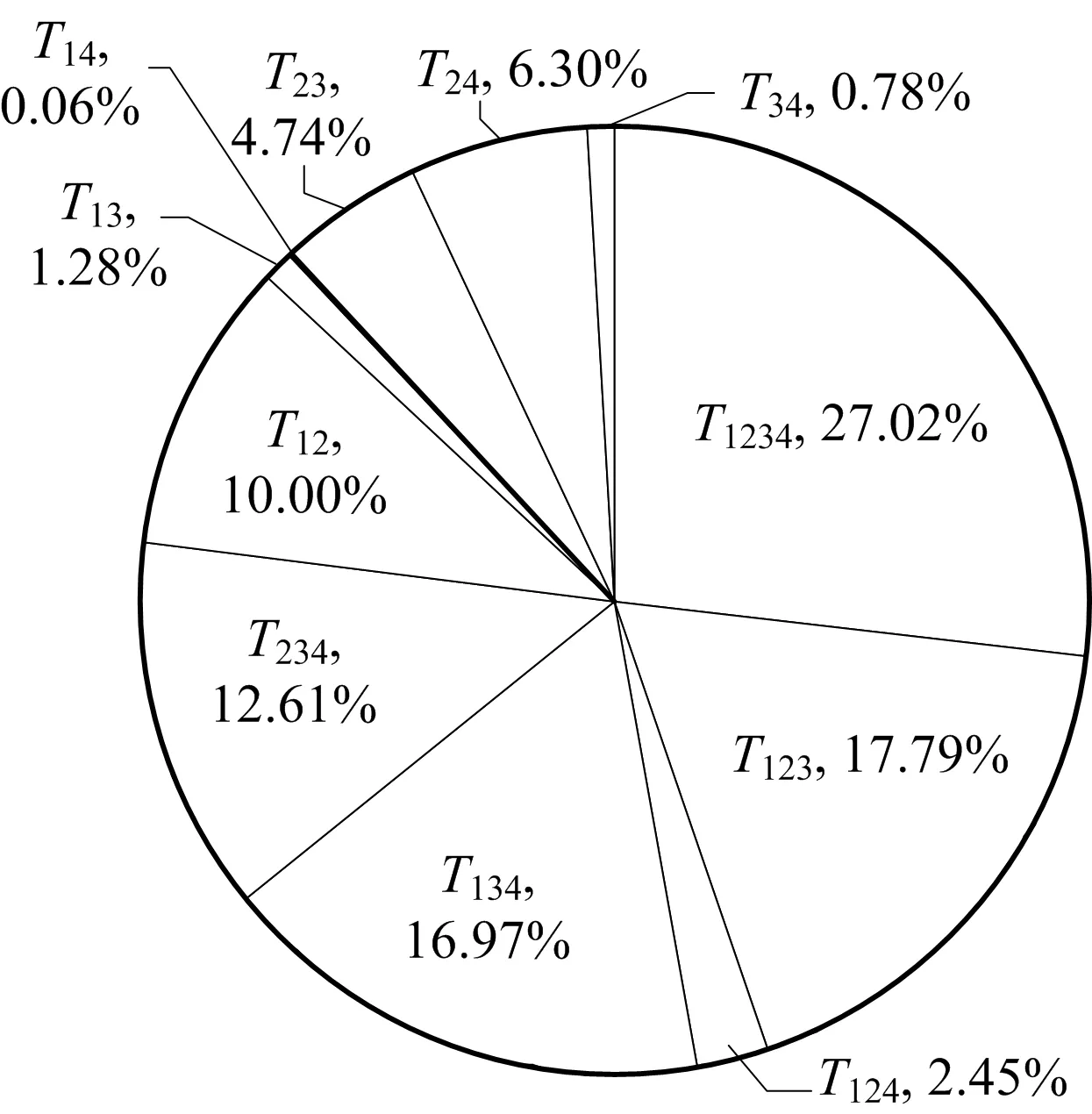
图3 洞身段塌方各耦合风险值大小Fig.3 Coupling risk values of collapse at body section

为较好地控制耦合关联，应在设计之初尽量避开围岩岩性较差、地下水环境较复杂的地段；并在施工过程中及时施加初期支护，做好地下水的防排截堵和地表水的导排，从而降低对工程影响。

4.2 洞口段塌方耦合关联值计算

采用N-K耦合模型对48个隧道洞口段塌方事故案例进行耦合关联值计算。洞口段4个主要致灾因素分别为围岩岩性、降雨、偏压、地下水因素。洞口段塌方事故致灾因素耦合发生频率见表7。

表7 隧道洞口段塌方事故风险耦合发生频率Table 7 Occurrence frequencies of risk coupling for collapse accident at tunnel entrance section

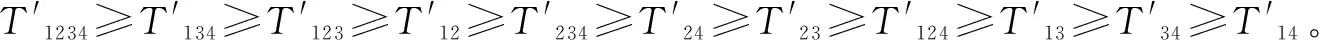
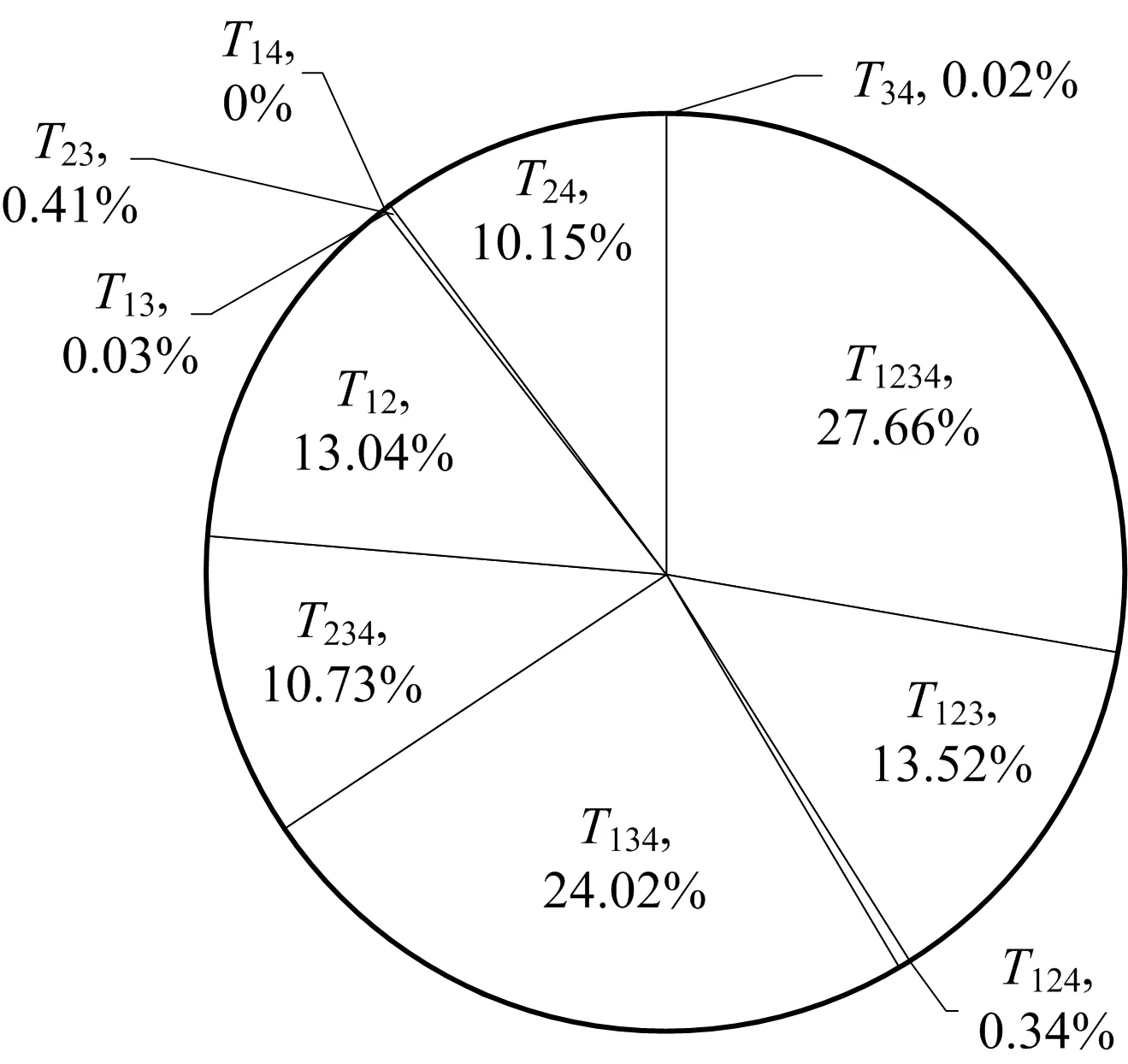
图4 洞口段塌方各耦合风险值大小Fig.4 Coupling risk values of collapse at entrance section

5 结论

1)隧道洞身段塌方事故的主要4个致灾因素出现频率，围岩岩性为81.91%、降雨为43.62%、地下水为34.04%、支护强度不足为30.85%；隧道洞口段塌方事故的主要4个致灾因素出现频率，围岩岩性为77.08%、降雨为72.92%、偏压为64.58%、地下水为43.75%。

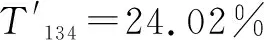
3)围岩塌方是软岩隧道施工中常见的重大事故类型，事故原因多元且互相耦合。该耦合关系的确定是基于大量的工程案例，而非专家的主观判断，提高研究结果可信度和客观性。