基于非参数相关系数的心肌病自动诊断

林卓琛，张晋昕

前言

2015年，由心血管疾病所致的死亡人数占全球死亡人数的31%。2016年，世界卫生组织将其确定为全球居民主要死因，2001年至2015年间每年约有1 750 万人死于该病［1］。这个数字随着世界人口的年龄增长，在2030年预计将增加到2 220 万［2］。调查显示，2010年由心血管疾病引起的全球直接医疗费用约为8 630 亿美元，并且在2030年累计将达到20 万亿美元［3］。而在中国，心脏病的患病率和死亡率一直处于不断上升状态，及早发现心肌病在内的心脏疾病，显得尤为重要［4］。

临床医生通常使用12 导联心电图来评估各种心血管疾病的发病风险，心电图机是一种将电极放在皮肤上的工具，用于收集一段时间内心脏电活动的信息［5］。然而，人工研判这些心电图是单调、耗时的，对于那些关键的、同时也是细微的诊断细节，单纯通过人工评阅可能会有遗漏，甚至导致心电图研判的错误［6］。因此，为了克服人工评估的局限性，越来越多的研究者开发了相应的计算机辅助自动诊断技术。

当前使用心电图数据进行自动分类的关键在于信号特征的提取。有的研究者直接对原始ECG 数据进行特征提取，也有的研究者首先进行小波分析等处理得到小波系数后再进行分析，虽然小波分析存在小波基选择等问题，其多分辨率分析的特点使其在时频域上有效提取信号的局部特征，因此仍是当前研究者选择的主要心电数据处理方法。

人们对于心电数据特征的提取主要是以统计特征为主，主要包含描述波形信息的特征如偏度、峰度［7］，描述能量信息的方差［8］，描述导联信息量的熵［9］等。除统计特征外，有研究者尝试使用多项式拟合系数［10］、分型系数［9,11］等作为信号的特征。然而，人们对特征的研究多集中于单个导联提取的特征，对于导联间的相关性开展深入挖掘的力度不足。Maharaj 等［12］曾在2014年研究了小波分析系数的导联间相似性对心肌梗死的影响，但是没有考虑到小波系数在各个分解层级中可能正态性欠佳，也没有考虑到导联的系数间不是线性关系。本研究提出一种基于非参数的相关系数特征，稳健地刻画了导联间的相关性，对分解后系数不作正态性假设。本研究的分析流程图见图1，本研究采用Matlab2018b 进行数据分析。

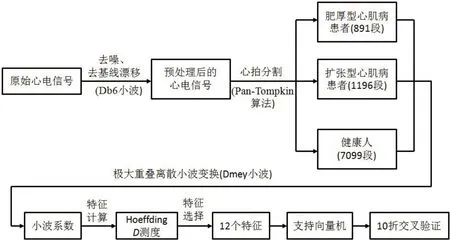
图1 本研究分析流程图Fig.1 Flow diagram of research design

1 特征提取

1.1 数据来源

德国国家计量署的PTB数据库来自柏林本杰明富兰克林（Benjamin Franklin）医院心脏内科，常用于心脏疾病相关算法的研究，是本研究的合适选择。该数据库包含148名心肌梗死患者、18名冠心病及心衰患者、15名束支传导阻滞患者、14名心率失常患者、52名健康人以及21名其余心脏相关疾病患者。每个记录采用并列储存方式，包含15列，分别为标准12导联（I,II,III,avR,avL,avF,V1,V2,V3,V4,V5,V6）和3富兰克林导联（vx,vy,vz），值域范围为-1 000～3 000 mV，表示该时间点下心电信号的强度。每个记录时长约2 min（120 000个采样点/行），采样率为1 000 Hz，分辨率为16 bit（±16.384 mV），储存格式为Format 16。本研究使用其中的标准12导联信号进行分析。本文旨在考察鉴别诊断方法的诊断能力，与其他报道进行对比。所以，也按照已有报道的做法［13-14］，纳入数据库中所有的健康人、肥厚型心肌病患者和扩张型心肌病患者。纳入患者以临床医生的诊断结果为准划分组别，排除掉合并其他心脏系统疾病的患者，最后选择了来自PTB数据库的52名健康人、7名肥厚型心肌病患者和9名扩张型心肌病患者进行分析研究。

1.2 数据预处理与心拍分割

为了消除心电信号带有的各类型噪声干扰（工频干扰、基线漂移和高频干扰等）［15］，本研究使用Daubechies 6（db6）小波基函数对心电信号进行去噪和消除基线漂移［16］。与主流的分析方法相一致，本研究用0.351～125.000 Hz 带通滤波进行过滤，随后使用5 到11 层的细节系数重构信号。预处理后的信号高频噪声被过滤，局部变得光滑，信号整体处于同一水平。

去噪后的整体信号需要根据独立的心动周期分割为单独的心电片段，本研究使用Pan-Tompkin 算法进行R 峰的识别来达到心拍分割的目的［17］。Pan-Tompkin 算法是一个稳健的R 峰识别算法，计算简单，易于实现。将R 峰前的255 个采样点、R 峰后的256 个采样点以及R 峰本身作为一个单独的片段进行后续分析（共512个采样点），最终每个人的心电信号将被分割为80～160个完整的心拍信号。为了确保片段的长度符合标准，我们删除了每个人的第一个片段和最后一个片段，使得所有的片段具有相同的长度。最终从7名肥厚型心肌病患者中提取片段891段，9名扩张型心肌病患者中提取片段1 196段，52名健康人中提取片段7 099段。

1.3 小波分析

获取心电图片段后，对该片段512 个采样点进行归一化处理，使其总方差等于1。处理后不同碎片之间总能量的差异被消除，有利于后续挖掘有意义的特征。我们使用极大重叠离散小波变换（MODWT）来分解原始信号［18］。MODWT 是对离散小波变换的一种改进，它不使用下采样过程，因此所有尺度上的小波系数都具有与原始时间序列长度相等的长度，在处理相关问题上MODWT 的这个特性会有一定的优势。每个片段经过以dmey 为小波基的MODWT后被分解为7个层级［19］。我们只使用了5到7层的细节系数以及第7 层的逼近系数。这4 个系数序列包含0.351～62.500 Hz 频带范围，涵盖了原始信号几乎所有的信息。每一个小波系数序列包含512 个值。关于ECG 经过MODWT 产生4 个小波系数序列的一个示例见图2。

图2 基于dmey小波的原始信号和分解信号Fig.2 Raw signal and decomposed signals based on dmey wavelet

1.4 非参数相关系数的计算

经过小波分解后，每个导联可计算出4个小波系数。对于同一种小波系数，我们计算12 个导联两两间的非参数相关系数。每一种小波系数计算出66个特征，共计264个特征。HoeffdingD测度的直观思想是通过计算零假设（两变量独立）下边际分布乘积与经验二元分布之间的距离来检验数据集的独立性［20］。这两个分布之间的差异越大，D就越大，导联间相关性就越大。HoeffdingD测度有助于识别非线性、非单调关联。其计算公式如下：

其中，记原始信号X 在MODWT 分解后的第j条系数序列为Wx,j,·，原始信号Y 在MODWT 分解后的第j条系数序列为Wy,j,·，本研究每个导联使用4 条系数序列。Ri是Wx,j,i在系数序列Wx,j,·由小到大排序后得到的秩。而Si是Wy,j,i在系数序列Wy,j,·由小到大排序后得到的秩。将序列Wx,j,·与Wy,j,·结成的n对点对(Wx,j,t,Wy,j,t)(t= 1,…,n)，Qi是点对中的两者同时小于(Wx,j,t,Wy,j,t)的点对个数。

通过计算、整理，最终每个心拍片段计算得到264 个HoeffdingD测度，组成9 186×264 的矩阵。部分计算结果见图3。其中结局标签的含义为1：健康人，2：扩张型心肌病，3：肥厚型心肌病；受试者id 为每个受试者的编号，片段id 为同一个受试者内心拍片段的编号；紧接的264 列为HoeffdingD测度，编码形式为x_y_z，其中x 的含义为5：第5 层细节系数，6：第6层细节系数，7：第7层细节系数，8：第7层的逼近系数；y 与z 表示第y 导联与第z 导联，第1 至12 导联依次对应导联I,II,III,avR,avL,avF,V1,V2,V3,V4,V5,V6。

图3 Hoeffding D测度计算结果（部分）Fig.3 Calculated results of Hoeffding D measure(part of contents)

1.5 特征选择

得到的264个特征中含有对疾病预测有价值的特征，需要通过变量选择的方式挑选出来。对于每个特征，本研究通过方差分析（ANOVA）计算其关于3个结局的F值。F值越大，说明特征越重要。使用10折交叉验证分别计算F阈值为1 100～4 900时的总准确率均值以及标准差，具体见图4。随着F值增大，在抵达辅助线（纵向虚线F=3 600处）之前，被保留下来特征数在减少，总正确率并未减低；当F值进一步增大，越过辅助线后，总准确率均值开始下降，且标准差开始增大。可见3 600是比较合适的F阈值，此处对应的预测正确率高，且稳健。

根据变量的F值对变量进行排序，挑选出较重要的特征。选择F值在3 600 以上的特征，共挑选出12个特征，特征的情况见表1，Hr3,65表示展开的第5层第3 导联和第6 导联的HoeffdingD测度，其余符号按相同规则标记。

2 建模与结果分析

2.1 建模与评价介绍

分类任务涉及训练集和测试集的划分，通过将训练集输入到支持向量机中建立预测模型，并使用测试集评价模型的优劣。本研究使用10折交叉验证评价模型效果，通过随机分组，将计算得到的9 186个心拍片段平均分成10 份，每次取出其中1 份作为测试集，余下9份合并在一起作为训练集。使用训练集进行建模后，对预测集进行预测，得到1 次预测结果。这个过程重复10次，计算出其均数和标准差，可对模型预测能力做出准确而稳健的评价。

表1 前12个重要特征在3组间的情况（± s）Tab.1 The result of the first 12 important features among 3 groups(Mean±SD)

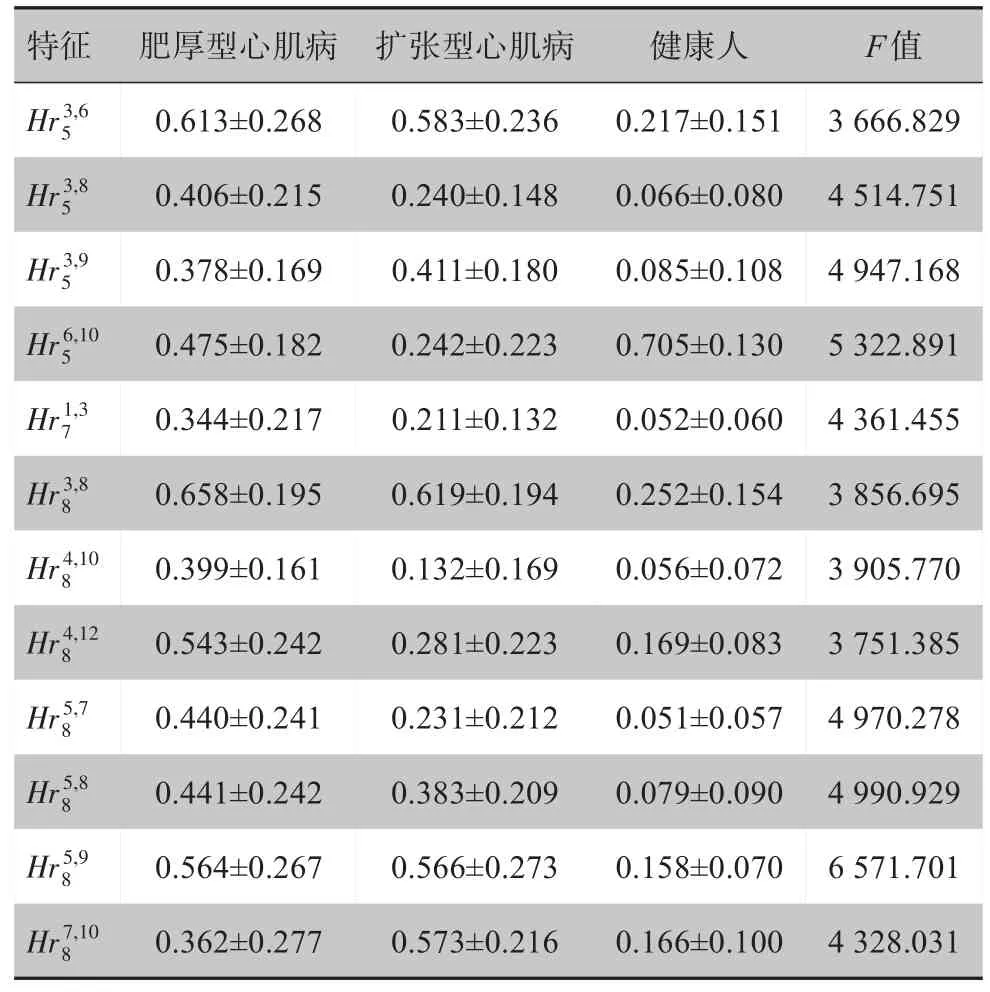
表1 前12个重要特征在3组间的情况（± s）Tab.1 The result of the first 12 important features among 3 groups(Mean±SD)

特征Hr3,6 5 Hr3,8 5 Hr3,9 5 Hr6,10 5 Hr1,3 7 Hr3,8 8 Hr4,10 8 Hr4,12 8 Hr5,7 8 Hr5,8 8 Hr5,9 8 Hr7,10 8肥厚型心肌病0.613±0.268 0.406±0.215 0.378±0.169 0.475±0.182 0.344±0.217 0.658±0.195 0.399±0.161 0.543±0.242 0.440±0.241 0.441±0.242 0.564±0.267 0.362±0.277扩张型心肌病0.583±0.236 0.240±0.148 0.411±0.180 0.242±0.223 0.211±0.132 0.619±0.194 0.132±0.169 0.281±0.223 0.231±0.212 0.383±0.209 0.566±0.273 0.573±0.216健康人0.217±0.151 0.066±0.080 0.085±0.108 0.705±0.130 0.052±0.060 0.252±0.154 0.056±0.072 0.169±0.083 0.051±0.057 0.079±0.090 0.158±0.070 0.166±0.100 F值3 666.829 4 514.751 4 947.168 5 322.891 4 361.455 3 856.695 3 905.770 3 751.385 4 970.278 4 990.929 6 571.701 4 328.031

2.2 支持向量机

支持向量机是定义在特征空间上使得类间间隔最大化的线性分类器，通过引入选定的核函数，将输入空间的特征映射到一个高维的特征向量空间中，并在该空间中构造最优分类平面，实现健康信号与两种心肌病的分类。本研究采用径向基函数作为核函数，对于需要选定的超参数c和γ，使用网格搜索法得到理想值，c等于2.83，γ等于4。

2.3 分类结果

以真实疾病结局为横行，预测疾病结局为纵列，对每个人预测情况进行计数，统计出混淆矩阵，结果见表2。采用总体准确率（Acc）以及各类结局的灵敏度（SenHC,SenDCM,SenHCM）和特异度（SpecHC,SpecDCM,SpecHCM）评价模型结果。指标的计算公式如下：

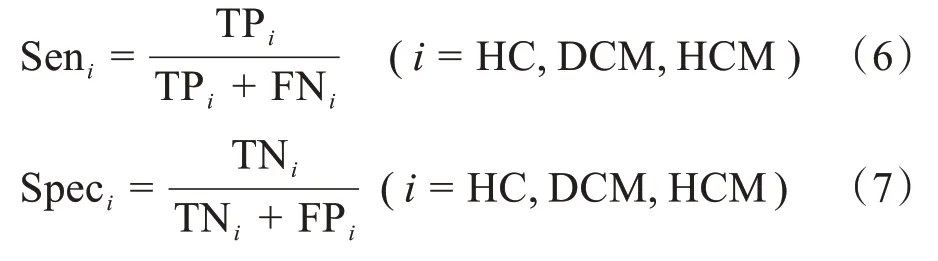
其中，HC、DCM、HCM 分别代表健康人、扩张型心肌病以及肥厚型心肌病。TPi表示属于第i类结局且被正确预测的心拍个数；FPi表示不属于第i类结局但被错误地预测为第i类结局的心拍个数；TNi表示不属于第i类结局的心拍且被预测为非第i类结局的心拍个数；FNi表示属于第i类结局的心拍但没有被预测为第i类结局的心拍个数。总准确率公式中分子为3类结局预测正确的心拍个数，分母为总心拍个数。灵敏度公式中分子为第i类正确预测的心拍个数，分母为真是患有第i类结局疾病的心拍个数。特异度公式中分子为不属于第i类结局的心拍且被预测为非第i类结局的心拍个数，分母为不属于第i类的心拍个数。由于采用10 折交叉验证，结果得到了10 个准确率、灵敏度和特异度，分别计算其均数与标准差，结果见表3。

表2 分类结果的混淆矩阵Tab.2 Confusion matrix of classification results

表3 模型分类的评价指标（%）Tab.3 Evaluation measurements to the classifications(%)

当前对于心肌病自动诊断的研究仍较少，且多为健康人与单个心肌疾病之间的鉴别诊断。近几年对心肌病的研究结果见表4，由表可以看出，本研究提出的特征计算简单、方便，同时对两种心肌病进行预测且总准确率均高于同类研究。

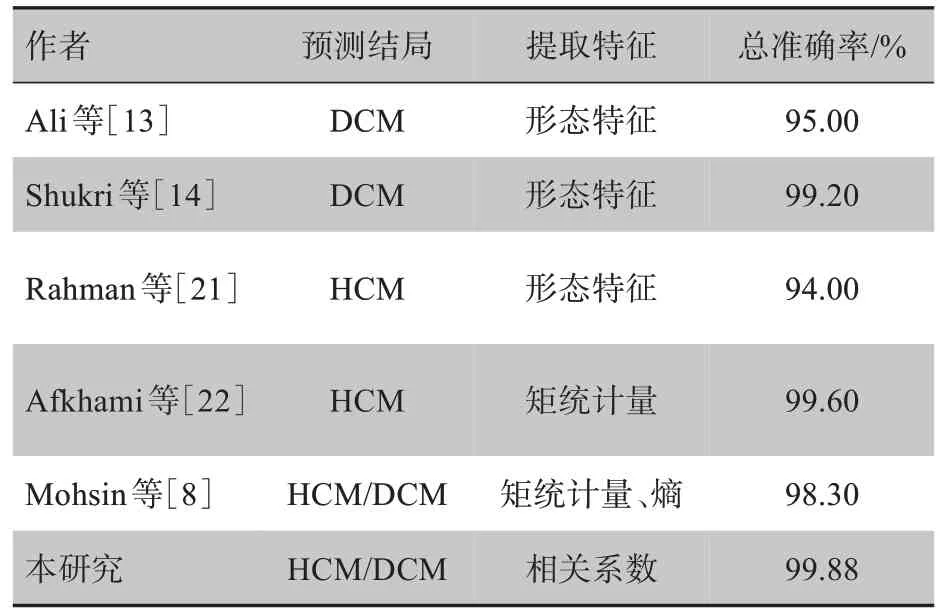
表4 与近期其他文献结果比较Tab.4 Comparison with the results from other recent studies

3 结论

基于心电图导联间的相关性，本研究提出使用HoeffdingD测度对两种心肌病进行自动诊断的算法。首先使用MODWT 对预处理后的心电图信号进行分解，随后计算4 层12 个导联间小波系数的HoeffdingD测度，通过F检验提取最重要的12 个特征，使用支持向量机分类器实现对两种心肌病与健康心拍的自动分类。本文最终识别正确率达到99.88%，优于同类型研究，可用于辅助临床心肌病的预测与诊断。

本研究在当前阶段使用国际公开数据库进行建模分析，尚未在当地医院进行数据收集以及相关的模型检验。为结合临床的实际应用需求，本研究未来计划将与医疗机构合作，结合中国人病例数据分析两者筛选所得特征的一致程度，进一步分析模型的泛化能力与实际应用效果。